Erklärung zur Chi²

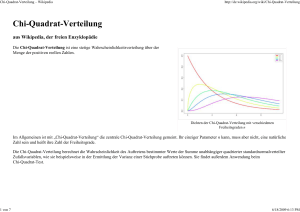
Chi2-Verteilung
Gegeben sind drei normalverteilte, paarweise stochastisch unabhängige Zufallsvariablen X1,
X2 und X3 mit den Erwartungswerten µ1, µ2 µ3 und den Varianzen σ1², σ2²,σ3². Wir
standardisieren diese Variablen und erhalten drei standardnormalverteilte Zufallsvariablen Z1,
Z2 und Z3,
Nun werden die standardnormalverteilten Zufallsvariablen quadriert und aufsummiert. Wir
erhalten eine neue Zufallsvariable
Y ist χ2-verteilt mit 3 Freiheitsgraden.
Dichtefunktion der χ2-Verteilung mit ausgewählten Freiheitsgraden
Es gilt: Die Summe von m quadrierten, stochastisch unabhängigen, standardnormalverteilten
Zufallsvariablen ist χ²-verteilt mit n Freiheitsgraden (df = n).
Man sieht anhand der Grafik, dass sich die Dichtefunktion mit wachsenden Freiheitsgraden
einer symmetrischen Kurve - der Normalverteilungskurve - nähert. Wenn die χ²-Verteilung
eine große Anzahl an Freiheitsgraden besitzt, nähert sie sich der Normalverteilung an:
Die Wahrscheinlichkeit der χ²-Verteilung wird bezeichnet als P(Y ≤ a) = fY(a|n). Das pQuantil ist χ²(p,n).
Die Verteilungsfunktion der χ2-Verteilung kann nicht analytisch ermittelt werden.
Numerische Berechnungen können beispielsweise aus Tabellenwerken, etwa Tabelle der χ²Verteilung ersehen werden. Da Y für jeden Freiheitsgrad eine eigene Verteilung besitzt, sind
in kleineren Tabellen nur Quantile nach Freiheitsgraden und ausgewählten
Wahrscheinlichkeiten aufgeführt. Z.B. ist χ²(0,95;3) = 7,81 für das 95%-Quantil (Spalte) der
χ²-Verteilung mit 3 Freiheitsgraden (Zeile). Umgekehrt gilt: die Wahrscheinlichkeit P(y ≤
7,81) = 0,95.