und t−Verteilung

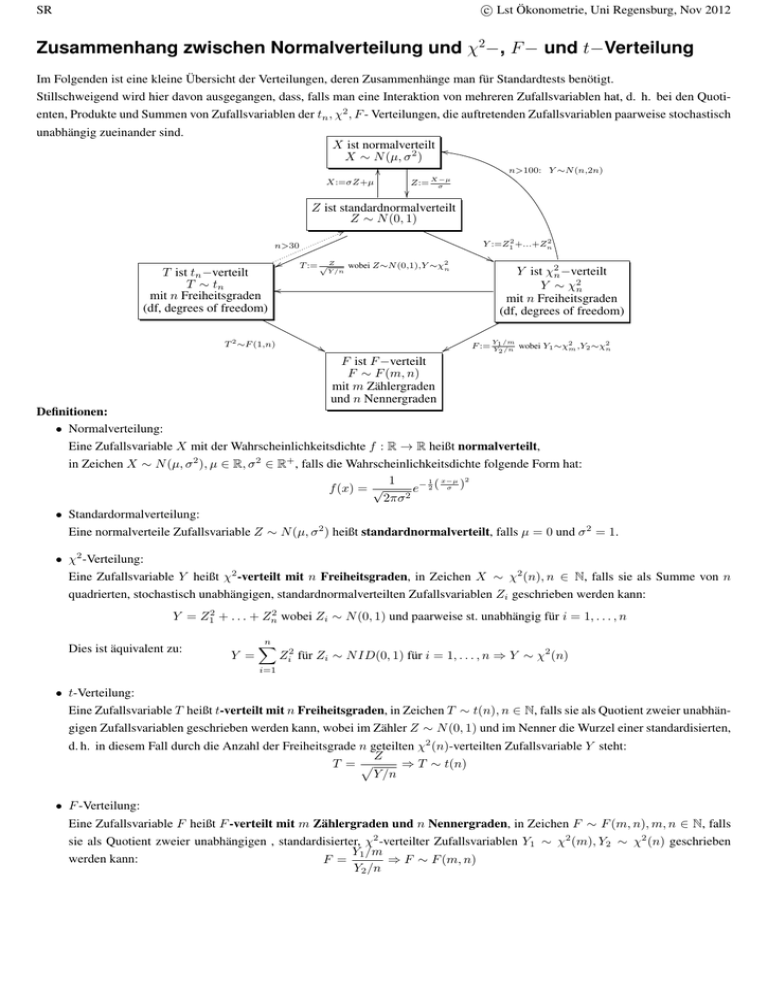
c Lst Ökonometrie, Uni Regensburg, Nov 2012
SR
Zusammenhang zwischen Normalverteilung und χ2 −, F − und t−Verteilung
Im Folgenden ist eine kleine Übersicht der Verteilungen, deren Zusammenhänge man für Standardtests benötigt.
Stillschweigend wird hier davon ausgegangen, dass, falls man eine Interaktion von mehreren Zufallsvariablen hat, d. h. bei den Quotienten, Produkte und Summen von Zufallsvariablen der tn , χ2 , F - Verteilungen, die auftretenden Zufallsvariablen paarweise stochastisch
unabhängig zueinander sind.
X ist normalverteilt m
X ∼ N (µ, σ 2 )
O
n>100: Y ∼N (n,2n)
X:=σZ+µ
Z:= X−µ
σ
Z ist standardnormalverteilt
Z ∼ N (0, 1)
7
2
Y :=Z12 +...+Zn
n>30
T ist tn −verteilt
T ∼ tn
o
mit n Freiheitsgraden
(df, degrees of freedom)
w
T 2 ∼F (1,n)
T := √ Z
Y /n
wobei Z∼N (0,1),Y ∼χ2n
&
x
'
Y ist χ2n −verteilt
Y ∼ χ2n
mit n Freiheitsgraden
(df, degrees of freedom)
Y /m
F := Y1 /n wobei Y1 ∼χ2m ,Y2 ∼χ2n
2
F ist F −verteilt
F ∼ F (m, n)
mit m Zählergraden
und n Nennergraden
Definitionen:
• Normalverteilung:
Eine Zufallsvariable X mit der Wahrscheinlichkeitsdichte f : R → R heißt normalverteilt,
in Zeichen X ∼ N (µ, σ 2 ), µ ∈ R, σ 2 ∈ R+ , falls die Wahrscheinlichkeitsdichte folgende Form hat:
1 x−µ 2
1
f (x) = √
e− 2 ( σ )
2
2πσ
• Standardormalverteilung:
Eine normalverteile Zufallsvariable Z ∼ N (µ, σ 2 ) heißt standardnormalverteilt, falls µ = 0 und σ 2 = 1.
• χ2 -Verteilung:
Eine Zufallsvariable Y heißt χ2 -verteilt mit n Freiheitsgraden, in Zeichen X ∼ χ2 (n), n ∈ N, falls sie als Summe von n
quadrierten, stochastisch unabhängigen, standardnormalverteilten Zufallsvariablen Zi geschrieben werden kann:
Y = Z12 + . . . + Zn2 wobei Zi ∼ N (0, 1) und paarweise st. unabhängig für i = 1, . . . , n
Dies ist äquivalent zu:
Y =
n
X
Zi2 für Zi ∼ N ID(0, 1) für i = 1, . . . , n ⇒ Y ∼ χ2 (n)
i=1
• t-Verteilung:
Eine Zufallsvariable T heißt t-verteilt mit n Freiheitsgraden, in Zeichen T ∼ t(n), n ∈ N, falls sie als Quotient zweier unabhängigen Zufallsvariablen geschrieben werden kann, wobei im Zähler Z ∼ N (0, 1) und im Nenner die Wurzel einer standardisierten,
d. h. in diesem Fall durch die Anzahl der Freiheitsgrade n geteilten χ2 (n)-verteilten Zufallsvariable Y steht:
Z
⇒ T ∼ t(n)
T =p
Y /n
• F -Verteilung:
Eine Zufallsvariable F heißt F -verteilt mit m Zählergraden und n Nennergraden, in Zeichen F ∼ F (m, n), m, n ∈ N, falls
sie als Quotient zweier unabhängigen , standardisierter, χ2 -verteilter Zufallsvariablen Y1 ∼ χ2 (m), Y2 ∼ χ2 (n) geschrieben
Y1 /m
werden kann:
F =
⇒ F ∼ F (m, n)
Y2 /n