zum Praktikum - Physik in Jena

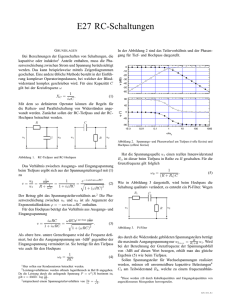
27.05.08
Messtechnik-Praktikum
Aktive Filterschaltungen - Filter II
Silvio Fuchs & Simon Stützer
1 Augabenstellung
1.
a) Bauen Sie einen aktiven Tief- oder Hochpass entsprechend Abbildung 1 bzw. 2 auf.
b) Bestimmen Sie den Frequenzverlauf der Spannungsverstärkung bei sinusförmiger Anregung. Stellen Sie diesen grafisch dar. Bestimmen Sie die Grenzfrequenz der Schaltung.
c) In welchem Teil des Frequenzverlaufes findet man ein Integrationsverhalten bzw. ein Differentiationsverhalten? Testen Sie dies mit einer rechteckförmigen Anregung als Eingangsspannung.
Beobachten Sie UE und UA als Funktion der Frequenz. Nehmen Sie für den Fall Integrationsbzw. Differentiationsverhalten die Ausgangsspannung als Funktion der Zeit auf. In welcher Phasenlage zueinander befinden sich in diesem Fall das Eingangs- und das Ausgangssignal?
2.
a) Bauen Sie die Schaltung eines selektiven Wechselspannungsverstärkers nach Abbildung 3 auf.
b) Bestimmen Sie den Frequenzverlauf der Spannungsverstärkung bei sinusörmiger Anregung. Verwenden Sie für die Messungen die Röhrenvoltmeter und kontrollieren Sie das Ausgangssignal mit
dem Elektronenstrahloszillographen. Stellen Sie den Frequenzverlauf grafisch dar (geeignete Achseneinteilung beachten).
c) Bestimmen Sie möglichst genau die Resonanzfrequenz und die Bandbreite des Selektivverstärkers.
Stellen Sie dabei die Ausgangsspannung so ein, dass auch im Resonanzfall das Ausgangssignal
nicht verzerrt wird. Vergleichen Sie die experimentell bestimmte Bandbreite mit dem theoretisch
erwarteten Wert.
1
2 Grundlagen
Im Versuch 2 lernten wir einen passiven Tiefpass bestehend aus einem Widerstand und einer Kapazität
kennen. Die Wechselspannung am Ausgang UA war eine Funktion der Frequenz. In diesem Verusch wurde
ein aktiver Tiefpass realisiert. Dazu wird ein freuquenzabhängiges Bauelement zur Gegenkopplung eines
OPV so in invertierender Schaltung eingefügt, dass die Gegenkopplung bei steigender Frequent wächst. Man
erhählt einen aktiven Tiefpass, dessen Schematischer Aufbau in Abbildung 1 dargestellt ist. Um den
Frequenzgang dieses aktiven Filters berechnen fassen wir die Elemente zu den Impedanzen Z1 (ω und Z2 ω)
zusammengefasst. Für die Ausgangsspannung ergibt sich nun
UA (ω) = −
Z2 (ω)
· UE
Z1 (ω)
Dabei sind die Impendanzen gegeben durch
Z1 = R1
und Z2 (ω) =
1
R2
1
R2
=
1 + iωCR2
+ iωC
Die komplexe Spannungsverstärkung ergibt sich also zu
v(ω) = −
Z2 (ω)
R2
=−
Z2 (ω)
R1 (1 + iωC · R2 )
Die Grenzfrequenz dieser Schaltung bezeichnet dabei den Wert, bei dem die Verstärkug auf
Dies tritt ein, wenn Real- und Imaginärteil gleich sind also bei ω0 =
v(ω) =
1
R2 ·C .
√1
2
gesunken ist.
Es gilt
R2
1
r
2
R1
1 + ωω0
Im zweiten Versuchsteil wurde ein Selektivverstärker (Abbildung 2) realisiert. Dabei ist die Resonanzfrequenz
der Schaltung gegeben durch
1
√
ω0 =
C · R2 · R3
und die Verstärkung beträgt
v(ω) =
UE0
2iω · C · R3 + 1 − ω 2 · C 2 · R2 · R3
=
UA
iω · C · (2R3 + R2 ) + 1 − ω 2 · C 2 · R2 · R3
UE0 ist die Spannung die Hinter dem Widerstand R1 abgegriffen wird.
2
3 Schaltung und verwendete Messgeräte
Abbildung 1: schematischer Aufbau: aktiven Tiefpass
Abbildung 2: Schaltung eines Selektivverstärker
Zur Messung wurden folgende Messinstrumente verwendet:
• LMV181A Röhrenvoltmeter
• Oszillograph
• LCR-Messbrücke
3
4 Messwerte
Aufgabe 1 b)
Abbildung 3: Messwerte für Spannungsverstärkung am aktiven Tiefpass
4
Aufgabe 2 b)
Abbildung 4: Messwerte für Spannungsverstärkung am selektiven Verstärker 1
5
Abbildung 5: Messwerte für Spannungsverstärkung am selektiven Verstärker 2
6
5 Auswertung
Aufgabe 1b)
Abbildung 6: v(ω) am aktiven Tiefpass
Die Grenzfrequenz der Schaltung ergibt sich zu:
1
1
=
= 268.1Hz
2πR2 C
2π · 267.4kΩ · 2.22nF
q
q
2
2
B 2 − 26.93
26.932 − 26.93
2
2
=
=
= 264.5Hz
√
√
2πA 26.93
2π · 6.01732 · 10−4 26.93
2
2
theoretisch: fg =
gefittet:fgp
Die theoretische und experimentellen Ergebnisse stimmen annährend überein.
7
Aufgabe 1c)
Für den aktiven Tiefpass wurde das typische Integrationsverhalten beobachtet. Eine aussreichend unverzerrte Integration wurde ab 8kHz erreicht. Im vorhergehenden Frequenzbereich konnten die Aufund Entladekurven des Kondensators noch deutlich erkannt werden. Die Phase wird durch den OPV
um π gedreht und ausserdem durch den Kondensator noch um π2 . Dies konnte bei der Durchführung
beobachtet werden. Die gesamte Phasenverschiebung beläuft sich also auf π2 .
Abbildung 7: Integrationsverhalten des aktiven Tiefpasses bei 330Hz (Auf- und Entladekurven)
Abbildung 8: Integrationsverhalten des aktiven Tiefpasses bei 15kHz (Dreiecksfunktion)
8
Aufgabe 2b)
Abbildung 9: v(ω) am selektiven Vertärker
Aufgabe 2c)
Aus Abbildung 4,5 und 9 liest man die Halbwertsbreite ≈ 570Hz ab. Ausserdem bestimmt sich die
Resonanzfrequenz zu ≈ 1329Hz. Der theoretische Wert für die Resonanzfrequenz beläuft sich auf:
fr =
1
1
√
√
= 1382Hz
=
2πC R2 R3
2π · 2.23nF 267.4kΩ · 9.977kΩ
was nahe an den gemessenen Wert heran reicht. Der theoretische Wert für die Halbwertsbreite errechnet
sich zu 524Hz. Wie in folgendem Matlabgraphen zu erkennen(Grafik aus theoretischen Werten).
9
Abbildung 10: v(ω) am selektiven Vertärker theoretischer Verlauf(Eingangsspannung ist nicht die selbe wie
in Abb. 9)
Der theoretische stimmt, innerhalb einer Fehlertoleranz, mit dem gemessenen Wert überein. Die Abweichungen ergeben sich vor allem durch versteckte Widerstände, Kapazitäten und Induktivitäten im
Schaltungsaufbau selbst.
10
6 Diskussion
Dieser Versuch gestaltete sich reibungslos da er auf den Versuchen "Filter zur frequenzseletiven Messung"
und "Messung kleiner Spannungssignale - Verstärker II" aufbaut und so die Idee der aktiven Filter nahe
bringt. Die gemessenen Werte stimmten so allesamt gut mit der Theorie überein. Der in Abbildung 6 gemessene Frequenzgang der Verstärkung (am Tiefpass) ist in den Grundlagen theoretisch geschildert. Auch
das Frequenzverhalten der Übertragerfunktion am Wechselspannungsverstärker stimmt mit den erwarteten
Resultaten überein was ein Vergleich der Abbildung 9 und 10 verdeutlich. Zu Abbildung 6 ist anzumerken,
dass beim zügigen Aufnehmen der Messwerte ein Teil der Messung im unteren Skalenbereih des Röhrenvoltmeters statt fand, sodass wir die Fehlerbalken entsprechend größer zeichneten. Lediglich in Unteraufgabe 2
c kam es zu kleinen Problemem. Die Formel für die Spannungsverstärkung am Selektivverstärker beschreibt
das Verhältnis von Ausgangsspannung zur Eingangsspannung hinter R1 . Wir haben jedoch UE vor R1 abgeriffen, was zu einer letzdendlich höheren Kurve führt. Die Linearität ist unserer Meinung trotzdem bewart,
sodass die Grenzfrequnz sowieso, und die Halbwertsbreite,bezogen auf den niedrigeren Peak, mit der Messung
übereinstimmen muss, was sie auch offensichtlich tat.
11