Oologische Berechnungen

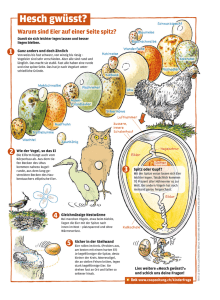
Oologische Berechnungen
Kurt Schläpfer
Man muss nicht Ornithologe sein, um über die Charakterisierung von Eiern mittels Zahlen und Formeln schreiben zu können, da es sich hier weitgehend um angewandte Geometrie
handelt. Allerdings sind einige Eiformen geometrisch nicht
einfach zu beschreiben, sodass es notwendig ist, Näherungsformeln abzuleiten und deren Brauchbarkeit mit gemessenen
Daten zu vergleichen. Der Autor des folgenden Beitrages ist
bei weitem nicht der Erste, der sich mit diesem Thema befasst.
Der weitaus wichtigste Beitrag auf diesem Gebiet stammt vom
Ornithologen Max Schönwetter, der in seinem vierbändigen
Handbuch über Oologie ungefähr 180 Seiten diesem Thema
gewidmet hat. Da diese Abhandlung bereits 1982 erschienen
ist, hat der Autor des vorliegenden Beitrags den Vorteil, dass
er auch noch spätere Erkenntnisse auf diesem Gebiet einbeziehen konnte.
Eiformen
Grundsätzlich kann man in der Tierwelt sechs Grundtypen von
Eiformen (siehe Abbildung) unterscheiden, nämlich
1 rund
2 elliptisch
3 rund-elliptisch, auch als walzenförmig bezeichnet
4 spitz-elliptisch
5 eiförmig (gleichbedeutend mit oval)
6 kegelförmig.
Die sechs Grundtypen von Eiformen
2
Viele Eier sind Mischformen oder Varianten dieser sechs
Grundtypen. Ein ovales Ei kann beispielsweise dicker oder
schmaler, aber auch länglicher oder kürzer als das hier abgebildete Beispiel Nr. 5 sein. Allein von dieser Eiform sind somit fast beliebige Varianten möglich. Übereinstimmend mit
dem Buchtitel des Ornithologen Makatsch kann man daher
sagen: «Kein Ei gleicht dem anderen». Die hier gezeigten Eiformen sind aber insofern wichtig, als sich damit die zahlenmässige Beschreibung der Eier erklären lässt.
Die einfachste Eiform ist die Kugel. Sie benötigt zur Beschreibung nur eine einzige Zahl, nämlich den Durchmesser.
Es gibt aber nur wenige Tierarten, die kugelförmige Eier legen. Bei den Vögeln sind es einige Eulenarten, der Steinkauz
und der Eisvogel, und bei den Reptilien sind es einige Schildkröten- und Geckoarten. Bei allen übrigen Eiformen braucht es
zur Beschreibung mindestens eine Längen- und eine Breitenangabe. Entspricht die Eiform einem Ellipsoid, genügt die
Angabe der Länge und der Breite für eine exakte Beschreibung. Oft werden diese beiden Grössen als Verhältniszahl
angegeben, um zu beschreiben, wie gestreckt eine bestimmte
Eiform ist. Dieser Wert ist im Fall einer idealen Kugelform 1.0
und kann bei Vogeleiern nicht grösser als 1.9 sein. Bei
Schlangeneiern kann dieser Wert bis 10.0 betragen.
Beispiele für das Verhältnis von Eilänge zu -breite:
Vögel:
1.0 bis 1.9
Krokodile:
1.4 bis 1.8
Schlangen:
1.3 bis 10.0
Schildkröten: 1.0 bis 2.4
Geckos:
1.0 bis 4.3
3
Bei Hühnereiern ist das Verhältnis von Länge zu Breite 1.33.
Eine relativ exakte elliptische Form haben die Eier von Krokodilen, Schwänen und Gänsen. Es gibt aber auch elliptische
Eier, die an den beiden Enden entweder runder oder spitzer
sind als ein geometrisches Ellipsoid (siehe Eiformen Nr. 3 und
4). Wenn die Eier an den beiden Enden sehr rund sind, kann
man sie als walzenförmig bezeichnen. Diese Form findet sich
bei vielen Schlangeneiern. Es ist zwar möglich, den Grad der
Rundheit an den beiden Enden zu spezifizieren, aber solche
Grössen sind unanschaulich und finden sich daher nicht in der
Beschreibung von Eiformen. Eine sehr häufige Eiform, die
aber nur bei Vögeln vorkommt, ist die ovale Form, geometrisch als Ovoid bezeichnet. Bei dieser Form befindet sich die
maximale Breite nicht mehr in der Mitte der Längsachse, sodass das Ei ein rundes und ein spitzes Ende hat. Wenn die
maximale Breite sehr stark verschoben ist, kann das Ei sogar
kegelförmig aussehen (siehe Eiform Nr. 6). Eiformen dieser
Art kann man genauer beschreiben, wenn man den Betrag
angibt, um welchen die maximale Dicke von der Mitte der
Längsachse abweicht.
Volumen
Im Falle von kugelförmigen Eiern kann das Volumen V (ml)
aus dem Durchmesser D (cm) wie folgt berechnet werden:
V = 0.5236 × D3
(1)
Bei einer exakt elliptischen Eiform errechnet sich das Volumen aus der Länge L und der Breite B:
4
V = 0.5236 × L × B2
(2)
Bei allen anderen Eiformen sind die Länge und die Breite allein nicht ausreichend für eine exakte Berechnung des Volumens. Da die meisten Eier nicht exakt elliptisch sind, resultiert
bei der Anwendung von Formel (2) ein Fehler, der jedoch für
die meisten Eiformen nicht grösser als 2% ist. Um diesen Fehler noch zu minimieren, kann bei Vogeleiern anstatt mit
0.5236 mit dem Faktor 0.51 gerechnet werden. Bei den relativ
seltenen kegelförmigen Eiern liegt dieser Faktor unter 0.5.
Beim Ei der Trottellumme (Uria aalge) beträgt er beispielsweise 0.46. Umgekehrt liegt dieser Wert bei walzenförmigen
Eiern über 0.55. Der Wert hängt zudem bei dieser Eiform vom
Verhältnis Eilänge zu -breite ab. Eine brauchbare Näherungsformel zur Berechnung des Volumens von walzenförmigen
Eiern ist:
V = 0.131 × B2 × (5L – B)
(3)
Gewicht
Wenn man das Volumen kennt, ergibt sich das Gewicht G (g),
indem man das Volumen V (ml) mit dem spezifischen Gewicht gspez multipliziert:
G = V × gspez
(4)
Allerdings ist das spezifische Gewicht in der Regel nicht bekannt. Bei Vogeleiern kann es zwischen 1.05 und 1.14 variieren. Nimmt man bei der Berechnung des Gewichts eine Ungenauigkeit von ± 4% in Kauf, kann man mit einem mittleren
Wert von 1.09 rechnen. Dies gilt aber nur für Vogeleier. Bei
5
Reptilieneiern kann das spezifische Gewicht bis 1.26 betragen.
Wenn man hier mit einem mittleren Wert rechnen würde, wäre
die Ungenauigkeit bei der Berechnung des Eigewichts zu
gross. Es gilt jedoch die grobe Regel, dass das spezifische
Gewicht mit zunehmender Eigrösse zunimmt. So entspricht
bei den Vogeleiern der kleinste Wert von 1.05 tatsächlich auch
dem kleinsten Ei, und der Wert 1.14 gilt für das grösste Vogelei, nämlich das Straussenei. Aber man kann keine exakte
Beziehung zwischen der Eigrösse und dem spezifischen Gewicht ableiten, da die Dicke der Eischale eine Rolle spielt, und
diese für gleich grosse Eier durchaus verschieden sein kann.
Bei Reptilieneiern liegt aber das spezifische Gewicht für ein
Eivolumen von unter 20 ml fast immer im Bereich von 1.05
bis 1.15. Rechnet man somit mit einem mittleren Wert von
1.10, beträgt der Fehler in der Regel nicht mehr als 5%. Und
wenn das Eivolumen unter 1 ml liegt (was für viele Reptilieneier zutrifft) kann man sogar noch genauer mit einem mittleren spezifischen Gewicht von 1.07 rechnen.
Präziser lässt sich das Gewicht bestimmen, wenn man das
Gewicht GS (g) des leeren Eis, also der Eischale, kennt. Da das
spezifische Gewicht eines Eis ohne Schale stets 1.03 beträgt,
kann man wie folgt rechnen:
Gewicht = Volumenohne Schale × 1.03 + Gs
(5)
Da man allerdings das Volumen ohne Schale nicht kennt, kann
man folgende gute Näherungsgleichung verwenden:
G = (1.03 × V) + (0.5 × GS)
(6)
6
Oft ist auch die Dicke der Eischale bekannt, da diese an zerbrochenen Eischalen leicht gemessen werden kann. Während
die Schalendicke bei Vogeleiern von 0.032 mm bis 2.5 mm
reicht, liegt sie bei Reptilieneiern in einem Bereich von 0.029
mm bis 0.72 mm. Dass die dickste Eischale bei Reptilien über
dreimal dünner ist als bei den Vögeln hat damit zu tun, dass
Reptilieneier auch kleiner sind als Vogeleier. Das grösste Reptilienei, nämlich das Ei der Riesenpython erreicht nicht einmal
die Grösse eines Schwaneneis. Leider hat der Autor dieses
Beitrages keine brauchbare Formel gefunden, um aus der Dicke der Eischale das Gewicht der Eischale oder das spezifische
Gewicht berechnen zu können.
Umfang
Meist wird als Masstab für die Ei-Grösse das Gewicht verwendet. Betrachtet man aber Eier in einer Sammlung oder in
fotografischen Abbildungen, so nimmt man die Grösse eines
Eis primär durch seine Dimensionen wahr, nämlich durch die
Länge und Breite. Diese beiden Grössen kann man zweckmässig mit einer einzigen Zahl, nämlich mit dem Umfang beschreiben. Dabei ist die Feststellung wichtig, dass der Umfang
nicht direkt mit dem Gewicht zusammenhängt, und Eier von
gleichem Umfang unterschiedlich schwer sein können, nämlich dann, wenn sie ein unterschiedliches Verhältnis von Länge und Breite besitzen. Dies sei an folgendem Beispiel illustriert:
Ei Nr. 1
Ei Nr. 2
Länge
(cm)
7.7
10.0
Breite
(cm)
7.7
5.0
L/B
1.0
2.0
Umfang
(cm)
24.2
24.2
7
Gewicht
(Gramm)
309
127
Der Umfang von Ei Nr. 2 wurde unter Annahme einer exakten
Ellipsenform berechnet. Für die Gewichtsberechnung wurde
ein spezifisches Gewicht von 1.1 angenommen.
Das Beispiel zeigt, dass das Ei Nr. 1, das kugelförmig ist, bei
gleichem Umfang mehr als doppelt so schwer ist wie das längliche Ei Nr. 2, das nur halb so breit wie lang ist.
Der Umfang ist zwar eine einfach definierte Grösse, die aber
für fast alle Eiformen nicht exakt berechnet werden kann,
wenn man nur die Länge und Breite des Eis kennt. Einzig bei
kugelförmigen Eiern kann man den Umfang U (cm) exakt aus
dem Durchmesser D (cm) berechnen:
U = 3.14 × D
(7)
Für alle anderen Eiformen benötigt man Näherungsformeln.
Eine gute Näherungsformel, deren Qualität allerdings stark
vom Verhältnis von Eilänge zu Eibreite abhängt, lautet:
U = 1.57 × (L + B)
(8)
Für ein Seitenverhältnis, das nicht grösser ist als 2:1, beträgt
der Fehler mit dieser Formel weniger als 4%. Diese Formel
kann daher auf alle Vogeleier angewendet werden. Bei Reptilieneiern, die ein Seitenverhältnis von bis zu 10:1 haben können, rechnet man ab einem Verhältnis von 2:1 genauer mit der
folgenden Formel:
U = 2L + B
(9)
8
Beispiel für die Volumen- und Gewichtsberechnung
Daten gemessen an einem Hühnerei (Gallus gallus domesticus):
Eilänge:
60.0 mm
Eibreite:
42.3 mm
Ei-Gewicht:
59.9 g
Ei-Volumen:
55.0 ml
Schalengewicht:
5.0 g
Volumen berechnet nach Formel (2):
V = 56.21 ml (Fehler 2.2%)
Volumen berechnet nach Formel (2) mit dem Faktor 0.51:
V = 54.75 ml (Fehler 0.5%)
Gewicht berechnet nach Formel (4) mit dem spez. Gewicht von 1.09:
G = 59.95 g (Fehler unter 0.1%)
Gewicht berechnet nach Formel (6) mit dem Schalengewicht 5.0:
G = 59.15 (Fehler 1.3%)
Adresse des Autors:
Kurt Schläpfer, St. Gallerstrasse 60, CH-9032 Engelburg
[email protected]
März 2012
9