Übungsaufgaben zur E1 / E1p Mechanik, WS 2016/17 Prof. J. O.

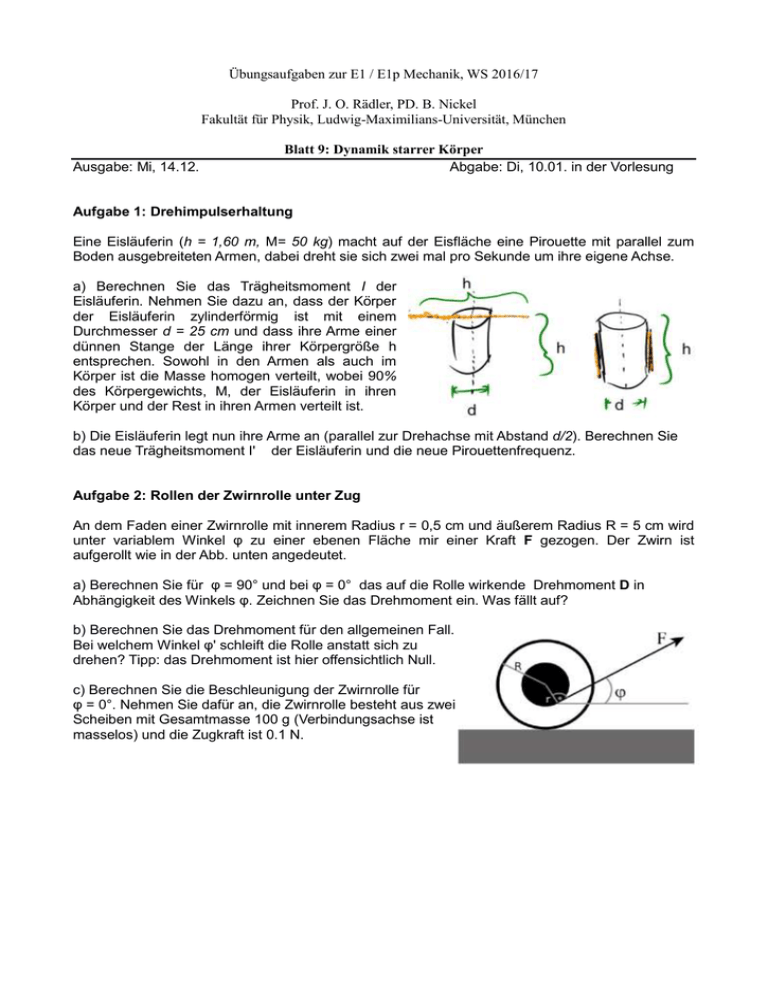
Übungsaufgaben zur E1 / E1p Mechanik, WS 2016/17
Prof. J. O. Rädler, PD. B. Nickel
Fakultät für Physik, Ludwig-Maximilians-Universität, München
Ausgabe: Mi, 14.12.
Blatt 9: Dynamik starrer Körper
Abgabe: Di, 10.01. in der Vorlesung
Aufgabe 1: Drehimpulserhaltung
Eine Eisläuferin (h = 1,60 m, M= 50 kg) macht auf der Eisfläche eine Pirouette mit parallel zum
Boden ausgebreiteten Armen, dabei dreht sie sich zwei mal pro Sekunde um ihre eigene Achse.
a) Berechnen Sie das Trägheitsmoment I der
Eisläuferin. Nehmen Sie dazu an, dass der Körper
der Eisläuferin zylinderförmig ist mit einem
Durchmesser d = 25 cm und dass ihre Arme einer
dünnen Stange der Länge ihrer Körpergröße h
entsprechen. Sowohl in den Armen als auch im
Körper ist die Masse homogen verteilt, wobei 90%
des Körpergewichts, M, der Eisläuferin in ihren
Körper und der Rest in ihren Armen verteilt ist.
b) Die Eisläuferin legt nun ihre Arme an (parallel zur Drehachse mit Abstand d/2). Berechnen Sie
das neue Trägheitsmoment I' der Eisläuferin und die neue Pirouettenfrequenz.
Aufgabe 2: Rollen der Zwirnrolle unter Zug
An dem Faden einer Zwirnrolle mit innerem Radius r = 0,5 cm und äußerem Radius R = 5 cm wird
unter variablem Winkel φ zu einer ebenen Fläche mir einer Kraft F gezogen. Der Zwirn ist
aufgerollt wie in der Abb. unten angedeutet.
a) Berechnen Sie für φ = 90° und bei φ = 0° das auf die Rolle wirkende Drehmoment D in
Abhängigkeit des Winkels φ. Zeichnen Sie das Drehmoment ein. Was fällt auf?
b) Berechnen Sie das Drehmoment für den allgemeinen Fall.
Bei welchem Winkel φ' schleift die Rolle anstatt sich zu
drehen? Tipp: das Drehmoment ist hier offensichtlich Null.
c) Berechnen Sie die Beschleunigung der Zwirnrolle für
φ = 0°. Nehmen Sie dafür an, die Zwirnrolle besteht aus zwei
Scheiben mit Gesamtmasse 100 g (Verbindungsachse ist
masselos) und die Zugkraft ist 0.1 N.
Aufgabe 3: Präzession eines Gyroskops
Ein Gyroskop besteht aus einer Scheibe (m = 0.3 kg, 𝐼 = 0.5 𝑘𝑔 𝑚2 ), die um eine Drehachse 
durch den Mittelpunkt der Scheibe rotiert. Der Abstand der Scheibe vom Lagerpunkt bei A sei b =
20 cm. Die Winkelgeschwindigkeit der Scheibe ist 𝜔 = 0.2 𝑟𝑎𝑑/𝑠. Der Winkel zwischen der
Drehachse  und der Senkrechten ist .
a) Wenn das Gyroskop mit einer Neigung = 90° gestartet
wird, ändert die Drehachse  kontinuierlich ihre Richtung.
Diese
Bewegung
nennt
man
Präzession.
Die
Präzessionswinkelgeschwindigkeit  ist definiert als die
Winkelgeschwindigkeit, mit der  und damit auch der
Drehimpuls L seine Richtung ändert. Wir wählen auf Grund der
beobachteten Präzession folgenden Ansatz:
cos Ωt
𝑳 = |𝑳| ( sin Ωt ). Berechnen Sie damit dL/dt.
0
b) Allgemein gilt dL/dt = D. D ist hier das Drehmoment, das aus
der Gravitationskraft der Scheibe und dem Lagerpunkt bei A
resultiert (die Achse ist masselos). Berechnen Sie D für  = 90°.
*c) Berechnen Sie nun aus Kombination der Ergebnisse aus (a) und (b) die Präzessionsgeschwindigkeit . Wie ändert sich  für  < 90°?
Aufgabe 4: Statisches Gleichgewicht
a) Zwei Körper mit dreieckigem und quadratischem
Querschnitt mit Kantenlänge L werden gegenüber der
Horizontalen gekippt. Berechnen Sie den kritischen
Winkel , bis zu dem ein stabiles Gleichgewicht vorliegt.
b) Ein dünner Stab der Länge l und Masse m, welcher
anfangs aufrecht auf einem reibungsfreien Tisch steht, fängt
an zu fallen. Beschreiben Sie qualitativ die Bewegung des
Schwerpunkts und die des Stabes.
*c) Stellen Sie die Energiebilanz für seine Bewegung auf und
bestimmen Sie die Geschwindigkeit des Schwerpunkts als
Funktion seiner Position.