5. Energieumwandlungen als reversible und nichtreversible Prozesse

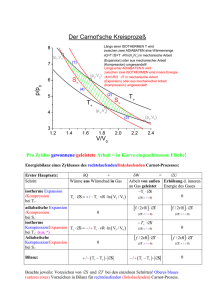
5. Energieumwandlungen als reversible und nichtreversible Prozesse
5.1 Reversibel-isotherme Arbeitsprozesse
Energiebilanz für geschlossene Systeme
Für isotherme reversible Prozesse gilt
und daher
Dies definiert die freie innere Energie:
Die maximale abgegebene Arbeit
in geschlossenen isothermen
Systemen ist durch die Differenz der freien inneren Energie
gegeben.
5.1-1
Energiebilanz für stationäre offene Systeme
Für isotherme reversible Prozesse gilt:
Dies definiert die freie Enthalpie auch Gibbssche Enthalpie:
Die maximale abgegebene Leistung
freien Enthalpieströme
ist durch die Differenz der
und durch die Änderungen der
kinetischen und potentiellen Energie gegeben.
5.1-2
5.2 Berücksichtigung von Dissipation
Isentroper Wirkungsgrad eines adiabaten Arbeitsprozesses
in einer Turbine
real:
isentrop:
Analog folgt für den Verdichter:
(Die grauen Zustandsänderungen sind
bei adiabaten Prozessen unzulässig)
Wird zur Charakterisierung realer Fließprozesse in der Auslegung
von Kreisprozessen benutzt
5.2-1
5.3 Reversible Kreisprozesse
Beispiel: Der Carnot-Prozess
(Darstellung im T, s-Diagramm)
1 - 2 reversibel adiabat
2 - 3 reversibel isotherm
3 - 4 reversibel adiabat
4 - 1 reversibel isotherm
Kreisprozess:
5.3-1
5.3-1 Das Dampfkraftwerk: der Clausius-Rankine-Prozess
0 – 1 : isentrope Kompression der
Flüssigkeit durch Zufuhr von Arbeit:
1 – 2 : komprimierte Flüssigkeit wird
durch Wärmezufuhr verdampft und
überhitzt:
2 – 3 : isentrope Entspannung ins
Nassdampfgebiet in der Turbine mit der
Abfuhr von Arbeit:
3 – 0 : isobare und isotherme
Wärmeabfuhr durch Kondensation des
Dampfanteils:
5.3-2
Der Clausius-Rankine-Prozess im h,s-Diagramm
5.3-3
Bilanz des reversiblen Kreisprozesses
Thermodynamische Mitteltemperatur Tm,12 definiert durch:
Energiebilanz:
5.3-4
Beispiel:
0 – 1 Kompression der Flüssigkeit,
(Tabelle A1.2 (Lucas)):
1 – 2 Wärmezufuhr
Zustand 2: Überhitzter Dampf bei
Durch Interpolation:
5.3-5
2 – 3 Expansion ins Nassdampfgebiet
Zustand 3 gegeben durch
und
Sättigungszustand bei p = 10 kPa
Abgegebene Arbeit:
Wirkungsgrad:
5.3-6
5.3-2 Die Gasturbine: der Joule-Prozess oder Brayton-Prozess
Offene Gasturbinenanlage
Geschlossene Gasturbinenanlage als
Vergleichsprozess
Druckverhältnis:
5.3-7
Darstellung der Gasturbine im T,s-Diagramm
Bilanz des Kreisprozesses
Abgegebene Nettoarbeit:
Thermischer Wirkungsgrad
Vereinfachende Annahmen:
Luft als ideales Gas, konst. Cp
reversible Prozessschritte
5.3-8
1–3
Reversibel-adiabate Kompression
Zugeführte Arbeit
3–4
Durch Verbrennung zugeführte Wärme
4–6
Reversibel-adiabate Expansion
Abgeführte Arbeit
6–2
Durch Kühlung abgeführte Wärme
5.3-9
Thermischer Wirkungsgrad der Gasturbine
5.3-10
Beispiel: Nichtreversible geschlossene Gasturbinenanlage
Isentrope Strömungsmachinenwirkungsgrade:
Verdichter:
Zustand 1:
Zustand 3:
Gaserhitzer:
Zustand 4:
Turbine:
Zustand 6:
5.3-11
Gasturbinenprozess im T,s-Diagramm
Energiebilanz:
(Arbeitsmedium als ideales Gas mit konst.
spez. Wärmen approximiert)
5.3-12
Abgeführte Arbeit:
Zugeführte Wärme:
Thermischer Wirkungsgrad:
Vergleich mit Joule-Prozess:
5.3-13
5.3-3 Das Strahltriebwerk
Aus der Definition der Arbeit der Schubkraft
folgt für die
Vortriebsleistung PV , die der Arbeit des Prozesses entspricht:
Bei Vernachlässigung des Brennstoffmassenstroms errechnet sich die
Schubkraft aus der Impulsänderung des Luftstromes:
5.3-14
Der Vergleichsprozess für das Strahltriebwerk besteht aus einem im geschlossenen
Kreislauf geführten Luftstrom, dem beim Zustand 0 und 5 kinetische Energien zubzw. abgeführt werden. Der Abgasverlust auf Grund der hohen Abgastemperatur
wird durch eine Kühlung des Luftstroms dargestellt.
5.3-15
Darstellung des Strahltriebwerks im T,s-Diagramm:
5.3-16
1–2
Reversibel-adiabate Verdichtung ohne Arbeitszufuhr durch
Geschwindigkeitsabsenkung auf
sind gegeben
Energiebilanz:
Isentrope Zustandsänderung:
2–3
Reversibel-adiabate Verdichtung mit Zufuhr von technischer
Leistung ohne Änderung kinetischer Energie, p3/p2 gegeben
5.3-17
3–4
Reversible Wärmezufuhr bei konstantem Druck,
gegeben
Energiebilanz:
Fundamentalgleichung
4–5
Reversibel-adiabate Expansion in der Turbine
Nebenbedingung: Turbine soll über die Welle den Verdichter antreiben,
keine Nettoarbeitsleistung
5.3-18
5–6
6–1
Reversibel-adiabate Expansion ohne Arbeitsleistung mit
Geschwindigkeitserhöhung
Notwendige Wärmeabfuhr um Prozess zu schließen
(erfasst den Verlust an thermischer Energie, die mit den heißen
Abgasen an die Umgebung abgeführt wird)
5.3-19
Wirkungsgrade
Innerer Wirkungsgrad:
Aus
folgt:
Das Druckverhältnis im Verdichter
ist Auslegungsparameter.
5.3-20
Energiebilanz am Gesamtprozess:
Innenwirkungsgrad:
Der Innenwirkungsgrad berücksichtigt die Umwandlung der zugeführten
Wärme in die Änderung der kinetischen Energie
Thermischer Wirkungsgrad des Kreisprozesses:
Außenwirkungsgrad:
Der Außenwirkungsgrad
berücksichtigt die Umwandlung von
kinetischer Energie in Vorschubleistung
5.3-21
Beispiel:
(durch maximale thermische Belastung der ersten
Turbinenschaufel vorgegeben),
Lösung:
5.3-22
5.3-23
Wirkungsgrade für das Beispiel:
Umwandlung der zugeführten Wärme in kinetische Energie:
Umwandlung von kinetischer Energie in Vorschubleistung:
Thermischer Wirkungsgrad:
5.3-24
5.3-4 Verbrennungsmotoren
5.3-25
Der idealisierte Otto-Prozess (Gleichraumprozess)
•
Vernachlässigung von Verlusten ↔ Annahme eines reversiblen Prozesse
•
Massenaustausch mit der Umgebung (Ein- und Ausschieben) bleibt
unberücksichtigt
•
die mit der Materie transportierte Energie wird durch Wärmeabfuhr ersetzt
•
Kompression und Expansion werden als reversibel-adiabate Prozesse
aufgefasst.
•
Wärmezufuhr und Wärmeabfuhr erfolgen bei konstantem Volumen.
5.3-26
Darstellung im p,V-Diagramm
5.3-27
Darstellung im T,S-Diagramm
5.3-28
Bilanz des Kreisprozesses
Volumenänderungsarbeiten
Wärmezufuhr und –abfuhr
5.3-29
Thermischer Wirkungsgrad
Wegen der isentropen Kompression und Expansion gilt:
Für die isochoren Prozesse und ideales Gas gilt andererseits:
und daher
5.3-30
Der thermische Wirkungsgrad des Otto-Prozesses ist wegen T3 > T2 stets kleiner als
der Wirkungsgrad des Carnot-Prozesses zwischen den Temperaturen T3 und T1.
Mit den isentropen Zustandsänderungen
kann mit dem Kompressionsverhältnis
geschrieben werden:
5.3-31
Der thermischer Wirkungsgrad des idealisierten Ottoprozesses ist daher nur eine
Funktion des Verdichtungsverhältnisses:
Für
*)
Der Wirkungsgrad steigt mit dem Verdichtungsverhältnis
an.
*)
Werden Wärmeverluste bei Kompression und Expansion und andere Verluste berücksichtigt, so
kann statt des Isentropenexponenten κ auch ein adäquater Polytropenexponent n verwendet werden.
5.3-32
Der idealisierte Diesel-Prozess (Gleichdruckprozess)
•
Vernachlässigung von Verlusten ↔ Annahme eines reversiblen Prozesse
•
Ein- und Ausschiebeprozesse bleiben wiederum unberücksichtigt.
•
Kompression und Expansion werden als reversibel-adiabate Prozesse
aufgefasst.
•
Wärmezufuhr erfolgt bei konstantem Druck.
•
Wärmeabfuhr erfolgt bei konstantem Volumen.
5.3-33
Darstellung im p,V-Diagramm
5.3-34
Darstellung im T,S-Diagramm
5.3-35
Bilanz des Kreisprozesses:
Volumenänderungsarbeiten:
Wärmezufuhr und –abfuhr:
5.3-36
Thermischer Wirkungsgrad des Diesel-Vergleichsprozesses:
5.3-37
Aus dem T,S-Diagramm liest man ab:
Entropiedifferenz bei isobarer Wärmezufuhr:
Entropiedifferenz bei isochorer Wärmeabfuhr:
Daher gilt:
Wir definieren ein Maß, das die Volumenzunahme bei der Wärmezufuhr
(Verbrennung) darstellt:
5.3-38
Wegen p =const ist dann:
Wegen der isentropen Zustandsänderung gilt:
Daher gilt:
5.3-39
Beim Gleichdruckprozess ist die Brennstoffausnutzung umso besser, je höher das
Verdichtungsverhältnis und je kleiner die Belastung der Maschine ist ϕ → 1 (das
heißt T3 → T2, bzw. keine Brennstoffeinspritzung).
Der Wirkungsgrad geht dann in den des Otto-Prozesses (Gleichraumprozess) über.
Das Verdichtungsverhältnis kann man jedoch viel höher einstellen als beim OttoProzess, da keine Selbstzündungsgefahr vorliegt, weshalb man den Brennstoff
wesentlich besser ausnutzen kann.
In der Praxis erreicht der Diesel-Motor deshalb einen besseren Wirkungsgrad als
der Otto-Motor.
5.3-40
5.3-5 Die reversible Wärmepumpe
Eine Wärmepumpe soll Wärme bei niedriger Temperatur aufnehmen und bei
einem höheren Temperaturniveau abgeben.
Die Leistungszahl ε bezeichnet das Verhältnis von Zielgröße, hier der zum
Heizen bereitgestellten Wärme, zur dafür aufgewendeten technischen Leistung.
Für einen reversiblen Kreisprozess gilt
und
(1. Hauptsatz)
.
( 2. Hauptsatz)
Daraus folgt für die Leistungszahl:
5.3-41
5.3-6 Die Gaskältemaschine mit innerem Wärmeaustausch
T,s-Diagramm
Kältemaschine arbeitet zwischen
den Drücken
5.3-42
Arbeiten:
Reversibel-adiabate Verdichtung
Reversibel-adiabate Leistungsabgabe
Wärmen:
Wärmeabfuhr im Kühler
Wärmeaufnahme im Kühlraum
(Umgebungstemperatur)
5.3-43
Leistungsziffer:
(Nutzen q56, Aufwand Σwt )
5.3-44
Leistungsziffer ohne Wärmetauscher:
5.3-45