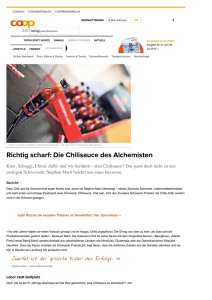
Uebungsblatt 07 fuer PHYS3100 Grundkurs IIIb

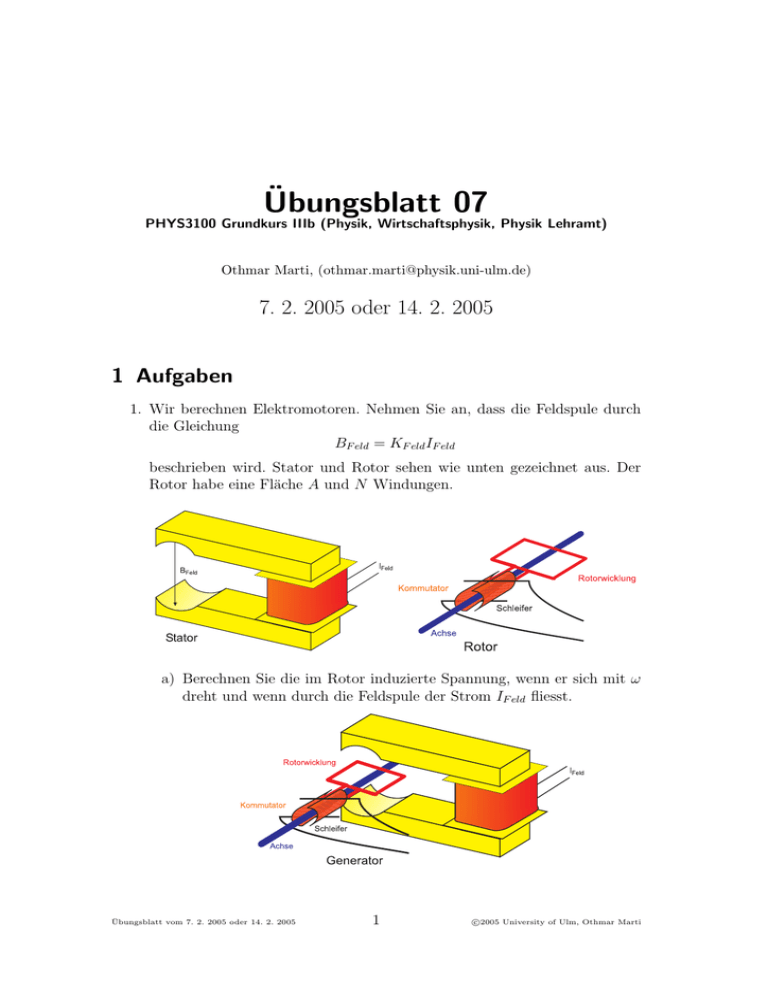
Übungsblatt 07
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, ([email protected])
7. 2. 2005 oder 14. 2. 2005
1 Aufgaben
1. Wir berechnen Elektromotoren. Nehmen Sie an, dass die Feldspule durch
die Gleichung
BF eld = KF eld IF eld
beschrieben wird. Stator und Rotor sehen wie unten gezeichnet aus. Der
Rotor habe eine Fläche A und N Windungen.
a) Berechnen Sie die im Rotor induzierte Spannung, wenn er sich mit ω
dreht und wenn durch die Feldspule der Strom IF eld fliesst.
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
1
c
°2005
University of Ulm, Othmar Marti
2
PHYS 3110 Grundkurs IIIb WH 2004-2005
Übungsblatt 07
b) Berechnen Sie die konstante Spannung, die an einem Widerstand die
gleiche Verlustleistung erzeugt wie wenn an dem Widerstand die durch
den sich mit ω drehenden Generator erzeugte Spannung anliegt (die
effektive Spannung).
c) Berechnen Sie für einen Nebenschlussmotor das Drehmoment M (ω).
d) Berechnen Sie für einen Hauptschlussmotor das Drehmoment M (ω).
2. Wie gross ist die Larmorfrequenz im Erdmagnetfeld?
3. An ein Gas, dessen Atome ein intrinsisches magnetisches Dipolmoment
1.33 · 10−23 J/T haben, wird ein Magnetfeld von 0.5T angelegt. Bei welcher Temperatur wird die mittlere Translationsenergie der Gasatome gleich
gross wie die Energie, die benötigt wird, um einen Dipol auszurichten?
4. Ein Plattenkondensator besteht aus quadratischen Plattenmit einer Kantenlänge von 1m. Der Kondensator wird mit einem Strom von 2.0A geladen,
~ zwischen den Platten erzeugt.
der ein homogenes elektrisches Feld E
a) Wie steht dieses Feld zu den Platten?
b) Wie gross ist der Verschiebungsstrom durch den Bereich zwischen den
Platten?
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
2
c
°2005
University of Ulm, Othmar Marti
Übungsblatt 07
PHYS 3110 Grundkurs IIIb WH 2004-2005
3
c) Wie gross ist dE/dt in diesem Bereich?
d) Ein quadratischer Weg S mit einer Kantenlänge von 0.5m liege symmetrisch zu den Kondensatorplatten zwischen ihnen. Wie gross ist der
Verschiebungsstrom durch die durch diesen Weg aufgespannte Fläche?
H
~ · d~s entlang dieses Weges?
e) Wie gross ist B
5. Wir setzen U = 100V , R1 = 10Ω, R2 = 20Ω, R3 = 30Ω und L = 2H.
Berechnen Sie den Strom I2 durch R2 und den Strom I1 durch R1
a) unmittelbar nach dem Schliessen des Schalters S.
b) lange Zeit später.
c) unmittelbar nach dem erneuten Öffnen von S.
d) Lange nach dem Öffnen von S.
6. Zeigen Sie, dass das elektrische Feld in einem Plattenkondensator nicht
plötzlich auf Null abfallen kann, wenn wir uns quer zur Feldrichtung aus
dem Zwischenraum zwischen den Platten heraus bewegen. Hinweis: Wenden
Sie das Faradaysche Gesetz auf dem gestrichelt eingezeichneten Weg an.
7. Wie in der Abbildung haben wir zwei kreisförmige Bereiche mit den Radien
R1 = 0.2m und R2 = 0.3m.
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
3
c
°2005
University of Ulm, Othmar Marti
4
PHYS 3110 Grundkurs IIIb WH 2004-2005
Übungsblatt 07
In R1 zeigt ein homogenes Magnetfeld B1 = 0.1T nach hinten, in R2 ein
homogenes Magnetfeld von B2 = 0.15T nach vorn. Beide
Felder nehmen
H
~
mit der Geschwindigkeit 0.015T /s ab. Berechnen Sie E · d~s für jeden der
drei eingezeichneten Wege.
8. In der unten gezeichneten Schaltung habe C1 = 900µF , C2 = 100µF und
L = 10H.
C1 sei auf 100V aufgeladen, C2 sei entladen. Geben Sie eine genaue Anleitung, wie man den Kondensator C2 auf 300V aufladen kann, indem man S1
und S2 in geeigneter Weise schliesst und öffnet.
9. Der Maximalwert der Feldstärke einer ebenen Radiowelle betrage 5V /m.
berechnen Sie
a) den Maximalwert der magnetischen Feldstärke
b) und die Intensität der Welle.
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
4
c
°2005
University of Ulm, Othmar Marti
Übungsblatt 07
PHYS 3110 Grundkurs IIIb WH 2004-2005
5
2 Lösungen
1.
a) Wir betrachten zuerst den Elektromotor als Generator. Der Fluss
durch die Leiterschlaufe mit N Windungen und einer Fläche A ist
φB = N KF eld IF eld A cos Θ
wobei Θ der Winkel zwischen der Normalen der Fläche der Leiterschlaufe und der Richtung des Magnetfeldes ist. Mit Θ = ωt + δ wird
der zeitabhängige Fluss durch eine sich mit ω drehende Leiterschlaufe
φB (t) = N KF eld IF eld A cos(ωt + δ)
Durch Ableiten erhält man die Induktionsspannung
U =−
dφB (t)
d
= −N KF eld IF eld A cos(ωt+δ) = N KF eld IF eld Aω sin(ωt+δ)
dt
dt
b) Die Leistung an einem Widerstand ist
P (t) = U (t) · I(t) =
U (t)2
R
Wenn U (t) = U0 cos(ωt) ist, ist
U02
cos2 (ωt)
R
Nun ist das Integral über eine Periode
Z 2π
1
1
cos2 αdα =
2π 0
2
P (t) =
Die induzierte effektive Spannung (die die gleiche Verlustleistung wie
eine gleichgrosse Gleichspannung erzeugt) ist
Uef f,i =
N KF eld IF eld Aω
√
2
c) Wenn die Leiterschlaufe mit Spannung versorgt wird, arbeitet sie als
Motor. Durch den Strom I wird ein Drehmoment
M = N AKF eld IF eld · I · sin Θ
erzeugt1 . Das mittlere Drehmoment bei einem Motor, bei dem der
Kommutator immer bei dem Winkel, bei dem das Drehmoment null
wird, das Vorzeichen ändert, ist
Mef f =
1
N AKF eld IF eld
√
I = N AKF eld IF eld Ief f
2
Beachte die Phasenverschiebung zwischen Fluss und Drehmoment!
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
5
c
°2005
University of Ulm, Othmar Marti
6
PHYS 3110 Grundkurs IIIb WH 2004-2005
Übungsblatt 07
Wenn der Widerstand des Ankers, der rotierenden Spule, R ist, kann
man den mittleren Strom berechnen
Ief f =
U
N KF eld IF eld A
U − Uef f,i
√
= −
ω
R
R
R 2
Damit hängt das Drehmoment von der Drehzahl ab
¶
µ
N KF eld IF eld A
U
√
−
ω
Mef f (ω) = N AKF eld IF eld
R
R 2
N AKF eld IF eld U
N 2 A2 (KF eld IF eld )2
√
=
−
ω
R
2R
Das Drehmoment des ruhenden Motors ist also
Mef f (0) = Mmax =
N AKF eld IF eld U
R
und die maximale Drehzahl (da wo Mef f = 0) ist
√
2U
ωmax =
N AKF eld IF eld
Diese Charakteristik hat man immer dann, wenn das erregende Feld
KF eld IF eld unabhängig von der Drehzahl ist, bei Permanentmagneten
oder wenn die Spule für die Erregerwicklung parallel zum Anker angeschlossen ist. Will man die Drehzahl erhöhen, muss man das Feld
KF eld IF eld schwächer machen.
d) Ist die Erregerwicklung in Serie zur Ankerwicklung geschaltet, gibt es
keine maximale Drehzahl. Wir verwenden
BZ = KF eld I
Für andere Geometrien gilt das gleiche Gesetz, aber mit einem geometrieabhängigen Vorfaktor K. Im statischen Falle ist der Strom nur
vom Gleichstromwiderstand RE der Erregerspule abhängig. Wenn UE
der Spannungsabfall an der Erregerspule ist, ist
B(UE ) = K
UE
= KIE
RE
Der durch den Anker fliessende Strom ist dann durch
Ief f =
U
UE
N B(UE )A
U − UE − Uef f,i
√
= −
−
ω
R
R
R
R 2
gegeben.
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
6
c
°2005
University of Ulm, Othmar Marti
Übungsblatt 07
PHYS 3110 Grundkurs IIIb WH 2004-2005
7
Da Ief f = IE ist, gilt
Ief f =
U
RE
K ·N ·A
√
−
Ief f −
Ief f ω
R
R
R 2
oder
Ief f =
U
R + RE +
K·N
√ ·A ω
2
Damit wird das Drehmoment
2
Mef f (ω) = N AB(Ief f )Ief f = N AKIef
f
Eingesetzt bekommt man
#2
"
Mef f
U
= N AK
R + RE +
K·N
√ ·A ω
2
Dieser Motor hätte, ohne Lagerreibung, eine unendlich grosse maximale Drehzahl. Das Startdrehmoment für ω = 0 ist
·
¸2
U
Mef f (0) = Mmax = N AK
R + RE
2. Die Larmorfrequenz ist
Ω=
e
1.6 · 10−19 C
1
B=
5 · 10−5 T = 4.4 · 106
−31
2me
2 · 9.11 · 10 kg
s
3. Es gibt zwei Zustände für den Spin, parallel und antiparallel zum äusseren
Magnetfeld. Der gesamte Energieunterschied ist dann
¯
¯
¯
~ − (−m
~ ¯¯ = 2mB
∆E = ¯m
~ ·B
~ · B)
Die mittlere Translationsenergie ist
3
Ekin = kT
2
Damit wird
T =
4.
2Ekin
2 · 2mB
4mB
4 · 10−23 J/T · 0.5T
=
=
=
= 0.48K
3k
3k
3k
3 · 1.38 · 10−23 J/K
a) Das elektrische Feld steht senkrecht auf den Platten.
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
7
c
°2005
University of Ulm, Othmar Marti
8
PHYS 3110 Grundkurs IIIb WH 2004-2005
Übungsblatt 07
b) Zu jedem Zeitpunkt ist der Verschiebungsstrom gleich dem aussen fliessenden Strom
IV = 2.0A
c) Mit der Definition des Verschiebungsstromes IV = ²0 dΦdtE erhalten wir
¶
µ
dE
d(AE
1
IV
2.0A
V
dΦE
=
=
· ²0
=
=
= 2.26·1011
−12
2
dt
Adt
²0 A
dt
²0 A
8.85 · 10 F/m · 1m
m·s
d) Der Verschiebungsstrom durch diesen Weg ist proportional zum Flächenverhältnis zu den Kondensatorplatten.
IV0 = IV ·
0.52 m2
= 0.5A
1m2
e)
I
~ · d~s = µ0 I 0 = 1.26 · 10−6 H/m · 0.5A = 6.3 · 10−7 T · m
B
V
5.
a) Wenn eine Spule oder Induktivität an eine Spannung gelegt wird,
fliesst im ersten Augenblick kein Strom. Also ist
I1 = I2 =
U
100V
10
=
= A = 3.33A
R1 + R2
10Ω + 20Ω
3
b) Nach dem genügend lange gewartet wurde, verhält sich L wie ein Kurzschluss. Der Strom I1 ist dann
I1 =
U
100V
100V
100
=
=
=
A = 4.55A
R − 1 + R2 ||R3
10Ω + 20Ω||30Ω
10Ω + 12Ω
22
Der Strom I1 teilt sich auf die beiden Widerstände R2 und R3 umgekehrt proportional zu ihren Werten auf. Also ist
I2 =
k
R2
Wir berechnen
I3 =
µ
I1 = I2 + I3 = k
k
R3
1
1
+
R2 R3
¶
Zusammen
I2 = I1
³
R2
1
1
R2
+
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
1
R3
´ = I1
30Ω
R3
= 4.55A ·
= 2.73A
R2 + R3
20Ω + 30Ω
8
c
°2005
University of Ulm, Othmar Marti
Übungsblatt 07
PHYS 3110 Grundkurs IIIb WH 2004-2005
9
c) Beim Öffnen des Schalters wird der Strom durch R1 sofort zu null
I1 = 0
Der Strom durch L bleibt im ersten Augenblick wie er war (Spule).
Wir haben also
I2 = 4.55A − 2.73A = 1.82A
d) Nach langer Zeit fliesst kein Strom mehr
I1 = I2 = 0
6. Wir verwenden das Faraday-Gesetz
I
~ · d~s = − dΦB
E
dt
auf der Schlaufe. Wir nehmen an, dass am rechten Teilweg das elektrische
Feld null ist, und dass oben und unten das elektrische Feld entweder null
oder senkrecht zum Integrationsweg ist. Damit ist
I
~ · d~s = E · L
E
~ im Inneren des Kondensators
wenn L die Länge der Schlaufe parallel zu E
~ ≡ 0 ist, ist muss auch
ist. Da aber B
I
~ · d~s = 0
E
sein. Damit existiert ein Widerspruch, der nur gelöst werden kann, wenn
~
auf es E-Komponenten
entlang der Teilpfade der Schlaufe gibt, die wir als
null angenommen haben.
~ i entgegengesetzt zu der durch den Umlauf
7. Für beide Wege 1 und 2 ist B
definierten Richtung von d~a.
I
~ · d~s = − dΦB1
E
dt
1
d
=
(B1 · A1 )
dt
dB1
= A1 ·
dt
dB
1
= πr12
dt
= π(0.2m)2 (−0.015T /s)
= −0.00188V
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
9
c
°2005
University of Ulm, Othmar Marti
10
PHYS 3110 Grundkurs IIIb WH 2004-2005
I
Übungsblatt 07
~ · d~s = − dΦB2
E
dt
2
d
=
(B2 · A2 )
dt
dB2
= A2 ·
dt
dB
2
= πr22
dt
= π(0.3m)2 (−0.015T /s)
= −0.00424V
Für den Weg 3 ist der Umlaufsinn gleich wie für den Weg 1. Also ist
I
I
I
~
~
~ · d~s = −0.00188V − (−0.00424V ) = 0.00236V
E · d~s = E · d~s − E
3
1
2
8. Um den 100µF -Kondensator auf 300V aufzuladen benötigt man die Energie
1
1
E1 = CU 2 = · 10−4 F · 3002 V 2 = 4.5J
2
2
Die Anfangsenergie im 900µF -Kondensator ist
1
1
E3 = CU 2 = · 9 · 10−4 F · 1002 V 2 = 4.5J
2
2
Also muss die gesamte Energie vom 900µF -Kondensator auf den 100µF Kondensator übertragen werden. Wir wollen die Energie in der Spule zwischenspeichern. Wenn S1 geschlossen ist und S2 offen ist, bilden C1 und
L einen Schwingkreis. In einem Schwingkreis wird Energie zwischen dem
elektrischen Feld im Kondensator und dem magnetischen Feld in der Spule hin- und hertransferiert (analog zu kinetischer und potentieller Energie
im Pendel). Wenn T1 die Schwingungsdauer des Schwingkreises ist, so ist
nach der Zeit T1 /4 C1 komplett entladen und alle Energie in L. Wenn nun
S1 geöffnet wird und gleichzeitig S2 geschlossen wird, so bilden C2 und L
einen Schwingkreis. Wenn T2 die Schwingungsdauer dieses Schwingkreises
ist, müssen wir T2 /4 warten und alle Energie ist von L auf das elektrische
Feld von C2 übertragen. Wir haben:
p
√
T1 = 2π L · C1 = 2π 10H · 9 · 10−4 F = 0.596s
Also muss S1 während T1 /4 = 0.149s geschlossen sein. Weiter haben wir:
p
√
T2 = 2π L · C2 = 2π 10H · 10−4 F = 0.199s
Also muss S2 für T2 /4 = 0.0497s geschlossen werden. Nun ist C2 auf 300V
aufgeladen.
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
10
c
°2005
University of Ulm, Othmar Marti
Übungsblatt 07
9.
PHYS 3110 Grundkurs IIIb WH 2004-2005
11
a) Die Amplitude des magnetischen Feldes ist
Bm =
Em
5.00V /m
=
= 1.67 · 10−8 T
c
3 · 108 m/s
b) Die Intensität der Welle ist
I =< S >=
2
Em
5.002 V 2 /m2
=
= 0.0331W/m2
−7
8
2µ0 c
2 · 4π · 10 T m/A · 3 · 10 m/s
Übungsblatt vom 7. 2. 2005 oder 14. 2. 2005
11
c
°2005
University of Ulm, Othmar Marti