Messung und Analyse von otoakustischen Emissionen

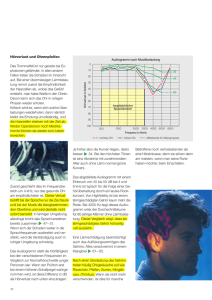
Protokoll zum Versuch im Rahmen des Blockpraktikums
Messung und Analyse von otoakustischen
Emissionen
Oliver Neumann
Sebastian Wilken
Mat.-Nr.: 9134690
Mat.-Nr.: 9150300
10. Juli 2008
1
Einleitung
Dieser Praktikumsversuch im Rahmen des Blockpraktikums Physikalische Messtechnik und digitale Signalver”
arbeitung“ an der Carl von Ossietzky Universität Oldenburg beschäftigt sich mit den otoakustischen Emissionen
(OAE). OAE sind Schallaussendungen des Ohrs, welche erstmals 1978 von David Kemp in [1] beschrieben wurden.
Zunächst werden wir uns im Theorieteil des Protokolls mit dem Aufbau und der Funktionsweise des menschlichen
Ohrs vertraut machen. Danach erläutern wir kurz, was man unter den OAE versteht und welche Klassen dieser
Emissionen existieren. Zum Schluss der theoretischen Behandlung erklären wir einige Begriffe, die grundlegend
für die Untersuchung der OAE sind: Die Nichtlinearität, die Kompression, die Schallausbreitung in der Cochlea
sowie das nichtlineare Aufaddieren.
Im Praktischen Teil werden wir dann verschiedene Messungen von OAE durchführen und an Hand einiger selbst
geschriebener MATLAB-Skripte auswerten.
2
2.1
Theoretischer Teil
Der Aufbau des menschliches Ohrs
In Abbildung 2.1 ist der Aufbau des menschlichen Ohrs mit allen wichtigen Elementen dargestellt. Im Ohr befinden
sich sowohl das Hörorgan, als auch das Gleichgewichtsorgan. Dabei liegt der Hörbereich bei Normalhörenden
zwischen 20 Hz und 20 kHz. Das Hörorgan ist unterteilt in drei Bereiche: Das Außen-, das Mittel- und das Innenohr.
Das Außenohr fasst die Ohrmuschel und den äußeren Gehörgang, der am Trommelfell endet, zusammen. Die
Ohrmuschel dient dazu, die ankommenden Schallwellen aufzufangen. Aufgrund des trichterförmigen Aufbaus des
äußeren Gehörgangs werden die Schallwellen leicht verstärkt. Dann gelangen diese Schallwellen an das Trommelfell
und bringen dieses in Schwingung.
Das Mittelohr definiert den Bereich zwischen dem Trommelfell und dem ovalen runden Fenster. Im Mittelohr
befinden sich die drei Gehörknöchelchen: Hammer, Amboss und Steigbügel. Der Hammer liegt direkt an dem
Trommelfell an und der Steigbügel ist am ovalen Fenster positioniert. Diese beiden Knöchelchen werden durch
den Amboss verbunden. Mit Hilfe dieser drei Gehörknöchelchen werden die Schwingungen verstärkt und vom
Trommelfell auf die Membran des ovalen Fensters übertragen. Außerdem existiert noch eine Ohrtrompete, auch
Eustachische Röhre genannt. Die Eustachische Röhre dient zum Druckausgleich zwischen den beiden Seiten des
Trommelfells.
Das Innenohr besteht einerseits aus einem Konstrukt, das man als Hörschnecke (lat. Cochlea) bezeichnet. Dieses
ist sowohl Teil des Hörorgans, besteht aber auch aus drei Bogengängen und zwei Vorhofsäckchen, die zusammen
1
2
THEORETISCHER TEIL
2
Abbildung 2.1: Aufbau des menschlichen Ohrs, entnommen aus [5].
das Gleichgewichtsorgan bilden. Die Cochlea beginnt an der Basis und endet an der Spitze, auch Apex genannt.
Die Cochlea beinhaltet drei mit Flüssigkeit gefüllte, spiralförmige Kanäle. Der mittlere Kanal wird als Schneckengang deklariert und die beiden umliegenden Kanäle werden als Vorhof- und Paukentreppe bezeichnet. Der
Schneckengang ist von der Paukentreppe durch die Basilarmembran getrennt. Zwischen dem Schneckengang und
der Vorhoftreppe liegt ebenfalls eine Membran, die Reißner-Membran.
Nun werden die Schwingungen von der Membran des ovalen Fensters auf die Flüssigkeit von der Vorhoftreppe
bis zum Apex über ein Schneckenloch in die Paukentreppe, die am runden Fenster endet, weitergeleitet. An der
Basilarmembran befindet sich das Corti-Organ, auf dem sich Haarzellen befinden. Man unterteilt die Haarzellen
in äußere und innere Haarzellen. Die äußeren Haarzellen verstärken die Schallwellen innerhalb der Cochlea. Die
inneren Haarzellen wandeln mechanische Schwingungen in Nervenimpulse um, die dann über den Hörnerv zum
Gehirn gelangen.
2.2
Die otoakustischen Emissionen
Als otoakustische Emissionen (OAE) bezeichnet man akustische Signale, die vom Ohr ausgesendet werden. Die
Ursache hierfür liegt in der nichtlinearen und aktiven Vorverarbeitung in der Cochlea. Erste Anzeichen für die
Nichtlinearität zeigen einige Eigenschaften des Innenohrs, wie zum Beispiel die Frequenzselektierung und der
Dynamikbereich, der thematisch die hohe Empfindlichkeit bei leisen Tönen einschließt. Untersuchungen haben
außerdem gezeigt, dass ein aktiver Mechanismus der Schallausbreitung in der Cochlea zugrunde liegt. Bei diesen Untersuchungen stellte sich heraus, dass die Nichtlinearität des Innenohrs nach dem Tod verschwindet. Des
Weiteren ist es mit Hilfe der OAE möglich, experimentelle Daten vom Innenohr zu gewinnen, ohne dabei direkt
ins Ohr einzudringen. Dabei wird ein empfindliches Mikrofon so in den Gehörgang platziert, dass der Gehörgang
abgeschlossen ist. Die OAE bieten somit eine Möglichkeit, objektive Hörtests durchzuführen, die unabhängig vom
subjektiven Empfinden des Patienten sind.
2.3
Klassifizierung verschiedener OAE-Typen
Die otoakustischen Emissionen werden in drei Klassen unterteilt: Die spontanen otoakustischen Emissionen
(SOAE), die transitorisch evozierten Emissionen (TEOAE) und die Verzerrungsprodukt-Emission (DPOAE, engl.
distortion product emission).
2
THEORETISCHER TEIL
3
Die SOAE sind einzelne sehr leise Töne, die ohne äußeren Reiz vom Ohr ausgesendet werden. Diese Emissionen
liegen in vielen Fällen bei einem niedrigen Schalldruckpegel und bei wenigen Frequenzen vor und sind nur bei
ungefähr der Hälfte aller Normalhörenden nachweisbar. Für den Nachweis der SOAE werden Leistungsspektren der
aufgezeichneten Signale berechnet und gemittelt. Klinisch ist die Untersuchung der SOAE nur von untergeordneter
Bedeutung.
Im Gegensatz zu den SOAE werden bei den TEOAE und bei den DPOAE ein äußerer Reiz ins Ohr gegeben. Bei
den transitorisch evozierten Emissionen wird die Cochlea durch kurze breitbandige Signale, so genannte KlickReize oder -Stimuli, stimuliert. Daraufhin emittiert das Ohr ein breitbandiges Signal mit frequenzabhängiger
Latenz der einzelnen Komponenten. Die emittierten Signale treten zwischen zwei Klick-Reizen auf, d. h., dass der
Stimulus von der Antwort im Zeitbereich getrennt wird. Bei der Verzerrungsprodukt-Emission werden simultan
zwei sinusförmige Impulse ins Ohr gesendet, wobei sich die Signale in der Frequenz unterscheiden. In der Cochlea
werden dann Töne, die sich aus den beiden Impulsen bezüglich der Frequenz kombinieren lassen, so genannte
Kombiantionstöne erzeugt. Bei dieser Art der Emission liegt also eine Trennung des Stimulus und des emittierten Signals im Frequenzbereich vor. Um zufallsbedingtes Rauschen zu minimieren, werden auch bei evozierten
Emissionen die Signalantworten gemittelt.
Die evozierten Emissionen sind bei fast allen Normalhörenden nachweisbar und nehmen von ihrer Bedeutung im
klinischen Bereich zu. Man nutzt unter anderem diese Eigenschaft zur Funktionsprüfung des Innenohrs vor allem
bei Kleinkindern, da sie unabhängig von der Mitarbeit der Kinder bei einem Hörtest ist.
2.4
Wichtige Begriffe
Um einen tieferen Einblick in die otoakustischen Emissionen zu erhalten, werden nun einige Begriffe näher erklärt.
2.4.1
Die Nichtlinearität
Bei nichtlinearen Übertragungsfunktionen stehen Ursache und Wirkung nicht in einem einfachen, linearen Zusammenhang, sondern es liegt eine komplexe, in vielen Fällen exponentielle Beziehung vor. Aus der Nichtlinearität
folgt unter anderem, dass bei einer simultanen Stimulation mit zwei in der Frequenz unterschiedlichen Sinustönen
die so genannten Kombinationstöne auftreten. Die Frequenz der einzelnen Kombinationstöne lassen sich aus einer
Taylorentwicklung herleiten. Man geht in diesem Fall davon aus, dass sich der Schallpegel p wie folgt aus den
beiden Stimulationsfrequenzen zusammensetzt:
p = p1 cos(2πf1 t) + p2 cos(2πf2 t)
(2.1)
Zur weiteren Berechnung sind folgende Additionstheoreme nützlich:
cos(x + y) = cos x − cos y − sin x sin y
cos(x − y) = cos x cos y + sin x sin y
(2.2)
(2.3)
Unter der Verwendung der Gleichungen 2.2 und 2.3 lassen sich für den harmonischen Term der Gleichung 2.1
folgende Kombinationsfrequenzen bestimmen: f2 + f1 , f2 − f1 , 2f1 und 2f2 . Betrachtet man den kubischen Term,
so ergeben sich folgende Frequenzen für die Kombinationstöne: 3f1 , 3f2 , 2f2 + f1 , 2f2 − f1 und 2f1 + f2 sowie
2f1 − f2 .
2.4.2
Kompression
Das menschliche Ohr nimmt einen Schalldruckpegel im Bereich von 0 dB SPL bis 120 dB SPL wahr. Bei der
Umwandlung in Nervenimpulse durch die inneren Haarzellen liegt jedoch nur ein Bereich von maximal 60 dB vor.
Da das Mittelohr die Schallwellen linear vom Trommelfell auf das ovale Fenster überträgt, lässt sich schließen,
dass die Kompression von 120 dB SPL auf maximal 60 dB in der Cochlea stattfinden muss.
2
THEORETISCHER TEIL
2.4.3
4
Schallausbreitung in der Cochlea
Die Basilarmembran ist ein schwingungsfähiges System und lässt sich durch die physikalischen Eigenschaften
Masse, Reibung und Steifigkeit beschreiben. Diese Eigenschaften verändern sich entlang des Corti-Organs. Die
Steifigkeit nimmt von der Basis bis zum Apex hin ab. Das bedeutet, dass dadurch Wanderwellen entstehen und
die maximale Amplitude dieser Wellen in Abhängigkeit der Frequenz an verschiedenen Orten in der Cochlea
vorzufinden ist. Je näher die maximale Amplitude am Apex ist, desto niedriger ist die Frequenz. In der Abbildung
2.2 wird die Verteilung der Wahrnehmungen von Frequenzen in der Cochlea dargestellt.
Abbildung 2.2: Verteilung der Wahrnehmungen von Frequenzen in der Cochlea, entnommen aus [6].
Auch bei den otoakustischen Emissionen entstehen Wanderwellen. Diese Wanderwellen breiten sich von ihrem Ursprung in Richtung des ovalen Fensters aus. Nun werden diese Wellen teilweise transmittiert und der transmittierte
Anteil lässt sich dann im Gehörgang nachweisen.
Im Allgemeinen hängen die mechanischen Eigenschaften von dem Pegel ab, der in der Cochlea vorliegt. Für diese
Abhängigkeit kommen die äußeren Haarzellen in Frage. Man glaubt, dass die äußeren Haarzellen die Steifigkeit
lokal ändern können oder je nach Pegel mehr oder weniger zur Dämpfung beitragen. Es ist sogar möglich, dass
bei einem kleinen Pegel eine Entdämpfung stattfindet, d. h., dass die Wanderwellen verstärkt werden.
2.4.4
Das nichtlineare Aufaddieren
Mit Hilfe des nichtlinearen Aufaddierens ist es möglich, Reizartefakte zu unterdrücken. Bei der Aufzeichnung
überlagern sich die Signalantworten aus dem Innenohr mit den passiven“ Impulsantworten aus dem Gehörgang
”
und Mittelohr. Da die Impulsantworten des Mittelohrs und Gehörganges einen linearen Bezug zum Reizpegel
besitzen, ist es durch das nichtlineare Aufaddieren möglich, die Signalantwort des Innenohrs zu isolieren.
Wir definieren eine Funktion, welche die Intensität des Antwortsignals y in Abhängigkeit zur Intensität des
Stimulus x beschreibt und außerdem einem adaptiven Rauschen mit der Intensität r unterliegt:
y(x) = c1 xm + c2 x + r
(2.4)
Dabei sind c1 , c2 und m positive Konstanten, wobei m bis 1 beschränkt ist. Reizt man beispielsweise nun dreimal mit einem Stimulus der festen Amplitude x und einmal mit der Amplitude −3x und addiert diese nun, so
werden alle linearen Anteile herausgefiltert, die nichtlinearen Anteile jedoch bleiben erhalten. Ein Nachteil des
nichtlinearen Aufaddierens ist es, dass der nichtlineare Anteil in der Frequenz unterschiedlich gewichtet wird. Außerdem werden nichtlineare Verzerrungen des Schallweges nicht herausgefiltert, sondern es wird dem Nutzsignal
zugeordnet und kann bei hohem Reizpegel zu Problemen führen.
3
PRAKTISCHER TEIL
3
5
Praktischer Teil
Im Praktischen Teil werden wir verschiedene Arten von otoakustischen Emissionen mit Hilfe von einer Gehörgangssonde, die mit Miniaturlautsprechern und Mikrofonen ausgestattet ist, aufzeichnen. Dabei werden TEOAE, SOAE
und DPOAE durch verschiedene Stimulationen des Gehörs angeregt und mit entsprechender Software ausgewertet.
3.1
Apparatur
Zur Messung der otoakustischen Emissionen steht ein PC mit zwei Einsteckkarten zur Verfügung, welche die
erforderlichen Mehrkanal-A/D- und -D/A-Wandler beinhalten. Das Signal der bereits angesprochenen Messsonde
wird verstärkt und dann an die Messwerterfassungskarten im PC weitergegeben. Diese Anordnung entspricht
der klinischen Standardapperatur zur Aufzeichnung otoakustischer Emissionen (ILO96 OAE Research System,
Otodynamics Ltd., Hatfield/UK ). Zur Aufnahme der Messdaten wird die Software ILO96 Version 5 verwendet.
Dieses Programm speichert die Daten im Binärsystem ab. Wir verwenden später ein MATLAB-Skript um die Daten
einzulesen und ins ASCII-Format zu konvertieren.
3.2
Aufnahme von TEOAE und SOAE
Wir nehmen nun transitorisch evozierte otoakustische Emissionen (TEOAE) und auch spontane otoakustische
Emissionen (SOAE) auf. Bei der Messung der TEOAE wird die Antwort auf eine Klick-Stimulation gemessen.
Die Daten werden von der Messsoftware binär gespeichert und müssen daher vom bereitgestellten MATLAB-Skript
import ILO.m eingelesen und zur Weiterverarbeitung aufbereitet werden. Die Messsoftware schreibt die aufgenommenen Signale abwechselnd in zwei Puffer, deren Signale nach dem Import in zwei Vektoren gespeichert
werden. In einem weiteren Vektor wird das Zeitsignal des Klick-Stimulus abgespeichert. Es werden ebenfalls noch
die Leistungsdichtespektren (LDS) von Nutz- und Rauschsignal berechnet, welche wir allerdings in der Folge nicht
weiter benötigen. Zur Auswertung und grafischen Darstellung der Signale dient die Funktion einlesen.m:
Listing 1: Quellcode der Funktion einlesen.m.
function [ ] = e i n l e s e n ( f i l e )
[ a , b , s , FS ,FN] = import ILO ( f i l e ) ;
A = fft (a );
B = fft (b ) ;
KLDS = A. ∗ conj (B ) ;
Y = r e a l (KLDS ) ;
f s = 25000;
t = [1/ f s :1/ f s :512/ f s ] ;
f = [ f s /512: f s /512: f s ] ;
maxab = max( abs ( a+b ) ) ;
max AB = max( abs (A+B ) ) ;
figure ;
plot ( t ∗ 1 0 0 0 , ( a+b ) . / maxab ) ;
xlim ( [ 0 , 2 0 ] ) ;
xlabel ( ’ Z e i t / ms ’ ) ;
ylabel ( ’ S c h a l l d r u c k / mPa ’ ) ;
figure ;
plot ( f , 1 0 ∗ log10 (Y. /max(Y ) ) ) ;
xlim ( [ 0 , 6 2 5 0 ] ) ;
xlabel ( ’ Frequenz / Hz ’ ) ;
ylabel ( ’ P e g e l / dB ’ ) ;
wavwrite ( ( 1 / maxab ) ∗ ( a+b ) , f s , 1 6 , ’ o u t f i l e . wav ’ ) ;
3
PRAKTISCHER TEIL
6
Beim Aufruf der Funktion wird die Datei mit den Messdaten als Argument file übergeben. Diese Datei wird
dann mit Hilfe von import ILO.m eingelesen. In den Vektoren a und b befinden sich nun die Puffersignale, in
s der Klick-Stimulus und in FS und FN die Spektren des Nutz- und des Rauschsignals. Nun wird eine FFT der
Puffersignale durchgeführt und in den Vektoren A und B gespeichert. Durch die Operation A.*conj(B) wird
nun das Kreuzleistungsdichtespektrum (KLDS) ermittelt und in KLDS gespeichert. Der Vektor Y enthält den
Realteil des KLDS. Mit Hilfe der bekannten Samplingfrequenz fs werden nun Zeit- und Frequenzvektoren t und
f definiert. Zur späteren Normierung werden noch die Maxima der Beträge von a+b und A+B in den Variablen maxab
bzw. max AB gespeichert. Nun wird die Summe aus beiden Puffern normiert und über der Zeit in ms geplottet.
Anschließend wird ein Plot von Y (in dB) über dem Frequenzvektor f erstellt und wiederum durch Division mit
dem Maximalwert von Y normiert. Des Weiteren wird noch die (normierte) Summe der beiden Puffersignale a
und b mit Hilfe des Befehls wavwrite in eine .wav-Datei geschrieben.
Abbildung 3.1: Zeitsignal für die Messung am Röhrchen mit der Methode des linearen (links) und des nichtlinearen
Aufaddierens (rechts).
Abbildung 3.2: Spektrum für die Messung am Röhrchen mit der Methode des linearen (links) und des nichtlinearen
Aufaddierens (rechts).
Zunächst führen wir einige Testmessungen an einem Kunststoffröhrchen durch, dessen Volumen und Radius in etwa
mit den Ausmaßen des menschlichen Gehörganges übereinstimmen. Bei dem Röhrchen sollten keine otoakustischen
Emissionen zu erwarten sein. Wir benutzen auch hier die Gehörgangsonde, welche wir mit Hilfe eines passenden
Aufsatzes so am Eingang des Röhrchens platzieren, dass es nach außen hin abgeschlossen ist. Es werden nun zwei
3
PRAKTISCHER TEIL
7
Messungen durchgeführt, dabei wird zunächst linear und anschließend nichtlinear aufaddiert. Beim der Methode
des nichtlinearen Aufaddierens der Stimulus dreimal mit einer festen Amplitude x und einmal mit der dreifachen,
umgekehrten Amplitude −3x angeboten. Dadurch können Reizartefakte, die durch die passive Impulsantwort des
Gehörganges entstehen, effektiv unterdrückt werden. Die Abbildungen 3.1 und 3.2 zeigen nun die aufgenommenen
Zeitsignale und Spektren für das Röhrchen für das lineare und das nichtlineare Aufaddieren.
Das Kunststoffröhren ist ein rein passives System. Daher erkennen wir im Zeitsignal für das lineare Aufaddieren
zunächst die passive Impulsantwort des Röhrchens auf den Stimulus. Ab etwa 6 ms nach dem Stimulus ist nur
noch Rauschen zu erkenen. Die Amplitude der Impulsantwort ist im Vergleich zur Amplitude des Rauschens sehr
viel größer. Beim nichtlinaren Aufaddieren hingegen (vgl. Abbildung 3.1, rechts) wird die passive Impulsantwort
soweit wie möglich herausgefiltert. Daher ist nur noch eine sehr kleine Reaktion auf den Stimulus im Zeitsignal
zu erkennen. Ab etwa 5 ms nach dem Stimulus ist nur noch Rauschen zu erkennen, dessen Amplitude hier im
Vergleich zur Reaktion auf den Stimulus viel größer ist. In den entsprechenden Spektren (3.2) ist ebenfalls der
Unterschied zwischen linearem und nichtlinearem Aufaddieren zu erkennen. Beim linearen Fall ist die passive
Impulsantwort auf den Stimulus zwischen 0 kHz und 1 kHz durch ein ausgeprägtes, aufgeweichtes Maximum zu
erkennen. Ab etwa 1 kHz zeigt das Spektrum nur ein breitbandiges Rauschen. Im Spektrum für den Fall des
nichtlinearen Aufaddierens ist nur das Rauschen zu erkennen, die passive Impulsantwort fehlt hier.
Nun führen wir TEOAE-Messungen im Gehöhrgang durch. Dabei untersuchen wir beide Ohren von zwei Versuchspersonen und verwenden jeweils einmal die Methode des linearen und des nichtlinearen Aufaddierens. Wir
beschränken uns bei der weiteren Analyse aber auf die mit dem nichtlinearen Aufaddieren ermittelten Daten. In
den Abbildungen 3.3 und 3.4 sind exemplarisch Zeitsignale und Spektren zweier Messungen dargestellt.
Abbildung 3.3: Zeitsignal und Spektrum für die TEOAE-Messung am linken Ohr der Versuchsperson Sebastian.
Für beide Versuchspersonen ist der für TEOAE typische Verlauf im Zeitsignal zu erkennen. Die Signale sind erst
ab etwa 2,5 ms nach dem Stimulus von Null verschieden, was dadurch zu erklären ist, dass der Schall für den Weg
vom Lautsprecher zur Cochlea und wieder zurück zum Mikrophon eine gewisse Zeit benötigt. Wie wir im Abschnitt
zur Schallausbreitung in der Cochlea gesehen haben, regen die Signalanteile des Stimulus mit hohen Frequenzen
die äußeren Haarzellen nahe dem ovalen Fenster an. Die Signalanteile mit niedrigen Frequenzen hingegen regen
die Haarzellen am Ende der Basilarmembran an. Daher haben die OAE die hier erzeugt werden, einen weiteren
Weg in der Cochlea zurückzulegen und sind später im Zeitsignal zu erkennen. Die zeigen auch unsere Abbildungen
3.3 und 3.4: Das Zeitsignal oszilliert zu kleinen Zeiten am stärksten und die Frequenz der Osziallationen nimmt
mit zunehmender Zeit ab. Die Spektren der TEOAE-Messungen am menschlichen Ohr weisen den erwarteten
breitbandigen Verlauf auf, da die Emissionen mit einem Klicksignal angeregt werden, welches viele Frequenzen
enthält. Im Spektrum für das linke Ohr der Versuchsperson Sebastian ist bei etwa 5,5 kHz ein Peak zu erkennen.
Diese taucht auch in weiteren Messungen auf und stellt wahrscheinlich eine spontane otoakustische Emission dar.
Für ausgewählte TEOAE-Messdaten erstellen wir auch Spektrogramme. Dazu wird in der Funktion einlesen.m
die auf 1 normierten Summe der Signale beiden Puffer in die .wav-Datei outfile.wav geschrieben und im Programm Cool Edit 96 eingelesen. In diesem Programm ist eine Spektrogramm-Funktion enthalten, welche für das
3
PRAKTISCHER TEIL
8
Abbildung 3.4: Zeitsignal und Spektrum für die TEOAE-Messung am rechten Ohr der Versuchsperson Oliver.
Signal ein Diagramm der Frequnenzen über der Zeit erstellt. Ein exemplarisches Spektrogramm (Versuchsperson Sebastian, linkes Ohr) ist in der Abbildung 3.5 dargestellt. Im Spektrogramm sind verschiedene Intensitäten
zu erkennen. Dunkle Bereiche im Zeit-Frequenz-Bereich kommen selten im Signal vor; helle Bereiche kommen
entsprechend häufiger vor. In der Abbildung ist zu erkennen, dass die größten vorkommenden Frequenzen bei
etwa 6,5 kHz liegen. Am häufigsten kommen Frequenzen im Bereich zwischen 0,5 kHz und 5,5 kHz vor. Zwei Frequenzbänder dauern über das gesamte Zeitfenster an. Diese liegen etwa bei 1 kHz und 5,5 kHz. Vermutlich handelt
es sich hier um spontane otoakustische Emissionen, da sie unabhängig von einem Stimulus und dauerhaft von
menschlichen Ohr ausgesendet werden. Die spontane Emission bei 5,5 kHz ist auch im Spektrum (vgl. Abbildung
3.3) zu erkennen.
Abbildung 3.5: Spektrogramm für die TEOAE-Messung am linken Ohr der Versuchsperson Sebastian.
3
PRAKTISCHER TEIL
3.3
9
Pegelabhängigkeit der TEOAE
In diesem Versuchsteil wollen wir die Pegelabhängigkeit der TEOAE untersuchen. Dazu wählen wir eine Testperson
und ein Ohr aus, an der wir alle Messungen durchführen (Hier: Testperson Sebastian, linkes Ohr). Wir beschränken
uns auf die Methode des nichtlinearen Aufaddierens. Der Stimulus wird nun mit verschiedenen Pegeln zwischen
−36 dB und +6 dB dargeboten. Zur Auswertung benutzen wir das Matlab-Skript pegelvar.m. Dieses hat die
Aufgabe, das aufgenommene Spektrum für alle Anregungspegel in ein Diagramm zu plotten. Der Quellcode sieht
im Wesentlichen wie folgt aus:
Listing 2: Quellcode des Skiptes pegelvar.m.
dat = [ ’TEOAE/A1 .DTA ’ ; ’TEOAE/A2 .DTA ’ ; ’TEOAE/A3 .DTA ’ ; ’TEOAE/A4 .DTA ’ ;
’TEOAE/A5 .DTA ’ ; ’TEOAE/A6 .DTA ’ ; ’TEOAE/A9 .DTA ’ ; ’TEOAE/A8 .DTA ’ ] ;
c o l o r s = [ ’ y ’ , ’m’ , ’ c ’ , ’ g ’ , ’ b ’ , ’ k ’ , ’ r ’ , ’ . ’ ] ;
f s = 25000;
t = [1/ f s :1/ f s :512/ f s ] ;
f = [ f s /512: f s /512: f s ] ;
fo r i = 1 : 8
[ a , b , s , FS ,FN] = import ILO ( dat ( i , : ) ) ;
A = fft (a );
B = fft (b ) ;
KLDS = A. ∗ conj (B ) ;
Y( : , i ) = r e a l (KLDS ) ;
end ;
maxy = max(max(Y ) ) ;
fo r i = 1 : 8
plot ( f ( 1 : 1 2 8 ) , 1 0 ∗ log10 (Y( 1 : 1 2 8 , i ) / maxy ) , c o l o r s ( i ) ) ;
hold on ;
end ;
xlim ( [ 0 , 6 2 5 0 ] ) ;
xlabel ( ’ Frequenz / Hz ’ ) ;
ylabel ( ’ P e g e l / db ’ ) ;
Im Vektor dat werden zunächst die Dateinamen für die einzelnen Messungen gespeichert. Mit Hilfe der bekannten
Sampling-Frequenz fs werden wieder Zeit- und Frequenzvektoren t und f erstellt. In einer for-Schleife werden
dann die entsprechenden Dateien mit dem Skript import ILO.m importiert. Die Bezeichnung der Variablen und die
Erstellung des KLDS ist äquivalent zum zuvor besprochenen Skript einlesen.m. Y ist hier aber eine Matrix, in der
jede Spalte das KLDS eines Signals eines bestimmten Anregungspegels entspricht. In einer weiteren for-Schleife
werden schließlich die Spektren für alle acht Anregungspegel geplottet. Zur besseren Unterscheidung wurden zuvor
im Vektor colors verschiedene Farben bzw. Dotierungen für die Graphen gespeichert. Das Diagramm mit den
Spektren ist in Abbildung 3.6 dargestellt.
Aus dem Diagramm wählen wir nun einige Frequenzen aus, an denen alle Graphen lokale Maxima aufweisen.
Wir haben uns hier für die Frequnzen 900 Hz, 1860 Hz, 3420 Hz und 5470 Hz entschieden. Wir berechnen nun,
an welchen Stellen der Matrix Y, in der der Realteil des KLDS gespeichert ist, diese Frequenzen stehen. Für
jede Frequenz x bilden wir nun einen eigenen Vektor fx, in dem die Werte der acht gemessenen Spektren für die
jeweilige Frequenz gespeichert werden. Da die Bestimmung der Maxima nur mit geringer Genauigkeit durchgeführt
werden kann, mitteln wir hier im Bereich von ±2 Samples um die jeweiligen Frequenzen herum. Dann werden die
Vektoren fx über den Anregungspegeln aufgetragen. Die Umsetzung in MATLAB sieht wie folgt aus:
3
PRAKTISCHER TEIL
Abbildung 3.6: Spektren der TEOAE für verschiedene Anregungspegel zwischen -36 dB und +6 dB.
Listing 3: Quellcode zur Erstellung eines Plots des KLDS-Pegels über dem Anregungspegel.
% 900 Hz
fo r i = 1 : 8
f 9 0 0 ( i ) = 10∗ log10 (mean(Y( 1 6 : 2 0 , i ) ) / maxy ) ;
end
% 1860 Hz
fo r i = 1 : 8
f 1 8 6 0 ( i ) = 10∗ log10 (mean(Y( 3 5 : 3 9 , i ) ) / maxy ) ;
end
% 3420 Hz
fo r i = 1 : 8
f 3 4 2 0 ( i ) = 10∗ log10 (mean(Y( 6 8 : 7 2 , i ) ) / maxy ) ;
end
% 5470 Hz
fo r i = 1 : 8
f 5 4 7 0 ( i ) = 10∗ log10 (mean(Y( 1 1 0 : 1 1 4 , i ) ) / maxy ) ;
end
base = (6: −6: −36);
figure ;
plot ( base , f900 , ’ r ’ ,
hold on ;
plot ( base , f1860 , ’ k ’
hold on ;
plot ( base , f3420 , ’ b ’
hold on ;
plot ( base , f5470 , ’ g ’
’ linewidth ’ ,2);
, ’ linewidth ’ ,2);
, ’ linewidth ’ ,2);
, ’ linewidth ’ ,2);
xlabel ( ’ A n r e g u n g s p e g e l / dB ’ ) ;
ylabel ( ’KLDS−P e g e l / dB ’ ) ;
10
3
PRAKTISCHER TEIL
11
Abbildung 3.7 zeigt das entsprechende Diagramm. Es ist zu erkennen, dass das KLDS der gemessenen TEOAESignale mit wachsenden Anregungspegeln des Stimulus ansteigt. Dieser Anstieg verläuft näherungsweise linear.
Durch Ablesen aus der Grafik erhalten wir eine Steigung von etwa 0,6.
Abbildung 3.7: Abhängigkeit des KLDS bei der TEOAE-Messung vom Anregungspegel des Stimulus.
3.4
Messung von DPOAE
Auf Grund der im Theorieteil näher beschriebenen Nichtlinearität der Schallverarbeitung entstehen im Gehör
Kombinationstöne, wenn man als Stimulus zwei Sinustöne unterschiedlicher Frequenz darbietet. Diese bezeichnet
man als Verzerrungsprodukt-Emissionen (DPOAE). Zur Messung dieser DPOAE benutzen wir wieder die oben
beschriebene Apparatur und Software. Dabei werden die beiden Primärtöne über zwei separate Lautsprecher in
den Gehörgang abgestrahlt und die resultierende Antwort von einem Mikrophon aufgezeichnet. Zunächst nehmen
wir für das Plastikröhrchen und die Versuchsperson Sebastian DPOAE-Spektren auf. Dazu arbeiten wir mit den
Primärtonfrequenzen f1 = 2000 Hz und f2 = 2200 Hz, was einem Primärtonverhältnis von f2 /f1 = 1,2 entspricht.
Die Primärtöne sind symmetrisch angeordnet und ihr Pegel beträgt 60 dB. Wir betrachten jeweils das Spektrum
in einem Bereich zwischen 1400 Hz und 2400 Hz. Dazu lesen wir die Pegel der Primär- und Kombinationstöne
sowie der beiden Rauschsignale 1sp und 2sp aus den Messdateien aus und stellen sie in MATLAB dar. Auf die
Angabe des Quellcodes verzichten wir hier auf Grund der Übersichtlichkeit.
Die Abbildung 3.8 zeigt vier ausgewählte DPOAE-Spektren. Im Abbildungsteil (a) ist die Messung für das Plastikröhrchen dargestellt. Hier werden erwartungsgemäß alle Kombinationstöne vom Rauschen maskiert, da das
Rohr keine Nichtlinearität aufweist. Die Teilabbildungen (b) bis (d) zeigen verschiedene Messdurchläufe am linken Ohr der Versuchsperson Sebastian. Hier setzen sich die Kombinationstöne unterschiedlich gut vom Rauschen
ab. Die Tatsache, dass einige Kombinationstöne deutlich über den Rauschsignalen liegen, weist darauf hin, dass
die Versuchsperson eine ausgeprägte Nichtlinearität in der Schallverarbeitung zeigt und somit normalhörend ist.
Die Teilabblidung (d) zeigt das beste Ergebnis, da sich hier alle aufgenommenen Kombinationstöne (2f1 − f2 ,
2f2 − f1 , 3f1 − 2f2 , 4f1 − 3f2 ) deutlich vom Rauschen absetzen.
Nun erstellen wir für das linke Ohr der Testperson Sebastian so genannte DP-Gramme. Dabei bleibt das
Primärtonverhältnis konstant bei f2 /f1 = 1,2 und die Frequenz f2 wird schrittweise in verschiedenen Bereichen variiert. Man betrachtet nun den Pegel des kubischen Differenztones 2f1 − f2 , da dieser im Allgemeinen am
wenigsten vom Rauschen maskiert wird. Dieser Pegel wird nun über den verschiedenen betrachteten Frequenzen
f2 aufgetragen. In der Abbildung 3.9 ist dies exemplarisch für die beiden Frequenzbereiche 1200 Hz bis 2400 Hz
und 2400 Hz bis 4800 Hz dargestellt. Dabei wurden die Grafiken wieder mit MATLAB erstellt und die beiden Rauschsignale 1sp und 2sp eingezeichnet. In beiden Teilabbildungen ist zu erkennen, dass sich der kubische Differenzton
LITERATUR
12
bei allen betrachteten Frequenzen f2 deutlich vom Rauschen absetzt. Man kann daher davon ausgehen, dass die
Versuchsperson im kompletten betrachteten Frequenzbereich normalhörend ist. Allerdings zeigen die Grafiken,
dass der Pegel des kubischen Differenztones im Frequenzbereich zwischen 2400 Hz bis 4800 Hz mit etwa 5 dB SPL
unterhalb des Pegels im Frequenzbereich zwischen 1200 Hz bis 2400 Hz von durchschnittlich etwa 8 dB SPL liegt.
Der Unterschied zwischen dem Rauschen und dem DP-Gramm-Signal beträgt in beiden Fällen etwa 15 dB SPL
bis 20 dB SPL.
Literatur
[1] D. T. Kemp: Stimulated acoustic emissions from within the human auditory system. Journal of the Acoustical
Society of America, 64(5), Nov. 1978.
[2] Volker Hohmann u. a.: Blockpraktikum Physikalische Messtechnik und digitale Signalverarbeitung“. An”
leitung für das Praktikum an der Carl von Ossietzky Universität Oldenburg in WiSe 2007/2008.
[3] Birger Kollmeier: Audiologie. Skript zur Vorlesung an der Carl von Ossietzky Universität Oldenburg.
[4] H. Gobsch: Otoakustische Emissionen – Grundlagen und klinische Anwendung. Vortrag an der Klinik für
Hals-, Nasen- und Ohrenheilkunde Plastische Operationen HELIOS Klinikum Erfurt.
[5] Internetseite Das Gehör. Stand: 16. April 2008.
URL: http://www.airflag.com/Hirn/w4/w4sinne-Dateien/ohr.jpg
[6] Internetseite Das Gehör. Stand: 16. April 2008. URL: http://ces.univ-karlsruhe.de/∼feldbusch/
InfoverarbLw/Ausarbeitung/Das menschliche Ohr Teil 1.pdf
[7] Internetseite Basics of OAEs – Distortion product otoacoustic emissions. Stand: 9. Juli 2008.
URL: http://www.otoemissions.org/definitions/DPOAE.html
[8] Internetseite Fallbeispiele zur Anwendung von OAE. Stand: 9. Juli 2008.
URL: http://www.buchhandel.de/WebApi1/GetMmo.asp?MmoId=3134557&mmoType=PDF
LITERATUR
13
Abbildung 3.8: Aufgenommene Spektren für die Messung von DPOAE für ein Plastikröhrchen [(a)] und die
Versuchsperson Sebastian [(b) bis (d)] bei einem Primärtonverhältnis von f2 /f1 = 1,2.
Abbildung 3.9: DP-Gramme für zwei verschiedene Frequenzbereiche von f2 für das linke Ohr der Versuchsperson
Sebastian. Das Primärtonverhältnis beträgt hier f2 /f1 = 1,2.