Mikroökonomie Externalitäten Übersicht

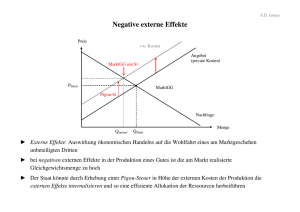
Mikroökonomie
Externalitäten
Universität Erfurt
Wintersemester 08/09
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
1 / 44
Winter
2 / 44
Übersicht
Externalitäten
Korrekturmöglichkeiten für Marktversagen
Ressourcen im Gemeineigentum
stellungsabhängige Externalitäten
Prof. Dittrich (Universität Erfurt)
Externalitäten
Negative Externalitäten
Kosten (Nutzenminderung) einer Partei, die durch Handlungen einer
anderen Partei entstehen.
Umweltverschmutzung
Passiv-Rauchen
Laute Party beim Nachbarn
Positive Externalitäten
Gewinn (Nutzensteigerung) einer Partei, die durch Handlungen einer
anderen Partei entstehen.
Impfungen
Ausbildung
I
I
I
I
Steigert Partizipationsrate bei Wahlen
Reduziert die Kriminalitätsneigung (mehr als eine
Einkommenssteigerung)
Verringert die Abhängigkeit von Sozialhilfe
Steigert die Arbeitsproduktivität und das Wirtschaftswachstum
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
3 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Ronald H Coase, “The Problem of Social Cost”, Journal of Law and Economics, 3, 1960, pp.144–171.
Ein Arzt wird durch den Lärm einer lauten Maschine eines
benachbarten Zuckerbäckers so gestört, dass er nicht arbeiten kann
Ohne die Maschine kann der Zuckerbäcker nicht arbeiten
Nutzen des Zuckerbäckers aus der Maschine: 40
Nutzen des Arztes, wenn er arbeiten kann: 60
Rechtl. Situation
Ergebnis
Z haftbar
Z schließt
Arzt zahlt P, damit
Z schließt
Z nicht haftbar
Prof. Dittrich (Universität Erfurt)
Arzt
Nettonutzen
Zuckerbäcker
Total
60
0
60
60-P
P
60
Externalitäten
Winter
4 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Nutzen des Zuckerbäckers aus der Maschine: 60
Nutzen des Arztes, wenn er arbeiten kann: 40
Rechtl. Situation
Ergebnis
Z haftbar
Z nicht haftbar
Z zahlt 40 an A
A schließt
Arzt
Nettonutzen
Zuckerbäcker
Total
40
0
20
60
60
60
Die Partei mit dem geringeren Nutzen schließt.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
5 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Nutzen des Zuckerbäckers aus der Maschine: 40
Kosten eines Lärmschutzes für den Zuckerbäcker: 20
Nutzen des Arztes, wenn er arbeiten kann: 60
Rechtl. Situation
Z haftbar
Z nicht haftbar
Ergebnis
Z installiert
Lärmschutz auf
eigene Kosten
A zahlt
20 ≤ P ≤ 60, damit
Z Lärmschutz
installiert
Prof. Dittrich (Universität Erfurt)
Arzt
Nettonutzen
Zuckerbäcker
Total
60
20
80
60-P
20+P
80
Externalitäten
Winter
6 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Nutzen des Zuckerbäckers aus der Maschine: 40
Kosten eines Lärmschutzes für den Zuckerbäcker: 20
Nutzen des Arztes, wenn er arbeiten kann: 60
Arzt kann Praxis in ein anderes Zimmer verlegen, Kosten: 18
Rechtl. Situation
Z haftbar
Z nicht haftbar
Ergebnis
Z zahlt
18 ≤ P ≤ 20 an A,
damit er umzieht
A zieht auf eigene
Kosten um
Prof. Dittrich (Universität Erfurt)
Arzt
Nettonutzen
Zuckerbäcker
Total
42+P
40-P
82
42
40
82
Externalitäten
Winter
7 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Nutzen des Zuckerbäckers aus der Maschine: 60
Kosten eines Lärmschutzes für den Zuckerbäcker: 20
Nutzen des Arztes, wenn er arbeiten kann: 40
Verhandlungskosten: 25
Rechtl. Situation
Z haftbar
Z nicht haftbar
Ergebnis
Z installiert
Lärmschutz auf
eigene Kosten
A schließt
Prof. Dittrich (Universität Erfurt)
Arzt
Nettonutzen
Zuckerbäcker
Total
40
40
80
0
60
60
Externalitäten
Winter
8 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Nutzen des Zuckerbäckers aus der Maschine: 60
Nutzen des Arztes, wenn er arbeiten kann: 40
Arzt kann Praxis in ein anderes Zimmer verlegen, Kosten: 18
Verhandlungskosten: 25
Rechtl. Situation
Ergebnis
Z haftbar
Z zahlt 40
A zieht auf eigene
Kosten um
Z nicht haftbar
Prof. Dittrich (Universität Erfurt)
Arzt
Nettonutzen
Zuckerbäcker
Total
40
20
60
22
60
82
Externalitäten
Winter
9 / 44
Externalitäten
Der Zuckerbäcker und der Arzt
Ohne Verhandlungskosten
Die Parteien erreichen eine effiziente Löseung
Mit (hohen) Verhandlungskosten
Es hängt von der rechtlichen Situation und den Handlungsoptionen
der Parteien ab, ob eine effiziente Lösung erreicht wird.
Coase Theorem
Wenn durch Externalitäten betroffene Parteien ohne Verhandlungskosten
miteinander verhandeln können, werden sie eine effiziente Lösung erreichen
– unabhängig von der Ausgestaltung der (handelbaren) Rechte.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
10 / 44
Externalitäten und Effizienz
Externe Kosten
Szenario
Papierwerke leitet Abwässer in einen Fluss ein.
Die Abwässer des gesamten Papiermarktes können durch eine
Reduzierung der Gütermenge gesenkt werden (Produktionsfunktion
mit festem Einsatzverhältnis).
Die externen Grenzkosten (MEC) sind die den flussabwärts
arbeitenden Fischern bei jedem Produktionsniveau entstehenden
Kosten.
Die gesellschaftlichen Grenzkosten (MSC) sind die Summe der
Grenzkosten (MC) und der externen Grenzkosten (MEC).
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
11 / 44
Externalitäten und Effizienz
MSC
Preis
Preis
MSCI
MC
S = MCI
Gesellschaftliche
Gesamtkosten der
negativen
Externalität
P*
P1
P1
MECI
MEC
D
q* q1
Unternehmens
-output
Q* Q1
Branchenoutput
Bestehen negative Externalitäten, sind die gesellschaftlichen Grenzkosten
(MSC) höher als die Grenzkosten.
Die Differenzen sind gleich den externen Grenzkosten (MEC).
Ein gewinnmaximierendes Unternehmen produziert in q1 , während die
effiziente Produktionsmenge bei q∗ liegt.
Der kompetitive Branchenoutput liegt bei Q1 , während das effiziente
Produktionsniveau bei Q∗ liegt.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
12 / 44
Externalitäten und Effizienz
MSC
Preis
Preis
MSCI
MC
S = MCI
Gesellschaftliche
Gesamtkosten der
negativen
Externalität
P*
P1
P1
MECI
MEC
D
q* q1
Unternehmens
-output
Q* Q1
Branchenoutput
Das Marktgleichgewicht bei vollkommenen Wettbewerb maximiert die
Summe der Konsumentenrente und Produzentenrente.
Aufgrund negativer Externalitäten wird jedoch die Wohlfahrt nicht
maximiert.
Im vollkommenen Wettbewerb wird zu viel Verschmutzung produziert, weil
die Firmen die Kosten der Verschmutzung nicht tragen.
Der Wohlfahrtsverlust entsteht, weil der Markt das Gleichgewicht mit den
Grenzkosten der Produktion und nicht mit den gesellschaftlichen
Grenzkosten herstellt.
Die Wohlfahrt im sozialen Optimum ist höher, weil der Gewinn durch
weniger Verschmutzung den Verlust durch weniger Produktion übersteigt.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
13 / 44
Externalitäten und Effizienz
Unter vollkommenen Wettbewerb werden zu viele negative externe
Effekte produziert, weil die Produzenten nur ihre privaten Kosten und
nicht die (höheren) gesellschaftlichen Kosten tragen müssen.
Im sozialen Optimum gibt es ein positives Level von
Umweltverschmutzung.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
14 / 44
Winter
15 / 44
Die Algebra der Externalitäten
Das Gewinnmaximierungsproblem des Papierwerks lautet
max pp x − cp (x , d)
x ,d
und der Fischerei
max pf f − cf (f , d)
f
Bedingungen für die Gewinnmaximierung des Papierwerks
∂cp (x ∗ , d ∗ )
∂x
∂cp (x ∗ , d ∗ )
0=
∂d
pp =
und für die Fischerei
pf =
∂cf (f ∗ , d ∗ )
∂f
Prof. Dittrich (Universität Erfurt)
Externalitäten
Die Algebra der Externalitäten
P
MC (d)
f
Es wird soviel verschmutzt bis
∂cp (x ∗ , d ∗ )
=0
∂d
MCp (x ∗ , d ∗ ) = 0
d
MC p(d)
Die Fischerei hat keinen Einfluß auf die Verschmutzungsmenge
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
16 / 44
Die Algebra der Externalitäten
Pareto-effizienter Produktionsplan für Papier und Fisch:
Internalisierung der negativen Externalität
Das Gewinnmaximierungsproblem der fusionierten Unternehmung lautet
max pp x + pf f − cp (x , d) − cf (f , d)
x ,f ,d
Bedingungen für die Gewinnmaximierung
∂cf (f˜, d̃)
∂cp (x̃ , d̃)
pf =
∂x
∂f
∂cp (x̃ , d̃) ∂cf (f˜, d̃)
0=
+
∂d
∂d
pp =
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
17 / 44
Die Algebra der Externalitäten
Pareto-effizienter Produktionsplan für Papier und Fisch:
Internalisierung der negativen Externalität
P
−MCp (d)
Im Pareto-Optimum wird soviel
verschmutzt bis
MC (d)
f
∂cp (x ∗ , d ∗ )
∂cf (x̃ , d̃)
=
∂d
∂d
−MCp (x̃ , d̃) = MCf (f˜, d̃) > 0
~
d
−
d
MC p(d)
Durch Internalisierung der Externalität wird soviel verschmutzt bis Grenznutzen
aus Verschmutzung gleich Grenzkosten aus Verschmutzung ist.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
18 / 44
Externalitäten und Effizienz
Positive Externalitäten und Ineffizienz
Externalitäten können auch zu einem zu niedrigen Produktionsniveau führen.
Beispiel: Bildung und Studiengebühren
Wert
MSB
D
P1
MC
P*
MEB
q1
q*
Prof. Dittrich (Universität Erfurt)
Bildungsniveau
Externalitäten
Bestehen positive Externalitäten,
ist der gesellschaftliche
Grenznutzen höher (MSB) als der
Grenznutzen D.
Ein eigennütziger Student investiert
q1 in seine Ausbildung. Das
effiziente Bildungsniveau q ∗ liegt
höher. Durch den höheren Preis P1
wird der Student von zusätzlicher
Bildung abgehalten.
Winter
19 / 44
Auswege aus der Ineffizienz
Regulierung und Internalisierung von Externalitäten
Regulierung: Festschreibung einer Verschmutzungsobergrenze für
jedes Unternehmen, so dass die Summe das sozial optimale
Outputlevel ergibt.
Unternehmen erhalten handelbare Zertifikate, die zur Verschmutzung
berechtigen, wobei die Summe der Rechte dem sozialen Optimum
entspricht.
Besteuerung des Verhaltens, das zu negativen externen Effekten führt
(Pigou Steuer)
Verleihung von Eigentumsrechten (Coase)
Probleme der staatlichen Intervention:
Regulierung, Zertifikate, Besteuerung: Der Staat hat in der Regel
nicht genügend Information, um das soziale Optimum zu bestimmen
Bei technologischem Fortschritt gibt es keine Anreize für die
Produzenten weniger Verschmutzung zu produzieren.
Eigentumsrechte: Transaktionskosten
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
20 / 44
Auswege aus der Ineffizienz
Internalisierung von Externalitäten: Pigou-Steuern
Pigou-Steuern sind staatliche festgelegte Preise für die Produktion
eines externen Effekts.
Pigou-Steuern erhöhen die Effizienz
Die gesellschaftlichen Grenzkosten der Verschmutzung und damit das
optimale Verschmutzungsniveau müssen bekannt sein
y Dann kann aber auch direkt die Verschmutzungsmenge reguliert
werden...
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
21 / 44
Don’t Drink and Drive
Alkoholisierte Autofahrer haben eine 7 - 13 mal so hohe
Wahrscheinlichkeit einen tödlichen Autounfall zu verursachen als
nüchterne Autofahrer
Betrunkene akzeptieren das persönliche Risiko, aber sie verursachen
auch negative Externalitäten: mindestens 30 Cent pro gefahrene Meile
Um die gesellschaftlichen Kosten zu internalisieren ist eine Strafe von
mindestens 8000 US Dollar nötig
Levitt, Porter, “How Dangerous Are Drinking Drivers?”, Journal of Political
Economy, 2001, 109(6), pp. 1198-237
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
22 / 44
Figure
18.1 Welfare
Effects ofFigure 18.2 Taxes to Control Pollution
Auswege
aus der Ineffizienz
Internalisierung
von Externalitäten:Market
Pigou-Steuern
Pollution
in a Competitive
Das
Gewinnmaximierungsproblem des Papierwerks lautet
max pp x − cp (x , d) − τ d
© 2007 Pearson Addison-Wesley. All rights reserved.
18–2
x ,d
© 2007 Pearson Addison-Wesley. All rights reserved.
18–1
Figure 18.2 Taxes to Control
Pollution. Placing a tax on the firms equal to the harm
g, causes them to internalize the externality, so their private
Bedingungen für die Gewinnmaximierung
des= MC
Papierwerks
from the gunk, t(Q)
marginal cost is the same as the social marginal cost, MCs. As a result, the
Figure 18.1 Welfare Effects of Pollution
∗
∂c (x ∗ , in
d ∗a)Competitive Market.∂cThe(xcompetitive
, d ∗)
p
p equilibrium is the same as the social optimum, es. Alternatively,
competitive after-tax
pp =
0 =curve
− and the
equilibrium, ec, is determined
by the intersection of the demand
∂x
competitive supply or private marginal cost curve,
MCp,
−τ
applying a specific ∂d
tax of = $84 per ton of paper, which is the marginal harm from the
whichatignores
of in the social optimum.
gunk
Qs = 84,the
alsocost
results
pollution. The social Prof.
optimum,
, is at the Erfurt)
intersection of the demand
curve and the
Dittriches(Universität
Externalitäten
Winter
23 / 44
social marginal cost curve, MCs = MCp + MCg, where MCg is the marginal cost of the
Auswege aus der Ineffizienz
pollution (gunk). Private producer surplus is based on the MCp curve,and social
producer surplus is based on the MCs curve.
Internalisierung von Externalitäten: Pigou-Steuern
Wenn die Pigou Steuer den Grenzkosten der Verschmutzung entspricht
τ=
∂cf (x̃ , d̃)
∂d
dann erreicht man das Pareto-optimale Verschmutzungsniveau, da dann
τ=
∂cf (x̃ , d̃)
∂cp (x ∗ , d ∗ )
∂cp (x̃ , d̃)
=
−
=−
© 2007 Pearson Addison-Wesley.
∂d
∂d
∂d
18-2
die Steuer gleich den Grenzkosten der Verschmutzung, gleich dem
Grenznutzen aus Verschmutzung ist.
© 2007 Pearson Addison-Wesley.
18-1
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
24 / 44
Auswege aus der Ineffizienz
Internalisierung von Externalitäten: Eigentumsrechte
Die Fischerei besitze das Recht auf sauberes Wasser, und das Recht
“Verschmutzung” verkaufen zu können.
Der Preis je Verschmutzungeinheit sei q.
Das Gewinnmaximierungsproblem des Papierwerks lautet
max pp x − cp (x , d) − qd
x ,d
und der Fischerei
max pf f − cf (f , d) + qd
f ,d
Die Gewinnmaximierungbedingungen sind
∂cf (f ∗ , d ∗ )
∂f
∂cf (f ∗ , d ∗ )
q=
∂d
∂cp (x ∗ , d ∗ )
∂x
∂cp (x ∗ , d ∗ )
q=−
∂d
pf =
pp =
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
25 / 44
Auswege aus der Ineffizienz
Internalisierung von Externalitäten: Eigentumsrechte
Die Fischerei besitze das Recht auf sauberes Wasser, und das Recht
“Verschmutzung” verkaufen zu können.
q=−
∂cp (x ∗ , d ∗ )
∂d
q=
∂cf (f ∗ , d ∗ )
∂d
impliziert
−
∂cp (x ∗ , d ∗ )
∂cf (f ∗ , d ∗ )
=
.
∂d
∂d
Damit sind wieder Grenznutzen aus Verschmutzen gleich Grenzkosten aus
Verschmutzung.
Jedes Unternehmen ist mit den sozialen Grenzkosten seiner Handlungen
konfrontiert.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
26 / 44
Auswege aus der Ineffizienz
Internalisierung von Externalitäten: Eigentumsrechte
Das Papierwerk besitze das Recht auf “Verschmutzung” bis zu einem Maximum d̄
und kann Verschmutzungseinheiten zum Preis q verkaufen.
Das Gewinnmaximierungsproblem des Papierwerks lautet
max pp x − cp (x , d) + q(d̄ − d)
x ,d
und der Fischerei
max pf f − cf (f , d) − q(d̄ − d)
f ,d
Die Gewinnmaximierungbedingungen sind
∂cf (f ∗ , d ∗ )
∂f
∂cf (f ∗ , d ∗ )
q=
∂d
∂cp (x ∗ , d ∗ )
∂x
∂cp (x ∗ , d ∗ )
q=−
∂d
pp =
Prof. Dittrich (Universität Erfurt)
pf =
Externalitäten
Winter
27 / 44
Externalitäten und Effizienz im Monopol
Im vollkommenen Wettbewerb werden immer zu viele negative
Externalitäten produziert
Im Monopol ist das nicht notwendigerweise der Fall.
Im Monopol kann das Problem auch nicht durch Internalisierung der
Externalität mithilfe einer Steuer gelöst werden.
Ob im Monopol mehr, genausoviel oder weniger als im sozialen
Optimum produziert wird, hängt von der Nachfragelastiziät und der
Stärke der negativen Externalität ab.
Bei Existenz von Externalitäten kann die Wohlfahrt im Monopol
größer sein als unter vollkommenen Wettbewerb
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
28 / 44
Externalitäten und Effizienz im Monopol
P, $ per ton
450
MC s = MC p + MC g
et
330
310
282
em
A
B
es
C
MC p
D
ec
240
MC g
30
0
MR
60 70
Prof. Dittrich (Universität Erfurt)
84
105
Demand
225
Q, Tons of paper per day
Externalitäten
Winter
29 / 44
Ressourcen im Gemeineigentum
Jedermann hat freien Zugriff auf derartige Ressourcen.
Folglich ergibt sich oft eine Übernutzung.
Beispiele
I
I
I
Luft und Wasser
Fisch- und Tierbestände
Bodenschätze
100 Fischer können entweder im Ozean oder in einem kleinen See
fischen: 100 = Xo + Xs
Im Ozean fängt jeder Fischer 50 Fische: Yo = 50Xo
Im See ist die Anzahl der gefangenen Fische pro Fischer abhängig von
der Anzahl der Fischer, insgesamt fangen sie: Ys = 90Xs − Xs2
Jeder Fischer wählt den Ort aus, an dem er die meisten Fische fängt.
Im Gleichgewicht wird jeder Fischer auf dem Ozean und auf dem See
die gleiche Anzahl an Fischen fangen:
Yo
Ys
=
Xo
Xs
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
30 / 44
Ressourcen im Gemeineigentum
50Xo
90Xs − Xs2
=
Xo
Xs
50 = 90 − Xs
Xs = 40
Xo = 60
Die Fischer fangen also
Ys = 3600 − 1600 = 2000
Y = 5000
Yo = 50 × 60 = 3000
Ist das effizient?
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
31 / 44
Ressourcen im Gemeineigentum
Angenommen, die Fischer sind in einer großen Firma eingestellt, die den Einsatz
zentral plant:
Y = 50Xo + 90Xs − Xs2
100 = Xs + Xo
Y = 50(100 − Xs ) + 90Xs − Xs2
= 5000 − 40Xs − Xs2
∂Y
= 40 − 2Xs = 0
∂Xs
Xs = 20
Xo = 80
Die Fischer fangen also
Ys = 90 × 20 − 400 = 1400
Yo = 80 × 50 = 4000
Y = 5400
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
32 / 44
Ressourcen im Gemeineigentum
Kosten,
Nutzen
(Euro pro
Fisch)
Ohne Kontrollen ist die
Fischmenge/ Monat gleich FC ,
wobei gilt MPC = MB.
Gesellschaftliche
Grenzkosten
Private Grenzkosten
Nachfrage
F*
FC
Prof. Dittrich (Universität Erfurt)
Fischmenge pro Monat
Externalitäten
Allerdings untertreiben die
privaten Kosten die
tatsächlichen Kosten. Das
effiziente Niveau der
Fischmenge/ Monat ist gleich
F*, wobei gilt MSC = MB.
Winter
33 / 44
Ressourcen im Gemeineigentum
Öffentliche Resourcen, bei denen Rivalität im Verbrauch aber
Nichtausschließbarkeit der Konsumenten (Produzenten) gilt, werden oft zu stark
genutzt, da jeder nur seine privaten Kosten berücksichtigt (Tragödie der
Allmende).
Lösung:
Privateigentum (Schaffung der Ausschließbarkeit)
Zentrale Planung (Planer muß alles wissen)
Zertifikate (Der Staat muß die optimalen Mengen kennen)
Pigou-Steuer
Yo
= 50
Xo
50 = 90 − Xs − t
Ys
= 90 − Xs − t
Xs
→ t = 20
Die optimale Pigou-Steuer ist gleich den zusätzlichen Kosten der
Gesellschaft. Der Staat muß diese Kosten kennen.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
34 / 44
stellungsabhängige Externaliäten
Häufig ist nicht die absolute Leistung sondern die relative Leistung
wichtig
Beispiel: Sportwettbewerbe, politische Wahlen, militärische
Vormachtstellung
Wenn A und B um einen Preis kämpfen, mindert jede für A
vorteilhafte Aktion die Chancen von B
Aber: Wenn alle Radfahrer dopen hat kein Radfahrer einen Vorteil aus
der Nutzung leistungssteigernder Drogen
stellungsabhängige Externalitäten führen zu kostspieligem
“Wettrüsten”
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
35 / 44
Status-Streben
In einer Ökonomie leben n Individuen.
Ihre Ausgaben für Kleidung (Auto, Haus, Schmuck) seien xi . Im
Durchschnitt geben sie x̂ aus.
Der Nutzen jedes Individuums sei: Ui = −δ(x̂ − xi ) − αxi2 + βxi
FOC:
∂Ui
∂xi
= β + δ − 2αxi = 0
Da alle Individuen identisch sind, konsumieren sie xi =
Maximiert dies die Wohlfahrt?
Prof. Dittrich (Universität Erfurt)
Externalitäten
β+δ
2α
Winter
36 / 44
Status-Streben
Die Wohlfahrt sei die Summe der Individualnutzen
n
X
i
FOC:
Ui = n[−δ(x − x ) − αx 2 + βx = n(−αx 2 + βx )
∂W
∂x
= −n(2αx + β)
Der wohlfahrtsoptimale Konsum ist also
x1∗ = x2∗ = · · · = xn∗ =
β
2α
Die Konsumentscheidung unter Status-Streben ist größer als der
β
∗
sozial optimale Konsum. xi = β+δ
2α > 2α = xi
Das Streben nach Status führt zu einem ineffizienten Ergebnis.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
37 / 44
Geschenke vs. Geld
Waldvogel (1993), The Deadweightloss of Christmas, American Economic Revue 83, pp. 1328–1336
Geber
Wert
Preis $
Ausbeute (%)
Bargeld (%)
Tante
Bruder
Eltern
Partner
Großeltern
Freunde
40.5
23.5
133.3
24.1
56.1
22.1
64.6
28.3
135.6
25.4
75.9
25.3
64.4
86.2
86.5
91.7
62.9
98.8
14.3
5.8
9.6
0.0
42.3
6.1
77.6
84.0
83.9
11.5
Gesamt
Warum beschenkt man sich, wenn man weiß, dass das Geschenk dem
Beschenkten weniger wert ist als es kostet?
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
38 / 44
Geschenke geben und erhalten
Angenommen, in einer Ökonomie gebe es λ Güter und n
Konsumenten.
Der individuelle Nutzen setzt sich zusammen aus zwei Substituten,
dem Nutzen aus dem Erhalt eines Geschenks ViR , und dem Nutzen
aus dem selber Schenken ViG .
Jeder Konsument mag eines der λ Güter besonders und misst ihm den
Wert β zu, alle anderen Güter werden nur mit β − δ bewertet.
ViR (j)
=
(
β
β−δ
Prof. Dittrich (Universität Erfurt)
wenn j = i
wenn j =
6 i
Externalitäten
Winter
39 / 44
Geschenke geben und erhalten
Da es λ Güter gibt, ist der Erwartungsnutzen aus einem Geschenk
EViR =
λ−1
λ−1
1
β+
(β − δ) = β −
δ
λ
λ
λ
Zum Geschenkgeber...
Jedes Gut koste p.
Es gibt einen sozialen Druck (Externalität), ein Geschenk mit einem
Geschenk zu erwidern. Schenkt der Beschenkte nichts erleidet er einen
negativen Nutzen γ.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
40 / 44
Geschenke geben und erhalten
Der Nutzen eines Geschenkgebers aus Schenken ist also

0
wenn er nicht beschenkt wurde





und selbst nichts schenkt



−p wenn er selbst beschenkt wurde
ViG =

und dann etwas schenkt





−γ
wenn
er selbst beschenkt wurde



und dann nichts schenkt
Annahme: Der soziale Leidensdruck ist größer als die Kosten für ein
Geschenk: γ > p
Folgerungen:
1
2
Jedes Individuum, welches ein Geschenk erhält, schenkt selbst
Jedes Individuum, welches kein Geschenk erhält, schenkt selbst nichts
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
41 / 44
Geschenke geben und erhalten
Alle n Konsumenten schenken jedem anderen etwas (kaufen also n − 1
Geschenke).
Der Erwartungnutzen daraus ist:
EUi = (n −
1)(EViR
+
ViG )
λ−1
= (n − 1) β −
δ−p
λ
Wenn niemand jemand anderem etwas schenkt und sein Geld für das am
meisten bevorzugte Gut ausgibt gilt
Ui = (n − 1)(β − p)
Jedes Individuum hat einen größeren Nutzen in einer Ökonomie in der keine
Geschenke ausgetauscht werden als in einer Ökonomie in der jeder jedem
etwas schenkt.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
42 / 44
Geschenke geben und erhalten
Der gesellschaftliche Wohlfahrtsverlust bei n Konsumenten und λ
Gütern durch gegenseitiges Beschenken ist
L(n, λ, δ) = n(n − 1)
λ−1
δ
λ
Der Wohlfahrtsverlust durch gegenseitiges Beschenken
I
I
I
steigt quadratisch mit der Bevölkerungsgröße
steigt mit abnehmender Rate mit der Anzahl der Güter
steigt linear mit dem Kosten eines “falschen” Geschenks
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
43 / 44
Zusammenfassung
Eine Externalität besteht, wenn ein Produzent oder ein Konsument
die Produktions- bzw. Konsumaktivitäten anderer auf eine Art und
Weise beeinflusst, die sich auf dem Markt nicht direkt widerspiegelt.
Externalitäten können durch die Vergabe von Eigentumsrechten, die
Erhebung einer Pigou-Steuer und die Vergabe von handelbaren
Zertifikaten internalisiert werden.
Ineffizienzen aufgrund von Marktversagen können durch private
Verhandlungen zwischen den betroffenen Parteien behoben werden.
Prof. Dittrich (Universität Erfurt)
Externalitäten
Winter
44 / 44