Algebra und Zahlentheorie WS 13/14 Lösungsskizzen zu Zettel 14

Algebra und Zahlentheorie
Lösungsskizzen zu Zettel 14
WS 13/14
FU Berlin
Dozent:
Tutoren:
Zentralübung:
PD Dr. Tobias Finis
Frederik Garbe, Huy Le Duc
David Müßig
Bitte beachten: Diese Lösungen sind Lösungsskizzen. Es wird kein Anspruch auf absolute
Vollständigkeit erhoben!
1. Aufgabe
4 Punkte
7
11
Bestimmen Sie µ(7, 11), µ(11, 7), ( 11 ) und ( 7 ). Zeichenne Sie für diesen Fall das unterteilte
Rechteck sowie die darin enthaltenen Gitterpunkte aus dem Gitterpunktbeweis des quadratischen
Reziprozitätsgesetzes.
7
) = ( 47 ) = 1 (da 4 Quadratzahl) und nach dem QRG gilt ( 11
) = − ( 11
) = −1
Lösung. Es ist ( 11
7
7
(da 7 ≡ 11 ≡ 3 (mod 4)).
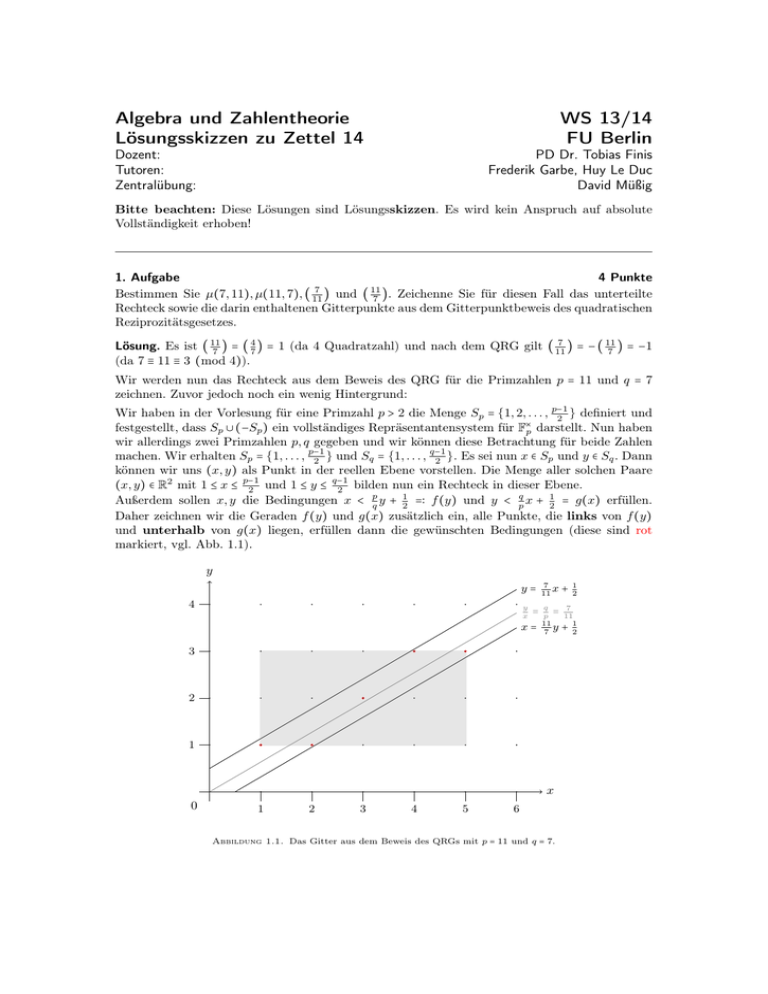
Wir werden nun das Rechteck aus dem Beweis des QRG für die Primzahlen p = 11 und q = 7
zeichnen. Zuvor jedoch noch ein wenig Hintergrund:
Wir haben in der Vorlesung für eine Primzahl p > 2 die Menge Sp = {1, 2, . . . , p−1
} definiert und
2
festgestellt, dass Sp ∪ (−Sp ) ein vollständiges Repräsentantensystem für F×p darstellt. Nun haben
wir allerdings zwei Primzahlen p, q gegeben und wir können diese Betrachtung für beide Zahlen
machen. Wir erhalten Sp = {1, . . . , p−1
} und Sq = {1, . . . , q−1
}. Es sei nun x ∈ Sp und y ∈ Sq . Dann
2
2
können wir uns (x, y) als Punkt in der reellen Ebene vorstellen. Die Menge aller solchen Paare
und 1 ≤ y ≤ q−1
bilden nun ein Rechteck in dieser Ebene.
(x, y) ∈ R2 mit 1 ≤ x ≤ p−1
2
2
Außerdem sollen x, y die Bedingungen x < pq y + 12 =∶ f (y) und y < pq x + 12 = g(x) erfüllen.
Daher zeichnen wir die Geraden f (y) und g(x) zusätzlich ein, alle Punkte, die links von f (y)
und unterhalb von g(x) liegen, erfüllen dann die gewünschten Bedingungen (diese sind rot
markiert, vgl. Abb. 1.1).
y
y=
4
7
x
11
y
x
1
2
7
= pq = 11
11
x = 7 y + 21
3
2
1
x
0
+
1
2
3
4
5
6
Abbildung 1.1. Das Gitter aus dem Beweis des QRGs mit p = 11 und q = 7.
WiSe 13/14 – FU Berlin
Algebra & Zahlentheorie – Lösungsskizzen
Aus dem Bild können wir auch µ(7, 11) und µ(11, 7) ablesen:
y + 21 und der Geraden
µ(11, 7) = 2, da es der Anzahl roter Punkte zwischen der Geraden x = 11
7
y
q
7
= p = 11 entspricht. Analog ist µ(7, 11) = 3, die Anzahl roter Punkte zwischen den Geraden
x
y
q
7
=
und y = 11
x + 21 . Zur Kontrolle:
x
p
(
11
) = 1 = (−1)2 = (−1)µ(11,7)
7
(
7
) = −1 = (−1)3 = (−1)µ(7,11)
11
✓
◇
2. Aufgabe
4 Punkte
Bestimmen Sie µ(3, p) für Primzahlen p > 3, d.h. geben Sie eine geschlossenen Formel für µ(3, p)
an.
(Hinweis: Unterscheiden Sie die Fälle p ≡ 1 (mod 6) und p ≡ −1 (mod 6).)
Lösung. Wir betrachten die Formel aus der Vorlesung:
(2.1)
∑ ∣Z ∩ [
0<y< 24
p(y − 1/2) py
, ]∣
3
3
Wir müssen also nur den Fall y = 1 betrachten. Nun gilt
1/2p
p
p+1
p
p p
<x< ⇔
≤x<
x∈Z∩[ , ]⇔
6 3
3
3
6
3
Die Länge des Intervalls [ p+1
, p3 ] ist nun
6
p
3
−
p+1
6
=
p−1
,
6
⎧
p−1
⎪
p p
⎪ 6 ,
#∣Z ∩ [ , ]∣ = µ(3, p) = ⎨ p+1
⎪
6 3
,
⎪
⎩ 6
demnach ist
p ≡ 1 (mod 6)
p ≡ −1 (mod 6)
◇
3. Aufgabe
Es sei p eine Primzahl.
(i) Wie viele normierte quadratische Polynome gibt es in Fp [x]?
(ii) Wie viele der Polynome aus (i) haben eine doppelte Nullstelle?
(iii) Wie viele der Polynome aus (i) haben zwei verschiedene Nullstellen?
(iv) Wie viele der Polynome aus (i) sind irreduzibel?
4 Punkte
Lösung. Zu (i): Ein normiertes quadratisches Polynom in Fp [x] hat die Form
f (x) ∶= x2 + ax + b
mit a, b ∈ Fp . Damit gibt es insgesamt p2 viele Möglichkeiten, solch ein Polynom zu konstruieren.
Zu (ii): Betrachte die p−q-Formel (aus der Schule bekannt): Für normierte quadratische Polynome
haben Gleichungen der Form 0 = x2 + px + q die Lösungen
√
p
p 2
x1,2 = − ± ( ) − q.
2
2
√
2
f (x) hat also genau dann eine doppelte Nullstelle, wenn ( a2 ) − b = 0, also a2 = 4b gilt. Demnach
müssen wir a, b so wählen, dass b QR modulo p ist und dann a so wählen, dass a2 = 4b gilt. Wie
wir wissen, gilt für die Anzahl quadratischer Reste modulo p
p−1
#{x ∈ Fp ∣ x ist QR modulo p} =
,
2
2
WiSe 13/14 – FU Berlin
Algebra & Zahlentheorie – Lösungsskizzen
dementsprechend haben wir p−1
viele Möglichkeiten für b und dann jeweils 2 Möglichkeiten für a
2
√
p−1
(quasi ±2 b). Also haben 2 2 = p − 1 viele Polynome aus (i) doppelte Nullstellen. Hinzu kommt
noch eine Möglichkeit, nämlich a = b = 0. Insgesamt sind es also p viele Möglichkeiten.
Zu (iii): Wenn ein Polynom zwei verschiedene Nullstellen hat, lässt es sich in der Form (x−a)(x−b)
mit a ≠ b ∈ Fp schreiben. Hier haben wir also p(p−1)
viele Möglichkeiten (wir teilen durch zwei,
2
da wir sonst jede Kombination doppelt zählen würden).
Zu (iv): f (x) ist genau dann irreduzibel in Fp [x], wenn es keine Nullstelle in Fp hat. Von solchen
Polynomen gibt es genau
p2 − p −
p(p − 1) 2p2 − 2p − p2 + p p2 − p p(p − 1)
=
=
=
2
2
2
2
viele Möglichkeiten.
◇
4. Aufgabe
4 Punkte
(i) Zeigen Sie: Wenn n = p1 ⋅. . .⋅pr ein Produkt verschiedener Primzahlen pi ist und (pi −1) ∣ (n−1)
für i = 1, . . . , r gilt, so ist an−1 ≡ 1 (mod n) für alle zu n teilerfremden Zahlen a.
(ii) Zeigen Sie, dass n1 = 561 und n2 = 1105 die soeben aufgestellte Bedingung erfüllen.
Lösung. Zu (i): Wir wissen, dass ap−1 ≡ 1 (mod p) für alle Primzahlen p und zu p teilerfremde
Zahlen a gilt. Wegen (pi − 1) ∣ (n − 1) für alle i gilt daher auch
an−1 ≡ 1 (mod pi ) für 1 ≤ i ≤ r
bzw. an−1 − 1 ≡ 0 (mod pi ). Da ggT(pi , pj ) = 1 für i ≠ j, gilt auch
an−1 − 1 ≡ 0 (mod n) ⇔ an−1 ≡ 1 (mod n).
Zu (ii): Es ist n1 = 561 = 3 ⋅ 11 ⋅ 17. Außerdem gilt
p1 − 1 = 2 ∣ 560 = n1 − 1,
p2 − 1 = 10 ∣ 560 = n1 − 1,
p3 − 1 = 16 ∣ 560 = n1 − 1 (da 560 = 35 ⋅ 16).
Und für n2 = 1105 = 5 ⋅ 13 ⋅ 17 gilt
p1 − 1 = 2 ∣ 1104 = n2 − 1,
p2 − 1 = 12 ∣ 1104 = n2 − 1 (da 1104 = 12 ⋅ 92),
p3 − 1 = 16 ∣ 1104 = n2 − 1 (da 1104 = 16 ⋅ 69).
◇
3