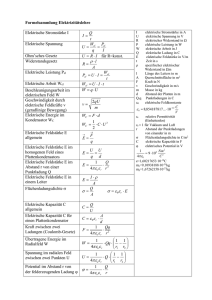
Physik Formeln und Gesetze: Kinematik, Dynamik, Elektrizität
Werbung
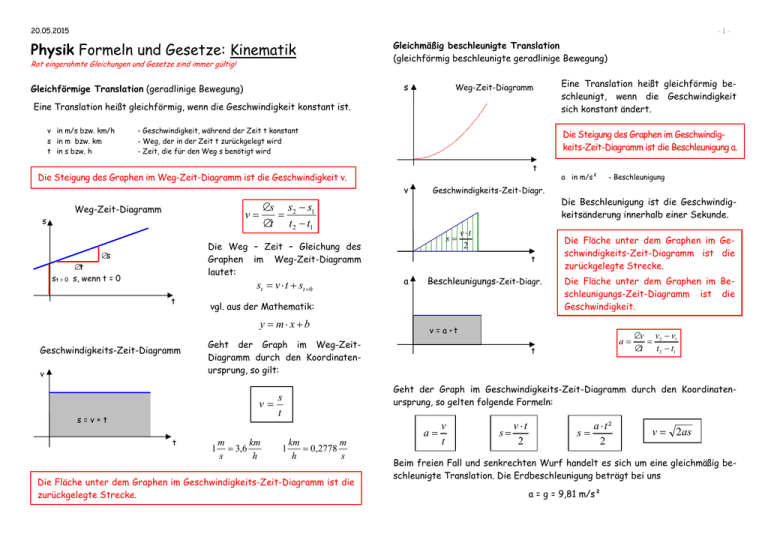
20.05.2015 -1- Physik Formeln und Gesetze: Kinematik Rot eingerahmte Gleichungen und Gesetze sind immer gültig! Gleichmäßig beschleunigte Translation (gleichförmig beschleunigte geradlinige Bewegung) s Gleichförmige Translation (geradlinige Bewegung) Weg-Zeit-Diagramm Eine Translation heißt gleichförmig, wenn die Geschwindigkeit konstant ist. v in m/s bzw. km/h s in m bzw. km t in s bzw. h - Geschwindigkeit, während der Zeit t konstant - Weg, der in der Zeit t zurückgelegt wird - Zeit, die für den Weg s benötigt wird Die Steigung des Graphen im Geschwindigkeits-Zeit-Diagramm ist die Beschleunigung a. t Die Steigung des Graphen im Weg-Zeit-Diagramm ist die Geschwindigkeit v. a in m/s² v Weg-Zeit-Diagramm s st = 0 Die Weg – Zeit – Gleichung des Graphen im Weg-Zeit-Diagramm lautet: ∆s ∆t s, wenn t = 0 st = v ⋅ t + st =0 t Geschwindigkeits-Zeit-Diagramm v t s= v ⋅t 2 t a Beschleunigungs-Zeit-Diagr. m km 1 = 3,6 s h km m 1 = 0,2778 h s Die Fläche unter dem Graphen im Geschwindigkeits-Zeit-Diagramm ist die zurückgelegte Strecke. Die Fläche unter dem Graphen im Geschwindigkeits-Zeit-Diagramm ist die zurückgelegte Strecke. Die Fläche unter dem Graphen im Beschleunigungs-Zeit-Diagramm ist die Geschwindigkeit. v = a *t Geht der Graph im Weg-ZeitDiagramm durch den Koordinatenursprung, so gilt: s v= t s=v∗t Die Beschleunigung ist die Geschwindigkeitsänderung innerhalb einer Sekunde. vgl. aus der Mathematik: y = m⋅ x +b - Beschleunigung Geschwindigkeits-Zeit-Diagr. ∆s s2 − s1 = ∆t t 2 − t1 v= Eine Translation heißt gleichförmig beschleunigt, wenn die Geschwindigkeit sich konstant ändert. a= t ∆v v2 − v1 = ∆t t 2 − t1 Geht der Graph im Geschwindigkeits-Zeit-Diagramm durch den Koordinatenursprung, so gelten folgende Formeln: a= v t s= v ⋅t 2 s= a ⋅t² 2 v = 2as Beim freien Fall und senkrechten Wurf handelt es sich um eine gleichmäßig beschleunigte Translation. Die Erdbeschleunigung beträgt bei uns a = g = 9,81 m/s² 20.05.2015 -2- Gleichförmige Rotation (Rotationsgeschwindigkeit ist konstant) Winkelgeschwindigkeit oder auch Kreisfrequenz: ω= α t = Die Zentralbeschleunigung ist proportional zur Winkelund der Umfangsgeschwindigkeit: Unter Energie E versteht man die Fähigkeit eines Körpers, Arbeit W zu verrichten. Energie = Arbeitsvermögen oder Arbeitsvorrat. 360° 2 ⋅ π = = 2 ⋅π ⋅ f T T α in Bogenmaß, (Grad) - Winkel T in s - Zeit für einen Umlauf, Periode f in Hz, 1/s - Umläufe pro Sekunde, Frequenz n in 1/min - Drehzahl, Umläufe pro Minute Umfangsgeschwindigkeit: Arbeit, Energie Leistung: W =F ⋅s = m⋅a⋅s Hubarbeit: t in s - Zeit ω in 1/s - Winkelgeschwindigkeit (Kreisfrequenz) r in m - Radius 2 ⋅π ⋅ r v = ω ⋅r = = 2 ⋅π ⋅ r ⋅ f T Beschleunigungsarbeit: Elektrische Arbeit: Energieeinheiten: a = Erdbeschleunigung s = Höhe U in V - 1 W = mv 2 2 W =U ⋅ I ⋅ t = P ⋅ t 1Nm = 1 Spannung I in A - Strom t in s - Zeit P in W - Leistung kgm 2 = 1J = 1VAs = 1Ws s2 1eV = 1,602 ⋅10 −19 J Unter Leistung P versteht man das Verhältnis der verrichteten Arbeit zur benö- v2 a = ω ⋅v = ω ⋅r = r 2 f = 1 T Physik Formeln und Gesetze: Dynamik Arbeit Leistung = Zeit W P= t Die Leistung P wird in W = VA =J/s gemessen tigten Arbeitszeit. Ursache jeder Änderung des Bewegungszustandes ist das Wirken von Kräften. Hebelgesetz: Unter einem Hebel versteht man einen starren, um eine Achse drehbaren Körper. Kraft F und Hebelarm l steF ⋅ l1 = F2 ⋅ l 2 hen senkrecht aufeinander. Das Verhältnis der wirkenden Kraft zur erzielten Beschleunigung ist für jeden Körper eine konstante Größe. Es ist die Masse. Als Dichte bezeichnet man das Verhältnis der Masse eines Körpers zu seinem Volumen. Newtonsche Axiome: Dichte = Beschleunigung = Kraft Masse a= F m a in m/s² - Beschleunigung F in N = kgm/s² - Kraft m in kg - Masse Körpermasse Volumen ρ= m V ρ in kg/dm³ = g/cm³ - Dichte Wirkt auf eine Fläche A eine Kraft F, so entsteht der Druck p Masse ist die Eigenschaft jeder Materie, träge und schwer zu sein. Bei einer Kreisbewegung wirkt die Zentripetalkraft FZ der entstehenden Fliehkraft (Zentrifugalkraft) FF entgegen. Beide Kräfte sind gleich groß. Druck = Kraft Fläche Schweredruck p= F A p=h ⋅ ρ ⋅ g P in N/m² = Pa – Druck F in N – Kraft A in m² - Fläche h in m - Höhe 20.05.2015 -3- Physik Formeln und Gesetze: Kalorik Es gibt verschiedene Temperaturskalen. Die Kelvin-Skala hat ihren Nullpunkt bei der tiefstmöglichen Temperatur, dem absoluten Nullpunkt. Die CelsiusSkala hat ihren Nullpunkt beim Erstarrungspunkt von Wasser und beim Siedepunkt sind 100°C erreicht. 0 K = -273°C 273K = 0°C Qm = Q1 + Q2 Längenausdehnung 373K = 100°C Die Temperaturdifferenz wird in Kelvin gemessen. ∆ϑ = ϑ2 − ϑ1 Die Wärmeinhalte der an der Mischung beteiligten Stoffe Q1 und Q1 addieren sich zum Gesamtwärmeinhalt Qm: θ1 in K od. °C - Anfangstemperatur θ2 in K od. °C - Endtemperatur ∆θ in K - Temperaturdifferenz T - Formelzeichen für Temperaturangaben in Kelvin ∆l = l1 ⋅ α ⋅ ∆ϑ ∆ϑ = ϑ 2 − ϑ1 l 2 = l1 (1 + α ⋅ ∆ϑ ) ∆l = l 2 − l1 γ = Die zur Erwärmung eines Körpers oder einer Flüssigkeit notwendige Q = c ⋅ m ⋅ ∆ϑ Q in kJ - Wärmemenge c in kJ/(kgK) - spezifische Wärmekapazität m in kg - Masse Bei Abkühlung wird diese Energie abgegeben. in m - Ausgangslänge in m - Endlänge in m - Längenänderung in 1/K - Längenausdehnungskoeffizient Volumenausdehnung von Gasen (p = const.) Vϑ = V0°C ⋅ (1 + γ ⋅ ϑ ) Wärmemenge l1 l2 ∆l α V0°C in m³ - Volumen bei 0°C Vθ in m³ - Volumen bei θ in °C θ in °C - Temperatur 1 273K Zustandsgleichung der Gase p in Pa - Druck V in m³ - Volumen T in K - absolute Temperatur p1 ⋅ V1 p 2 ⋅ V2 = T1 T2 Zum Schmelzen eines Stoffes wird die Schmelzwärme benötigt: QS = q S ⋅ m QS in kJ - Wärmemenge qS in kJ/kg - spezifische Schmelzwärme m in kg - Masse Bei Erstarren wird diese Energie abgegeben. Sonderfälle der Zustandsgleichung Bezeichnung: isobare isochore isotherme Zustandsänderung Die Verdampfungswärme eines Stoffes beträgt: QD = q D ⋅ m QD in kJ - Wärmemenge qD in kJ/kg - spezifische Verdampfungswärme m in kg - Masse Beim Kondensieren wird diese Energie abgegeben. Bedingung p = const. V = const. T = const. Formel V1 T1 = V2 T2 p1 T1 = p 2 T2 p1 V2 = p 2 V1 Gesetz Für Wasser gilt: kJ c = 4,19 kg ⋅ K kJ qS = 333 kg kJ qD = 2260 kg Gay-Lussac Boyle-Mariotte 20.05.2015 -4- Physik Formeln und Gesetze: Elektrik Die kleinste elektrische Ladungsmenge Q ist die Elementarladung des Elektrons (negativ) bzw. des Protons (positiv). e = 1,602 ⋅ 10 -19 As Die Elementarladung betrögt Strom ist die Ladungsmenge Q, die sich pro Sekunde durch einen Querschnitt bewegt. Strom = Ladung Zeit I= Q t I in A - Strom Q in As - Ladung t s - Zeit in Werden elektrische Ladungen getrennt, entsteht zwischen den Ladungen ein elektrisches Feld. Die elektrische Feldstärke E hängt von der angelegten Spannung U und dem Abstand s der Platten des Kondensators ab. E= E U s U s in V/m - elektrische Feldstärke in V - elektrische Spannung in m - Plattenabstand Befindet sich in einem elektrischen Feld E eine Ladung Q, so wirkt auf sie die Kraft F. E in V/m - elektrische Feldstärke Q in As - elektrische Ladung F in N - Kraft F = E ⋅Q Die Spannung ist das Bestreben getrennter Ladungen sich auszugleichen. Um elektrische Ladungen zu trennen, muss die Arbeit W verrichtet werden, die von der Ladungsmenge Q und der elektrischen Feldstärke E abhängt. Ohmsches Gesetz: In einem Leiter ist die Stromstärke I der Spannung U direkt und dem Widerstand R umgekehrt proportional. Widerstand = Spannung Strom R= U in U I V - Spannung R in Ω - Widerstand I in A - Strom Widerstandsberechnung: Wie stark der Stromfluss in seiner Stärke behindert wird, liegt an der Länge und dem Querschnitt des Leiters und seinem Material. l in m - Länge l l⋅ρ R= = κ⋅A A R in Ω - Widerstand A in mm² - Leiterquerschnitt W = F ⋅ s = E ⋅ Q⋅ s = U ⋅Q⋅ s s W = Q ⋅U E in V/m - elektrische Feldstärke U in V s in m - Plattenabstand F in N - Kraft W in Nm - elektrische Spannung - Arbeit, Energie Durchläuft ein Elektron mit der Elementarladung e- = 1,602·10-19As die Spannung U von 1V, dann hat das Elektron die Energie von 1 eV = 1V · 1,602·10-19As = 1,602·10-19 Nm 1 Nm = 6,24·1018 eV ρ in (Ωmm²)/m – spez. Widerstand Elektrische Leistung: Elektr. Arbeit/Energie: P= W =U ⋅I t W =U ⋅ I ⋅t κ in m/(Ωmm²) – elektrische Leitfähigkeit ( früher: γ ) Die Masse eines Elektrons beträgt: P in W=VA=J/s - elektr. Leistung Die Masse eines Protons ist ungefähr genauso groß, wie die des Neutrons und beträgt: t in s - Zeit W in J = Nm = Ws - Arbeit, Energie U in V - Spannung I in A - Strom me = 9,11·10-31kg mp = mn = 1,67·10-27kg 20.05.2015 -5- Optik: Linsen- und Parabolspiegel-Gleichungen B b = G g 1 1 1 = + f g b B G b g f in m in m in m in m in m - Bildgröße - Gegenstandsgröße - Bildweite - Gegenstandweite - Brennweite 2 · f = r - Radius c in m/s – Ausbreitungsgeschwindigkeit λ in m - Wellenlänge f in Hz - Frequenz c=λ⋅ f Wellen: Lichtgeschwindigkeit im Vakuum (genähert): c0 = 300000000 m/s = 3· 108m/s Schallgeschwindigkeit: c = 350 m/s Photonenenergie: WPh in J oder eV WPh = h ⋅ f = h ⋅ c λ = m ⋅ c² Photoeffekt: h ⋅ f = W A + Wkin - Photonenenergie h = 6,626 · 10-34Js - Plancksches Wirkungsquantum c = 3 · 108 m/s WA in J oder eV - Lichtgeschwindigkeit - Ablösearbeit Umrechnung: Länge: 10-3km Bemerkung: 10³ = 1· 10³ Si-Vorsätze: Physik Formeln und Gesetze: Licht (Schall) Yotta Zetta Exa Peta Tera Giga Mega Kilo Hekto Deka Y Z E P T G M k h da Dezi Zenti Milli Mikro Nano Piko Fempto Atto Zepto Yocto d c m µ n p f a z y 10-6km² 1 000 000 000 1 000 000 1 000 100 10 1 0,1 0,01 0,001 0,000 001 0,000 000 001 Konstanten: Lichtgeschwindigkeit: Schallgeschwindigkeit: Elektronenmasse: Elementarladung: Protonen- u. Neutronenmasse: c0 = 300000000 m/s = 3· 108m/s c = 350 m/s me = 9,11·10-31kg e = 1,602·10-19As mp = mn = 1,67·10-27kg Für Wasser gilt: = 1m = 10dm = 100cm = 1000mm = 106µm = 1m² = 102dm² = 104cm² = 106mm² Volumen: 1m³ = 103dm³ = 106cm³ = 109mm³ Energieeinheiten: kgm 1Nm = 1 2 s 2 = 1J = 1VAs = 1Ws 1 eV = 1,602 ⋅ 10 −19 J kJ Spez. Wärmekapazität: c = 4,19 Spez. Schmelzwärme: q S = 333 1Å (Ångström)= 10-10m Fläche: 1024 1021 1018 1015 1012 109 106 103 102 101 100 10-1 10-2 10-3 10-6 10-9 10-12 10-15 10-18 10-21 10-24 spez. Verdampfungswärme kg ⋅ K kJ kg q D = 2260 kJ kg = 4,19 J g⋅K