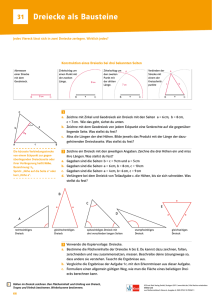
Power Point zum Plan der Durchführung
Werbung

PLAN DER DURCHFÜHRUNG Abstraktion Hinführung ( Motivation, Sachbegegnung) Schülervermutungen Kopfrechnen Kopfgeometrie Rechenfertigkeitsübung Zielangabe Anwendung / Übung Erarbeitung ARTIKULATION Kopfrechnen Kopfgeometrie Rechenfertigkeitsübung Hinführung • • Motivation Sachbegegnung Zielangabe Schülervermutungen Erarbeitung Abstraktion Anwendung Übung / Erarbeitung Welche Arbeitsaufträge erhalten die Schüler? Beispielaufgaben!! Bezug auf Ziele? Welches Material/Welche Hilfen erhalten die Schüler? AB mit konkreten Aufgaben etc. Welche Impulse gibt der Lehrer, welche Schülerantworten werden erwartet? Wie wird differenziert? Beispiele! In welcher Sozialform wird gearbeitet? (Warum?) Abstraktion - Wie werden die Ergebnisse der Schüler aus der Erarbeitungsphase präsentiert? Warum? - Welche Impulse/Hilfen sind nötig, damit die Schüler die Formel/Lösung herleiten können? Konkrete Formulierung! - Wie kann für eine ausreichende Verbalisierung gesorgt werden? Tafelbild - Zielangabe - Datum (Problemfrage) -Schüler- Stundenthema vermutungen - erklärende Grafik, - Formel -Merksatz, -Antwort auf die Problemfrage genetisches Tafelbild -> entsteht im Verlauf der Stunde statisches Tafelbild -> wurde vor der Stunde vorbereitet KONKRETES BEISPIEL -Berechne den Flächeninhalt vom Dreieck Möglichkeiten der Herleitung Voraussetzungen Zielangaben Grobziel • Die Schüler sollen ein Dreieck zu einem flächengleichen Rechteck umwandeln können. • Die Schüler sollen Aufgaben zum Flächeninhalt im Dreieck lösen können. • Die Schüler lösen mit Hilfe der Rechtecksformel Aufgaben zum Flächeninhalt des Dreiecks. • Die Schüler sollen den Flächeninhalt vom Dreieck bestimmen können. • Die Schüler lernen die Formel zur Berechnung des Flächeninhalts kennen. Feinziele Die Schüler sollen… • erkenne, dass ein Dreieck den gleichen Flächeninhalt wie ein Rechteck hat. • die Flächeninhaltsformel des Dreiecks herleiten können. • die Herleitung der Flächeninhaltsformel für das Dreieck verstehen. • ein Dreieck in ein flächengleiches Rechteck umbauen können. • in Gruppenarbeit das Problem lösen. • Beziehungen zwischen den Seiten im Dreieck und im Rechteck erkennen und benennen können. Vergleich von Erarbeitungsphasen!