Das Quadrat - Mathe Online
Werbung

Slide 1
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
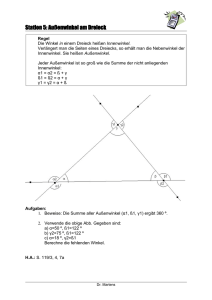
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
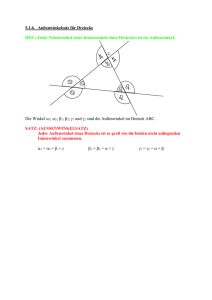
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 2
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 3
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 4
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 5
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 6
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 7
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 8
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 9
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 2
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 3
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 4
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 5
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 6
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 7
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 8
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2
Slide 9
Das allgemeine Dreieck
Das
allgemeine
Dreieck
C
Bezeichnung
a
b
A
c
B
In jedem Dreieck ist die Summe der
drei Innenwinkel 180°.
Winkelsumme
+ + = 180°
Jeder Innenwinkel hat zwei gleich große
Außenwinkel.
Außenwinkel
Jeder Innenwinkel und sein zugehöriger
Außenwinkel sind supplementär.
Supplementäre Winkel
+ 1 = 180° + 1 = 180°
+ 1 = 180°
Die Summe der Außenwinkel ist 360°.
Summe der Außenwinkel
1 + 1 + 1 = 360°
Jeder Außenwinkel ist genauso groß wie die
Summe der beiden nicht anliegenden Innenwinkel.
Außenwinkelsatz
Der Flächeninhalt
C
hc
hc
2
A
c
B
hc
A=c· 2
Der Flächeninhalt
Der Flächeninhalt
C
ha
C
C
hb
2
2
hc
A
2
c
A=c·
b
a
B
hc
2
A
B
A=a·
ha
2
B
A
A=b
·
hb
2