Station 5: Außenwinkel am Dreieck
Werbung
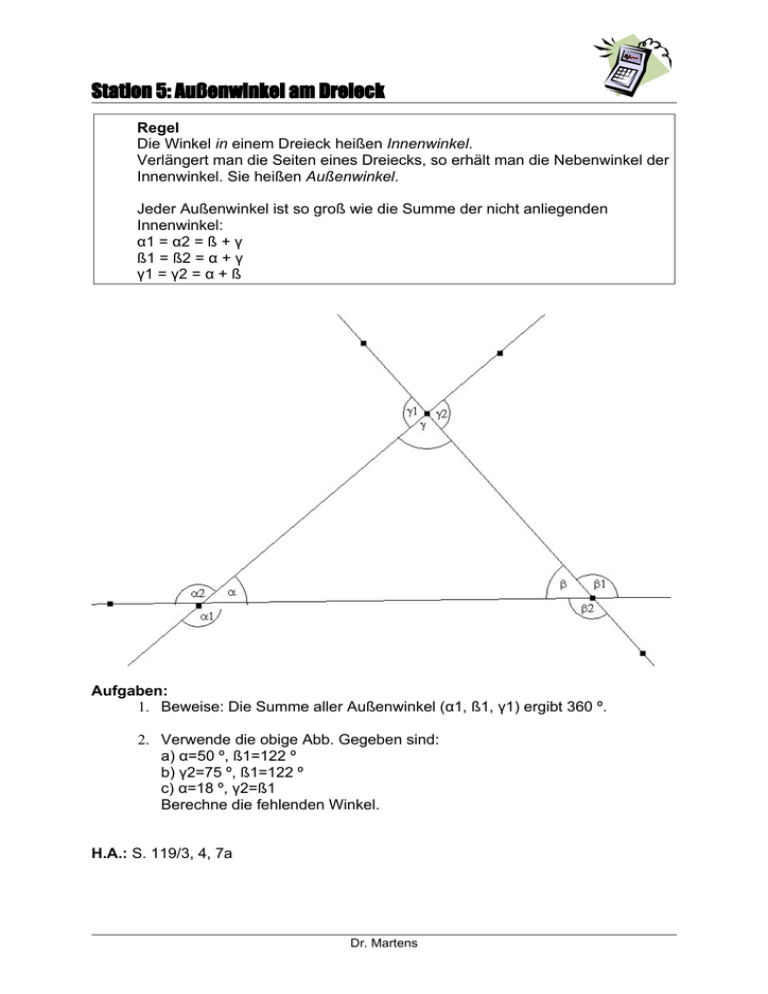
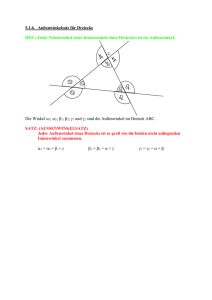
Station 5: Außenwinkel am Dreieck Regel Die Winkel in einem Dreieck heißen Innenwinkel. Verlängert man die Seiten eines Dreiecks, so erhält man die Nebenwinkel der Innenwinkel. Sie heißen Außenwinkel. Jeder Außenwinkel ist so groß wie die Summe der nicht anliegenden Innenwinkel: α1 = α2 = ß + γ ß1 = ß2 = α + γ γ1 = γ2 = α + ß Aufgaben: 1. Beweise: Die Summe aller Außenwinkel (α1, ß1, γ1) ergibt 360 º. 2. Verwende die obige Abb. Gegeben sind: a) α=50 º, ß1=122 º b) γ2=75 º, ß1=122 º c) α=18 º, γ2=ß1 Berechne die fehlenden Winkel. H.A.: S. 119/3, 4, 7a Dr. Martens