Additions- und Multiplikationssatz

Mathematik J 1 / 2
Additions-/Multiplikationssatz
In einer Leichtathletikmannschaft sind 60% Läufer. 30 % der Mannschaft Additionssatz:
nehmen an Kurz- und 40% an Langstreckenwettbewerben teil. Kann
man aus diesen Informationen diejenigen bestimmen, die auf beiden
kennt man von zwei Ereignissen A und B die
Streckenarten starten? (Mengendiagramm!) [Antwort: 10%, da sich die
Wahrscheinlichkeiten P(A), P(B), so lässt sich für
Läufer alle aus den 60% der Mannschaft rekrutieren]
Für zwei Ereignisse A und B mit A  B=Ø gilt: P(A  B)=P(A) + P(B)
sog. Spezieller Additionssatz
Sind A und B beliebig, also insbesondere ABØ, so kann man
AB durch drei Teilmengen
(disjunkte!) zusammensetzen
(Mengenbild). Es gilt:
das Ereignis A  B ( "Addition") die
Wahrscheinlichkeit berechnen. Allerdings braucht
man dazu noch P(A  B), was im konkreten Fall
recht günstig zu berechnen ist.
Beispiel:
Experiment: Doppelwurf einer Münze.
Ereignis E: Wappen im ersten oder zweiten Wurf.
Man berechne P(E).
A  B=A \ B  (A  B)  B \ A. Darauf lässt sich der spezielle
Additionssatz anwenden:
P(A  B)=P(A \ B) + P(A  B) + P(B \ A), ersetzt man die
Differenzmenge, dann gilt:
P(A  B)=P(A) - P(A  B) + P(A  B) + P(B) - P(A  B)
und dann: P(AB)= P(A)+P(B)- P(AB)
Lösung:
A: Wappen im 1. Wurf, B: Wappen im zweiten
Wurf. E=A  B
P(E)= P(A) + P(B) - P(A  B)
= 0,5+0,5-0,5² = 0,75.
Additionssatz für bel. Ereignisse A, B
Wegen P(A  B)=0 ↔ A  B=Ø, ist der spezielle Additionssatz ein
Sonderfall des allg. Additionssatzes.
(a) Sei A: „w im 2. Zug“
(b) Sei B: „w im 2. Zug, falls w bereits im 1.
Zug.“
Übungsaufgabe:
Eine Urne enthalte 2 weiße (w) und 2 schwarze (s) Kugeln. Es wird
zweimal eine Kugel gezogen und es wird ihre Farbe notiert.
(a) Man bestimme mittels eines Baudiagramms die
Wahrscheinlichkeit für „w im 2. Zug“, wenn mit (ohne)
Zurücklegen gezogen wird.
(b) Wie groß ist die Wahrscheinlichkeit für „w im 2. Zug wenn
schon im 1. Zug w gezogen wurde?
Mit Zurücklegen:
(a)
P(A) =  12  12  12  12 
1
2
(b)
1
P(B) = /2
Die Wahrscheinlichkeit, dass ein Ergebnis e eintritt unter der Bedingung,
dass ein Ereignis A bereits eingetreten ist, berechnet sich demnach als:
 0; falls e  A

PA (e)   P(e)
 P( A) ; falls e  A

Ohne Zurücklegen:
(a)
P(A)= 2  3
1
(b)
1
P(B)= /3
Betrachtet man statt des Ergebnisses e ein beliebiges Ereignis B, dann
ist die Wahrscheinlichkeit, dass B eintritt, wenn A bereits eingetreten ist:
PA(B) = P(A  B) , da nur die Ergebnisse zählen, die in AB liegen.
P(A)
- 1/3 -
1
 12  32 
1
2
Mathematik J 1 / 2
Additions-/Multiplikationssatz
Sind A, B beliebige Ereignisse mit P(A)0, dann ist PA(B) die
durch A bedingte Wahrscheinlichkeit von B. Es gilt:
Bedingte Wahrscheinlichkeit
... voneinander abhängige Ereignisse
(insbesondere im Urnenmodell "ohne
Zurücklegen")
P(A  B)
PA(B) =
P(A)
Mit P(A) und P(AB) haben wir PA(B) berechnet. In
vielen Fällen sind P(A) und PA(B) bekannt, sodass
umgekehrt P(AB) berechnet werden kann:
Der allgemeine Multiplikationssatz:
Ist P(A)  0, dann gilt: P(AB) = P(A)  PA(B)
Beisp.:
Der Multiplikationssatz
... die Wahrscheinlichkeiten der
beteiligten Ereignisse A und B werden
bei der Berechnung von P(AB)
"miteinander multipliziert".
Beachte dabei:
Baumdiagramm zum
zweimaligen Ziehen
ohne Zurücklegen aus
einer Urne mit 4 roten
und 5 schwarzen
Kugeln:
allgemeiner Fall:
A und B sind evt. voneinander abhängig.
A: „im 1. Zug rote Kugel“
B: „im zweiten Zug rote
Kugel“
Die gezeichneten Pfade
entsprechen den
Ereignissen:
A B, A B, A B, A B
Am Pfadende stehen die
Wahrscheinlichkeiten,
wie sie sich aus dem
Multipli-kationssatz
ergeben. (vgl.:
„Pfadregel“).
Spezialfall: A und B sind unabhängig
.... siehe Definition .
- 2/3 -
Mathematik J 1 / 2
Additions-/Multiplikationssatz
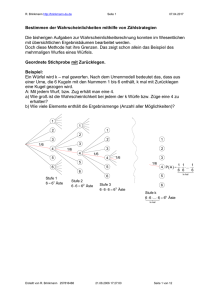
Eine Urne enthalte 2 weiße und 1 rote Kugel. Diese 3 Kugeln tragen die Nummern 1 bis 3.
1
2
Einmaliges Kugelziehen ergibt P({rot}) = /3 und P({weiß}) = /3 .
Zieht man zweimal eine Kugel, einmal mit und einmal ohne Zurücklegen, so ergeben sich mit dem untenstehenden
Baumdiagramm die entsprechenden Ergebnismengen.
Für die Paare nummerierter Kugeln (die beim zweimaligen Ziehen gezogen werden) kann man Gleichverteilung
annehmen.
Fasst man nun nach Farben zusammen, dann ist die Wahrscheinlichkeit für „weiß im ersten und rot im zweiten Zug“
2
1
beim Ziehen mit Zurücklegen /9
beim Ziehen ohne Zurücklegen /3
Der Unterschied entsteht dadurch, dass sich es sich beim Ziehen mit Zurücklegen um voneinander unabhängige
Züge und beim Ziehen ohne Zurücklegen um voneinander abhängige Züge handelt.
Auf Ereignisse übertragen bedeutet dies: P({die gezogene Kugel ist rot}) ist bei unabhängigen Durchführungen des
Experiments auf jeder Stufe gleich, wogegen dies bei abhängiger Durchführung nicht zu gelten braucht.
Sei nun A: weiß im 1. Zug
und B:
rot im 2. Zug , so gilt nur beim Ziehen mit Zurücklegen, also bei unabhängiger
Durchführung, die Beziehung:
P(A  B) = P(A) - P(B)
Daraus ergibt sich also folgende
Definition: Zwei Ereignisse A und B heißen unabhängig, wenn gilt:
P(A  B) = P(A) - P(B),
andernfalls sind A und B abhängig.
- 3/3 -