Folien_423_TECHNIK
Werbung

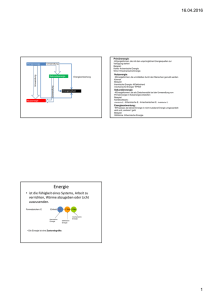
2.3 ULTRASCHALL-TECHNIK Inhalt dieses Vorlesungsteils - ROADMAP 42 Von der Kavitation zur Sonochemie 21 Industrieller Einsatz von Ultraschall 22 Physikalische Grundlagen I – Was ist Ultraschall 23 Einführung in die Technik des Leistungsultraschalls (LUS) 24 Physikalische Grundlagen II – Was ist Kavitation? 25 Applikationen des LUS FOLIE 1 GMBU 2.3 ULTRASCHALL-TECHNIK Gesamtprozess (A) Stabschwinger (B)Flächenschwinger Transducer Piezoelement beschalltes Volumen Stufenhorn Piezoelement Transducer beschalltes Volumen Kühlmantel Hohe akustische Amplitude (longitudinal, 80-100 µm) der Sonotroden und Boosterhörner Geringe akustische Amplitude (transversal, 20 µm) Hohe akustische Intensität Fokussierung der Schallenergie auf den Intensität auf das gesamte Flüssigkeits- Kegel unterhalb der Sonotrode volumen Vergleichmäßigung der akustischen Temperaturkontrolle notwendig FOLIE 2 GMBU 2.3 ULTRASCHALL-TECHNIK Gesamtprozess Energiefluss im Ultraschallprozess Elektrische Energie Akustische Energie Kavitation Wärme Radikalbildung fluidmech. Bewegung Reaktionsprodukte FOLIE 3 GMBU 2.3 ULTRASCHALL-TECHNIK Piezoelektrisch Transducerprinzipien Nutzung des Piezoeffekts über den gesamten US-Frequenzbereich Anwendung für sensorische Messaufgaben, medizinische Bildgebung und LUS-Anwendungen Magnetorestriktiv Änderung der Abmessungen der aktiven Schicht unter Einfluss eines magnetischen Feldes Elektromagnetisch Anwendung bei niedrigen Frequenzen, insbesondere LUS Nutzung elektromagnetischer Felder zur Erzeugung von Vibrationen (z.B. Schwingspule im Permanentmagnetfeld) Pneumatisch Anwendung als Lautsprecher und Mikrofon im Hörschallbereich Sprühdüsen (Pfeifen) zur Erzeugung von Aerosolen in Gasen im Hörschall und unteren US-Bereich Nutzung in Beschichtungsprozessen, Reinigungsprozessen und zur Feuchtigkeitskontrolle Hydraulisch Einsatz von Hochdruckstrahldüsen (Venturi) zur Erzeugung von Emulsionen oder Kavitationsblasen FOLIE 4 GMBU 2.3 ULTRASCHALL-TECHNIK Anwendung FOLIE 5 GMBU 2.3 ULTRASCHALL-TECHNIK Prinzip Piezoelektrizität Durch die gerichtete Verformung eines piezoelektrischen Materials kommt es innerhalb der Elementarzellen zu einer Ladungstrennung (Verschiebung der Ladungs-Schwerpunkte) und dabei zur Ausbildung elektrischer Dipole. Die Aufsummierung über alle Elementarzellen des Kristalls führt zu einer makroskopisch messbaren elektrischen Spannung. Gerichtete Verformung bedeutet, dass der angelegte Druck nicht von allen Seiten auf die Probe wirkt, sondern beispielsweise nur von gegenüberliegenden Seiten aus. Umgekehrt kann durch Anlegen einer elektrischen Spannung der Kristall bzw. Piezokeramik verformt werden (inverser piezoelektr. Effekt). Wie auch jeder andere Festkörper können piezoelektrische Körper me- Piezoelektrischer Effekt chanische Schwingungen ausführen. Bei Piezoelektrika können diese Schwingungen einerseits elektrisch angeregt werden, bewirken andererseits aber auch wieder eine elektrische Spannung. Die Frequenz der Schwingung Der direkte Piezoeffekt wurde im ist nur von der Schallgeschwindigkeit (eine Materialkonstante) und den Ab- Jahre 1880 von den Brüdern messungen des piezoelektrischen Körpers abhängig. Dadurch sind piezo- Jacques und Pierre Curie bei elektrische Bauteile auch für Oszillatoren geeignet (z. B. Schwingquarze). Untersuchungen mit Turmalinkristallen entdeckt. FOLIE 6 GMBU 2.3 ULTRASCHALL-TECHNIK Piezoelektrische Materialien Der Piezoeffekt kann nur in nichtleitenden und dielektrischen Materialien auftreten. Weiterhin sind alle nichtleitenden ferroelektrischen Materialien bzw. Materialien mit permanentem elektrischen Dipol auch piezoelektrisch, beispielsweise Bariumtitanat und Blei-Zirkonat-Titanat (PZT). Jedoch verhält sich nur ein Teil der Piezoelektrika ferroelektrisch. Bei Kristallen ist die Kristallsymmetrie ein weiteres Kriterium für das Auftreten der Piezoelektrizität. Das bekannteste Material mit Piezoeigenschaften ist Hystereseverhalten von Ferroelektrika Quarz (SiO2). Technisch genutzte Materialien, die einen stärkeren PiezoEffekt als Quarz zeigen, leiten sich oft von der Perowskit-Struktur ab, z. B. Bariumtitanat (BaTiO3). Industriell genutzte Piezoelemente sind zumeist Keramiken. Diese Keramiken werden aus synthetischen, anorganischen, ferroelektrischen und polykristallinen Keramikwerkstoffen gefertigt. Typische Basismaterialien für Hochvolt-Aktoren sind modifizierte Blei-Zirkonat-Titanate (PZT) und für Niedervolt-Aktoren Blei-Magnesium-Niobate (PMN). FOLIE 7 GMBU 2.3 ULTRASCHALL-TECHNIK Piezokeramische Materialien Der Stoffverbund der PZT-Keramiken (Pb,O,Ti/Zr) kristallisiert in der Perowskit-Kristallstruktur. Unterhalb der piezoelektrischen Curietemperatur bildet sich durch Verzerrungen der idealen Perowskit-Struktur ein Dipolmoment aus. Bei keramischen Piezoelementen sind die internen Dipole nach dem Sinterprozess noch ungeordnet, weshalb sich keine piezoelektrischen Eigenschaften zeigen. Die Weissschen Bezirke oder Domänen besitzen eine willkürliche räumliche Orientierung und gleichen sich gegenseitig aus. Eine deutlich messbare piezoelektrische Eigenschaft lässt sich erst durch ein äußeres elektrisches Gleichfeld aufprägen (einige 106 V/m), während das Material bis knapp unter die Curie-Temperatur erwärmt und wieder abgekühlt wird. Die eingeprägte Orientierung bleibt danach zum großen Teil erhalten (remanente Polarisation) und wird als Polarisationsrichtung bezeichnet. Perowskit-Einheitszelle von Piezokeramiken. Unterhalb der Curie-Temperatur bildet sich ein Dipol aus. Einprägen einer Polarisationsrichtung durch Ausrichtung der Dipole in einem elektrischen Feld FOLIE 8 GMBU 2.3 ULTRASCHALL-TECHNIK Elektromechanische Grundgleichungen Für die Indizierung richtungsabhängiger Eigenschaften wird ein x,y,z-Koordinatensystem verwendet. Dessen Achsen bezeichnen die Ziffern 1,2,3 (Achse 3 entspricht der Polarisationsachse) . Die Scherungen an diesen Achsen werden mit 4,5,6 beziffert. Die Tensoren werden nach dieser Nomenklatur indiziert. Verknüpfung elektrischer und elastischer Materialeigenschaften Im Bereich geringer elektrischer und mechanischer Amplituden (Kleinsignalwerte) ergeben sich zwischen den elastischen Deformations (S) - bzw. Spannungs (T) -Komponenten und den Komponenten des elektrischen Feldes E bzw. der dielektrischen Verschiebung D lineare Beziehungen. Aufgrund der Richtungsabhängigkeit (Anisotropie) resultieren die dielektrische, piezoelektrische und elastische “Konstante“ als tensorielle physikalische Größen. In vereinfachter Form sind die Grundzusammenhänge der elektrischen und elastischen Eigenschaften (für eine statische bzw. quasistatische Anwendung), wie folgt darstellbar: T D = d T E E S=s T d E D elektrische Flußdichte T mechanische Spannung E elektrisches Feld S mechanische Dehnung d piezoelektrische Ladungskonstante εT Permittivität (für T = konstant) sE Nachgiebigkeits- bzw.Elastizitätskonstante (für E = konstant) FOLIE 9 GMBU 2.3 ULTRASCHALL-TECHNIK Dehnung einer ferroelastischen Keramik bei 20 kV/cm Typische Dehnung einer PZTKeramik: 0.2 % bei 20 – 30 kV/cm Parameterdefinitionen (A) Quer-/ Transversaleffekt (B) Längs-/ Longitudinaleffekt Im Bereich der Aktorik sind der piezoelektrische Transversaleffekt (d31) bzw. der Longitudinaleffekt (d33) relevant: (A) mechanische Kraftwirkung quer zum angelegten E-Feld E S 1=s11 T 1 d 31 E 3 (B) mechanische Kraftwirkung parallel zum angelegten E-Feld E S 3=s 33 T 3d 33 E 3 FOLIE 10 GMBU 2.3 ULTRASCHALL-TECHNIK Parameterdefinitionen Piezoelektrische Ladungskonstanten dij Die piezoelektrische Ladungs- oder Deformationskonstante d ist ein Maß für die induzierte elektrische Ladung bei Wirkung einer mechanischen Spannung bzw. erzielbare mechanische Dehnung bei Wirkung eines elektrischen Feldes (T=konstant). Zum Beispiel beschreibt • d33 die induzierte elektrische Verschiebungsdichte pro mechanische Spannung bzw. alternativ die induzierte Dehnung pro definiertem elektrischen Feld, jeweils in Polungsrichtung. Piezoelektrische Spannungskonstanten gij Die piezoelektrischen Spannungskonstanten g definieren das Verhältnis von elektrischer Feldstärke E zur wirkenden mechanischen Spannung T. Dividiert man die jeweiligen piezoelektrischen Ladungskonstanten dij durch die zug ij = d ij −12 8,85⋅10 gehörige Permittivitätszahl, erhält man die entsprechenden gij -Koeffizienten. 0 Zum Beispiel beschreibt • g31 das induzierte elektrische Feld in 3-Richtung bei in 1-Richtung wirkender mechanischer Spannung. FOLIE 11 GMBU 2.3 ULTRASCHALL-TECHNIK Parameterdefinitionen Elastische Nachgiebigkeit sij Die Nachgiebigkeitskonstanten s (auch Elastizitäts-Konstanten genannt) sind ein Maß für das Verhältnis der relativen Deformation S zur mechanischen Spannung T. Bedingt durch die Wechselwirkung von mechanischer und elektrischer Energie sind die jeweiligen elektrischen Grenzbedingungen zu Hinweis: berücksichtigen. Zum Beispiel beschreibt Der im englischsprachigen Raum • oftmals verwendete Young-Modul Yij entspricht dem reziproken Wert S33E das Verhältnis der mechanischen Dehnung in 3-Richtung zur in 3-Richtung des entsprechenden wirkender mechanischer Spannung, bei konstantem elektrischem Feld Elastizitätskoeffizienten. (für E = 0: Kurzschluss) Mechanische Güte Qm Die mechanische Güte Qm charakterisiert die "Resonanzschärfe" eines piezoelektrischen Körpers (Resonator) und wird vorrangig aus der 3 dBBandbreite der Serienresonanz des schwingfähigen Systems bestimmt. Der reziproke Wert des mechanischen Gütefaktors ist das Verhältnis aus Wirk- und Blindwiderstand, der mechanische Verlustfaktor tan δ. FOLIE 12 GMBU 2.3 ULTRASCHALL-TECHNIK Parameterdefinitionen Koppelfaktoren k Der Koppelfaktor k ist ein Maß für den Grad des piezoelektrischen Effektes (kein Wirkungsgrad, wie fälschlicherweise oft genannt!) Er beschreibt das Vermögen eines piezoelektrischen Materials, aufgenommene elektrische in mechanische Energie umzuwandeln und umgekehrt. Mathematisch bestimmt sich die Höhe des Koppelfaktors aus der Quadratwurzel des Verhältnisses der gespeicherten mechanischen Energie zu der gesamten aufgenommenen Energie. Unter dynamischen Bedingungen (Resonanzfall) hängt k von der entsprechenden Schwingungsform des piezoelektrischen Körpers ab. Zum Beispiel beschreibt 2 k = 2 P mech f n− f m ≈ Pel 4 fn • k33 der Koppelfaktor der Longitudinalschwingung • k31 der Koppelfaktor der transversalen Längsschwingung • kP der Koppelfaktor der Radialschwingung (planar) einer runden Scheibe • kt der Koppelfaktor der Dickenschwingung einer Platte • k15 der Koppelfaktor der Dickenscherschwingung einer Platte FOLIE 13 GMBU 2.3 ULTRASCHALL-TECHNIK Anwendung Aktoren Prinzip: Aus dem piezoelektrischen Quer- und Längseffekt ergeben sich drei verschiedene Grundelemente für piezoelektrische Aktoren: der Dickenschwinger, das Querdehnelement, der Bimorph. Hierbei ist der Bimorph eine Kombination aus zwei Querdehnelementen. Eine entgegengesetzte Ansteuerung der Elemente bewirkt eine Verbiegung des Aktors, weshalb dieser eine getrennte Bezeichnung erhält. Da der Piezoeffekt immer auf bestimmte Richtungen des Materials festgelegt ist, müssen für zwei- oder dreidimensionale Bewegungen mehrere Piezo-Elemente so kombiniert werden, Piezoaktorische Grundelemente dass sie in verschiedene Richtungen wirken. FOLIE 14 GMBU 2.3 ULTRASCHALL-TECHNIK FOLIE 15 GMBU 2.3 ULTRASCHALL-TECHNIK Anwendung FOLIE 16 GMBU 2.3 ULTRASCHALL-TECHNIK Anwendung Das dynamische Verhalten Das elektromechanische Verhalten eines zu Schwingungen angeregten piezoelektrischen Körpers lässt sich in seinen Eigenschaften mit einem elektrischen Ersatzschaltbild darstellen. C0 + C1 ist dabei die Kapazität des Dielektrikums. Die aus C, L, und R bestehende Reihenschaltung beschreibt die Änderung der mechanischen Eigenschaften, wie elastische Deformation, effektive Masse (Trägheit) und mechanische Verluste durch innere Reibung. Diese Schwingkreis-Beschreibung ist allerdings nur für Frequenzen in der Nähe der tiefsten mechanischen Eigenresonanz anwendbar. Die meisten piezoelektrischen Materialparameter werden über Impedanzmessungen an speziellen Prüfkörpern im Resonanzfall bestimmt. Einen typischen Impedanzverlauf zeigt die nebenstehende Abbildung. Für die Bestimmung bzw. Berechnung der piezoelektrischen Kennwerte werden die Serien- und Parallelresonanz herangezogen. Diese entsprechen in guter Näherung dem Impedanzminimum fm und -maximum fn. Schwingungszustände bzw. - formen werden maßgebend von Geometrie des Körpers, mechanoelastischen Eigenschaften und der Polarisationsrichtung bestimmt. Die wichtigsten Schwingungszustände an definierten Resonatoren werden mit den zugehörigen Konstanten in der nachstehenden Grafik dargestellt. FOLIE 17 GMBU 2.3 ULTRASCHALL-TECHNIK Ultraschallwandler Aufbau eines Ultraschallwandlers (Sandwich-Prinzip) Typ: DML (Double Mass Load, 2 PZT-Scheiben) Mechanische Vorspannung - Gegenlast/ Backing (Stahl) Polarisation Piezoscheiben silberbeschichtet (d≈6-7 mm) PTFE-Isolierung Frontmasse (Leichtmetall) + Aplitudenhub (10-20 µm) Amplitude Spannung Flüssigkeitslast Schwingungsmodus: Dickenschwingung (halbe Wellenlänge) Arbeitsfrequenz: 18 – 45 kHz Länge: 9 - 3,5 cm ∂2 Y ∂2 = ∂t 2 ∂ x 2 Harmonischer Oszillator x=m cos cos t c FOLIE 18 GMBU 2.3 ULTRASCHALL-TECHNIK Ultraschallwandler Mechanischer Aufbau und Kenngrößen ζ2 ζ2 2 ρm2 · c2, s2 Qm2 P ρmP · cP, sP P QmP ρm1 · c1, s1 1 Qm1 ζ1 ζ1 ρmw · cw Schallgeschwindigkeit: c Dichte: ρ Spannung: T Auslenkung: ζ akustische Impedanz: ρc akustischer Wirkungsgrad: ≈ 1− 2 k eff Q E Qm0 QE: elektrische Güte Qm0: mechanische Güte ohne Last Flüssigkeitslast akustische Intensität: I= 1 w c w f 2 2 2 FOLIE 19 GMBU 2.3 ULTRASCHALL-TECHNIK Ultraschallwandler Vorteile der DML-Wandler DML-Ultraschallwandler auf der Basis von Piezokeramikscheiben (PZT) sind im Bereich des LUS Stand der Technik. Ihre wesentlichen Merkmale sind: Sandwich-Technik: - Erhöhung der mechanischen Güte gegenüber monolithischen Transducern - Sicherstellung des Wärmeabflusses, geringere Betriebstemperaturen - Erhöhung der akustischen Abstrahlintensität durch Verwendung von Hartmetall für das Backing und Leichtmetall für das Frontelement - getrennte Anbringung von Frontmasse und Piezoelementen Vorspannung: - hergestellt durch Schrauben bzw. Flanschringe - Kontakt der Piezoscheiben auch bei maximaler Auslenkung Exzentrische Anbringung der Piezoscheiben: - Erhöhung der akustischen Intensität durch Erhöhung der Schwingungsamplitude auf der Abstrahlseite FOLIE 20 GMBU 2.3 ULTRASCHALL-TECHNIK d Leistungsanpassung von Ultraschallwandlern RLC-Ersatzschaltbild eines Ultraschallwandlers Das Ersatzschaltbild berücksichtigt das dieelektrische und mechanische A Verhalten des Wandlers: U ~ a) Piezoschwinger zT Zi C0 = Übertragungsfaktor: = C A d 2 Ae d e: piezoelektrische Spannungskonstante L C0 U ~ statische elektrische Kapazität: R Elektrik b) RLC-Ersatzschaltbild Mechanik Äquivalente elektrische Ersatzgrößen: symmetrische Anbindung der akustischen Last 2 C= K L= M 2 R= 4 2 C= K L= M 4 2 R= Zm 2 M Transducer mit Air-Backing K Zm 4 2 Rm= Zm= ρ0c0A c) Analoger mech. Schwinger FOLIE 21 GMBU 2.3 ULTRASCHALL-TECHNIK Leistungsanpassung von Ultraschallwandlern Resonanz im Transducerschwingkreis ZT = Das Modell des Transducerschwingkreises ergibt zwei klar voneinander R C j 2 LC−1 j 2 R C C 0− C 0 2 L C−1C ZT ↑ getrennte Resonanzfrequenzen: (a) parallele Resonanz fn: bestimmt durch das elektrische Verhalten von C0, C und L ωn (b) serielle Resonanz fm: bestimmt durch das mechanische Verhalten von C und L Bei fm wird die mechanisch bestimmte Impedanz minimal und die maximale Leistung kann auf die akustische Last R übertragen werden. Mit Betrachtung ωm des Resonanzfalles (ωL = 1/ ωC) und Berücksichtigung dielektrischer Ver- →f luste RD sowie interner Dehnungsverluste RS lässt sich das Ersatzschaltbild Typische Impedanzkurve eines Ultraschallwandlers Ri U ~ modifizieren. IT → I1 ↓ I3 ↓ I2 ↓ RD C0 RS R Nutzbare akustische Leistung: Pac = I 23 R applizierte Leistung: Pin = I 1 RD I 3 RS R Wirkungsgrad: (air-backed Transducer) 2 = 2 R D 0 C 0 A/4 2 R S0 C 0 A/4 2 RS RD 0 C 0 A/4 2 FOLIE 22 GMBU 2.3 ULTRASCHALL-TECHNIK Leistungsanpassung von Ultraschallwandlern Matching des Transducerschwingkreises Die maximale Leistung des Generators auf den Transducer wird übertragen, wenn: (1) die Generatorimpedanz ZG ≈ Ri und Zm= R = Ri (2) die Generatorimpedanz komplex ist und Zm= ZG* (3) wenn weder (1) noch (2) möglich sind, sollte ZG ≈ Zm angestrebt werden Ri RS U ~ L RD C0 Im vorliegenden Fall kann die Kapazität C0 durch Einfügen einer Induktanz L parallel zum Transducer eliminiert werden (Matching). R Mit Ri = Rges gilt: Ri = Mit RS = R und Ri = R D RS 0 C 0 A/4 2 RD R S0 C 0 A/4 2 2 RD R RD 2 R folgt: = RD 2R D2 R FOLIE 23 GMBU 2.3 ULTRASCHALL-TECHNIK Sonotroden Vergrößerung der Schwingungsamplituden mit Sonotroden D1 D1 D1 (a) Linear konisch einfache Herstellung, aber maximal 4-fache Vergrößerung der λ/4 Schwingungsamplitude λ/2 λ/2 (b) Exponentiell Vergrößerungsfaktor höher als bei (a) λ/4 Kostspielige Herstellung rechtfertigt Einsatz insbesondere bei Mikroapplikationen (Mikrotiterplatten) D2 D2 D2 Gestuft Exponentiell Linear konisch (c) Gestuft Potentieller Vergrößerungsfaktor auf Grund der Materialspannung in der Sonotrode auf den Wert 16 begrenzt 2 D1 = 1 D2 2 2 D 1 ≈ 1 D 2 Akustische Intensität an der Sonotrodenspitze: I ac = 1 2 2 c f 2 FOLIE 24 GMBU 2.3 ULTRASCHALL-TECHNIK Sonotroden Verlauf von Spannung und Schwingungsamplitude bei λ/2-Sonotroden verlustlose „Horn“ - Gleichung: 2 2 Spannung σ 1 ∂ 1 ∂A ∂ − − 2 =0 2 2 A ∂ x C ∂t ∂x 2 2 ∂ v 1 ∂ A ∂v v=0 ∂ x A ∂ x ∂ x C2 Amplitude ζ Spannung σ A: Querschnittsflächen Amplitude ζ v = dζ / dt Spannung σ Schwingersystem bestehend aus Transducer, Booster und Sonotrode Amplitude ζ FOLIE 25 GMBU 2.3 ULTRASCHALL-TECHNIK Sonotroden Auswahlkriterien für Sonotroden (1) Hohe dynamische Ermüdungsspannung (2) Geringer akustischer Verlust (3) Beständigkeit gegenüber Kavitationserosion (4) Chemische Beständigkeit Titan-Stahl-Legierungen haben sich auf Grund dieser Kriterien als Stand der Technik etabliert. FOLIE 26 GMBU 2.3 ULTRASCHALL-TECHNIK Sonotroden Bestimmung der abgegebenen akustischen Leistung Theoretisch: (z.B. λ/2 -Resonanz mit verlustloser exponentieller Sonotrode) * Für (D1/D2) ≠ 1 muss R durch (a) exponentiell: (D1/D2)*R (b) linear konisch: (D1/D2)*R (c) gestuft: (D1/D2)2 *R ersetzt werden. D1 D1 D1 D2 D2 D2 D1 D2 Amplitude Tranformation Strahlfläche akust. Leistung akust. Intensität (mm) (mm) (µm) (-) (cm²) (W) (Wcm-2) 37 22 24 19 9.5 3 46 72 96 3.8 6 8 2.8 0.6 0.1 69 28 95 24 44 135 exp = R D D1 /D2 R [RS D1 / D 2 R][ RS D1 / D 2 RR D ] Experimentell: (a) Kalorimetrie: Pac = U =m c P T (b) Messung der Schwingungsamplitude 1 Pac ∝ c 2 2 (c) Messung der realen Transducerleistung Pac =Pel , load −P el , unloaded (el. Leistung mit und ohne akustische Last) FOLIE 27 GMBU 2.3 ULTRASCHALL-TECHNIK Literatur [1] 3w.wikipedia.org/wiki/Piezoelektrizität [2] Piezoelektrische Fertigungstechnologie: 3w.piceramic.com [3] ENSMINGER, D. ULTRASONICS: Fundamentals, Technology, Applications 2nd ed., 1988, MARCEL DEKKER, INC. FOLIE 28 GMBU