Beugung an Spalt und Gitter

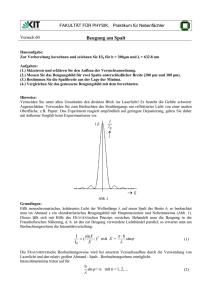
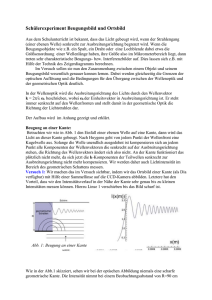
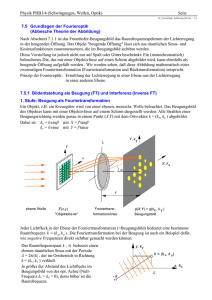
20-1
Beugung an Spalt und Gitter
1.
Vorbereitung :
Interferenz, Beugung, Huygenssches Prinzip, Kohärenz, Fresnelsche und Fraunhofersche Beobachtungsart, Beugungsbild eines Spaltes, Beugungsbild eines Gitters,
Auflösungsvermögen eines Gitterspektrometers.
Literatur :
2.
R.W. Pohl, Einführung in die Physik, Band 3
R. Fleischmann, Einführung in die Physik
Versuch :
Abb. 1 : Grundanordnung
Ein Spalt S wird durch eine Lampe L unter Zwischenschaltung einer Kondensorlinse beleuchtet und mit zwei Linsen L1 und L2 so auf einen Schirm Sc abgebildet,
daß zwischen den Linsen das Licht parallel zur optischen Achse läuft (die Abstände SL1 und L2Sc sind gleich der Brennweite der beiden Linsen f = 20 cm). Zwischen die beiden Linsen im Gebiet des Parallellichts wird das Beugungsobjekt O,
etwa der Spalt oder das Gitter, gebracht (Fraunhofersche Beobachtungsart) und
das Beugungsbild in der Schirmebene Sc mit einer Lupe beobachtet. Die Lupe
wiederum ist auf einem Mikrometerschlitten montiert, um das Beugungsbild bezüglich der Leuchtschirmkoordinate x vermessen zu können. Das Beugungsbild
des Spaltes ist in Abb. 2 skizziert.
Abb. 2 : Beugungsbild des Spaltes
20-2
Für die Minima gilt :
sin α =
Dabei bedeuten :
n⋅λ
D
.
λ = Wellenlänge
D = Spaltbreite
mit n = 1, 2, 3, ...
(1)
α = Beugungswinkel
I = Intensität
Für das Gitter erhält man ein Beugungsbild wie in Abb. 3. Für die Hauptmaxima
gilt :
sin α = ng⋅ λ .
mit n = 1, 2, 3, ...
(2)
Abb. 3 : Beugungsbild des Gitters
Die gestrichelte Einhüllende der Maxima kommt durch Beugungsphänomene an
den Einzelspalten des Gitters zustande. Das Auflösungsvermögen A = (λ/∆λ) des
Gitterspektrometers ergibt sich zu :
λ
A = ∆λ
= N ⋅n
(3)
Dabei ist N die Anzahl der Gitterstriche, n die Ordnung, in der das Spektrum beobachtet wird, λ die betrachtete Wellenlänge und ∆λ der Wellenlängenunterschied, der gerade noch aufgelöst werden kann.
3.
Aufgaben :
3.1 Herleitung
Leiten Sie die Formeln (1), (2) und (3) her.
20-3
3.2 Beugungsbild eines Spaltes
Man betrachte das Beugungsbild eines Spaltes der Breite D mit der Anordnung
von Abb. 1. Die Beleuchtung des Spaltes erfolgt mit Natriumlicht.
a)
Bestimmen Sie für D = 0.1 mm, 0.2 mm und 0.4 mm mit dem Mikrometerschlitten die Abstände ∆x des ersten, zweiten und dritten Intensitätsmaximums vom nullten Maximum. Zur Vermeidung des "toten Ganges" dreht
man den Schlitten nur in eine Richtung.
b) Die Wellenlänge von Natriumlicht soll mit Hilfe von Formel (1) abgeschätzt werden. Verwenden Sie dazu die Beziehung
sin α ≈ tan α ≈ ∆fx
(4)
wobei f2 die Brennweite der Linse L2 ist. Fehlerrechnung !
c)
Warum ist der Spalt zur spektralen Zerlegung von mehrfarbigem Licht ungeeignet ?
3.3 Beugungsbild eines Gitters
In den Strahlengang von Abb. 1 wird jetzt an Stelle des Spaltes ein Beugungsgitter
eingesetzt.
a)
Erklären Sie die Intensität der Beugungsordnungen. Schätzen Sie für das
verwendete Gitter das Verhältnis b/g (b = Breite der Gitterspalte, g = Gitterkonstante) ab.
b) Wie wirkt sich ein Verdrehen des Gitters auf das Beugungsbild aus ? Begründung !
3.4 Natriumlicht
Die Natriumdampflampe sendet Licht bei zwei benachbarten Wellenlängen λ1 =
588.997 nm und λ2 = 589.893 nm aus. In erster Ordnung können die beiden Wellenlängen mit dem verwendeten Gitter nicht aufgelöst werden und man sieht folglich nur eine Linie.
Messen Sie den Abstand ∆x der Linie in erster Ordnung von der Linie in
nullter Ordnung mit dem Mikrometerschlitten. Es sind 5 Messungen und
eine Fehlerrechnung durchzuführen !
b) Berechnen Sie mit den Meßdaten aus a) unter Verwendung von Formel (2)
und (4) die Gitterkonstante g !
a)
20-4
3.5 Bestimmung der Wellenlängen des Hg-Spektrums
a)
Messen Sie für die Quecksilberdampflampe die Abstände ∆x der Spektrallinien in erster Ordnung von der nullten Ordnung.
b) Bestimmen Sie aus (1), (4) und den Meßwerten von 3.4b) und 3.5a) die
Wellenlängen des Hg-Spektrums (zwei gelbe Linien, hellgrün, dunkelgrün,
blau, zwei violette Linien).
3.6 Auflösungsvermögen des Gitterspektralapparates
Die Formel (3) für das Auflösungsvermögen des Gitterspektralapparates soll verifiziert werden.
a)
Man bestimme die Abstände ∆x der gelben Hg-Doppellinie in drei Ordnungen bei maximaler Gitterbreite.
b) Man verringere die Gitterbreite in erster, zweiter und dritter Ordnung bis
die gelbe Doppellinie nicht mehr getrennt erscheint. Die so erhaltenen
Gitterbreiten Lm kann man durch Projektion des Gitters und eines Maßstabes bequem ermitteln.
c)
Bestimmen Sie mit den Meßwerten aus 3.6a) die Größe λ/∆λ und aus
3.6b) den Wert N ×n , wobei N = Lm/g ist. Fehlerrechnung !
Bei den jeweiligen Fehlerrechnungen ist abzuschätzen, mit welchen Fehlern die in
die Rechnung eingehenden Größen behaftet sind und wie sich diese Unsicherheit
auf die zu bestimmende Größe auswirkt.
Zusammenfassung und Diskussion.
00.Word 97