Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 7.5 Grundlagen
Werbung

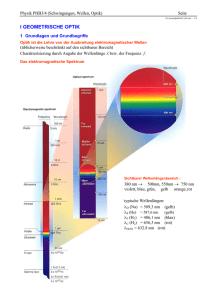
Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 1/9 7.5 Grundlagen der Fourieroptik (Abbesche Theorie der Abbildung) Nach Abschnitt 7.1.1 ist das Fraunhofer-Beugungsbild das Raumfrequenzspektrum der Lichterregung in der beugenden Öffnung. Das Objekt "beugende Öffnung" lässt sich aus räumlichen Sinus- und Kosinusfunktionen zusammensetzen, die im Beugungsbild sichtbar werden. Diese Vorstellung ist jedoch nicht nur auf Spalt oder Gitter beschränkt: Ein (monochromatisch) beleuchtetes Dia, das mit einer Objektivlinse auf einen Schirm abgebildet wird, kann ebenfalls als beugende Öffnung aufgefaßt werden.. Wir werden sehen, daß diese Abbildung mathematisch einer zweimaligen Fouriertransformation (Fouriertransformation und Rücktransformation) entspricht. Prinzip der Fourieroptik: Ermittlung der Lichterregung in einer Ebene aus der Lichterregung in einer anderen Ebene. 7.5.1 Bildentstehung als Beugung (FT) und Interferenz (Inverse FT) 1. Stufe: Beugung als Fouriertransformation Ein Objekt, z.B. ein Kreuzgitter wird von einer ebenen, monochr. Welle beleuchtet. Das Beugungsbild des Objektes kann mit einer Objektivlinse auf einem Schirm dargestellt werden. Alle Strahlen einer Beugungsrichtung werden genau in einem Punkt (X,Y) mit dem Ortsvektor k = (kx, ky ) abgebildet. Dabei ist: kx = ksin mit X = f'tan ky = ksin mit Y = f'tan Y, k y L y x X, k x f' ebene Welle E(x,y) "Objektebene" Fouriertransformationslinse g(X;Y) = g(kx , k y ) Beugungsbild Jeder Lichtfleckin der Ebene der Fouriertransformation (=Beugungsbild) bedeutet eine bestimmte Raumfrequenz k (k x , k y ) . Die Fouriertransformation bei der Beugung ist auch ein Beispiel dafür, wie negative Frequenzen direkt sichtbar gemacht werden können. Das Raumfrequenzpaar k , -k bedeutet einen ebenen räumlichen Sinus mit der Periode = 2/|k| , der im Ortsbereich in Richtung k = (kx, ky ) verläuft. Je größer der Abstand des Lichtflecks im Beugungsbild von der opt. Achse (NullFrequenz kx = ky = 0), desto höher ist die Raumfrequenz. y, ky k = (k x , k y ) x, kx -k Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 2/9 2. Stufe: Bildentstehung als Interferenz Die Lichtflecken im Beugungsbild (in der Ebene der Fouriertransformation) können als Ausgangspunkt Huygenscher Elementarwellen angesehen werden, die sich weiter ausbreiten und auf der Bildebene überlagern, d.h. interferieren. Das sich ergebende Interferenzmuster ist dann genau das Bild des Gegenstandes. f' E(x,y) "Objektebene Fouriertransformationslinse g(X;Y) = g(kx , k y ) Beugungsbild (Objektiv) "Primäres Bild" Bildebene "Sekundäres Bild" Die Objektivlinse hat damit zwei Funktionen: a) Im 1. Schritt dient sie als Fouriertransformationslinse, die das Fraunhofer-Beugungsmuster (primäres Bild) in der Ebene der Fouriertransformierten erzeugt (hintere Brennebene der Linse). b) Im 2. Schritt vermittelt Sie die Inverse Fouriertransformation (= Fouriersynthese). Die Wellen in der Transformationsebene stellen die räumlichen Spektralkomponenten dar, die sich in der Bildebene zum Bild überlagern. Die Linse als Tiefpassfilter Das Beugungsbild (= Fouriertransformierte) enthält die gesamte Bildinformation. Zur exakten Rekonstruktion sind alle Raumfrequenzen notwendig (- < kx, ky < + ). Die maximale Raumfrequenz z.B. in y-Richtung ist aber nur ky,max = k0sinmax , wobei max der maximale Beugungswinkel ist, der von der Linse noch erfaßt wird. Zu dieser Raumfrequenz gehört eine (sinusförmige) periodische Struktur mit der Periode d min 2 k y ,max 2 2 sin max sin max Konsequenzen: Die Objektivlinse wirkt wie ein Tiefpassfilter. Eine Struktur der Dimension dmin = /sinmax ist die kleinste Struktur, die auf dem Bild noch erkennbar ist. ( Auflösungsvermögen des Mikroskops) Die Kanten eines scharfkantigen Objektes werden im Bild aufgeweicht, entsprechend der Größe von dmin. Weiter erkennt man sofort die Möglichkeit in der Fourierebene mit Hilfe von Masken, Filtern, Schablonen usw., bestimmte Raumfrequenzen ganz oder teilweise auszublenden oder in der Phase zu verschieben. Die entsprechenden Verfahren heißen dann Raumfilterung, Phasenkontrastoder Schlierenmethode. Wir wollen hier das Verfahren der räumlichen Filterung skizzieren. Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 3/9 7.5.2 Räumliche Filterung (Optischer Computer) Bei der Fourieranalyse von Zeitsignalen will man häufig verdeckte periodische Signale mit kleiner Amplitude auffinden (z.B. bei Oberwellenmessungen). Das analoge Problem bei der Bildanalyse besteht darin, periodische Strukturen, die verdeckt oder sonst schlecht sichtbar sind, zu erkennen und quantitativ auszuwerten. Eine sinusförmige, periodische Struktur erscheint im Fourierspektrum als Beugungspunktepaar (Raumfrequenzpaar). Auf diese Weise können auch mehrere übereinanderliegende und visuell nicht erkennbare Periodika erkannt werden. Durch einfache Eingriffe in der Beugungsebene kann das Bild dieser periodischen Muster bei der anschließenden Rekonstruktion dargestellt werden. Die Rekonstruktion wird mit einer 2. Fouriertransformation durchgeführt, die wieder das Original herstellt. Durch entsprechende Eingriffe in die Fourierebene können gezielt Bildanteile durch Ausfilterung der zugehörigen Raumfrequenzen zum Verschwinden gebracht oder abgeschwächt werden. Ebenso können Details hervorgehoben werden, indem man nicht interessierende Bildanteile abschwächt oder löscht. Y, ky L1 L2 y x X, kx f1 ebene Welle E(x,y) "Objektebene" f 1' Fouriertransformationslinse f2 g(X;Y) = g(kx , k y ) Beugungsbild f 2' Bildebene Anwendungen:1 Nachbearbeitung und Analyse von photographischen Bildern in Medizin und Biologie (Mikroskopaufnahmen, Röntgenbilder, sonographische Bilder, elektronenmikroskopische Aufnahmen) Photographische Bildverstärkung Mustererkennung 1 Anmerkung: Bei der digitalen Bildverarbeitung werden im Prinzip die gleichen Verfahren angewandt. Hierbei muß allerdings nicht "analog" in die Fourierebene eingegriffen werden. Das Raumfrequenzspektrum wird rechnerisch aus dem digitalisierten Bild ermittelt und kann dreidimensional dargestellt werden. Die Rekonstruktion (Rücktransformation) und Darstellung geschieht ebenfalls rein rechnerisch. Da eine spektrale Filterung äquivalent zur räumlicher Faltung ist, führt eine Faltung des Bildes mit der Gewichtsfunktion zum gleichen Ergebnis. Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 4/9 Als Raumfilter werden hierbei neuerdings elektrisch ansteuerbare LCD-Modulatoren verwendet Beispiele zur räumlichen Filterung (1): Originalbild verändertes Bild Transformierte gefilterte Transformierte Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 5/9 Beispiele zur räumlichen Filterung (2): a) b) c) d) (a) Ein zusammengesetztes Lunar Orbiter Mondfoto. (b) gefilterte Version des Photos ohne horizontale Linien. (c) Transformierte (Leistungsspektrum) der Mondlandschaft. (d) Beugungsmuster nach dem Wegfiltern des vertikalen Lichtfleckmusters. (aus E. Hecht: Optik) Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 6/9 Beispiel zur digitalen räumlichen Filterung (3): (aus: Prof. Dr. Stockhausen , Digitale Signalverarbeitung) Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 7/9 7.6 Auflösungsvermögen von optischen Instrumenten Jedes von einer Linse entworfene Bild eines leuchtenden Punktes (bzw. eines parallelen Strahlenbündels für einen unendlich fernen Punkt) ist eine Beugungsfigur. Das bedeutet, dass sehr eng benachbarte Punkte eines Objektes nicht mehr getrennt abgebildet werden. Beugung bestimmt das Auflösungsvermögen von optischen Instrumenten. Die Linsenfassung wirkt auch als beugende Öffnung. Damit wird die Beugungsfigur der Lochblende mit der Linse in ihrer Brennebene abgebildet. sin 1,22 D rS f ' tan f '1,22 D D (Radius des Beugungsscheibchens) f’ 7.6.1 Rayleigh-Kriterium Die Bildpunkte (Beugungsscheibchen) der einfallenden Wellen zweier Punktlichtquellen kann man unterscheiden, wenn das zentrale Maximum der ersten Welle auf das 1. Minimum der zweiten Welle fällt , bzw. umgekehrt. Quelle 1 Quelle 2 Beugungsscheibchen der Punktlichtquellen Minimaler Winkel, unter dem zwei Objekte noch aufgelöst werden können. sin min 1,22 D Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 8/9 7.6.2 Teleskopauflösungsvermögen Die Teleskopvergrößerung kann prinzipiell beliebig groß gemacht werden. ( ' f' ' Obj' . ) f Oku . Die Grenze bildet jedoch das Auflösungsvermögen durch Beugung am Objektiv. Objektiv Okular f’Obj sin min 1,22 fOku D Der minimale Winkel, unter dem zwei weit entfernte Objekte getrennt wahrgenommen werden können, wird vom Durchmesser des Objektives und von der Wellenlänge bestimmt. 7.6.3 Mikroskopauflösungsvermögen Zur Bestimmung der Auflösungsgrenze des Mikroskops betrachten wir die Beugung am Objekt, z.B. einer Gitterstruktur. Nach Abbe müssen nämlich zur Bildentstehung möglichst viele Beugungsmaxima (= Raumfrequenzen) in das Objektiv eintreten, da die gesamte Information des Gegenstandes im Beugungsbild enthalten ist. Damit überhaupt ein Bild entsteht, muss mindestens die erste Beugungsordnung in das Objektiv eintreten. Für ein gitterartiges Objekt gilt für die 1. Ordnung: sin 1 b Befindet sich zwischen Objekt und Objektiv ein Medium mit der Brechzahl n (z.B. Dispersionsöl) ändert sich die Wellenlänge und man erhält: bmin n sin 1 Minimal auflösbare Struktur nsin heißt Numerische Apertur NA Für nsin 1 (maximal erreichbar) folgt: bmin Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 41_FourierOptik_Aufloesung_BA.doc - 9/9 7.6.4 Abbesche Mikroskoptheorie Abbe: Damit in der Bildebene ein Bild entsteht, muss mindestens die 0. und die 1. Beugungsordnung in das Objektiv eintreten. Objektebene: Gitter G Blende Bildebene B Brennebene: Beugungsbild des Objektes Abb.: Abbildung eines Gitterobjekts nach Abbe Die vom Objekt-Gitter ausgehenden Beugungsstrahlen werden in der hinteren Brennebene der Abbildungslinse (Objektiv) fokussiert. Hier entsteht das primäre Bild (FraunhoferBeugungsbild des Objekts). Im Falle eines periodischen Gitters ist das Beugungsbild ein System von hellen, diskreten Punkten, die die verschiedenen Beugungsordnungen repräsentieren. Das von den Beugungspunkten ausgehende Licht interferiert in der Bildebene zur Lichtverteilung des Bildes. Im dargestellten Beispiel werden von der Objektivöffnung die -1., 0. und +1. Beugungsordnung erfasst und in der Brennebene abgebildet. Dementsprechend ergibt sich in der Bildebene eine Intensitätsverteilung, die der Beugungsintensitätsverteilung eines Dreifachspaltes entspricht. Wie man sieht, ist die Ähnlichkeit der Bildintensitätsverteilung mit der des Objekts nur sehr gering. Im wesentlichen kann aus dem Bild in diesem Falle nur die Gitterkonstante des Objekts (um den Vergrößerungsmaßstab gedehnt) entnommen werden. Um eine größere Ähnlichkeit des Bildes mit dem Objekt zu erzielen, müssen offenbar mehr Beugungsordnungen vom Objektiv erfasst werden. Bei schiefer Beleuchtung muss das Mikroskopobjektiv die 0.te und eine 1. Ordnung erfassen. Die Auflösung bei einer Beleuchtung nach Köhler mit NAObj. = NAOku. wird daher d min 2n sin Mikroskopauflösung nach Abbe