Numerische Simulation des schlagenden menschlichen Herzens

Jülich Aachen Research Alliance
Section for High-Performance Computing
- Projekt JARA SEED Towards a Computational Model of Blood Flow in the Left Human Heart,
Aorta and Connecting Vessels
Numerische Simulation des schlagenden menschlichen
Herzens - Berechnung von Strömungsfeldern in zeitlich
veränderlichen Geometrien
Diplomarbeit
von
cand.-Ing. Stephanie Martha Schmitz
Matrikelnummer: 250952
Betreuer: Dipl.-Ing. M. Behbahani
Referent: Prof. M. Behr, Ph.D.
Aachen, den 21. August 2010
CHAIR FOR
COMPUTATIONAL
ANALYSIS OF
TECHNICAL
SYSTEMS
I
Inhaltsverzeichnis
Abbildungsverzeichnis
III
Tabellenverzeichnis
V
Symbolverzeichnis
VIII
1 Einleitung
1.1 Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Aufgabenstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 Medizinische Grundlagen
2.1 Das Herz . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Herzzyklus . . . . . . . . . . . . . . . . .
2.2 Koronararterie . . . . . . . . . . . . . . . . . . .
2.3 Blut . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.1 Aufgabe und Zusammensetzung von Blut
2.3.2 Fließeigenschaften von Blut . . . . . . . .
2.4 Hämostase . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Einfluss der Strömung auf die Hämostase
3 Grundlagen der Numerischen Simulation
3.1 Mathematische Modelle . . . . . . . . . . .
3.1.1 Modell der Blutströmung . . . . . .
3.1.2 Modell der Thrombosemodellierung
3.2 Diskretisierung . . . . . . . . . . . . . . . .
3.3 Gittergenerierung . . . . . . . . . . . . . . .
3.3.1 Elastic Mesh Update Method . . . .
4 Strömungssimulation des Herzens
4.1 Stand der Forschung . . . . . . . . .
4.2 Aufbereitung der Daten . . . . . . .
4.3 Gittergenerierung . . . . . . . . . . .
4.3.1 Elastic Mesh Update Method
4.3.2 Anfängliche Probleme bei der
4.3.3 Endgültiges Gitter . . . . . .
4.4 Strömungsberechnung . . . . . . . .
4.4.1 XNS Input . . . . . . . . . .
4.5 Simulationen . . . . . . . . . . . . .
4.5.1 Rechnung 1 - Instationär . .
4.5.2 Rechnung 2 - Stationär . . .
4.5.3 Rechnung 3 - Instationär . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
2
.
.
.
.
.
.
.
.
4
. 4
. 5
. 7
. 9
. 9
. 11
. 12
. 15
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
19
19
19
20
22
23
24
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
Gittererstellung .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
. . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
26
26
27
30
32
36
39
43
45
46
46
47
50
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Inhaltsverzeichnis
4.5.4
4.5.5
II
Rechnung 4 - Instationär . . . . . . . . . . . . . . . . . . . . . . . . 51
Rechnung 5 - Instationär . . . . . . . . . . . . . . . . . . . . . . . . 51
5 Simulation des Thrombozytenwachstums in einer Koronararterie
5.1 Stand der Forschung . . . . . . . . . . . . . . . . . . . . . . .
5.2 Arbeitsschritte . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3 Aufbau des Experiments . . . . . . . . . . . . . . . . . . . . .
5.4 Gittergenerierung - Elastic Mesh Update Method . . . . . . .
5.4.1 Anfängliche Probleme bei der Gittererstellung . . . . .
5.4.2 Endgültiges Gitter . . . . . . . . . . . . . . . . . . . .
5.5 Strömungsberechnung . . . . . . . . . . . . . . . . . . . . . .
5.6 Vorbereitung zur Berechnung des Thrombenwachstums . . . .
5.7 Berechnung des Thrombozytenwachstums . . . . . . . . . . .
5.8 Auswertung des reaktionsgesteuerten Schichtwachstums . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
55
55
55
56
57
59
59
60
65
69
72
6 Zusammenfassung und Ausblick
77
Literaturverzeichnis
80
A Anhang
A.1 Strömungssimulation der Herzgeometrien . . . . . . . . . . . . . . . . . . .
A.1.1 VRML 1.0 Format . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.1.2 XNS Input File . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.1.2.1 Verschiebung - “mshift” Input . . . . . . . . . . . . . . . .
A.1.2.2 Instationäre Rechnung . . . . . . . . . . . . . . . . . . . . .
A.1.2.3 Stationäre Rechnung . . . . . . . . . . . . . . . . . . . . .
A.2 Koronararterie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.2.1 Verschiebung - “mshift” Input . . . . . . . . . . . . . . . . . . . . . .
A.2.2 XNS Input File für die Strömungsberechnung am Bespiel der 81,90
% Stenose . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.2.3 XNS Input File für die ADR Gleichungen nach Belegung der 1.Schicht
am Beispiel der 81,90% Stenose . . . . . . . . . . . . . . . . . . . . .
A.3 Datenstruktur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.3.1 Herz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A.3.2 Koronararterie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
85
85
86
86
88
89
91
91
92
94
96
96
96
III
Abbildungsverzeichnis
1.1
Zwei der 30 extrahierten Herzgeometrien . . . . . . . . . . . . . . . . . . . .
2.1
2.2
2.3
2.4
2.5
2.6
.
.
.
.
.
4
5
6
7
8
.
9
.
.
.
.
10
11
13
14
Aufbau und Blutfluss durch das Herz [23] . . . . . . . . . . . . . . . . . .
Darstellung der Aorten- und Mitralklappe [48] . . . . . . . . . . . . . . . .
Herzzyklus, bearbeitet nach [23] . . . . . . . . . . . . . . . . . . . . . . . .
Druckdaten eines Herzzyklus (Daten nach [23]) . . . . . . . . . . . . . . .
Herzzyklus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ansicht des Herzens mit Darstellung der rechten Koronararterie und dem
hinteren absteigenden Ast der linken Koronararterie[15] . . . . . . . . . .
2.7 Koronardurchblutung: Gleichzeitige Registrierung des Durckverlaufs im linken Ventrikel, in der Aorta, in der linken Koronararterie und im Sinus coronarius (venöser Ausstrom) [22] . . . . . . . . . . . . . . . . . . . . . . .
2.8 Blutzusammensetzung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.9 Viskosität von Blut in Abhängigkeit von der Scherrate, bearbeitet nach [1]
2.10 Thrombozyt (nach Gawaz) a) in Ruhe b) aktiviert [7] . . . . . . . . . . .
2.11 Bluttfluss, Erythrozyten sammeln sich in der Gefäßmitte und es entsteht
ein mit Thrombozyten angereicherter Plasmasaum [37] . . . . . . . . . . .
2.12 von Willebrandt Faktor . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
. 15
. 17
3.1
Modell der Thrombose Aktivierung, Advektion und Aggregation [56] . . . . 21
4.1
4.2
4.3
4.4
4.5
Darstellung der verschiedenen Ebenen [42] . . . . . . . . . . . . . . . . . .
MRT Aufnahmen des Herzens in verschiedenen Ebenen . . . . . . . . . .
Extraktion der Geometrien mittels der Software Mimics . . . . . . . . . .
Rohdaten des linken Ventrikel . . . . . . . . . . . . . . . . . . . . . . . . .
Darstellung der Bewegung eines Knotens und der dazugehörigen Glättung
anhand eines willkürlichen Datensatz [17] . . . . . . . . . . . . . . . . . .
Zwei aufeinander folgende Geometrien . . . . . . . . . . . . . . . . . . . .
Abmaße des linken Ventrikels . . . . . . . . . . . . . . . . . . . . . . . . .
Topologie zweier Oberflächennetze zu unterschiedlichen Zeitpunkten [17] .
Vergleich der Gitterpunkte für zwei unterschiedliche Zeitschritte am Beispiel
des linken Ventrikels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Zwei aufeinander folgende Geometrien . . . . . . . . . . . . . . . . . . . .
Darstellung der sich überlappenden Dreiecke auf dem Oberflächengitter .
Skweness Equiangle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Darstellung der sich verformenden Elemente . . . . . . . . . . . . . . . . .
7. Geometrie der extrahierten Gitter . . . . . . . . . . . . . . . . . . . . .
Darstellung des Gitters im Schnitt . . . . . . . . . . . . . . . . . . . . . .
Geometrien 1 bis 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Geometrien 16 bis 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.16
4.17
.
.
.
.
27
27
28
29
.
.
.
.
29
30
30
31
.
.
.
.
.
.
.
.
.
.
32
35
37
38
39
39
40
41
42
43
Abbildungsverzeichnis
4.18
4.19
4.20
4.21
4.22
4.23
4.24
4.25
4.26
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5.14
5.15
5.16
5.17
IV
Herzzyklus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Residuum der instationären Rechnung; Abbruch nach 98 Schritten . . . . .
Instationäre Rechnung, Geschwindigkeiten nach 10 und nach 50 Zeitschritten
Stationäre Rechnung - Geschwindigkeiten bei einer Viskosität von 2000 und
465 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Residuum der 4. Rechnung . . . . . . . . . . . . . . . . . . . . . . . . . . .
Residuum der 5. Rechnung . . . . . . . . . . . . . . . . . . . . . . . . . . .
Auswertung des “data.bc” Files, erstellt von M. Behr . . . . . . . . . . . . .
Geschwindigkeitsprofil in der Klappenebene . . . . . . . . . . . . . . . . . .
Aufbau des Experiments [13] . . . . . . . . . . . . . . . . . . . . . . . . .
Experimentelle Ergebnisse des Thrombozytenwachstums, nach einer Zeit
von 0:06, 8:06 und 13:21 Minuten nach Begin der Strömung [4] . . . . . .
Geometrie der Stenose . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Darstellung unterschiedlicher Geometrien der Stenose . . . . . . . . . . .
Darstellung der Netzabhängigkeiten und Netzqualität
Obere Bilder: Grobes Netz
Untere Bilder: Lokal verfeinertes Netz . . . . . . . . . . . . . . . . . . . .
Darstellung des Skewness Equiangle des Gitters in verschiedenen Ebenen
parabolisches Geschwindigkeitsprofil v(r) bei laminarer Rohrströmung . .
Experimentelle Auswertung des Experiments von Ku und Flannery, bearbeitet nach [26] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Netz bei einer Stenose von 99,53 % . . . . . . . . . . . . . . . . . . . . .
Residuum der Strömungsberechnung der 78,5% Stenose . . . . . . . . . .
Unterschiedliche Stadien eines Blutplättchens [5] . . . . . . . . . . . . . .
An Kollagen adhärierte Thrombozyten [5] . . . . . . . . . . . . . . . . . .
Geometrien der unterschiedlichen Startstenosen . . . . . . . . . . . . . . .
Scherrate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Konzentration von [AP ]0 in Abhängigkeit der Scherrate . . . . . . . . . .
kaa Werte bei den unterschiedlichen Stenosen . . . . . . . . . . . . . . . .
kaa Werte aufgetragen über der Scherrate . . . . . . . . . . . . . . . . . .
44
48
48
49
50
52
52
53
53
. 56
. 57
. 58
. 58
. 59
. 60
. 61
.
.
.
.
.
.
.
.
.
.
63
64
65
68
68
70
72
73
75
76
V
Tabellenverzeichnis
2.1
Fließparameter im menschlichen Blutkreislauf [4], [37] . . . . . . . . . . . . 16
3.1
Übersicht über Vor- und Nachteile strukturierter und unstrukturierter Gitter (jeweils relativ zueinander) [46] . . . . . . . . . . . . . . . . . . . . . . . 23
4.1
4.2
4.3
XNS Input für den Verschiebungsvektor . . . . . . . . . . . . . . . . . . . . 35
Maximale Verschiebungsvektoren zwischen zwei aufeinander folgenden Netzen 36
Anzahl der Elemente und Knoten (nur space Anzahl) . . . . . . . . . . . . . 40
5.1
5.2
5.3
5.4
5.5
5.6
5.7
Anzahl der Elemente und Knoten (space) . . . . . . . . . . . . . . . . . . .
Messpunkte des Experiments von Ku und Flannery [26] . . . . . . . . . . .
Angabe der Rechnungsgrößen zu den unterschiedlichen Stenosen . . . . . .
XNS Input der ADR Gleichungen . . . . . . . . . . . . . . . . . . . . . . . .
Einfluss der Konzentration von AP am Beispiel einer 95,9% Stenose . . . .
Angabe der Rechnungsgrößen zu den unterschiedlichen Stenosen . . . . . .
Durchschnittliches Wachstum der Schichten bei den unterschiedlichen Stenosen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Angaben zur Ermittlung der benötigten Zeit für die Bedeckung einer Schicht
Angaben zur Ermittlung der Konstante kaa . . . . . . . . . . . . . . . . . .
5.8
5.9
60
63
65
66
69
71
72
74
74
VI
Symbolverzeichnis
Abkürzungen
ADP
Adenosindiphosphat
ADR
Advektion-Diffusion-Reaktion
AP
Aktivierte Thrombozyten (Activated platelets)
ASCII
American Standard Code for Information Interchange
DAP
diskrete Adhäsionspunkte
EMUM
Elastic Mesh Update Method
FDM
Finite-Differenzen-Methode
FEM
Finite-Elemente-Methode
FVM
Finite-Volumen-Methode
KV
Kontrollvolumen
LAD
Ramus interventricularis (left anterior descending coronary artery)
LCA
linke Koronararterie (left coronary artery)
LCX
Ramus circumflex (left circumflex coronary artery)
LM
Hauptstamm der linken Koronararterie (left main coronary artery)
MRT
Magnetresonanztomographie
PAF
platelet-activating factor
PDGF
platelet-derived growth factor
RCA
rechte Koronararterie (right coronary artery)
Re
Reynoldszahl
Tabellenverzeichnis
VII
RP
Ruhende Thrombozyten (Resting platelets)
VRML
Virtual Reality Modeling Language
vWF
von-Willebrand-Faktor
XNS
Executable Navier Stokes
Formelzeichen
[AP ]0
Konzentrationen der AP im Inflow
[RP ]0
Konzentrationen der RP im Inflow
α0
Kollisionseffizienz zweier aktivierter Plättchen
v̄
mittlere Geschwindigkeit
!
Deformationsgeschwindigkeitstensor
∇
Nabla-Operator
σ
Cauchy-Spannungstensor
τ
deviatorischer Schubspannungstensor
f
Volumenkräfte
I
Einheitstensor
u
Geschwindigkeitsvektor
Q̇
Einlaufvolumenstrom
η
dynamische Viskosität
λapr
Menge pro Thrombozyten freigesetzter aktivierender Substanz
λADP
Menge pro Thrombozyten freigesetztes ADP
Ω
Integrationsgebiet
·
γ
Scherrate
ρ
Dichte
τ
Schubspannung
τvs
Vergleichsschubspannung
Tabellenverzeichnis
VIII
ci
Konzentration der Spezies i
Db,i
Brownscher Diffusionskoeffizient der Spezies i
Di
Diffusionskoeffizient der Spezies i
Ds
Verstärkungsfaktor der Diffusivität der Spezies i
Ji
orts- und zeitabhängiger Strom der i-ten Spezies
js
Kollisionsrate der Thrombozyten
kaa
Adhäsionsrate eines aktivierten Plättchens in der Strömung zu einem schon
adhärierten Plättchen
kaa
Adhäsionsrate eines aktvierten Plättchens an der reaktiven Oberfläche
kpa
Grenzwert für die Thrombozytenaktivierung
krs
Adhäsionsrate eines ruhenden Plättchens an der reaktiven Oberfläche
nsd
Anzahl an Raumdimensionen (Number of space dimensions)
p
Druck
Qe
Winkel für das gleichseitige Element
Qmax
größter Winkel in der Zelle
Qmin
kleinster Winkel in der Zelle
S(x, t)
freie Oberfläche
Si
Quellterm der Spezies i
t
Zeit
V
Volumen
vmax
maximale Geschwindigkeit
A
Querschnittssfläche
D
Durchmesser
dof_1
prozentualer Anteil der freien Oberfläche an der Wand
dof_2
prozentualer Anteil der Thrombozyten in den übrigen Schichten
r
Radius
v
Geschwindigkeit
1
1 Einleitung
1.1 Motivation
In den industrialisierten Ländern stellen Erkrankungen des Herz-/Kreislaufsystems die
häufigste Todesursache dar. Im Jahre 2008 starben in Deutschland 43% der Bevölkerung
an einer solchen Erkrankung. Insbesondere bei älteren Menschen waren Herz-/Kreislauferkrankungen Todesursache Nummer eins [51]. Ursachen sind unter anderem falsche Ernährung, Stress, Rauchen und Bewegungsmangel. Durch die Zunahme des Anteils älterer Personen infolge von steigender Lebenserwartung kommt es zu einem zahlenmäßigen Anstieg
an Herzkrankheiten. Nicht immer kann durch Medikation eine Therapie erfolgen und die
Anzahl der benötigten Spenderherzen ist unzureichend. Aus diesem Grund werden mechanische Blutpumpensysteme eingesetzt. Diese lassen sich in zwei Klassen einteilen: Unterstützungssysteme und Herzersatzsysteme. Auch künstliche Herzklappen kommen häufig
zum Einsatz.
Um jedoch solche Systeme optimal entwickeln zu können ist es hilfreich die Strömungsverhältnisse im Inneren des Herzens zu kennen. Aufgrund dessen soll sich in dieser Arbeit mit
der Simulation der Verformungen und Strömungen im linken Ventrikel des menschlichen
Herzens befasst werden.
Da sich das Herz während eines Herzschlagzyklus ständig verformt, muss mit sich verformenden, komplexen Geometrien gearbeitet werden. Am Aachener Uniklinikum wurden
mittels Magnetresonanztomographie (MRT) Aufnahmen eines gesunden Patientenherz gemacht. Der gesamte Zyklus (Diastole1 und Systole2 ) wurde in 30 Bildern festgehalten. In
der Abbildung 1.1 sind zur Veranschaulichung zwei der 30 extrahierten Geometrien dargestellt. Ein Ziel dieser Arbeit ist es (siehe Kapitel 4), mit Hilfe von Verschiebungsvektoren
den sich verformenden Zyklus des Herzens durch Verwendung der extrahierten Geometrien
nachzubilden und anschließend die Strömungsphänomene soweit wie möglich zu analysieren.
Eine besonders häufige Todesursache unter den Erkrankungen des Herz-/Kreislaufsystems
ist die koronare Herzkrankheit. Bei dieser kommt es infolge verengter Herzkranzgefäße
1
2
Entspannungs- und Füllungsphase des Herzens
Anspannungs- und Auswurfphase des Herzens
1.2. Aufgabenstellung
Geometrie 7
2
Geometrie 29
Abbildung 1.1: Zwei der 30 extrahierten Herzgeometrien
zu einer Mangeldurchblutung des Herzens, welches unter anderem zu einem Herzinfarkt
führen kann [16].
Das zweite Ziel in dieser Arbeit (siehe Kapitel 5) ist die Simulation eines nahezu vollständigen Verschlusses einer Koronararterie aufgrund von Thrombenwachstum unter dem
Einfluss von hohen Scherraten zu untersuchen.
1.2 Aufgabenstellung
Die Arbeit teilt sich in zwei Teile ein. Zum einen sollen die instationären Strömungen
im linken Ventrikel des menschlichen Herzens untersucht werden, zum anderen werden die
gekoppelten Advektions-Diffusions-Reaktions-Gleichungssysteme unter Einfluss von hohen
Scherraten am Beispiel einer Koronararterie untersucht.
Im ersten Teil werden die Verformungen und Strömungen im linken Ventrikel des menschlichen Herzens untersucht. Zur Lösung der Navier-Stokes Gleichungen wird der am Institut
selbstentwickelte Finite-Elemente-basierte Strömungslöser XNS verwendet. XNS ist hochparallel und in dieser Arbeit werden die Berechnungen auf 2048 Prozessoren auf der Großrechenanlage JUGENE in Jülich durchgeführt. Bevor jedoch mit der Simulation begonnen
werden kann, wird mit der Software Pointwise ein hochaufgelöstes Volumengitter für die
erste der 30 extrahierten Geometrien erstellt. Die anschließenden Volumennetze werden
mittels der Elastic Mesh Up Methode erzeugt. Hierzu müssen Verschiebungsvektoren für
die Oberflächenknoten berechnet werden. Sind sämtliche Verschiebungen möglich und ein
kompletter Zyklus des Herzens darstellbar, kann mit der Strömungssimulation begonnen
werden. Diese soll in dieser Arbeit soweit wie möglich betrachtet werden. Bevor jedoch mit
1.2. Aufgabenstellung
3
der Simulation begonnen werden kann, müssen die Randbedingungen festgesetzt werden.
Die Auswertungen werden mit der Software Ensight durchgeführt.
Der zweite Teil dieser Diplomarbeit soll sich mit dem Einfluss von hohen Scherraten auf
das Anhaftverhalten von Thrombozyten beschäftigen. Dazu sollen die benötigten Reaktionsraten in Abhängigkeit von der Scherrate für den Verschluss einer koronararteriellen
Stenose untersucht werden. Die Randbedingungen sollen denen des Experiments von Ku
und Flannery [26] nachempfunden werden. Bei der Simulation müssen zunächst die Strömungen berechnet werden, darauf aufbauend sollen die Advektions-Diffusions-Reaktions
Gleichungen gelöst werden und die Reaktionsraten ermittelt werden. Auch hier werden die
Auswertungen mit der Software Ensight durchgeführt.
4
2 Medizinische Grundlagen
2.1 Das Herz
Das menschliche Herz (siehe Abbildung 2.1) besteht aus zwei getrennten Pumpensystemen,
welche eine identische Pumpleistung besitzen. Jedes der beiden Pumpensysteme besteht
aus jeweils einer Herzkammer (Ventrikel) und einem vorgeschalteten Vorhof (Atrium). Die
Größe des Herzens gleicht dabei ungefähr dem Anderthalbfachen der geballten menschlichen Faust. Durch Training, bzw. unter pathologischen Umständen kann seine Größe aber
erheblich zunehmen. Das Gewicht des Herzens entspricht etwa 0,5% des Körpergewichts
und beträgt durchschnittlich ca. 300 bis 350 g [48].
Aorta
V. cava superior
Pulmonalvene
linker Vorhof
Pulmonalarterie
Aortenklappe
rechter Vorhof
Pulmonalklappe
Trikuspidalklappe
Mitralklappe
linker Ventrikel
rechter Ventrikel
V. cava inferior
Abbildung 2.1: Aufbau und Blutfluss durch das Herz [23]
Das Herz besitzt die Aufgabe, das Blut durch den Körper zu pumpen und somit die Durchblutung aller Organe zu sichern. Das rechte Herz fördert dabei durch die Kontraktion des
rechten Ventrikels über die Pulmonalaterie das venöse (sauerstoffarme) Blut in den Lungenkreislauf, das linke Herz durch Kontraktion des linken Ventrikels über die Aorta das
mit Sauerstoff gesättigte Blut in den Körperkreislauf. Die Kontraktion des linken und des
rechten Herzens erfolgt dabei gleichzeitig. Aufgrund des geschlossenen Kreislaufsystems
2.1. Das Herz
5
muss die Förderleistung beider Herzen identisch sein. Das Herzzeitvolumen, also das Blutvolumen, das vom Herzen innerhalb einer bestimmten Zeit gefördert wird, beträgt rund
5 l/min, bei starker körperlicher Arbeit kann dieses auf bis zu 25 l/min erhöht werden
[23].
Der gerichtete Blutfluss wird durch die Anordnung der Herzklappen erreicht, einerseits
durch die Segelklappen (Mitral- und Trikuspidalklappe) zwischen den Vorhöfen und den
Kammern und andererseits durch die Taschenklappen (Aorten- bzw. Pulmonalklappe)
an der Grenze zwischen den Kammern und den abführenden Arterien [10]. Die Klappen
öffnen und schließen ausschließlich durch den vorherrschenden Druckgradienten zwischen
Ventrikel und Vorhof, bzw. zwischen Ventrikel und Aorten- bzw. Pulmonalarterie.
Die freien Enden der Segelklappen sind durch Sehnenfäden an den Papillarmuskeln befestigt, dadurch wird ein Zurückschlagen der Klappen während der Kontraktion verhindert.
Die Aortenklappen bestehen aus drei taschenartigen Klappen und benötigen keine zusätzliche Befestigung. Bei Druckanstieg innerhalb der Kammern weichen die Klappenränder
auseinander und das Ventil wird geöffnet [48] (Abbildung 2.2).
vorne
01.23#4.-.455%
=!&4#&)$%+)
+%>?/%#)*%+,6
-+4#,4+/%+"%
."#-%)*%+,6
-+4#,4+/%+"%
=3+/%#-.455%
@%",.%"/1#&(6
(A(/%2
9*"(6:B#$%.<
D.455%#+4#$
!"#$%&%'%!"&%()
*%+,(-%.%//
0,0
0,2
0,4
0,6
0,8
1,0
+%>?/%)*%+,6
-+4#,4+/%+"%
74&%)$%+
045"..4+21(-%.#
74&%)$%+)
045"..4+21(-%.#
."#-%)8%&%.-.455%
9:"-1(5"$4.6)3$%+
;"/+4.-.455%<
+%>?/%)8%&%.-.455%
9C+"-1(5"$4.-.455%<
hinten
(a) Darstellung des Herzens in der Klappenebene
(b) Herzklappen
Abbildung 2.2: Darstellung der Aorten- und Mitralklappe [48]
2.1.1 Herzzyklus
Die Herzfrequenz beträgt in Ruhe ca. 60-80/min, das heißt, dass in einer Sekunde ca.
die vier Aktionsphasen des Ventrikels ablaufen. Diese setzen sich aus der isovolumetrischen Anspannungs- (1) und auxotonen 1 Auswurfphase (2) und aus der isovolumetrischen
Entspannungs (3)- und Füllungssphase (4) zusammen [9]. In der Abbildung 2.3 sind die
1
Der Begriff auxoton bedeutet, dass sich während einer Kontraktion gleichzeitig die Länge und die Spannung
der Muskel ändern.
2.1. Das Herz
6
verschiedenen Phasen mit den dazugehörigen Drücken dargestellt. Ein Herzzyklus wird
dazu in Analogie zu den 30 extrahierten Herzgeometrien in 30 Zeitschritte unterteilt. Die
Systole setzt sich aus Anspannungsphase und Auswurfphase zusammen, die Diastole aus
Entspannungs- und Füllungsphase.
Da der Zyklus im linken und rechten Herz der gleiche ist und in dieser Arbeit nur der linke
Ventrikel betrachtet wird, soll der Herzzyklus hier auch am Beispiel des linken Herzens
erläutert werden.
Herzzyklus
Systole
Diastole
'#!"!
3
1
'!!"!
2
4
,-./-0
456,782.9:74
b
*(+&,)-../01
1
Anspannung, beide Klappen geschlossen
2
Austreibung, Aortenkl. geöffnet, Mitrakl. geschlossen
3
Entspannung, beide Klappen geschlossen
4
Füllung, Mitralkl. geöffnet, Aortenkl. geschlossen
1-.23
&!"!
a
%!"!
a) Öffnung der Aortenklappe
b) Schluss der Aortenklappe
c) Öffnung der Mitralklappe
d) Schluss der Mitralklappe
$!"!
#!"!
c
d
!"!
'
#
(
$
)
%
*
&
+ '! '' '# '( '$ ') '% '* '& '+ #! #' ## #( #$ #) #% #* #& #+ (!
!"#$%&'(#$$")
Abbildung 2.3: Herzzyklus, bearbeitet nach [23]
Die Anspannungsphase (1) der Systole beginnt mit dem Schluss der Mitralklappe. Diese
schließt sich, wenn der Druck im Ventrikel den des Vorhofs überschreitet. Die Aortenklappe ist zu diesem Zeitpunkt auch geschlossen (Zeitschritt 1). Anschließend kontrahiert
das Herz isovolumetrisch bis der Ventrikeldruck den Aortendruck überschreitet und die
Aortenklappe sich öffnet (Zeitschritt 3). Jetzt beginnt die Austreibungsphase (2), in der
zunächst der Druck im Ventrikel als auch in der Aorta ansteigt und ein Schlagvolumen
von ca. 80 ml in die Arterien ausgeworfen wird. Es bleibt ein Restvolumen von ca. 40 ml
im Ventrikel zurück und der Druck im Ventrikel fällt wieder unter den Arteriendruck und
die Taschenklappen schließen sich (Zeitschritt 10).
Damit beginnt die isovolumetrische Entspannung (3), bzw. Erschlaffung des Ventrikels, die
Diastole. In dieser Phase, bei der beide Klappen geschlossen sind, fällt der Ventrikeldruck
soweit ab, bis er schließlich unterhalb des Vorhofdruckes sinkt und die Mitralklappe sich
öffnet. Mit ihrer Öffnung beginnt die Füllungsphase (4) (Zeitschritt 12). Während der
Füllungsphase nimmt das Ventrikelvolumen bereits im ersten Drittel um ca. 80 % des
Schlagvolumens zu.
2.2. Koronararterie
!"#$%&&
'()"#$(%*+,-
!
1
/
2
B
8
,
9
0
!.
!!
!1
!/
!2
!B
!8
!,
!9
!0
1.
1!
11
1/
12
1B
18
1,
19
10
/.
"#$%#&'()**#+
3#456(744#+
7
.$+"/00%10
.$+"/078$0
.$+"/0#%,&($0
2(,&$%/(304115-6 9%&$:3/3:;;(04115-6 <8$&(,/3:;;(04115-6
:7;<#+=()**#&3#>??+#<@
&
A$<);(=()**#&
A$<;)(=()**#&3#456(744#+
3#456(744#+&
"#$%#&'()**#+&
3#456(744#+
&
A$<;)(=()**#&3#>??+#<@
:7;<#+=()**#&3#456(744#+
,-.!
!8-!!
92-,2
!./-/1
!!1-00
!!,-B2
!!0-12
!!,-,/
!!!-9B
09-.!
B1-!/
!2-11
9-B/
8-.,
2-0/
2-!,
/-,0
/-8.
/-2!
/-2!
/-2!
/-2!
/-8.
/-8.
/-8.
2-!,
B-!1
,-B9
,-/0
8-82
,-/0
9-,1
8-91
B-80
8-.,
8-82
,-B9
9-0!
!.-9!
!1-,.
!2-,0
!8-89
!2-./
!.-9!
0-!.
,-08
,-1.
8-91
8-2B
8-.,
8-.,
8-.,
8-.,
8-.,
8-.,
8-82
,-/0
!.-2/
!.-2/
,-08
,0-12
,9-98
,9-98
08-!!
!.9-22
!!B-.,
!!,-B2
!!8-1!
!!.-0.
!..-9B
08-/.
0,-22
08-89
02-09
0/-28
0!-B8
90-8,
99-!B
98-82
9B-/!
92-!,
9/-11
91-28
9!-B1
9.-0B
9.-/9
,0-9!
,0-12
,9-98
,9-98
Abbildung 2.4: Druckdaten eines Herzzyklus (Daten nach [23])
In der Abbildung 2.5 a) ist die zeitliche Korrelation von Druck, Volumenstrom, Ventrikelvolumen, EKG und Herztönen während eines Herzzyklus in Ruhe (Herzfrequenz 75/min)
dargestellt. Abbildung b) zeigt den Druck aufgetragen über dem Volumen des linken Ventrikels. Sein Volumen schwankt während eines Zyklus durchschnittlich zwischen den Werten 40 und 120 ml [23]. In der Abbildung ist außerdem zu erkennen, dass die Verformung
der Phasen 1 und 3 (Anspannung und Entspannung) isovolumetrisch erfolgt. In den Phasen 2 und 4 (Austreibung und Füllung) verändert sich das Volumen des Herzens allerdings
erheblich (ca. 60 ml).
2.2 Koronararterie
Als Koronararterien (oder Herzkranzarterien) werden die beiden Arterien bezeichnet ,die
das Herz kranzförmig umgeben und den Herzmuskel mit Blut versorgen oder dieses aus
ihm abführen. Die Arterien entspringen in einer linken (left coronary artery, LCA) und
einer rechten (right coronary artery, RCA) Herzkranzarterie aus der Aortenwurzel. In der
Abbildung 2.6 sind die Arterien dargestellt. Die linke Koronararterie entspringt als linker
Hauptstamm (left main coronary artery, LM) und teilt sich in den Ramus interventricularis (RIVA oder left anterior descending coronary artery, LAD) und in den Ramus
circumflexus (left circumflex coronary artery, LCX). Die rechte Koronararterie besitzt nur
einen Hauptast [39].
Durchmesser und Länge der Arterien variieren unter anderem mit der Herzgröße. Bei
einem gesunden Mann ist der Innendurchmesser des linken Hauptstammes 4,5 ± 0,5 mm.
8
p [mbar]
2.2. Koronararterie
2
Austreibung
150
1
100 Ent- 3
spannung
Anspannung
50
0
4 Füllung
60
(a) Zeitliche Korrelation von Druck,
Fluss, Ventrikelvolumen, EKG und
Herztönen während eines Herzzyklus
in Ruhe (Herzfrequenz 75/min) [23]
120
V [ml]
(b) Druck-Volumen-Diagramm
Abbildung 2.5: Herzzyklus
Die LAD ist in ihrem Anfangsteil durchschnittlich 3,8 ± 0,3 mm und nimmt bis zur
Herzspitze bis auf 1,7 ± 0,4 mm ab. LCS und RCA können an ihrem Ursprung um bis zu
1 mm variieren [39].
Der Koronarkreislauf ist ein Teil des großen Kreislaufs. Der Anteil der Koronardurchblutung bezogen auf das Herzzeitvolumen2 beträgt ca. 5%. Durch den Rhythmus von Systole
und Diastole weist die Koronarzirkulation starke Schwankungen in ihrem Blutstrom auf.
Diese Schwankungen können einmal auf die rhythmischen Pulsationen der Aorta, aber vor
allem auf die Veränderungen des interstitiellen3 Myokarddrucks4 hervorgerufen werden.
Der Herzmuskel wirkt auf die in den mittleren und inneren Wandschichten verlaufenden
Gefäße ein, wodurch der Einstrom in die linke Koronararterie zu Beginn der Systole völlig
unterdrückt wird. Erst wenn in der Diastole der Druck sinkt, kann ein Einstrom erfolgen
[39].
Der mittlere Koronarfluss beträgt ca. 70-80 ml/min pro 100 g Gewebe und kann maximal
auf das 4- bis 5-fache des Ruhewertes gesteigert werden. Abbildung 2.7 zeigt, dass der Fluss
2
Das Herzzeitvolumen ist das Blutvolumen, welches in einer Minute vom Herz in den Blutkreislauf gepumpt
wird.
3
Interstitiell bedeutet dazwischenliegend; zur Bezeichnung des Raums bzw. der Nischen zwischen den Körperzellen wird der Begriff des interstitiellen Raumes verwendet.
4
Herzmuskeldruck
2.3. Blut
9
Abbildung 2.6: Ansicht des Herzens mit Darstellung der rechten Koronararterie und dem
hinteren absteigenden Ast der linken Koronararterie[15]
in der Systole der Koronararterie erheblich absinkt, sogar unter Null, und der wesentliche
Anteil der Durchblutung in der Diastole erfolgt. In der Austreibungsphase übersteigt der
Druck des linken Ventrikels den der Aorta, d.h. der Druck im Myokard ist größer als der
treibende Druck für den Koronarfluss. Das hat zur Folge, dass der Fluss sistiert5 .
Im rechten Ventrikel liegen deutlich geringere Drücke vor, so dass der Druck in der Aorta,
also der treibenden Kraft, mit der die Koronargefäße durchblutet werden, immer höher
ist. Somit kommt es hier nicht zu einer Flussunterbrechung in der Systole. [22]
2.3 Blut
2.3.1 Aufgabe und Zusammensetzung von Blut
Das Blutvolumen im Körper eines Erwachsenen beträgt bei Frauen ca. 4 - 4,5 l, bei Männern ca. 4,5 - 5 l (ungefähr 8% des Körpergewichts). Blut besitzt vor allem die Aufgabe des
Transports zahlreicher Stoffe (O2 , CO2 ,...), des Transports von Wärme (Heizung und Kühlung), der Signalübermittlung (Hormone), sowie der Pufferung und Abwehr körperfremder
Stoffe und Mikroorganismen [9].
5
unterbrochen wird
2.3. Blut
10
Abbildung 2.7: Koronardurchblutung: Gleichzeitige Registrierung des Durckverlaufs im
linken Ventrikel, in der Aorta, in der linken Koronararterie und im Sinus
coronarius (venöser Ausstrom) [22]
Blut setzt sich zusammen aus ca. 45% festen und 55% flüssigen Bestandteilen. Die Blutzellen stellen dabei die festen Bestandteile dar, deren prozentualer Anteil im Gesamtblutvolumen als Hämatokrit bezeichnet wird. Der flüssige Anteil ist das Blutplasma, dieses
besteht zu 90% aus Wasser und zu 10% aus gelösten Substanzen und erfüllt unterschiedliche Transportfunktionen. Die zellulären Anteile des Blutes sind die roten Blutkörperchen
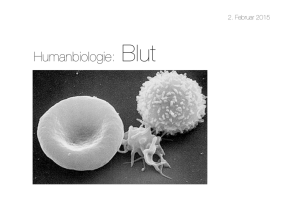
(Erythrozyten), die weißen Blutkörperchen (Leukozyten) und die Blutplättchen (Thrombozyten) [48] (siehe auch Abbildung 2.8).
Die Erythrozyten bilden mit einer Anzahl von 4,5-5 Mio/µl den größten Anteil in den
Blutzellen. Ihre Aufgabe ist der Transport von Sauerstoff und Kohlenstoff. Sie besitzen die
Form einer bikonkaven, flachen Scheibe mit einem Durchmesser von 7,5 µm und werden
im Knochenmark gebildet. Ihre Lebensdauer beträgt ca. 120 Tage [48].
2.3. Blut
11
Plasma (flüssiger Anteil)
-Wasser
-gelöste Stoffe (Plasmaproteine
nierdermolekulare Stoffe,
Elektrolyte)
Blut
Blutzellen (fester Anteil)
-Erythrozyten (rote Blutkörperchen)
-Leukozyten (weiße Blutkörperchen)
-Thrombozyten (Blutplättchen)
Abbildung 2.8: Blutzusammensetzung
Die Leukozyten besitzen mit einer Anzahl von 4000-8000/µl einen deutlich geringeren
Anteil im Blut. Sie haben die Aufgabe der allgemeinen und der spezifischen Immunabwehr
und verfügen über amöboide Eigenbeweglichkeit. Sie sind im Durchschnitt doppelt so
groß wie die roten Blutkörperchen und besitzen einen Zellkern. Die Bildung, Reifung und
Vermehrung findet in der Regel im Knochenmark statt (Ausnahme sind die Lymphozyten).
Die Anzahl der Thrombozyten beträgt ungefähr 150 000 - 350 000/µl Blut. Sie sind für
die Blutstillung und für die Bildung von Blutgerinnseln verantwortlich. Die Thrombozyten
werden im Knochenmark gebildet, besitzen keinen Zellkern und weisen einen Durchmesser
von 1-4 µm auf. Ihre Lebensdauer beträgt ca. 5-10 Tage [48].
2.3.2 Fließeigenschaften von Blut
Bei einer Flüssigkeit lassen sich die Moleküle gegenseitig verschieben, zwischen ihnen herrschen jedoch erhebliche Kräfte (Kohäsionskräfte). Die Viskosität stellt dabei ein Maß für
die Zähigkeit der Flüssigkeit dar und wird definiert durch den Reibungswiderstand, der
einer Deformation durch eine Druck- oder Schubspannung entgegengesetzt wird. Herrscht
zwischen Tangentialspannung und Geschwindigkeitsgradienten ein linearer Zusammenhang, wird von einer Newtonschen Flüssigkeit gesprochen [25].
·
Die dynamische Viskosität η wird als das Verhältnis von Schubspannung τ zu Scherrate γ
definiert:
τ
η= ·
γ
(2.1)
2.4. Hämostase
12
Aufgrund der großen Anzahl von Erythrozyten im Blut, ergibt sich eine erhöhte Viskosität
im Vergleich zu Plasma. Die komplexen mechanischen Eigenschaften der roten Blutkörperchen und ihrer Membran sind die Ursache dafür, dass Blut sich im Allgemeinen nicht
wie eine newtonsche Flüssigkeit verhält, sondern ein strukturviskoses und viskoelastisches
Verhalten aufweist.
Die Viskosität nimmt mit steigendem Hämatokritwert, bzw. mit sinkender Strömungsgeschwindigkeit zu. Die Erythrozyten können leicht verformt werden und ihr Inhalt hat eine
ähnliche Viskosität wie Plasma. Zusätzlich besitzen sie ein hohes Oberflächen/Volumen
Verhältnis. Diese Eigenschaften und die Verformbarkeit der roten Blutkörperchen haben
zur Folge, dass Blut sich mit zunehmender Geschwindigkeit weniger wie eine Zellsuspension
als vielmehr wie eine Emulsion verhält [9]. Das heißt, dass mit zunehmender Geschwindigkeit Blut sich nicht mehr wie ein Gemisch aus einer Flüssigkeit (Plasma) und einem
Feststoff (Blutzellen), sondern wie eine Zusammensetzung aus zwei Flüssigkeiten verhält.
In der Mikrozirkulation verändert sich die Blutviskosität im Vergleich zu der in größeren
Gefäßen. Beträgt der Durchmesser weniger als 1 mm, nimmt die Blutviskosität aufgrund
des Fahraeus-Lindquist-Effekts um bis zu 50% ab. Der Effekt beruht auf der Tatsache,
dass bedingt durch den geringeren Gefäßdurchmesser die Erythrozyten in eine schlangenförmige Anordnung gezwungen werden, welche von einem Plasmamantel umgeben ist.
Dieser Mantel wirkt wie eine Art Schmierfilm und begünstigt die Strömung der Erythrozyten. Die internen Reibungswiderstände der Erythrozyten untereinander fallen weg und die
Viskosität nimmt ab. Dieser Effekt kann bei der Simulation der Koronararterie vernachlässigt werden, da bei der Simulation Hämatokritwert und Viskosität konstant angenommen
werden können.
Verlangsamt sich die Strömung kommt es zu einer reversiblen Zusammenlagerung der
Erythrozyten (Rouleaux- oder Geldrolleneffekt), welches eine Erhöhung der Viskosität zur
Folge hat [18].
·
Blut kann jedoch ab einer Scherrate von γ > 100 s−1 als Newtonsche Flüssigkeit gerechnet
werden und ist dann nur noch von der Temperatur abhängig (Viskosität nimmt mit steigender Temperatur ab) [14], [32] (Abbildung 2.9). So wird bei einem Hämatokritwert von
46% und einer Raumtemperatur von 23 C◦ ein Wert von 4,7 mPas (Milli Pascalsekunde),
bei einer Körpertemperatur von 37 C◦ ein Wert von 3,6 mPas angenommen.
2.4 Hämostase
Die Hämostase ist ein Prozess, der bei der Verletzung von Blutgefäßen abläuft und einem
Blutverlust entgegenwirkt. Unmittelbar nach der Verletzung erfolgt eine Gefäßverengung
(Vasokonstriktion). Anschließend verkleben die Thrombozyten das Leck in ca. 2-4 min
2.4. Hämostase
13
!"#$%#"&'&()*+,#-
75
65
35
583
385
35
355
3555
35555
./0122,&1()34#-
Abbildung 2.9: Viskosität von Blut in Abhängigkeit von der Scherrate, bearbeitet nach [1]
(Blutungszeit) und bilden einen Blutplättchenpropf. Dieser Prozess wird auch als primäre
Hämostase (Blutstillung) bezeichnet. Bei der sekundären Hämostase, dem Prozess der
Blutgerinnung, werden die Blutplättchen aktiviert, ändern zunehmend ihre Form und
setzen in Vesikeln6 gespeicherte Stoffe frei. Dadurch wird die Bildung des eigentlichen
Thrombus (Blutgerinnsel) durch Aggregation (Zusammenkleben) eingeleitet.
Bei einer Verletzung werden subendotheliale7 Kollagenfasern freigesetzt, diese bewirken
ein Aktivieren der Thrombozyten. Aktivierte Thromobozyten können bei niedrigen Scherraten mittels Fibrinogen und bei hohen Scherraten mittels des von-Willebrand-Faktor
(vWF) anhaften. Die Adhäsion von noch ruhenden Blutplättchen an der Gefäßwand wird
als primäre Adhäsion bezeichnet, die Anlagerung von schon aktivierten Thrombozyten als
sekundäre Adhäsion [20].
Die aktivierten Thrombozyten senden jetzt unter anderem Stoffe aus, die die Adhäsion weiterer Thrombozyten fördern (Adenosindiphosphat (ADP), Thrombospondin, Fibrinogen),
aber auch solche die vasokonstriktorisch (Serotonin, platelet-derived growth factor PDGF)
wirken, den Blutstrom somit verlangsamen und die Adhäsion erleichtern. Außerdem werden verschiedene wachstumsfördernde Stoffe (PDGF und verschiedene Wachstumshormone) ausgesandt und unterschiedliche Gerinnungsfaktoren, wie Thromboxan und PAF
(platelet-activating factor) freigesetzt. Als wichtiger Thrombozyten aktivierender Faktor
ist ADP hervorzuheben. Die aktivierten Thrombozyten verändern stark ihre Form, aus
Scheiben werden Kugeln mit Pseusopodien8 , mit denen sie sich untereinander verhaken
können (Abbildung 2.10) [23].
6
Ein Vesikel ist ein rundliches bis ovales Bläschen an der Zelle, das von einer Membran umgeben ist. Vesikel
bilden somit eigene Zellkompartimente, in denen unterschiedliche zelluläre Prozesse ablaufen können.
7
Das Endothelium ist eine dünne Schicht aus Zellen der innersten Wandschicht, welche zum Gefäßvolumen
hingerichtet sind.
8
Pseudopodien, auch Scheinfüßchen genannt, sind füßchenförmige längliche, dünne bewegliche Zellfortsätze.
2.4. Hämostase
14
!"#$%&'()(*"#"
offenes kanalikuläres System
dichtes tubuläres System
+,'"-."%-/%0&'"11"'
!"#$%&'()*+,-.-/
!"#$%&'(')
01'2'2/&,
).1324&,'5&"#$&*
6"%2#$2,!*"&,
(*%23*2%"11"-+,'"
6"3*2%-7-."
83%",
612'",
4"%546"%"-+,'"
9.+'/+/&/7*+,
(((((((((().1323+.":
7,%#8"%9'."%2'0
*+,$-(./0,&1'&%0),23,$24(%5)%"
/&/7*+,(!-*#$(;8-''%<.5-,4=(!&'(
2>>&,&,(3+,+."3-.?*&,(@1'%&/'
!53%,8"(53"1
G:C+4",+%"2,
?=&2@$=90$=)"
72%"'#$&,
;,)+$%&"
C&'"3&.,(
;("2.,4,.5"'
6"3*2%-7-."
E&2*4+,"'+%"2,(!&'(F1%2'3&.&%%'
789:&";<5=:&">:(%),&9,
:"0%&'21&*5,'
A*&"'&%B-,4(C2,
)*+,-.+",$+.%''%2>>&,
!"#$%&'()*+,-.-/D
!"#$%&'(')6
01'2'2/&,D
).1324&,'5&"#$&*
Abbildung 2.10: Thrombozyt (nach Gawaz) a) in Ruhe b) aktiviert [7]
Die Blutgerinnung läuft über eine Kaskade von Reaktionen ab und hat verstärkende Wirkung. Sie kann durch eine Verletzung des Gewebes entstehen (exogener Mechanismus) oder
durch Prozesse, die auf der Innenseite eines Blutgefäßes ablaufen (endogener Mechanismus). Es kommt zu einer Aktivierung des aus den Thrombozyten oder aus dem verletzten
Gewebe freigesetzten Enzyms Thrombokinase. Dieses bewirkt in Anwesenheit von Kalziumionen die Umwandlung einer in Blutplasma gelösten Eiweißvorstufe in das Enzym
Thrombin. Dieses wiederum verursacht die Umwandlung von Fibrinogen in Fibrin. Fibrin
besteht aus Fasern, die sich miteinander vernetzen und eine Art Filz bilden können. Nach
der Gerinnung zieht sich dieser fest zusammen und bildet somit einen festen Verschluss
(Thrombus) [48], [23].
Ist die Blutung gestoppt, hat der Thrombus seine Aufgabe erfüllt und das Fibringerinnsel
muss im Verlauf der Wundheilung wieder gelöst werden. Die Fibrinolyse erfolgt durch
das Enzym Plasmin. Um einen kontrollierten Ablauf der Blutgerinnung zu gewährleisten
muss ein ständiges Gleichgewicht zwischen Aktivierung und Hemmung der Blutgerinnung
vorliegen [48].
2.4. Hämostase
15
Liegt eine koronare Herzkrankheit vor, wobei es sich um eine chronische Erkrankung des
Herzens handelt, kommt es durch arterosklerotische9 Veränderungen in den Koronararterien, zu einer zunehmenden Verengung der betroffenen Arterie. Dieses wird als Koronarstenose bezeichnet und verursacht eine Durchblutungsstörung des Herzmuskels.
2.4.1 Einfluss der Strömung auf die Hämostase
Die arteriellen Strömungszustände des Blutes variieren nicht nur in den verschiedenen Gefäßen, sondern auch innerhalb des Gefäßes. So herrscht an der Wand eine Geschwindigkeit
von Null, welche zur Gefäßmitte ansteigt und dort ihr Maximum erreicht.
Die Scherraten in Arterien sind meistens höher als in Venen und erlangen bei einem Durchmesser von 10-50 µm Werte von 500-5.000 s−1 . In Koronararterien mit 50% Stenose können
diese sogar bis auf 3.000 -10.000 s−1 steigen, bei noch höherem Stenosegrad können sogar
Scherraten von 50.000s−1 erreicht werden [37].
In der Tabelle 2.1 sind verschiedene Fließparameter innerhalb von unterschiedlichen Gefäßen im menschlichen Körpers angegeben.
Zellverteilung
Mit ansteigender Fließgeschwindigkeit im Blutgefäß konzentrieren sich die Erythrozyten
innerhalb der Mitte, so dass Plasma und Thrombozyten nach außen gedrängt werden, an
der Gefäßwand vorbeifließen und diese somit auf Defekte absuchen können (Abbildung
2.11).
Abbildung 2.11: Bluttfluss, Erythrozyten sammeln sich in der Gefäßmitte und es entsteht
ein mit Thrombozyten angereicherter Plasmasaum [37]
Arterielle Adhäsionsmechanismen
Normalerweise wären die Bluttplättchen in einer arteriellen Strömung nicht in der Lage
von alleine an der Endothelschicht anzuhaften. Die schnellströmenden Plättchen benötigen
9
Unter einer Arteriosklerose wird die Ablagerung von Fett, Thromben, Bindegewebe und Kalk in den
Blutgefäßen verstanden und bedeutet wörtlich übersetzt eine bindegewebige Verhärtung der Schlagadern.
2.4. Hämostase
16
Tabelle 2.1: Fließparameter im menschlichen Blutkreislauf [4], [37]
Durchmesser
Volumenstrom
Reynoldszahl
Mittlere Wandschubspannung
[-]
Mittlere
Wandscherrate
[1/s]
[mm]
[ml/s]
Oberschenkelarterie
5,0
3,7
280
300
11,00
Carotis
Arterie
5,9
5,1
330
250
8,90
Aufsteigende
Aorta
23-43
36
3200-6100
45-310
1,6-11
Sinus
coronarius
5,2
3,3
244
240
0,84
Hauptstamm
der linken
Koronararterie
4,0
2,9
240
500-5000
16,00
Rechte
Koronararterie
3,4
1,7
150
440
15,00
Gefäß
[Pa]
dazu das Plasmaprotein vWF. Dieses wird durch die hohen Scherraten langgestreckt und
sorgt so für mehr Bindungsdomänen. Zusätzlich können hohe Scherkräfte zu einer Selbstassoziation10 der vWF Multimere11 führen. Gleichzeitig läuft ein scherratenabhängiger
Abbau des vWF ab und stellt somit auch einen Kontrollmechanismus der Thrombogenese
dar [37], [41].
Aktivierung von Thrombozyten durch Scherbeanspruchung
Der vWF spielt somit bei der Anhaftung von Bluttplättchen unter Einfluss von hohen
Scherraten eine große Rolle. Schneider u. a. [47] nennen ihn auch “einen intelligenten
Gefäßkleber”. Nach Savage u. a. [45] ist der vWF grundlegend für die Adhäsion bei hohen Scherraten verantwortlich. In den Arbeiten von Ruggeri u. a. [40] und Reininger u. a.
[38] wird angeben, dass sich die Blutplättchen durch den vWF bei Scherraten von über
10 000 s−1 aktivieren. Die dabei erhaltenen Aggregate sind bis zu Scherraten von 20 000
10
11
Selbstassoziation bedeutet, dass die vMF Moleküle von alleine aggregieren und Multimere bilden.
Multimere bezeichnen ein aus mehreren Untereinheiten aufgebautes Molekül oder einen Molekülkomplex.
2.4. Hämostase
17
s−1 instabil, erst danach wird der vWF langgezogen und sorgt für eine stabile Anhaftung der Thrombozyten. Auch in der Arbeit von Schneider [47] ist der vWF bei hohen
Scherraten für die Bindung der Blutpättchen, insbesondere unter hohen Blutflussgeschwindigkeiten, verantwortlich. Denn nur dieser ist in der Lage, bei den hohen Scherraten wie
sie im arteriellen Gefäßsystem vorliegen, Thrombozyten zu binden. Die Ursache dafür liegt
in der Form des vWF. Bei niedrigen Scherraten liegt dieser in knäuelartiger Form (siehe
Abbildung 2.12 a)) vor und bietet somit nur wenige Bindungsmöglichkeiten. Bei hohen
Scherraten jedoch streckt er sich zu einem Faden (siehe Abbildung 2.12 b)), so dass an
ihm viele Thrombozyten anhaften können.
(a)
(b)
Abbildung 2.12: von Willebrandt Faktor
At shear rates ! <1000s-1 platelet adhesion is
mediated
by fibrinogen.
Schneider
[2]des
showed
In der Arbeit
von
[47] wird
jedoch
der
Übergang
vWF fürthat
Vollblut in
At Schneider
shear rates
! <1000s
-1 platelet adhesion is
−1
at ! Zustand
>1000s
-1 vWf
begins
to von
unfold
a coiled
den gestreckten
schon
abfibrinogen.
einer
Scherrate
1000 sfrom
angegeben.
Dies that
ist auch
mediated
by
Schneider
[2] showed
a Arteriolen
linear state
(right). Itvorliegt
thenund
becomes
der Bereich(left)
der into
und Kapillaren
bei denenthe
eine erhöhte
at !den
>1000s
-1 vWf begins to unfold from a coiled
predominant
adhesion
mediator.
vWf
can
adhere
vWF Aktivität aufgrund mechanischer Beanspruchung der Gefäßwand lebensnotwendig
(left) to a linear state (right). It then becomes the
to surfaces
both
forms
in the stretched
ist. Zusätzlich
wird in der in
Arbeit
gezeigt,
dassbut
mit only
der zunehmenden
predominant
adhesion
mediator.
vWf canAktivierung
adhere des
linear
state
enough
binding
sites
become
exposed
vWF seine Bindefähigkeit steigt [47].
to surfaces in both forms but only in the stretched
for massive platelet adhesion to take place.
linear
enoughnicht
binding
become
exposed
Die Thrombozyten
haftenstate
bei Erstkontakt
mit dersites
gesamten
flach anliegenden
Memfor
massive
platelet
adhesion
to
take
place.
bran an, sondern nur über diskrete Adhäsionspunkte (DAP), die sich in Abhängigkeit
von der Scherbelastung ausbilden. Durch diesen Mechanismus scheinen die Thrombozyten
gegen ein Fortreißen durch die Strömung gesichert zu sein. Durch die hohen Scherraten
werden weitere Rezeptoren aktiviert und somit zusätzliche Bindungen ermöglicht. Die
Thrombozytenaggregate werden außerdem, bei Ablauf der Gerinnungskaskade, durch ein
Fibrinetzwerk gegen die hohen Scherkräfte gesichert [37].
Ku und Flannery [26] fanden in ihren Untersuchungen heraus, dass eine lineare Abhängigkeit zwischen der Ablagerung von Thrombozyten an der Wand und der Scherrate vorliegt.
Steigt die Scherrate an, nimmt auch der Thrombozytenbewuchs deutlich zu.
Mit dem Einfluss der Scherraten auf die Aktivierung der Thrombozyten beschäftigen sich
Holme u. a. [44]. In ihrer Arbeit stellen sie fest, dass ab einer Scherrate von 10 500 s−1
2.4. Hämostase
18
eine signifikante Plättchenaktivierung und Formation von Mikropartikeln zu erkennen ist.
Bei physiologischen Scherraten (420 s−1 ) oder in Arterien mit geringer Stenose (2600 s−1 )
hingegen treten diese Effekte nicht auf. Ob es sich dabei in den Experimenten um eine
mit oder ohne Kollagen beschichtete Oberfläche handelt, besitzt auf die Ergebnisse keinen
signifikanten Einfluss. Auch wird in der Arbeit angeführt, dass nicht nur die Scherrate,
sondern auch die Geometrie der Stenose für die Aktivierung der Thrombozyten verantwortlich ist.
Die Verweilzeit der Thrombozyten in der Stenose liegt bei hohen Scherraten nur noch im
µs Bereich. Die damit einhergehende kurze Kontaktzeit mit der thrombogenen Oberfläche
spricht dafür, dass bei hohen Scherraten weniger Thrombozyten anhaften können.
19
3 Grundlagen der Numerischen Simulation
In dieser Arbeit soll die Durchströmung des linken Ventrikels des menschlichen Herzen, als
auch das Thrombosewachstum in einer Koronararterie mit Hilfe von numerischen Simulationen berechnet werden. Die Strömungen werden dazu mit Hilfe von partiellen Differentialgleichungen beschrieben (Abschnitt 3.1). Diese können aber, mit Ausnahme einiger
Sonderfälle, nicht analytisch gelöst werden. Um sie numerisch lösen zu können, muss eine
Diskretisierungsmethode angewendet werden, welche die Differentialgleichungen mit einem System algebraischer Gleichungen approximiert [12] (Abschnitt 3.2). Die diskreten
Punkte, an denen die Variablen berechnet werden sollen, werden durch ein numerisches
Gitter definiert, welches eine diskrete Darstellung des geometrischen Gebietes darstellt.
(Abschnitt 3.3). Da es sich sowohl bei der Simulation der Strömungen im Herzen, als auch
bei der Simulation des Thrombosewachstum, um sich verformenden Gitter handelt, wird
die Elastic Mesh Up Methode benötigt (Abschnitt 3.3.1).
3.1 Mathematische Modelle
3.1.1 Modell der Blutströmung
Die Eigenschaften des Bluts, insbesondere die Viskosität sind temperaturabhängig, in dieser Arbeit werden isotherme Zustände vorausgesetzt.
Blut wird in dieser Arbeit als viskoses, inkompressibles und isothermes Fluid betrachtet.
Die Mehrphasigkeit des Blutes wird in der Strömungssimulation vernachlässigt und wird
als Einphasenfluid angenommen. Die Fluidströmung wird durch die Navier-Stokes Gleichungen wiedergegeben. Diese Gleichungen beschreiben die Erhaltung von Masse, Impuls
und Energie, wobei das Fluid als Kontinuum angenommen wird. Da adiabate Zustände vorausgesetzt werden, muss die Energiegleichung folglich nicht gelöst werden. Für die
Blutströmungen lauten die inkompressiblen Navier-Stokes Gleichungen für die drei Geschwindigkeitskomponenten u(x, t) und den Druck p(x, t):
!
∂u
ρ
+ u · ∇u − f
∂t
"
− ∇ · σ(u, t) = 0 in Ω
(3.1)
3.1. Mathematische Modelle
20
∇·u = 0
in Ω
(3.2)
mit ρ als Dichte und f als Summe der äußeren Kräfte. Durch Ω wird das räumliche begrenzte Integrationsgebiet, bzw. der betrachtete Bereich der Strömung bezeichnet. Da das
Blut hier als newtonsches Fluid betrachtet wird, lässt sich der Cauchy-Spannungstensor
σ folgendermaßen schreiben:
σ(u, p) = −pI + τ ,
(3.3)
τ = 2η!(u),
(3.4)
!(u) =
$
1#
∇u + (∇u)T
2
(3.5)
mit η als dynamischer Viskosität, I als Einheitstensor, τ als deviatorischer Schubspannungstensor und !(u) als Deformationsgeschwindigkeitstensor.
3.1.2 Modell der Thrombosemodellierung
Die Gleichungen für die Thrombosesimulation sind in dem Strömungslöser XNS bereits
implementiert [56], [53] und wurden in Anlehnung an ein Modell nach [50] modifiziert.
Das Modell beinhaltet die Anhaftung von ruhenden (RP - resting platelets) und aktivierten (AP - Activated platelets) Plättchen an Oberflächen, die Plättchen - Plättchen
Adhäsion und sowohl die Stimulatorenausschüttung, als auch die Aktivierung ruhender
Plättchen, die einer erhöhten ADP (Adenosindiphosphat) Konzentration ausgesetzt sind
(siehe Abbildung 3.1). Für die Bestimmung der benötigten Werte wurde auf empirische
Untersuchungen zurückgegriffen.
Bei dem Modell wird davon ausgegangen, dass die plasmatische Gerinnungskaskade nicht
stattfindet, wie im Falle von mit Citrat versetztem Blut. Citrat besitzt eine gerinnungshemmende Wirkung und hat zur Folge, dass nur ADP als einziger Plättchenaktivator
bei der Simulation betrachtet werden muss. Die Experimente von Bark [4] und Flannery [13], mit denen die Simulation verglichen werden soll, wurden allerdings mit Heparin
versetztem Schweineblut durchgeführt. Dieses besitzt nicht die gleichen Wirkungen wie
Citrat. Bei dem Vergleich der numerischen mit den experimentellen Ergebnissen, muss
dies berücksichtigt werden. Dies wird in Kapitel 5.3 diskutiert.
Die Simulation der Adhäsion und Aggregation der Thrombozyten erfolgt unter Verwendung der ADR (Advektions-Diffusions-Reaktions) Gleichungen:
∂ci
+ (u · ∇)ci = ∇ · (Di ∇ci ) + Si
∂t
(3.6)
3.1. Mathematische Modelle
21
2.2 Platelet adhesion, activation and aggregation
AP
agg
rega
tion
AP
AP
n
tivatio
ac
ion
adhe
s
+ ac
n
sio
sion
he
adh
e
ad
RP
tiva
tion
AP
reactive wall
Figure 2.1: Model: Platelet activation, adhesion and aggregation
Abbildung 3.1: Modell der Thrombose Aktivierung, Advektion und Aggregation [56]
2.2.1 Governing
Dabei entspricht
ci = ci (x,equations
t) der Konzentration der jeweiligen Spezies, ∇u dem Geschwindigkeitsvektor des Strömungsfeldes, Di der Diffusivität im Medium und Si stellt den entThe generalized advection-diffusion-reaction (ADR) equation describes the transport of
sprechenden
Quellterm
dar. Dieser
und Abnahme
der
species
i in a bounded
domain erfasst
Ω ⊂ Rnsddie
dueZuto advection,
diffusionder
and Konzentration
reaction. It
reads
as
jeweiligen Spezies.
Die entsprechenden
∂ci Quellterme können folgendermaßen angegeben werden:
∂t
+ (u · ∇) ci = ∇ · (Di ∇ ci ) + S i ,
SRP = −kpa [P R]
(2.16)
where ci = ci (x, t) refers to the concentration of species i, u is the known velocity field
α0 (enhanced)
of the surrounding fluid, S
DAP
RRBC
diffusivity of species i
i = D
=i (γ̇,
kpaHct,
[RP
] −) is the
js [AP ]2
2
and S i represents a reaction term for species i, describing
their creation and destruction.
(3.7)
(3.8)
SADP = λofADP
kpaplatelets
[RP ] [RP], activated platelets [AP]
(3.9)
Writing (2.16) for the concentrations
resting
and one platelet-released agonist [a pr ] with the abbreviation [ i ] := ci leads to a system
of partial differential equations, where the several equations are mutually coupled by
Mit kpa alstheReaktionsrate
die Aktivierung der ruhenden Plättchen aufgrund der lokal
reaction terms S für
i.
erhöhten ADP Konzentration, α0 der Adhäsionseffizienz zweier aktivierter Plättchen, js
der Kollisionsrate der Thrombozyten und λADP als Konstante für die Menge an APD, die
13
von den Thrombozyten während der Aktivierung ausgeschüttet wird.
Die Diffusivität für Thrombozyten wird folgendermaßen berechnet:
Di = Db,i + Ds
(3.10)
Dabei stellt Db,i den Brownschen Diffusionskoeffizienten der jeweiligen Spezies dar und
Ds den Verstärkungsfaktor infolge des Einflusses der Erythrozyten (siehe dazu auch [8]).
3.2. Diskretisierung
22
Zur Schließung der Gleichungen und Lösung der Menge der adhärenten Thrombozyten
werden folgende Randbedingungen benötigt:
JRP (x, t) = S(x, t)krs · [RP ]
(3.11)
JAP (x, t) = S(x, t)kas + (1 − S(x, t))kaa · [AP ]
(3.12)
Japr (x, t) = −λapr S(x, t)krs · [RP ]
(3.13)
Ji stellt dabei den orts- und zeitabhängigen Strom der i-ten Spezies an einer thrombogenen
Oberfläche dar, ki ist die Reaktionsrate als Maß für die Reaktivität der Oberfläche und
S(x, t) stellt die von [50] definierte freie Oberfläche dar.
Weitere Informationen und detaillierte Erklärungen können in Waluga [56] nachgelesen
werden.
3.2 Diskretisierung
Um die partiellen Differentialgleichungen numerisch lösen zu können, müssen diese diskretisiert werden. Dabei gibt es verschiedene Diskretisierungsmethoden, welche die partiellen
Differentialgleichungen mit einem System algebraischer Gleichungen approximieren. Die
Diskretisierung erfolgt, indem Raum und/oder die Zeit durch ein Rechengitter in endlich
viele Teile zerlegt werden und die Differentialgleichungen an diesen diskreten Stellen gelöst
werden. Es existieren verschiedene Möglichkeiten zur Diskretisierung, die wichtigsten sind:
Die Finite-Differenzen- (FD), die Finite-Volumen (FV) und die Finite-Elemente-Methode
(FE).
Der Strömungslöser XNS verwendet die Finite Elemente Methode (FEM) nach Galerkin.
Diese Methode ist in der Strömungsmechanik sehr verbreitet und kann bei unstrukturierten Netzen angewandt werden. Die Gebiete oder Zellen werden als Elemente bezeichnet,
die Netzpunkte als Knoten. Die FEM nach Garlerkin benutzt das Verfahren der gewichteten Residuen [34], bei der das resultierende Residuum einer Näherungslösung minimiert
wird. Die Differentialgleichungen werden dabei mit Ansatzfunktionen multipliziert und
über das Berechnungsgebiet Ω integriert.
Als weiterführende Fachliteratur zu dem Thema wird auf Donea und Huerta [11] und
Hughes [19] verwiesen.
3.3. Gittergenerierung
23
3.3 Gittergenerierung
Bei der Berechnung von Strömungen spielt das Gitter eine entscheidende Rolle, denn die
zu berechnenden diskreten Punkte werden durch dieses definiert. Die Genauigkeit der
Rechnung hängt also unter anderem von dem verwendeten Netz ab. Dabei muss zwischen
gewünschter Genauigkeit und benötigter Rechenzeit, bzw. Speicherbedarf abgewägt werden. Denn je mehr Knoten das Netz enthält, desto mehr Zeit und Speicherplatz wird
für die Rechnung benötigt. Normalerweise wird das Gitter solange verfeinert, bis keine
Änderungen in der Strömung mehr auszumachen sind.
Bei den Gittern entscheidet man zwischen strukturierten, unstrukturierten und hybriden1
Gittern. In dieser Arbeit werden unstrukturierte Gitter verwendet, welche mit der Software Pointwise (Version 16.0.2.3) erzeugt werden. Diese besitzen den Vorteil, dass sie sich
am besten an eine beliebige Geometrie anpassen lassen. Die Elemente im Kontrollvolumen
(KV) können jegliche Form und Anzahl an Nachbarelementen und - punkten aufweisen.
Im 3D-Fall werden für unstrukturierte Gitter meistens Tetraeder und für strukturierte
meistens Hexaeder verwendet. Nachteil der unstrukturierten Gitter ist ihre komplexe Datenstruktur. Neben den Koordinaten der Gitterpunkte, müssen für unstrukturierte Gitter
auch die Nachbarschaftsbeziehungen zu den benachbarten Gitterzellen mittels aufwendiger
Datenstrukturen gespeichert werden [46]. In der Tabelle 3.1 sind die Vor- und Nachteile
strukturierter und unstrukturierter Gitter dargestellt.
Tabelle 3.1: Übersicht über Vor- und Nachteile strukturierter und unstrukturierter Gitter
(jeweils relativ zueinander) [46]
Eigenschaft
1
struk.
unstrukt.
Modellierung komplexer Geometrien
-
+
Lokale (adaptive) Gitterverfeinerung
-
+
Automatisierung der Gittererzeugung
-
+
Rechenzeit zur Erzeugung des Gitters
+
-
Programmieraufwand
+
-
Datenspeicherung
+
-
Lösung des Gleichungssystems
+
-
Parallelisierung und Vektorisierung des Lösers
+
-
Ein hybrides Gitter stellt eine Kombination aus strukturierten und unstrukturierte Gittern dar.
3.3. Gittergenerierung
24
3.3.1 Elastic Mesh Update Method
Um bei Strömungsberechnungen mit sich verformenden Geometrien arbeiten zu können,
wird die Elastic Mesh Update Method (EMUM) benötigt. Um mit der EMUM arbeiten
zu können, wird ein Verschiebungsvektor benötigt. Dieser bestimmt die Verschiebung der
Oberflächenknoten und muss, je nach Problemstellung, auf unterschiedliche Weise berechnet werden. Die in dieser Arbeit benötigten Verschiebungsvektoren und deren Erstellung
sind im jeweiligen Kapitel der Strömungsberechnung beschrieben (Kapitel 4.3.1 und 5.4).
XNS berechnet anschließend mit diesen die Knoten- und Elementenverschiebung im Inneren des Netzes.
Bei der Verformung des Gitters kann es zu einem Tangling des Netzes bekommen. XNS
detektiert ein Tangling Problem durch die Berechnung der Jakobi Determinate. Tangling
tritt dann auf, wenn die Determinante für zwei beliebige Elemente ein unterschiedliches
Vorzeichen aufweist. Die Rechnung wird daraufhin abgebrochen und XNS gibt folgende
Ausgaben:
mxyz.tangled
data.tangled
Tritt Tangling auf, muss die Stelle des Gitters und das zugehörige Element untersucht
werden, um die Ursachen für den Abbruch der Rechnung herauszufinden und das Problem
lösen zu können. Die Koordinaten für das Element, welches für den Abbruch verantwortlich
ist, können im Output File der Rechnung nachgelesen werde. Die Fehlermeldung sieht
folgendermaßen aus:
checkx: mesh is tangled
checkx: jacobian range is (-0.15212D-04, 0.30388D+02)
checkx: odd jacobian near ( 0.16541D+03,-0.15230D+03, 0.15765D+02)
Bei Verwendung der EMUM, können verschiedenen Einstellungen vorgenommen werden.
Der erste Parameter ist die Poisson Zahl (Poisson Ratio) λ/µ, welche mit dem Keyword
“mesh_ratio” aufgerufen wird und das elastische System beeinflusst. Der zweite Parameter, zur Beeinflussung der Materialeigenschaften, ist die Jakobi Determinante f und wird
dem Keyword “mesh_fraction” gesteuert. Sind keine Werte gesetzt werden standardmäßig
die Werte 1 und 0 verwendet.
Je kleiner die Poisson Zahl gewählt wird, desto größer wird der Widerstand des Materials
gegenüber Scherung. Die Poisson Zahl kann in einem Bereich von 0 und 8 liegen, die Jakobi Determinante kann in einem Bereich von 0 bis 1 gewählt werden. Je kleiner f gewählt
wird, desto kleiner wird der Einfluss der Jakobi Determinante auf das Gleichungssystem
und der Einfluss der kleineren Elemente wird im Verhältnis zu den großen Elementen grö-
3.3. Gittergenerierung
25
ßer. Wenn f=0 ist, wird die Integralform durch die Elemente der Jakobi Matrix dividiert
[6].
Da bei den vorherigen Netzen keine Verbesserung durch unterschiedliche Parameter zu
erkennen war, wurde bei dieser Arbeit bei dem endgültigen Netz nicht mit der Variation
der Parameter gearbeitet.
26
4 Strömungssimulation des Herzens
4.1 Stand der Forschung
In der Literatur gibt es viele Ansätze zur Modellierung des Herzzyklus. Mit der Füllungsphase des linken Ventrikel (Diastole), welche eine besonders wichtige Rolle im Herzzyklus
darstellt (Mandinov u. a. [30], Vasan und Levy [54]) und eine große Dynamik in der Fluidströmung aufweist, beschäftigten sich verschiedene Studien. Experimentell untersuchten
diese Steen und Steen [52], numerische Resultate liegen von Vierendeels u. a. [55] und
Baccani u. a. [2], [3] vor. Diese betrachteten allerdings nur ein achsensymmetrisches Modell. Das achsensymmetrische Modell kann genutzt werden um erste Erkenntnisse von der
Strömung zu gewinnen, stellt aber keine realistische Interpretation dar.
Dreidimensionale numerische Untersuchungen, mit unterschiedlichen Ansätzen wurden unter anderem von Saber u. a. [43], Lemmon und Yoganathan [27], Kilner u. a. [21], Long
u. a. [28], Pedrizzetti und Domenichini [35] und Oertel u. a. [33] durchgeführt. Durch diese
dreidimensionlen Untersuchungen können die Strömungen im Herzen wesentlich genauer
untersucht werden.
Mit der Interaktion von Struktur und Strömung des Herzens beschäftigten sich als eine
der ersten Forschergruppen McQueen und Peskin [31]. Weitere Modelle wurden unter
anderem von Lemmon und Yoganathan [27] und Vierendeels u. a. [55] entwickelt. Die
Verbindung von Strömung und der mechanischen Struktur des Herzmuskels erfolgt bei
all diesen Untersuchungen durch den Druck. Allerdings basieren die Modelle auf in vitro
Versuchen mit Tierherzen oder simplifizierten Modellen, so dass die Resultate nicht ohne
weiteres auf das Herz übertragen werden können.
Ein besonders weit entwickeltes Modell stammt von Oertel u. a. [33]. Diese untersuchten
in ihrer Arbeit das linke Ventrikel des menschlichen Herzen. Die benötigten Geometrien
werden dabei, wie auch in dieser Arbeit, aus MRT Daten extrahiert. Für den Herzmuskel verwenden sie ein Modell aus Faserverbund, welches die Interaktion von Fluid und
Struktur zu simulieren ermöglicht. Der Einfluss der Herzklappen wird nicht vernachlässigt,
sondern durch Verwendung von Widerständen, die zwischen 0 und ∞ variieren können,
berücksichtigt.
4.2. Aufbereitung der Daten
27
4.2 Aufbereitung der Daten
Ein gesundes Patientenherz wurde am Aachener Uniklinikum mittels Magnetresonanztomographie (MRT) in drei Ebenen (sagittale, axiale und koronale) aufgenommen (Abb.
4.1).
Koronale Ebene
Sagittale Ebene
Axiale Ebene
Abbildung 4.1: Darstellung der verschiedenen Ebenen [42]
In jeder dieser Ebenen wurde das Herz in 68 Schnittebenen unterteilt, von denen jeweils
eine Aufnahme erstellt wurde (Abbildung 4.2). Der gesamte Zyklus des Herzens (Systole
und Diastole) wurde in 30 Bildern erfasst.
(a) Sagittale Schnittebene des Herzens
(b) Koronale Schnittebene des Herzens
Abbildung 4.2: MRT Aufnahmen des Herzens in verschiedenen Ebenen
Die dabei erhaltenen 2D-Bilder wurden anschließend am Helmholtz Institut für angewandte Medizintechnik [17] mittels des Programms Mimics in 3D-Daten umgewandelt. Bei der
Erstellung der dreidimensionalen Daten wurde nur die sagittale Ansicht verwendet, aus
4.2. Aufbereitung der Daten
28
diesem Grund beträgt die Auflösung in den beiden anderen Ansichten 68 Punkte (siehe
Abbildung 4.3 a)). Abbildung 4.3 b) zeigt die Gesamtextraktion der Herzgeometrie.
68 Punkte
(koronale Ebenen)
68 Punkte
(axiale Ebenen)
(a) Sagittale Ebene
(b) Extraktion der Gesamtherzgeometrie
Abbildung 4.3: Extraktion der Geometrien mittels der Software Mimics
Die gewonnenen dreidimensionalen Rohdaten werden zunächst geglättet, um einer natürlichen Herzgeometrie näher zu kommen (Abbildung 4.4 a)). Da bei den MRT Aufnahmen
die Aortenklappe und die Mitralklappe nur schlecht zu erkennen sind, müssen diese mit
Hilfe von typischen Geometrien definiert werden (Abbildung 4.4 b)). Die Ebenen der Klappenöffnungen werden dazu vorher in den MRT Bildern festgehalten, um deren Position
bestimmen zu können (Abb. 4.2 a)) und dadurch eine gleichmäßige Bewegung der Ebenen
zu erhalten. Anschließend werden die Geometrien, also Klappen und Ventrikel, miteinander verschmolzen.
Zum Schluss erfolgt ein Verfahren zur Glättung der Geometriebewegung. Dazu werden die
sich zeitlich verändernden Koordinaten eines Knotens über die verschiedenen Geometrien
extrahiert, um anschließend die daraus erhaltene Bewegung zu glätten und somit neue
Koordinaten zu erzeugen (siehe Abbildung 4.5). Dieses Verfahren hat zur Folge, dass die
durch MRT Messungen erfassten Daten nicht mehr eins zu eins abgebildet werden. Da
die durch die Messungen erhaltenen Daten aber durchaus Ungenauigkeiten aufweisen und
physiologisch eine sprunghafte Bewegung der Knoten nicht erklärbar wäre, ist es durchaus
sinnvoll diese Glättung durchzuführen. Zusätzlich ist durch die Glättung der Koordinaten
die Anzahl der Geometrien des linkes Ventrikels nicht mehr auf die 30 MRT Aufnahmen
limitiert, sondern nun beliebig.
4.2. Aufbereitung der Daten
(a) Rohdaten des linken Ventrikels
29
(b) Extraktion
Geometrie
der
Abbildung 4.4: Rohdaten des linken Ventrikel
Abbildung 4.5: Darstellung der Bewegung eines Knotens und der dazugehörigen Glättung
anhand eines willkürlichen Datensatz [17]
In der Abbildung 4.6 sind in Bild a) zwei aufeinander folgende Geometrien vor und in
Abbildung b) nach der Glättung zu erkennen. Hierbei wird deutlich, dass sich die Verschiebung deutlich verkleinert hat und keine sprunghafte Bewegung mehr statt findet.
Bei der Erstellung der Geometrie des Ventrikels wird nur die äußere Form mit einer glatten
Oberfläche dargestellt. Das Innere des Ventrikels wie zum Beispiel Papillarmuskel, Sehnenfäden der Mitralklappe und sonstige Unebenheiten werden nicht aus den MRT Daten
extrahiert und somit auch nicht bei der anschließenden Simulation berücksichtigt.
4.3. Gittergenerierung
(a) Vor der Glättung der Daten
30
(b) Nach der Glättung der Daten
Abbildung 4.6: Zwei aufeinander folgende Geometrien
In der Abbildung 4.7 sind verschiedene Maße des linken Ventrikels dargestellt um sich eine
Vorstellung über dessen Größe machen zu können.
(a)
(b)
Abbildung 4.7: Abmaße des linken Ventrikels
4.3 Gittergenerierung
Die Vernetzung des Herzens erfolgt in zwei Schritten. Das Oberflächenetz wird vom Helmholtz Institut [17] zur Verfügung gestellt. Dieses wird erstellt, indem die aus den 30 MRT
Aufnahmen extrahierten Geometrien vernetzt werden. Die Oberfläche des Herzens wird
dabei durch Vierecke vernetzt, welche anschließend diagonalisiert werden, um Dreiecke zu
4.3. Gittergenerierung
31
erhalten. Diese werden benötigt damit das Volumengitter aus Tetraedern erstellt werden
kann.
Die Schwierigkeit bei der Erstellung der Oberflächennetze besteht darin, dass die Oberflächentopologie immer die gleiche bleiben muss. Das heißt, dass bei der Vernetzung gewährleistet sein muss, dass die Anzahl und Nummerierung der Knoten und Elemente sich nicht
ändert. Denn für den Strömungslöser XNS ist bei der Erstellung von den Volumengittern
eine einheitliche Topologie der Oberflächennetze unabdinglich. In der Abbildung 4.8 ist
diese für zwei unterschiedliche Zeitschritte dargestellt.
Abbildung 4.8: Topologie zweier Oberflächennetze zu unterschiedlichen Zeitpunkten [17]
Das Oberflächengitter wird anschließend in dem Format VRML 1.0 gesichert und in Pointwise als “Grid” eingelesen. Die Klappen- und die Ventrikeloberfläche wurden vom Helmholtz Institut einzeln vernetzt und sind somit in dem VRML Format auch separiert. Somit
werden alle drei Oberflächen in Pointwise als Database erkannt und können zu einem Block
zusammengefasst werden.
Das VRML (Virtual Reality Modeling Language) Format wurde gewählt, da es sich um
ein als Klartext lesbares (ASCII - American Standard Code for Information Interchange)
und ein einfach strukturiertes Datenformat handelt. Es besitzt die Endung .wrl und ist im
Anhang A.1.1 dargestellt.
Um zu überprüfen, ob die Gittertopologie die gleiche bleibt, werden auf dem Oberflächengitter der Mitralklappe, der Aortaklappe und des Ventrikels per Zufall Punkte ausgewählt
und miteinander verglichen. Die zu vergleichenden Punkte werden dabei so gewählt, dass
sie örtlich zusammehängend in einer Reihe liegen. In der Abbildung 4.9 kann erkannt
werden, dass die Knotennummerierung in beiden Abbildungen, bezüglich Position und
Reihenfolge die gleiche geblieben ist.
4.3. Gittergenerierung
(a) 1. Zeitschritt
32
(b) 2. Zeitschritt
Abbildung 4.9: Vergleich der Gitterpunkte für zwei unterschiedliche Zeitschritte am Beispiel des linken Ventrikels
Außerdem kann durch das eigens entwickelte Programm “largestShift” [49] überprüft werden wie groß die Verschiebung zwischen zwei Oberflächennetzen ist. Das Programm benötigt dazu die mxyz.space Datei der beiden Netze und eine der beiden minf Dateien
(sind bei beiden Gittern identisch). Dadurch kann direkt eine Aussage getroffen werden,
ob die beiden Oberflächengitter gleich nummeriert sind. Liegt der Wert unterhalb von
10 mm, kann davon ausgegangen werden, dass eine einheitliche Nummerierung vorliegt.
Werte zwischen 10 und 15 mm können, müssen aber nicht durch eine unterschiedlichen
Nummerierung begründet sein. Alle Werte oberhalb von 15 mm sind jedoch ein eindeutiges Zeichen für eine unterschiedliche Nummerierung und inkompatible Topologie für zwei
Herzgeometrien.
Der zweite Schritt der Vernetzung besteht in der Erzeugung des Volumennetzes. Dieses
wird unter Verwendung des Gittergenerierungsprogramms Pointwise Version 16.0.2.3 erstellt.
4.3.1 Elastic Mesh Update Method
Bei der Erstellung der Volumennetze wird nur das Netz des ersten Zeitschritts mittels des
Programms Pointwise erstellt. Die anschließenden Volumennetze werden mittels Verschiebungsvektoren in dem Strömungslöser XNS gebildet. Die Vektoren für die Oberflächennetze werden mittels eines eigens am CATS Institut entwickelten Programms erzeugt [49].
Das Programm und seine Anwendungsweise wird in den folgenden Absätzen beschrieben.
4.3. Gittergenerierung
33
Zunächst müssen dafür die Oberflächennetze von dem Format VRML 1.0 mit einem am
Institut entwickelten Konverter [49] in das für die Simulation verwendete MIXD-Format
umgewandelt werden. Dies erfolgt mit dem Befehl:
./vrml2mxyz -g -tri <Oberflächennetz - Datei>
Bei der Umwandlung in das MIXD Format, muss vorher das VRML Format des Gitters
überprüft werden. Das Programm “vrml2mxyz” benutzt bei der Konvertierung in das
MIXD Format als Codewort “point[” um mit dem Einlesen der Koordinaten zu beginnen.
Es kann aber vorkommen, dass der hier dargestellte Text:
Separator {
Separator {
Material {
ambientColor 0.000 0.250 0.000
diffuseColor 0.000 1.000 0.000
specularColor 0.500 0.500 0.500
transparency 0.000
shininess 0.600
} Coordinate3 {
point [
statt nur einmal, zweimal oder mehrmals hintereinander geschrieben ist. Wenn dies der
Fall ist, müssen die Wiederholungen gelöscht werden, damit es nicht zu einer fehlerhaften
Konvertierung kommt. Dies wurde manuell vorgenommen.
Anschließend kann der Gesamtverschiebungsvektor zwischen je zwei aufeinanderfolgenden
Oberflächengittern berechnet werden. Dabei werden die einzelnen Differenzvektoren zwischen dem aktuellen und dem darauf folgenden Oberflächennetz errechnet, und die daraus
resultierende Verschiebung bestimmt. Die neuen Koordinaten aller Knoten im Volumennetz werden unter Zuhilfenahme des jeweils vorherigen Volumengitters und des Gesamtverschiebungsvektors mittels des Strömungslösers XNS berechnet.
Der Verschiebungsvektor wird mit dem Programm “shiftVector” erstellt [49]. Zur Ausführung des Programms wird folgender Input File benötigt:
1
2
3
4
5
6
7
!this is input file for shiftVector application
!use "!for comments
!use single space trimming
!
!*****uns***** set to .true. if volume coordinates are saved in *.uns
uns .false.
!*****debug*** set to .true. if more information required
4.3. Gittergenerierung
8
9
10
11
12
13
14
15
16
17
18
19
20
34
debug .true.
!*****mxyz**** name of the file with volume coordinates
mxyz mxyz
!*****s1****** name of the file with the initial surface coordinates
s1 mxyz.space.1
!*****s2****** name of the file with the modified surface coordinates
s2 mxyz.space.2
!*****nn****** number of volume nodes (space only!)
nn 75104
!*****nns***** number of surface nodes (space only!)
nns 13526
!*****delta*** maximal allowed deviation
delta 0.002
Bei dem ersten Gitter, welches mit der Software Pontwise erstellt wird und somit im “.uns”
Format vorliegt, muss in der 6. Zeile des Input Files statt des “false” ein “true” stehen.
Anschließend wird durch Zeile 10 das Volumennetz eingelesen, wenn dieses statt im “.uns”
Format im “mxyz” Format vorliegt, Zeile 12 und 14 lesen die Oberflächennetze ein. In
Zeile 16 muss die Anzahl Gesamtanzahl der Knoten angegeben werden (nur space), in
Zeile 18 die Anzahl der Oberflächenknoten (nur space). Abschließend, in Zeile 20, wird
das Delta definiert. Dieses wird bei der Suche der Koordinaten des Oberflächennetzes im
Volumennetz benötigt und gibt die erlaubte Abweichung an.
Bei der Erstellung des ersten Verschiebungsvektor werden folgende Dateien ausgegeben:
mshift
mshift.space
mshift.pos
Für die Rechnung wird die “mshift” Datei benötigt. Die “mshift.pos” Datei enthält die
Positionen der Oberflächenknoten im Volumennetz, so dass mit dieser Datei, alle Verschiebungsvektoren auch ohne Kenntnis des Volumennetzes erstellt werden können.
Im XNS Input kann durch die Angabe # smallshift <Zahl> $ der Verschiebungsvektor
in beliebig viele gleichmäßige Teile unterteilt werden. Die Zahl gibt dabei an, wie groß eine
Verschiebung anteilmäßig sein soll (0.1 entspricht einem Zehntel der Gesamtverschiebung).
Es kann also eine gewünschte Anzahl an Netzen zwischen zwei Messaufnahmen erstellt
werden und somit die Genauigkeit, bzw. der Aufwand der Rechnung variiert werden. Vor
allem aber gewinnt das von XNS erzeugte Volumenmesh mit kleinerem Verschiebungsvektor deutlich an Qualität und es kommt seltener zum “Tangling” (Abschnitt 3.3).
4.3. Gittergenerierung
35
Um in XNS mit dem Verschiebungsvektor rechnen zu können, sind die in Tabelle 4.1
dargestellten Eingaben im XNS Input nötigt.
Tabelle 4.1: XNS Input für den Verschiebungsvektor
XNS Input
mshift mshift
smallshift <Zahl>
moving on
surface_movement shift
rngxset 11 1 1 1
Erläuterungen
Gibt den Namen der Datei an, welche die Informationen
bezüglich des Verschiebungsvektors beinhaltet
Gibt an, um welchen Anteil des Verschiebungsvektors verschoben werden soll
Ermöglicht die Bewegung des Netzes
Keyword um in XNS das Programm aufzurufen
Gibt an welche RNGs sich bewegen dürfen und welche Richtungen erlaubt sind (bei den Oberflächenknoten sind alle
Bewegungsrichtungen vorgeschrieben)
Die Vorgehensweise um mit EMUM rechnen zu können ist also:
1. Umwandlung des VRML 1.0 Format in das MIXD Format mittels des Befehls
./vrml2mxyz -g -tri <Oberflächennetz - Datei>
2. Verschiebungsvektor mittels des Programm shiftVector und der Input Datei shiftVector.in erzeugen
3. XNS Input anpassen
Abbildung 4.10: Zwei aufeinander folgende Geometrien
Um sich ein Bild von der Verschiebung machen zu können, sind in der Abbildung 4.10
zwei hintereinander folgende Geometrien der 30 MRT Aufnahmen dargestellt.
4.3. Gittergenerierung
36
In der Tabelle 4.2 sind jeweils die maximalen Verschiebungen zwischen zwei aufeinander folgenden Gittern dargestellt. Mit der maximalen Verschiebung ist dabei der Vektor
zwischen zwei Knoten gemeint. Die größte Verschiebung zwischen zwei Knoten in zwei
aufeinander folgenden Geometrien beträgt ca. 13,72 mm, die kleinste 1,88 mm.
Tabelle 4.2: Maximale Verschiebungsvektoren zwischen zwei aufeinander folgenden Netzen
Schritt
max. Verschiebung
Schritt
max. Verschiebung
Schritt
max. Verschiebung
1-2
4,548
11-12
8,769
21-22
2,820
2-3
8,473
12-13
7,736
22-23
2,365
3-4
4,663
13-14
4,260
23-24
2,283
4-5
13,772
14-15
4,039
24-25
1,880
5-6
8,249
15-16
4,178
25-26
3.376
6-7
5,86
16-17
2,229
26-27
2,452
7-8
4,077
17-18
2,931
27-28
3,492
8-9
7,246
18-19
2,803
28-29
2,130
9-10
4,773
19-20
2,657
29-30
2,581
10-11
9,568
20-21
2,656
30 -1
9,194
4.3.2 Anfängliche Probleme bei der Gittererstellung
Die ersten vom Helmholtz Institut gestellten Oberflächennetze enthielten sich überlappende Dreiecke (Abb. 4.11). Diese verhindern eine direkte Generierung des Volumengitters
und erfordern somit eine Überarbeitung des Oberflächengitters, wodurch eine einheitliche
Knotennummerierung nicht mehr garantiert werden kann.
Ein nächstes vom Helmholtz Institut gestelltes und verbessertes Oberfächengitter lässt
sich zwar ohne Probleme vernetzen, bei der Erstellung des Volumengitters des darauf
folgenden Zeitschritts bricht das Programm aber, aufgrund von Tangling, nach ca. einem
4.3. Gittergenerierung
37
Abbildung 4.11: Darstellung der sich überlappenden Dreiecke auf dem Oberflächengitter
Fünftel der Verschiebung ab. Auch nachdem das Gitter stark vergröbert wurde, um so den
Verschiebungsvektor klein gegenüber der Größe der Elemente zu gestalten, kann nur ein
Drittel der Verschiebung erreicht werden.
Um herauszufinden, weshalb die Verschiebung nicht erreicht werden kann, wurde der Skewness Equiangle (Abbildung 4.12) betrachtet. Die Wahl fiel auf dieses Kriterium, da es eine
Aussage über die Güte der Elemente gibt. Der Skewness Equiangle ist definiert als [36]:
max
%
(Qmax − Qe ) (Qe − Qmin )
,
(180 − Qe )
Qe
&
(4.1)
mit
Qmax =größter Winkel in der Zelle (in Grad angegeben)
Qmin =kleinster Winkel in der Zelle (in Grad angegeben)
Qe = Winkel für das gleichseitige Element (70, 53◦ )
Der Wert vergleicht die maximalen Winkel in dem Tetraeder mit denen eines gleichseitigen
Tetraedes und variiert zwischen 0 (gut) und 1 (schlecht). Bis zu einem Wert von 0,8
besitzen die Elemente eine gute Qualität und bis 0,9 sind sie, je nach Strömungslöser,
akzeptabel [36]. Der Wert ist vor allem bei den Elementen schlecht, die sehr große Winkel
aufweisen und somit sehr flach, bzw. spitz sind.
Bei der Betrachtung des Elementes, welches für den Abbruch der Rechnung verantwortlich
ist, stellte sich heraus, dass der Skewness Equiangle schon zu Beginn der Rechnung sehr
hoch ist. Somit kommt es bei der Erstellung des Volumennetzes durch XNS mittels der
EMUM (siehe Abschnitt 3.3) zu einem Tangling des Netzes.
4.3. Gittergenerierung
38
(a) Ursprüngliches Gitter: Werte im Bereich 0.032 (b) Überarbeitetes Gitter: Werte im Bereich 0.015
bis 0.825
bis 0.754
Abbildung 4.12: Skweness Equiangle
In der Abbildung 4.12 sind zwei verschiedene Gitter dargestellt. Abbildung a) zeigt das
ursprüngliche Netz, bei dem es nach einem Drittel der Verschiebung zu einem Abbruch
der Rechnung kommt. Bei diesem liegen die Werte des Skewness Angle zwischen 0.0317
und 0.825. Die roten Elemente zeigen einen besonders hohen Skweness Angle auf. Es lässt
sich deutlich erkennen, dass diese Elemente besonders flach sind und einen spitzen Winkel
aufweisen. Abbildung b) zeigt das überarbeitete Netz, dessen Werte nur noch in einem
Bereich von 0.015 und 0.754 liegen. Zusätzlich hat auch die Anzahl der Elemente mit
einem hohen Skewness Angle abgenommen. Mit diesem Gitter kann schließlich, mit einem
hinreichend klein gewählten Verschiebungsvektor, die erforderliche Verschiebung erreicht
werden.
Zusammenfassend kann gesagt werden, dass die Güte der Oberflächennetze für die Güte
der im Volumengitter gebildeten Tetraeder verantwortlich ist.
Bei den letzen Gittern, bei welchen die Geometrie vorher geglättet wurde, kommt es schon
bei der zweiten Verschiebung zu einem Tangling. Bei Betrachtung der Gitter zeigt sich,
dass das Problem darin liegt, dass bei der Erstellung des Volumennetzes, die Tetraeder
zwischen Ventrikel und der Klappe, über die Ecke erstellt wurden, so dass alle 4 Knoten
einiger Tetraeder auf der Oberfläche liegen (siehe Abb. 4.13 a)). Da der Winkel der Ecke im
Laufe der Verformung aber immer größer wird, müssen sich die Tetraeder mit verformen
und es kommt schließlich, aufgrund schlechter Elementenqualität, zu einem Abbruch der
Rechnung. Der Abbruch der Rechnung ist also nur auf die Elemente auf der Oberfläche
zurück zuführen und hat nichts mit der EMUM zu tun. In der Abbildung 4.13 b) ist der
verformte Tetraeder dargestellt.
4.3. Gittergenerierung
(a) Element zu Beginn der Rechnung
39
(b) Verformtes Element
Abbildung 4.13: Darstellung der sich verformenden Elemente
Nach Betrachtung aller Geometrien, wurde somit Geometrie 7 als Startgeometrie gewählt
(Abbildung 4.14). Bei dieser ist der Übergang zwischen Klappen und Ventrikel besonders
flach, so dass die Tetraeder nicht über der Kante gebildet werden und somit im Laufe der
Verschiebung keine zu große Verformung erfahren.
Abbildung 4.14: 7. Geometrie der extrahierten Gitter
4.3.3 Endgültiges Gitter
Das endgültig verwendete Gitter besitzt die in Tabelle 4.3 festgehaltene Anzahl an Knoten
und Elementen.
Die Verteilung der Elemente ist in der Abbildung 4.15 aufgezeigt, Bild a) zeigt das Gitter mit der Schnittebene, Bild b) die Schnittebene ohne das Gitter. Das Gitter wurde
4.3. Gittergenerierung
40
Tabelle 4.3: Anzahl der Elemente und Knoten (nur space Anzahl)
Elemente
412 695
Gesamtknoten
75 208
Oberflächenknoten
13 526
dabei so gewählt, dass der Skewness Equiangle besonders gut ist. Dieser beträgt bei der
Startgeometrie maximal 0,7989.
(a) Gitter mit Schnittebene
(b) Schnittebene
Abbildung 4.15: Darstellung des Gitters im Schnitt
Auf den folgenden zwei Seiten sind sämtliche 30 Geometrien des linken Ventrikels dargestellt. Bei der Betrachtung der Geometrien und den zughörigen Verschiebungsvektoren
(Tabelle 4.2) wird deutlich, dass zwischen den Schritten 16 und 30 kaum Veränderungen
auszumachen sind und die größten Verschiebungen in der ersten Hälfte stattfinden.
4.3. Gittergenerierung
41
Geometrie 1
Geometrie 2
Geometrie 3
Geometrie 4
Geometrie 5
Geometrie 6
Geometrie 7
Geometrie 8
Geometrie 9
Geometrie 10
Geometrie 11
Geometrie 12
Geometrie 13
Geometrie 14
Geometrie 15
Abbildung 4.16: Geometrien 1 bis 15
4.3. Gittergenerierung
42
Geometrie 16
Geometrie 17
Geometrie 18
Geometrie 19
Geometrie 20
Geometrie 21
Geometrie 22
Geometrie 23
Geometrie 24
Geometrie 25
Geometrie 26
Geometrie 27
Geometrie 28
Geometrie 29
Geometrie 30
Abbildung 4.16: Geometrien 16 bis 30
4.4. Strömungsberechnung
43
4.4 Strömungsberechnung
Bevor mit der Strömungssimulation begonnen werden kann, müssen die Randbedingungen festgelegt werden. Dazu wird zunächst, wie in der Abbildung 4.17 dargestellt, das
Volumen, aufgetragen über die gesamten Zeitschritte der 30 Geometrien, betrachtet. Bei
der Simulation wird der Verschiebungsvektor durch 100 geteilt, sodass nicht nur 30, sondern 3000 Geometrien für die Simulation eines Zyklus verwendet werden. Dies hat zwei
Gründen, zunächst führt ein sprunghaftes Verhalten, welches sich bei nur 30 Geometrien
ergeben würde, bei der Auswertung der Strömung zu keinen guten Ergebnissen, zweitens,
verbessert sich, wie schon vorher erwähnt, die Qualität der Volumengitter bei kleineren
Verschiebungen.
Durch die rote Linie wird der Verlauf der extrahierten Geometrien gekennzeichnet. Das
∆ t zwischen den Zeitschritten beträgt 0,00033 Sekunden. Dieser Wert ergibt sich aus folgender Betrachtung. Die vier Aktionsphasen des Herzens, also Anspannung, Austreibung,
Entspannung und Füllung, verlaufen in ca. einer Sekunde. Wird dieser Wert durch die
30 Aufnahme die während des Zyklus entstanden sind geteilt, ergibt sich eine Zeit von
einer 1/30 Sekunde pro Geometrie. Da die Berechnung von einer Geometrie zur nächsten,
aber nicht in einem sondern in 100 Schritten erfolgt, beträgt die Zeitspanne zwischen zwei
Schritten nur 0,00033 Sekunden.
Abbildung 4.17
Wird der Volumenverlauf der Rechnung mit einer realen Kurve verglichen, wie sie in
Abbildung 4.18 dargestellt ist, zeigt sich, dass der Bereich von 2-15 qualitativ eine gute
4.4. Strömungsberechnung
44
Übereinstimmung aufweist. In der zweiten Hälfte jedoch, weist die Kurve, statt eines
langsamen, stetigen Anstieges, ein sprunghaftes Verhalten auf.
Abbildung 4.18: Herzzyklus
Da dieses Verhalten physiologisch nicht sinnvoll ist, wird eine Glättung der Bewegung des
Ventrikels vorgenommen. Diese geglättete Bewegung wird durch die blaue Linie in dem
Diagramm 4.17 gekennzeichnet.
Begonnen wird bei der Entspannung des Ventrikels. Diese beginnt bei der Geometrie 9. In
der Entspannungsphase verhält sich das Volumen isovolumetrisch, das heißt, dass in dieser
Phase das Volumen sich nicht verändert und beide Klappen geschlossen sind. Um dieses
isochore Verhalten nachzubilden, wird mit dieser gleichbleibenden Geometrie 100 Zeitschritte lang gerechnet. Anschließend wird von dieser Geometrie der Verschiebungsvektor
zu Geometrie 11 gebildet, so dass Geometrie 10 nicht mehr verwendet wird. Mit dem Ende
4.4. Strömungsberechnung
45
des isovolumetrischen Verhaltens beginnt die Füllungsphase und die Mitralklappe öffnet
sich.
Bis Geometrie 14 werden alle extrahierten Geometrien verwendet und jeweils 100 Zeitschritte dazwischen berechnet. Darauf folgend beginnt der unstetige Bereich. Um den
langsamen, stetigen Anstieg zu erhalten, wird zunächst von Geometrie 14 zu Geometrie
19 der Verschiebungsvektor gebildet. Die Dauer der Rechnung entspricht der Zeit, die
auch vorher für den Verlauf von 14 nach 19 benötigt wurde. Hiernach wird der Verschiebungsvektor von Geometrie 19 nach 28 gebildet und die Rechnung in dem entsprechenden
Zeitrahmen durchgeführt. Bei Geometrie 28 angekommen, endet die Füllungsphase, und
die Anspannungsphase, in der wieder beide Klappen geschlossen sind, beginnt. Diese weist
wieder ein isovolumetrisches Verhalten auf, so dass Geometrie 28 für einen Zeitraum von
200 Zeitschritten beibehalten wird. Mit Abschluss der Anspannungsphase beginnt die Füllung und die Aortenklappe öffnet sich.
Der Verschiebungsvektor zwischen Geometrie 28 und 2 wird gebildet, so dass Geometrie 1
nicht mehr verwendet wird. Bis zum Beginn der Entspannungsphase werden alle vorhandenen extrahierten Geometrien verwendet.
4.4.1 XNS Input
Bei der Erstellung der XNS Input Datei muss darauf geachtet werden, dass die Einheiten übereinstimmen. Der Strömungslöser XNS arbeitet mit kinematischen Werten, d.h.
dass alle Werte mittels der Dichte normiert werden. Die Dichte von Blut beträgt ca.
1,058 kg/mm3 . Für die dynamische Viskosität von Blut wurde ein Wert von 3,6 mPas
angenommen, dieser Wert gilt für Körpertemperatur. Die kinematische Viskosität beträgt
2
somit 3,4 mm
s .
Der Duck muss von der Einheit mmHg in die für den XNS Input benötigten Einheit s2kg
mm
umgerechnet werden:
1 mmHg =
1
1
N
1
kg
Pa =
=
−3
−3
2
−3
2
7, 5006 · 10
7, 5006 · 10 m
7, 5006 · 10 · 1000 s mm
(4.2)
daraus folgt :
1 mmHg =
1
kg
2
7, 5006 s mm
(4.3)
Da XNS mit kinematischen Größen arbeitet, muss der Wert noch durch die Dichte dividiert
werde, so dass sich insgesamt ein Umrechnungsfaktor von
4.5. Simulationen
1 mmHg
kg
1058 m
3
46
=
1
kg
1
109 mm2
·
=
7, 5006 s2 mm 1058 kg3
7935, 63 s2
(4.4)
m
ergibt.
Für einen Druck von 1 mmHg ergibt sich mit dem Umrechnungsfaktor ein Wert von
2
126 013,94 mm
für den XNS Input.
s2
Bei den Strömungen im Herzen handelt es sich um laminare Strömungen, sodass in die
Simulation ohne Turbulenzmodell durchgeführt werden. Die vollständigen XNS Input Dateien werden bei der Beschreibung der unterschiedlichen Simulationen angegeben.
4.5 Simulationen
Bevor mit der Simulation des Herzzyklus begonnen werden kann, soll zunächst die Strömung bei einer starren Geometrie und geöffneten Klappen simuliert werden. Die Idee dabei
ist, zunächst eine auskonvergierte Lösung zu erhalten, um darauf aufbauend mit der Simulation der Strömung während der Verformungen zu beginnen. Als Randbedingung wird
der Druck, der während der Auswurfphase zwischen Aorta und Ventrikel herrscht angenommen. Dieser kann aus dem Diagramm 2.4 abgelesen werden und wird zunächst auf
2
einen Wert von 6 mmHg gesetzt, welcher umgerechnet für den XNS Input 756 144 mm
s2
ergibt. Da beide Klappen geöffnet sind, wird an der Mitralklappe, also der Klappe, in
die das Fluid hineinfließt, der berechnete Druck angenommen. An der Aortenklappe, also
dort wo die Strömung hinausfließt, wird kein Druck angegeben, so dass dieser dort Null
ist. Somit herrscht eine Druckdifferenz von 6 mmHg zwischen den beiden Klappen und die
Strömung fließt von der Mitralklappe zur Aortenklappe hin.
4.5.1 Rechnung 1 - Instationär
Zunächst wird eine instationäre Rechnung ausgeführt, die wichtigsten Input Parameter
sind nachfolgend aufgeführt. Der vollständige Input File befindet sich im Anhang A.1.2.2.
Wichtigsten XNS Input Parameter für die 1. Rechnung
dt 0.0003
# Solve parameters
ninner 100
nouter 5
nit 5
4.5. Simulationen
47
# Time discretization
nts 150
steady off
space-time on
# Formulation selection
stokes off
# Turbulence model
turbulence_model none
# Material properties
# all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas
material 1 viscosity 3.4
# wall (11)
rngdset 11 1 1 1
# inflow (12)
rngdflux 12 756144 756144 756144
# outflow (13) (Es werden keine Vorgaben gemacht)
Die instationäre Rechnung divergiert jedoch und bricht nach 98 Schritten ab, wie auch in
der Abbildung 4.19 des Residuen Files zu erkennen ist.
In den Abbildungen 4.20, in der die beiden Klappenebenen dargestellt sind, wird die
Strömung der Rechnung ausgewertet. Die rund geformte Öffnung ist die Aortenklappe, also
die Klappe aus der die Strömung hinausfließt, die andere ist Klappe somit die Mitralklappe,
in die die Strömung hineinfließt.
Nach 10 Zeitschritten, also in dem Bereich, in dem die Rechnung noch nicht divergiert
ist, stimmt zumindest noch die Größenordnung der Geschwindigkeit (ungefähr 1m/s).
Sobald die Rechnung anfängt zu divergieren nimmt auch die Geschwindigkeit um mehr als
zwei Größenordnungen zu. Zwar wurde ein konstanter Druck an der Mitralklappe (Inflow)
vorgegeben, wie aber an dem Geschwindigkeitsprofil zu erkennen ist, ist dieser so nicht
von XNS berechnet worden.
4.5.2 Rechnung 2 - Stationär
In einer zweiten Rechnung soll die Strömung zunächst stationär berechnet werden. Dazu
2
soll die kinematische Viskosität startend von 34 000 mm
auf 3,4 runter gesetzt werden.
s
4.5. Simulationen
48
Abbildung 4.19: Residuum der instationären Rechnung; Abbruch nach 98 Schritten
(a) nts=10
(b) nts=50
Abbildung 4.20: Instationäre Rechnung, Geschwindigkeiten nach 10 und nach 50 Zeitschritten
Denn je höher die Viskosität ist, desto langsamer fließt die Strömung und kann somit leichter simuliert werden. Jede neue Simulation erfolgt als Wiederneustart der alten Rechnung.
Wichtigsten XNS Input Parameter für die 2. Rechnung
(vollständiger Input File im Anhang A.1.2.3)
dt 0.0003
# Solve parameters
ninner 100
4.5. Simulationen
49
nouter 5
nit 300
# Time discretization
nts 1
steady on
space-time on
# Formulation selection
stokes off
# Turbulence model
turbulence_model none
# Material properties
# all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas
material 1 viscosity 34000 (Wert wird bei jedem Neustart weiter runter gesetzt)
material 1 density 1.0
# wall (11)
rngdset 11 1 1 1
# inflow (12)
rngdflux 12 756144 756144 756144
# outflow (13) (Es werden keine Vorgaben gemacht)
Bis zu einer Viskosität von ca. 500 funktioniert die Vorgehensweise, anschließend konvergieren die Lösungen aber nur noch in einem Bereich von 10−4 . Wird versucht die Viskosität
noch weiter herunter zu setzen, beginnt die Rechnung zu divergieren.
Bei den Auswertungen (Abbildung 4.21) zeigt sich, dass auch bei dieser Rechnung mit
abnehmender Viskosität, sich ein sichelförmiges Geschwindigkeitsprofil bildet.
(a) Viscosity=2000
(b) Viscosity=465
Abbildung 4.21: Stationäre Rechnung - Geschwindigkeiten bei einer Viskosität von 2000
und 465
Strömungssimulation des Herzens
# wall (11)
sich, dass auch bei dieser Rechnung mit
rngdset 11 1 1 1
Simulation
s Geschwindigkeitsprofil bildet.
n ca. 500 funktioniert die Vorgehensweise, anschließend koninflow
(12) Bereich von 10−4 und wird versucht die
r nur #
noch
in einem
4.5. Simulationen
12 756144
756144
756144
er zu rngdflux
setzen, beginnt
die Rechnung
zu divergieren.
-
n (3)
50
# outflow
(13) sich, dass auch bei dieser Rechnung mit
bildung
4.21) zeigt
Wird der Geschwindigkeitsverlauf im Schnitt betrachtet, kann jedoch die Bildung von zwei
g ein sichelförmiges Geschwindigkeitsprofil
ch
bildet.
Bis zu einer Viskosität
von ca.
500 funktioniert
die Vorgehensweise,
anschließend konWirbeln
erkannt
werden (Abbildung
4.22).
−4
die Lösungen aber nur noch in einem Bereich von 10 und wird versucht die
n v n vergieren
der Klappenebene
v im Schnitt
Viskosität noch weiter runter zu setzen, beginntDarstellung
die Rechnungvon
zu divergieren.
Bei den Auswertungen (Abbildung 4.21) zeigt sich, dass auch bei dieser Rechnung mit
abnehmender Viskosität, sich ein sichelförmiges Geschwindigkeitsprofil bildet.
(b) Viscosity=465
=2000
(b) Viscosity=465
Rechnung - Geschwindigkeiten bei einer Viskosität von 2000
ationär
(a) Viscosity=2000
(b) Viscosity=465
Abbildung 4.21: Stationäre Rechnung - Geschwindigkeiten bei einer Viskosität von 2000
und 465
Abbildung 4.22
onären
Rechnung
zu
erhalten.
Außerdem
wird
der
Druck
von
13
windigkeiten bei einer
Viskosität von
2000 Schmitz
Diplomvortrag
- Stephanie
tergesetzt. Die übrigen Eingaben unterscheiden sich nicht von
y=3,4
ird versucht mit Erhöhung der inneren und äußeren Iterationen
4.5.3 Rechnung 3Um
- Instationär
die Strömung weiter zu betrachten, werden weitere Untersuchungen durchgeführt.
Parameter für die 3. Rechnung
In einer dritten Rechnung wird versucht mit Erhöhung der inneren und äußeren Iterationen
eine Konvergenz der instationären Rechnung zu erhalten. Außerdem wird der Druck von
6 mmHg auf 1 mmHg heruntergesetzt. Die übrigen Eingaben unterscheiden sich nicht von
4.5.3 Rechnung 3 - Instationär
denen der ersten Rechnung.
Wichtigsten XNS Input Parameter für die 3. Rechnung
In einer dritten Rechnung wird versucht mit Erhöhung der inneren und äußeren Iterationen
# Solve parameters eine Konvergenz der instationären Rechnung zu erhalten. Außerdem wird der Druck von
ninner 600
6 mmHg auf 1 mmHg heruntergesetzt. Die übrigen Eingaben unterscheiden sich nicht von
denen der ersten Rechnung.
Wichtigsten XNS Input Parameter für die 3. Rechnung
# Solve parameters
ninner 600
nouter 15
nit 5
# inflow (12)
rngdflux 12 126024 126024 126024
Auch hier beginnt die Rechnung nach ca. 30 Zeitschritten langsam zu divergieren und das
Geschwindigkeitsprofil im Inflow weisst immer noch eine sichelförmige Form auf.
4.5. Simulationen
51
4.5.4 Rechnung 4 - Instationär
Um bei der Rechnung sicher zu gehen, dass der Druck konstant in der Ebene der Mitralklappe gesetzt wird und an sämtlichen Wände eine Geschwindigkeit von Null herrscht,
werden die Randbedingungen geändert.
An den Wänden wird die “noslip” Kondition gesetzt, so dass dort die Geschwindigkeit Null
ist. Wird in XNS Input nur ein RNG spezifiziert wird, ist die “noslip” Bedingung nahezu
äquivalent zu der Eingabe rngdset %d 1 1 1. Jedoch bewirkt der “noslip” Befehl, dass die
benachbarten Randbedingungen überschrieben werden, der Befehl “rngdset” verursacht
dies nicht.
Da das Koordinatensystems des Ventrikels nicht mit dem der Mitralklappe übereinstimmt,
wird mit dem Befehl “rngalign” dieses in die Mitralebene gedreht. Anschließend wird mit
dem Kommando “rngdset 12 1 1 0” nur noch die Geschwindigkeitskomponente in Normalenrichtung zur Klappenebene zugelassen. Der Druck wird wie auch in den vorherigen
Rechnung angegeben.
Wichtigsten XNS Input Parameter für die 4. Rechnung
# Solve parameters
ninner 150
nouter 7
nit 6
nts 100
# wall (11)
noslip 11
# inflow (12)
rngalign 12
rngdset 12 1 1 0
rngdflux 12 63012 63012 63012
# outflow (13) (Vorgabe eines Druckes von 0)
rngdflux 13 0 0 0
Aber auch diese Rechnung zeigt nicht den gewünschten Residuenverlauf (Abbildung 4.23).
Das Geschwindigskeitsprofil weist die selbe Form wie die vorherigen Rechnungen auf.
4.5.5 Rechnung 5 - Instationär
Bei der 5. Rechnung werden die Einstellungen wie in der 4. Rechnung vorgenommen, nur
dass diesmal der Druck mittels einer Funktion (siehe XNS Input) langsam erhöht wird.
4.5. Simulationen
52
Abbildung 4.23: Residuum der 4. Rechnung
Wichtigsten XNS Input Parameter für die 5. Rechnung
# inflow (12)
rngalign 12
rngdset 12 1 1 0
rngdflux 12 63012*min(1.0,t/(50*dt)) 63012*min(1.0,t/(50*dt)) 63012*min(1.0,t/(50*dt))
Abbildung 4.24: Residuum der 5. Rechnung
Das Residuum der Rechnung, welches in der Abbildung 4.24 dargestellt ist, ist vom Verlauf
her akzeptabel.
Um zu überprüfen, ob die Randbedingungen auch richtig gesetzt worden sind, wird der im
XNS Input der Befehl “debug bc” eingegeben. Dieser bewirkt die Ausgabe der Datei “da-
4.5. Simulationen
53
ta.bc”, welche Informationen zu den gesetzten Randbedingungen beinhaltet. Diese setzten
sich aus nsd × nsd (Number of space dimension) Freiheitsgraden pro Knoten und dem
Vektorfeld nsd zusammen. Im dreidimensionalen beinhaltet das erste Feld von jedem Knoten entweder einen Einheitsvektor in der Richtung î (nicht ausgerichteter Knoten) oder in
Richtung t̂ (ausgerichteter Knoten), wenn diese von einer Dirichlet Randbedingung festgelegt ist (unabhängig vom Wert) oder den Wert Null, wenn keine Richtung vorgegeben
ist. Das zweite und dritte Feld sind genauso wie das erste Feld aufgebaut. Somit kann
überprüft werden, ob die Geschwindigkeit am Inflow wirklich nur in Normalenrichtung zugelassen wurde. Bei der Auswertung stellt sich heraus, dass die Randbedingungen in XNS
richtig gesetzt worden sind. In der Abbildung 4.25 ist die Auswertung veranschaulicht und
die erlaubten Geschwindigkeitsrichtungen sind mit Hilfe von Pfeilen dargestellt.
Abbildung 4.25: Auswertung des “data.bc” Files, erstellt von M. Behr
Das Geschwindigkeitsprofil, welches in der Abbildung 4.26 zu erkennen ist, hat sich noch
immer grundlegend geändert.
Abbildung 4.26: Geschwindigkeitsprofil in der Klappenebene
4.5. Simulationen
54
Ein Problem bei der Strömungsberechnung könnte sein, dass zwischen den beiden Klappen der Winkel sehr flach ist. Das Fluid muss somit, von der am Inflow nur zulässigen
Geschwindigkeit normal zur Klappenebene, sich um 90◦ C drehen um dann parallel an der
Wand zwischen Mitral- und Aortenklappe entlang zu fließen (siehe dazu auch Abbildung
4.25). So dass in der Realität wohl keine parallele Strömung am Inflow herrscht und andere
Randbedingungen gefunden werden müssen.
An dieser Stelle endet der erste Teil der Arbeit. Im nächsten Kapitel erfolgt die Simulation
des Thrombozytenwachstums in einer Koronararterie.
55
5 Simulation des Thrombozytenwachstums
in einer Koronararterie
Ziel dieser Simulation ist es, eine Methodik zur Berechnung der benötigten Reaktionsraten für einen nahezu vollständigen Verschluss einer Koronararterie zu ermitteln. Die
zeitlich zunehmende Gefäßverengung soll mittels der in XNS implementierten AdvektionsDiffusions-Reaktions-Gleichungen und unter dem Einfluss von hohen Scherraten bestimmt
werden. Der Aktivierungsgrad der die Stenose durchströmenden Thrombozyten ist scherratenabhängig und wird aufgrund nicht vorhandener Messdaten abgeschätzt. Die benötigten
Verschlusszeiten sollen im Anschluss dabei so ermittelt werden, dass die gleichen Zeiten,
wie auch in dem Experiment von Ku und Flannery [26], erhalten werden. Als Resultat der
Simulation ergibt sich eine Abhängigkeit der Reaktionsraten von der Scherrate.
5.1 Stand der Forschung
Das Verhalten der Thrombozyten unter hohen Scherraten wurde schon in Kapitel 2.4.1
beschrieben, aus diesem Grund soll hierauf verwiesen werden.
5.2 Arbeitsschritte
Die Simulation erfolgt in mehreren Schritten. Zunächst wird ein einfaches Rohr vernetzt
und mit Hilfe eines Verschiebungsvektors und der Elastic Mesh Up Methode in die Form eines Gefäßes mit stenotischer Verengung gebracht. Die Geometrie wird anschließend weiter
verformt, bis ein nahezu vollständiger Verschluss vorliegt. Der Verschiebungsvektor wird
dabei klein gehalten und es erfolgt eine Ausgabe sämtlicher Geometrien, so dass diese bis
zu dem annähernd vollständigen Verschluss vorliegen.
Von der Geometrie einer gegebenen Anfangsstenose (Abbildung 5.3) ausgehend wird die Simulation des Thrombenwachstums gestartet. Zunächst wird eine Strömungsberechnung in
XNS durchgeführt, damit eine auskonvergierte Lösung vorliegt. Auf dieser Rechnung aufbauend werden die Advektions-Diffusions-Reaktionsgleichungen in XNS gelöst. Anschlie-
5.3. Aufbau des Experiments
56
!"#$"%&'(")*+,,-.,/&&"0$&,1/#,0/2",&.,2"&"!0'3",&4",#5!6/%",2"3#'&*,.6,%.))/7"3,6'8!')#+,,
ßend werden die
Reaktionsraten ermittelt, so dass die numerischen Ergebnisse mit den
experimentellen96&"!,%.))/7"3,%./&'37:,&4",&"#&,#"%&'.3#,1"!",$"!65#"2,1'&4,;<=,0>,.6,?@A,/32,)/'2,6)/&,
Daten von Ku und Flannery [26] übereinstimmen. Die Geometrie der
folgenden Stenose
wird dabei dem erfolgten Thrombozytenbewuchs angepasst.
53&'),5#"2,'3,"B$"!'0"3&/&'.3+,,
,
!"#$%&'()*+%
5.3 Aufbau, desC.!,"/%4,"B$"!'0"3&:,D=E,0>,.6,&4",1.!F'37,6)5'2,1/#,&!/3#6"!!"2,'3&.,/,GEE,0>,
Experiments
$)/&")"&,&!/3#6"!,8/7,H@/B&"!<C"31/):,I""!6'")2:,J>K+,,C.!,&4",6'!#&,"B$"!'0"3&,.6,"/%4,3"1,
Da bei dieser Arbeit auf das Experiment von Ku und Flannery [26] zurückgegriffen wird,
8/7:,&*$'%/))*,/,3.3<#&"3.&'%,%.3&!.):,/3,/22'&'.3/),;E,0>,.6,6)5'2,1/#,/22"2,&.,6')),&4",
soll dieses hier kurz erläutert werden. In der Abbildung 5.1 ist der schematische Aufbau
/22'&'.3/),&58'37+,,J6,6)5'2,!"0/'3"2,'3,&4",!"#"!(.'!,/6&"!,.3","B$"!'0"3&,&4"3,&4",
dargestellt. Das Blutreservoir des Systems befindet sich 30 cm über der Testsektion und
endet in einem !"L5'!"2,/0.53&,1/#,/22"2,&.,!"&5!3,'&,&.,D=E,0>+,,M4",$)/&")"&,&!/3#6"!,8/7,1/#,/&&/%4"2,
mit Kollagen beschichteten Zylinder. Für jedes Experiment werden 240 ml
Blut in einen für&.,NG,%0,.6,O,00,'33"!,2'/0"&"!,HJIK,('3*),&58'37,14'%4,%.33"%&"2,&.,/,&4!"",1/*,(/)(",
500 ml vorgesehenen “Capacity Platelet Transfer Bag” transferiert. Dieses
ist über ein Vinylrohr,
welches eine Länge von 85 cm und einen Innendurchmesser von 3
1'&4,&4",&"#&,#"%&'.3,/32,&4",$!"##5!",&!/3#25%"!+,,C'75!",P,8").1,#4.1#,/,#%4"0/&'%,.6,
mm besitzt, mittels eines Dreiwegeventils mit der Testsektion und dem Druckaufnehmer
&4",6).1,#*#&"0+,
verbunden.
,
, ?)/&")"&,M!/3#6"!,@/7,
,
,
?!"##5!",M!/3#25%"!,
OE, %0
M"#& A"%&'.3
,
,
,
,
!"#$%&'(+,,C).1,A*#&"0,J))5#&!/&'.3+,
Abbildung 5.1: Aufbau des Experiments [13]
,
DN,
,
Die Reynoldszahl im oberen Strom liegt zwischen 20 und 120. Das System ist so aufgebaut,
dass keine Rezirkulation des Blutes erfolgt. Als Blut wird Schweineblut verwendet, welches
mit Heparin versetzt wurde. Das Experiment wird bei Raumtemperatur durchgeführt (in
der Arbeit von Bark [4] wird diese mit 27◦ C angegeben ). Während des Experiments werden
Videoaufnahmen erstellt und somit der Thrombenwachstum über der Zeit ermittelt.
Bei den hohen Scherraten, die im Experiment von Ku und Flannery [26] herrschen, kommt
es kaum zur Ausbildung eines Fibrinnetzes. Insbesondere bildet sich ein weißer Thrombus
aus, welcher auch in der Abbildung 5.2 dargestellt ist. So kann der Einfluss der plasmatischen Gerinnungskaskade in diesem Fall vernachlässigt werden und das ADR-Modell,
welches die Gerinnungskaskade nicht abbildet, kann verwendet werden.
5.4. Gittergenerierung - Elastic Mesh Update Method
57
Abbildung 5.2: Experimentelle Ergebnisse des Thrombozytenwachstums, nach einer Zeit
von 0:06, 8:06 und 13:21 Minuten nach Begin der Strömung [4]
5.4 Gittergenerierung - Elastic Mesh Update Method
Zunächst wird ein Rohr mit einem Durchmesser von 1.5 mm und einer Länge von 34 mm
mittels eines unstrukturierten Gitters vernetzt.
Um die Geometrie für die Stenose zu erhalten wird die Gleichung 5.1 nach Young und
Tsai [57] verwendet. Diese definieren die achsensymmetrische Stenose mittels einer Kosinuskurve.
S(x) =

*
+2
 S0 R0 1 − cos( 2π(x−x0 ) )
4
L
0
x0 ≤ x ≤ (x0 − L),
anderenfalls
(5.1)
Dabei stellt S(x) die Randgeometrie der Stenose dar, S0 den Bruchteil des Radius auf den
sich die Stenose verengen soll, R0 =0.75 mm ist der Radius der Region, in der keine Stenose
vorliegt, und x0 definiert den Beginn der Stenose. Mit L ist die Länge definiert über die
sich die Stenose ausbreitet. In der Arbeit von Bark [4] wurde mit Hilfe von Versuchen
für L ein Wert von 4 mm ermittelt. In der Abbildung 5.3 ist die Geometrie der Stenose
dargestellt, von welcher die Thrombosesimulation gestartet werden soll.
Um die Geometrie (Abbildung 5.3) der Stenose zu erhalten, die durch die Gleichung 5.1
definiert ist, wird die EMUM (siehe Kapitel 3.3) verwendet. Dazu wird mittels eines am
Institut geschriebenen Programms “moveCoordinates” [49] und der darin implementierten
Gleichung 5.1 ein Verschiebungsvektor erstellt. Dieser sorgt dafür, dass das anfängliche
5.4. Gittergenerierung - Elastic Mesh Update Method
"#$$
%'&#$$
%&'"#$$
58
%"',#$$
()*+
!"#$$
Abbildung 5.3: Geometrie der Stenose
Gitter der Rohrströmung in die gewünschte Geometrie verformt wird. Um das Programm
zu starten wird folgende Eingabe benötigt:
./moveCoordinates -g mxyz.space
Zunächst fragt das Programm die Anzahl der Volumenknoten ab (nn_space) und erstellt
den Verschiebungsvektor. Anschließend wird nach der Eingabe eines Deltas verlangt. Diese
wird benötigt, um in dem Bereich der zu verschiebenden Knoten, die Oberflächenknoten
zu ermitteln. Denn durch die Vergitterung des Rohres, kann kein perfekter Kreis mehr
erhalten werden und somit ist das Delta definiert durch den Radius des ursprüngliches
Kreises subtrahiert von dem der Oberflächenkoten.
Dieser Verschiebungsvektor wird auch verwendet um die Arterie weiter zu verengen. In der
Abbildung 5.4, sind zwei verschiedene Geometrien der Stenose dargestellt. Abbildung a)
zeigt eine Zwischengeometrie (90,87 % Stenose) zwischen Startgeometrie und Verschluss,
Abbildung b) zeigt die Geometrie des nahezu vollständigen Verschlusses (99,98% Stenose)
der Arterie.
(a) Zwischengeometrie;
90,87% Stenose
(b) nahezu vollständiger Verschluss; 99,98%Stenose
Abbildung 5.4: Darstellung unterschiedlicher Geometrien der Stenose
Die Stenose wird dabei definiert als:
%Stenose =
A1 − A2
D2 − D2
· 100% = 1 2 2 · 100%
A1
D1
(5.2)
Dabei stellt A1 die Querschnittsfläche der Arterie und A2 die Querschnittsfläche der Verengung dar. Der Durchmesser der Stenose lässt sich mit folgender Gleichung berechnen:
5.4. Gittergenerierung - Elastic Mesh Update Method
D2 =
,
D12 ·
!
1−
%Stenose
100%
"
=
-
D12 · (1 − 0, 78) = 0.7035mm
59
(5.3)
5.4.1 Anfängliche Probleme bei der Gittererstellung
Zunächst kommt es bei der Rechnung aufgrund eines zu grob gewählten Gitters zu Netzabhängigkeiten. In der Abbildung 5.5 a) (oberes Bild) kann erkannt werden, dass das Geschwindigkeitsprofil nach Durchlaufen der Verengung nicht mehr symmetrisch ist. Wird
der Bereich der Verengung in Abbildung 5.5 b) (oberes Bild) genauer betrachtet, ist das
durch die Verformung sehr schlecht gewordene Netz zu erkennen. Die Elemente im Teil
der Stenose sind besonders lang gezogen und die eigentlich rundgeformte Stenose weist
Kanten auf.
(a) Geschwindigkeitsprofil
(b) Netz des Arterie in der Verengung
Abbildung 5.5: Darstellung der Netzabhängigkeiten und Netzqualität
Obere Bilder: Grobes Netz
Untere Bilder: Lokal verfeinertes Netz
Aus diesem Grund wurde das Gitter vor allem in dem Bereich der Stenose besonders
verfeinert. Die unteren Bilder der Abbildung 5.5 zeigen jeweils das verfeinerte Gitter.
5.4.2 Endgültiges Gitter
Das endgültig verwendete Gitter, welches schon im vorherigen Abschnitt gezeigt worden
ist, stellt ein unstrukturiertes Gitter dar. Im Bereich der Stenose ist es, aufgrund der
zunehmenden Verengung, besonders verfeinert und vergröbert sich zum Ein- und Ausfluss
hin immer mehr. In der Abbildung 5.6 sind die unterschiedlich verfeinerten Gebiete des
Gitters dargestellt. Abbildung a) zeigt den Bereich in der Stenose, Abbildung b) stellt den
Bereich in der Einströmung dar.
Die Anzahl der Knoten und Elemente des Gitters sind der Tabelle 5.1 zu entnehmen.
5.5. Strömungsberechnung
60
Skewness Equiangle
Skewness Equiangle
0,8150
0,8150
0,6569
0,6569
0,4988
0,4988
0,3407
0,3407
0,0183
0,0183
0,0244
0,0244
(a) Skewness Equiangle des Gitters in der Mit- (b) Skweness Equiangle des Gitters in Nähe
te
der Einströmung
Abbildung 5.6: Darstellung des Skewness Equiangle des Gitters in verschiedenen Ebenen
Tabelle 5.1: Anzahl der Elemente und Knoten (space)
Tetraeder
Knoten
927 496
167 118
5.5 Strömungsberechnung
Die Strömungsberechnung wird als instationäre Rechnung durchgeführt, welche zum auskonvergieren gebracht wird. Die genauen Einstellungen der verschiedenen Parameter können im Anhang A.2.2 aus dem XNS Input File entnommen werden.
Bei der Strömungsberechnung wird das Geschwindigkeitsprofil im Einlaufbereich vorgegeben. Die Randbedingungen werden dabei so gewählt, dass die Ergebnisse mit den experimentellen Daten von Ku und Flannery [26] verglichen werden können. Diese führen
verschiedene Versuche mit unterschiedlichen Anfangsstenosen bis hin zum Verschluss der
Arterie durch. In dieser Arbeit soll auf das Experiment mit einer Anfangsstenose von 78%
zurückgegriffen werden.
Für den Volumenstrom ermittelten Ku und Flannery [26] eine lineare Abhängigkeit zur
Stenose:
%Stenose(t) = −0.78 · Q(t) + 100
(5.4)
5.5. Strömungsberechnung
61
Q(t) wird dabei in der Einheit ml/min angegeben. Mit Hilfe dieser Gleichung kann für
jede Stenose der benötigte Volumenstrom berechnet werden. Bei einer Anfangsstenose von
78% ergibt sich somit ein Volumenstrom von Q(t)=28,21 ml/min=470,09 mm3 /s.
Das Strömungsprofil soll dabei als Paraboloidprofil angegeben werden (siehe Abbildung
5.7).
r
d
v(r)
Abbildung 5.7: parabolisches Geschwindigkeitsprofil v(r) bei laminarer Rohrströmung
Das Paraboloidprofil kann mit der Gleichung
v(r) = α · r2 + β · r + γ
(5.5)
beschrieben werden. Aus den Randbedingungen
v(r)r=0 = vmax
und
v(r)r=±R = 0
(5.6)
folgt
v(r) = vmax
.
r2
1− 2
R
/
.
(5.7)
Da für die Eingabe in XNS kartesische Koordinaten benutzt werden, wird der Radius mit
r2 = x2 + y 2
(5.8)
umgeformt. Der Zusammenhang zwischen der maximalen Geschwindigkeit vmax , der mittleren Geschwindigkeit v̄ und dem Einlaufvolumenstrom Q̇ kann mit den folgenden Gleichungen hergestellt werden:
Q̇ =
0
A
vdA
mit
dA = 2πrdr
(5.9)
5.5. Strömungsberechnung
62
Nach Einsetzen, Kürzen und Umformen folgt:
vmax =
2Q̇
πR2
(5.10)
Die mittlere Geschwindigkeit ergibt sich aus
v̄ =
Q̇
Q̇
1
=
= vmax
A
πR2
2
(5.11)
So dass im XNS Input file das Geschwindigkeitsprofil am Einlauf für die Anfangsstenose
folgendermaßen lautet:
# inflow (11)
rngdset 11 1 1 1
rngdexp 11 3 (-1)*519.94*(1-(((x*x)+(y*y))/(0.5625)))
Zusätzlich zu den Strömungsgeschwindigkeiten, wird in XNS bei Verwendung des Befehls
“recover on” die Vergleichsschubspannung τvs im gesamten Strömungsfeld berechnet. τvs
ergibt sich aus der zweiten Invariante II des deviatorischen Schubspannungstensors und
wird definiert durch:
τvs = −II0,5
τ
(5.12)
Weiterhin gilt für die Scherrate:
γ̇ =
τvs
η
(5.13)
Die ortsabhängige Reynoldszahl kann nach der Gleichung:
Re =
ρvD
,
η
(5.14)
mit
ρ = 1035
kg
m3
und η = 3, 8mP as
berechnet werden. Der Wert für die Dichte ist dabei aus der Arbeit von Bark [4] und
die Viskosität von Blut bei einer Temperatur von 27◦ C [4] aus der Arbeit von Ku und
Flannery [26] entnommen.
5.5. Strömungsberechnung
63
In der Abbildung 5.8 ist der Verlauf des Thrombozytenwachstums der experimentellen Ergebnisse von Ku und Flannery [26], bei einer Anfangsstenose von 78% dargestellt. In der
Abbildung sind bis zum Verschluss der Stenose, sieben Messpunkte mit Angabe der Zeit
und der prozentual belegten Fläche dargestellt. In der Tabelle 5.2 sind diese Messpunkte
mit den zugehörigen Angaben festgehalten.
Die Abbildung 5.8 zeigt, dass der Durchmesser in den ersten 12,4 Minuten von 703,56 µm
auf 302.5 µm abnimmt. In dem Zeitraum von ungefähr Minute 12,4 bis 14,13 wird die Anhaftung der Plättchen mehr als verdoppelt, anschließend nimmt diese bis zum Verschluss
bei 16.5 min wieder ab.
*+,-"($./0"+%1"+2340.22%&5)
7
6
"!!
5
*!
)!
(!
4
'!
&!
3
%!
$!
#!
2
"! 1
!
!
#
%
'
)
"!
"#
"%
"'
!"#$%&'#()
Abbildung 5.8: Experimentelle Auswertung des Experiments von Ku und Flannery, bearbeitet nach [26]
Tabelle 5.2: Messpunkte des Experiments von Ku und Flannery [26]
1
Prozentualer
Verschluss [%]
0
Stenose
[%]
78,00
Durchmesser
[µm]
703,56
2
10
82,18
633,24
2,4
3
33,24
90,19
469,7
8,27
4
57,00
95,93
302,5
12,4
5
84,29
99,46
110,5
14,13
6
91,43
99,84
60,3
15,33
7
94,86
99,94
36,2
16,45
Messpunkt
Zeit [min]
0
Von diesen sechs Punkten werden in der numerischen Simulation aber nur die ersten 5
simuliert. Für den sechsten Punkt ist die Verformung des Netzes so groß, dass nicht mehr
5.5. Strömungsberechnung
64
gewährleistet werden kann, dass die Strömung richtig berechnet wird. In der Abbildung
5.9 ist das Netz bei einer Stenose von 99,53% dargestellt. Der Bereich der Stenose weist
schlechte Elementenqualität auf, was dazu führt, dass es in diesem Bereich zu Netzabhängigkeiten kommen kann.
Abbildung 5.9: Netz bei einer Stenose von 99,53 %
In der Tabelle 5.3 sind die verschiedenen Rechnungsgrößen mit ihrer Größe und Einheit
für die unterschiedlichen Stenosen angegeben. Die Stenose kann mit dem Durchmesser bestimmt werden. Dieser lässt sich aus dem prozentualen Verschluss bestimmen. Dazu muss
der Durchmesser der Anfangsstenose von 78% mit dem jeweiligen prozentualen Verschluss
multipliziert werden und anschließend dieser Wert von der Anfangsstenose subtrahiert
werden. Für den 10 % Verschluss, sieht die Gleichung folgendermaßen aus:
DP V =10% = 703, 56 − (703, 56 · 10%) = 633, 24µm
Die Stenosen entsprechen dabei nicht immer genau denen des Experimentes, da bei der
Extrahierung der Geometrien mit den vorliegenden Geometrien gearbeitet werden muss
und somit die nächstliegende verwendet wird. Der Fehler liegt dabei unterhalb von 0,5%.
Bei Betrachtung der Reynoldszahlen wird deutlich, dass die Strömung laminar gerechnet
werden kann.
Zu jeder dieser fünf Geometrien wird die Strömung berechnet bis sie auskonvergiert. In
der Abbildung 5.10 ist als Beispiel das Residuum der Strömungsberechnung für die 78,5%
Stenose dargestellt. Vor allem die Scherraten spielen für die weitere Berechnung eine große
Rolle. Sind alle Strömungen berechnet, kann mit der Simulation des Thrombenwachstums
begonnen werden.
5.6. Vorbereitung zur Berechnung des Thrombenwachstums
65
Tabelle 5.3: Angabe der Rechnungsgrößen zu den unterschiedlichen Stenosen
Stenose
[%]
78,5
Durchmesser
[µm]
696
Volumenstrom
3
Q [ mm
s ]
459,60
81,90
633,04
89,90
vmax [ m
s]
ReArterie
ReStenose
519,94
106,21
234,23
386,60
437,55
89,38
211,79
476,00
216,45
244,97
50,04
157,37
95,9
303,60
87,53
99,07
20,53
100,77
99,3
121
13,90
15,73
3,21
39,84
Abbildung 5.10: Residuum der Strömungsberechnung der 78,5% Stenose
5.6 Vorbereitung zur Berechnung des Thrombenwachstums
Um den Zeitverlauf des Thrombenwachstums simulieren zu können, müssen die in Kapitel
3.1.2 beschriebenen ADR Gleichungen verwendet werden. Damit diese in XNS berechnet
werden, müssen die in Tabelle 5.4 angegebenen Eingaben im XNS Input gemacht werden
(im Anhang A.2.3 befindet sich verschiedene XNS Input File).
5.6. Vorbereitung zur Berechnung des Thrombenwachstums
66
Tabelle 5.4: XNS Input der ADR Gleichungen
XNS Input
advection
daux data.aux
ambient steady
material 1 viscosity Dbi + Ds
material 2 viscosity Dbi + Ds
material 3 viscosity 2.57e
− 044
1
23
Db,ADP
initexp 1 0.0
initexp 2 0.0
initexp 3 0.0
platelet_model adr_1 1234
3.6 0.000
1 23 4
1
23
4
(∗∗) (∗∗∗)
(∗)
# New configuration input for k-value in
XNS-Stock:
#for krs
kexp 13 1 0.7143
1 23 4 ((krs )*heaviside(-15.5(∗)
1 23 4
(∗∗)
z)*heaviside(z+18.5))
#shear-dependent reaction rate as a function of the coordinates:
#for kas
kexp 13 2 0.7143
1 23 4 ((kas )*heaviside(-15.5(∗)
1 23 4
(∗∗)
z)*heaviside(z+18.5))
#for kaa
kexp 13 3 0.7143
1 23 4 ((kaa )*heaviside(-15.51 23 4
(∗)
(∗∗)
z)*heaviside(z+18.5))
# inflow (11)
rngdset 11 1 1 1
rngdexp 11 1 0.45
rngdexp 11 2 0.35
rngdexp 11 3 0.0
Bedeutung
Keyword um die ADR Gleichungen lösen zu
können
Einlesen des vorher berechneten Strömungsprofils
Geschwindigkeitsfeld wird als konstant angenommen
Festlegung der Diffusionskoeffizienten von
1= Resting Platelets, 2=Activated Platelets,
3=ADP
Berechnung siehe Gleichungen 5.15 und 5.16
Anfangskonzentrationen von RP, AP und
ADP im Fluid; hier zu Null gesetzt
(∗) =
ˆ Angabe des Thrombosemodells (zur
Zeit nur ein Modell in XNS implementiert)
(∗∗) =
ˆ Kennzahl der Thrombozytenaktivierung
(∗ ∗ ∗) =
ˆ Kennzahl der Aggregationswahrscheinlichkeit
(*)=Oberflächenkapazität
ˆ
=
= MInf ty = 0, 7143
Berechnung siehe Gleichung 5.18
(**)=
ˆ Faktor für krs
(*)=Oberflächenkapazität
ˆ
=
= MInf ty = 0, 7143
Berechnung siehe Gleichung 5.18
(**)=
ˆ Faktor für kas
(*)=Oberflächenkapazität
ˆ
=
= MInf ty = 0, 7143
Berechnung siehe Gleichung 5.18
(**)=
ˆ Faktor für kaa
Konzentrationen der RP ([RP ]0 ) und AP
([AP ]0 ) am Inflow
5.6. Vorbereitung zur Berechnung des Thrombenwachstums
67
Um die Werte für den XNS Input bestimmen zu können, werden die im folgenden beschriebenen Gleichungen benötigt:
Der Brownsche Diffusionkoeffizient für die Spezies RP und AP berechnet sich nach:
Dbi =
kB T
= 5, 02 · 10−14 mm2 /s
6πηRi
(5.15)
mit
kB = 1, 38 · 10−23 J/K
T = 300K(aus [4]) η = 3, 8mP as hier: Ri = RP LT = 1, 15µm
Die verstärkte Diffusivität wird mit der Gleichung nach Zydney und Colton [58] bestimmt:
2
Ds = 0, 15 · RRBC
· γ̇ · Hct · (1 − Hct)0,8
(5.16)
mit
RRBC = 2, 75µm
Hct = 0.47
Als Hämatokritwert wurde ein Mittelwert aus den Angaben in der Arbeit von Bark [4]
genommen. Für die Scherrate γ̇ wird die Hälfte des Maximalwertes, der sich bei der Strömungsberechnung ergibt, verwendet. Um den Einfluss der Diffusivität zu überprüfen, wurden zwei Rechnungen durchgeführt. Diese unterschieden sich nur darin, dass die Diffusivität einmal mit der maximalen und das andere mal mit der Hälft der maximalen Scherrate
berechnet wurde. Dabei stellte sich heraus, dass die Ergebnisse für das Thrombenwachstum sich um weniger als 0,1% unterschieden.
ADP besitzt einen Brownschen Diffusivitätskoeffizienten von:
Db,ADP = 2, 57 · 10−4 mm2 /s
(5.17)
Die Oberflächenkapazität bestimmt sich aus:
MInf ty =
M∞
= 0, 7143mm
P [P LT ]∝
(5.18)
5.6. Vorbereitung zur Berechnung des Thrombenwachstums
68
P LT
2
mit M∞ = 25 · 104 mm
2 als maximaler Anzahl an kugelförmigen Thrombozyten pro mm
P LT
und einer Anfangskonzentration an Thrombozyten von P [P LT ]∝ = 3 · 105 mm
3 . Der Wert
P LT
4
von M∞ = 25 · 10 mm2 wurde in der Arbeit von Koerfer [24] ermittelt.
Bei der Angabe der maximalen Anzahl der Thrombozyten auf der Oberfläche muss berücksichtigt werden, dass die Thrombozyten sehr unterschiedliche Formen annehmen können.
In der Abbildung 5.11 a) ist ein inaktivierter Thrombozyt dargestellt, Abbildung b) zeigt
einen aktivierten Thrombozyten und Abbildung c) zeigt einen an der Oberfläche adhärierten Thrombozyten. Aus den drei Abbildungen wird deutlich, dass die Form des Thrombozyten eine entscheidende Rolle bei der Berechnung der Höhe des Thrombenbewuchses
spielt.
(a) Inaktiviertes Blutplättchen
(b) Aktiviertes Blutplättchen
(c) Adhäriertes Blutplättchen
Abbildung 5.11: Unterschiedliche Stadien eines Blutplättchens [5]
Da in den experimentellen Arbeiten von Ku und Flannery [26] keine Aussage über das
Anhaftverhalten der Thrombozyten getroffen wurde, sowie keine aussagekräftigen Bilder
vorhanden sind, müssen Annahmen zum Verhalten der Blutplättchen getroffen werden.
In der Abbildung 5.12 sind an einer mit Kollagen beschichteten Oberfläche adhärierte
Thrombozyten aus einem Experiment dargestellt [5]. Die Aufnahmen stammen aus einem
Fließkammerversuch der in [5] genauer beschrieben ist und für den bei einer Spaltbreite
von 200 µm eine Wandscherrate von 1000 s−1 herrscht. Es ist zu erkennen, dass diese
kugelförmig und nicht flach an der Oberfläche anhaften. Aus diesem Grund wird auch in
der Simulation die Annahme getroffen, dass die Thrombozyten kugelförmig anhaften. Als
Durchmesser wird ein Wert von 2.25 µm angenommen.
Abbildung 5.12: An Kollagen adhärierte Thrombozyten [5]
5.7. Berechnung des Thrombozytenwachstums
69
Mit diesen Werten kann auch die Anzahl der benötigten Schichten bis zum Verschluss
berechnet werden. Bei einem Durchmesser von 700 µm zu Beginn der 78% Stenose und
einem Durchmesser der Blutplättchen von 2,25 µm sind somit 311,11 Schichten nötig um
die Arterie zu verschließen.
Die Anzahl der Thrombozyten pro 1000 µm2 kann mit folgender Gleichung berechnet
werden:
N = 250 · (1 − dof_1) + 250 · (1 − dof_1) · dof_2
(5.19)
Dabei ist N die Anzahl der adhärierten Plättchen pro 1000 µm2 , dof_1 der prozentuale
Anteil der freien Oberfläche an der Wand, und dof_2 die prozentuale Anzahl weiterer
Schichten. Die Zahl 250 rührt daher, dass wie schon erwähnt, dass auf einer Fläche von
1000 µm2 250 Plättchen anhaften können [24].
Die Anfangskonzentrationen von RP, AP und ADP im Einströmgebiet müssen zu Beginn
der Rechnung festgelegt werden. Die Konzentration von ADP wird dabei immer zu Null
gesetzt. Für die Konzentrationen der RP wird ein Wert von 0,45 und für die AP ein Wert
von 0,35 angenommen. Die Konzentrationen ergeben zusammen keine 100%, da davon
ausgegangen wird, dass 20% der Plättchen nicht aktiviert werden können. Diese Werte
werden nur als Startwerte angenommen, da eine lineare Abhängigkeit vorliegt, also mit
Erhöhung der Konzentration der AP die Anhaftung der Bluttplättchen um den gleichen
Faktor steigt, können die Werte anschließend angepasst werden. In der Tabelle 5.5, ist am
Beispiel von zwei Rechnungen zu einer 95,9% Stenose aufgezeigt, dass sich mit Verdoppelung der Anfangskonzentration von AP, sich auch die Schichtzunahme pro Zeit verdoppelt
und somit ein linearer Zusammenhang vorliegt.
Tabelle 5.5: Einfluss der Konzentration von AP am Beispiel einer 95,9% Stenose
[AP]0
Schichtwachstum pro Zeit [ Schicht
]
s
0,35
0,1143
0,7
0,228
5.7 Berechnung des Thrombozytenwachstums
Ziel der Simulation ist es, die Kennzahl für die Reaktionskonstanten kaa in Abhängigkeit
von der Scherrate zu ermitteln. Gleichzeitig muss ein Zusammenhang der Inflow Konzentrationen von RP und AP in Bezug zur Scherrate festgelegt werden.
5.7. Berechnung des Thrombozytenwachstums
70
Die Werte sollen dabei so ermittelt werden, dass das Thrombozytenwachstum den gleichen
Verlauf wie im Experiment von Ku und Flannery aufweisen [26] (siehe auch Abbildung 5.8).
In der Abbildung 5.13 sind die verschiedenen Stenosen, von denen jeweils die Rechnung
gestartet werden soll, dargestellt.
(a) 78,47%Stenose (b) 81,90%Stenose (c) 89,97%Stenose (d) 95,90%Stenose
(e) 99,34%Stenose
Abbildung 5.13: Geometrien der unterschiedlichen Startstenosen
Zunächst wird die erste Schicht der Geometrie vollständig bedeckt. Dabei spielen vor allem
die Reaktionskonstanten krs und kas eine Rolle, diese können aber nicht zu groß gewählt
werden, da ansonsten die Rechnung abbricht. Aus diesem Grund wird die erste Schicht,
in einer beliebigen Zeit und klein genug gewählten Werten von krs und kas , bedeckt. In
dieser Arbeit wurde bei allen fünf Stenosen für krs = 0, 15, für kas = 0, 4 und kaa = 0, 2245
gesetzt. Bei der Stenose von 99,3 % kommt es aber bei der Verwendung von diesen Werten
zu einem Abbruch der Rechnung. Aus diesem Grund wurden bei dieser, zur Bedeckung
der ersten Schicht, für die Reaktionskonstanten folgende Werte gewählt: krs = 0, 08 , für
kas = 0, 09 und kaa = 0, 03.
Ist die erste Schicht bedeckt, erfolgt ein Restart der Rechnung und es spielt nur noch die
Reaktionskonstante kaa eine Rolle. Bei dem Restart der Rechnung muss beachtet werden,
dass sich sowohl “data.all”, als auch “s.all” in dem Ordner der Rechnung befinden müssen.
Auch ntsbout darf nicht zu Null gesetzt sein, da ansonsten “s.all” nicht ausgegeben wird.
Das XNS Input File sieht bei 11 Einträgen im “data.all” folgendermaßen aus:
restart on
data.in data.all1
nrec 11
Zusätzlich muss beachtet werden, dass bei der Anschlussrechnung die Daten im “data.all”
und “s.all” nach und nach überschrieben werden und wenn bei der Folgerechnung weniger
ausgeschrieben wird als bei der vorherigen, auch nur dieser Teil im Daten File überschrieben wird, und somit noch immer alte Daten im “data.all” vorhanden sind.
Bei der Ermittlung der Reaktionskonstante kaa wird auf die Experimente von Ku und
Flannery [26] zurückgegriffen. In der Tabelle 5.6 sind die Werte zu den fünf Stenosen von
denen jeweils eine Rechnung gestartet werden soll dargestellt. Dazu sind in der Tabelle die
radialen Differenzen zwischen der gerade betrachteten Stenose und der darauf folgenden
angegeben, also der Bereich der mit Thrombozyten belegt werden soll. Aus dieser Größe
5.7. Berechnung des Thrombozytenwachstums
71
lässt sich, mit einem Durchmesser der Thrombozyten von 2,25 µm, die erforderlich Anzahl
an Schichten bestimmen. Zusätzlich ist in der Tabelle die Zeit, die zwischen zwei Stenosen
liegt, angegeben. Daraus lässt sich die durchschnittliche Zeit pro Schicht die benötigt wird
bestimmen. Die maximale Scherrate, die bei der Strömungsberechnung bestimmt wurde,
wird benötigt um die verstärkte Diffusivität Ds (siehe Gleichung 5.16) zu bestimmen. Für
die Konstanten kaa , [RP ]0 und [AP ]0 werden bei allen Stenose die gleichen Werte gewählt.
Diese können später angepasst werden, da zwischen diesen und der durchschnittlichen Zeit,
die pro Schicht benötigt wird, ein linearer Zusammenhang vorliegt.
Tabelle 5.6: Angabe der Rechnungsgrößen zu den unterschiedlichen Stenosen
Stenose [%]
78,5
81,90
89,90
95,9
99,3
Differenz zum Radius
der nächsten Stenose
[µm]
34,94
81,02
86,02
91,3
60,5
Anzahl erforderlicher
Schichten (Auf den
Radius bezogen)
15,53
36,01
38,31
40,58
26,89
Zeit [s]
144
352,2
247,8
103,8
137,4
Zeit pro Schicht
s
[ Schicht
]
9,27
9,48
6,47
9,81
5,11
γmax [s−1 ]
25 794
27 406
31 654
36 854
21 867
Ds [10−3 · mm
]
s
4,1377
4,396
5,078
5,91
3,51
krs [ m
s]
0,15
0,15
0,15
0,15
0,08
kas [ m
s]
0,4
0,4
0,4
0,4
0,09
kaa [ m
s]
0,2245
0,2245
0,2245
0,2245
0,2245
[RP ]0
0,45
0,45
0,45
0,45
0,45
[AP ]0
0,35
0,35
0,35
0,35
0,35
2
In der Abbildung 5.14 a) sind die maximalen Scherraten über der jeweiligen Stenose aufgetragen. Abbildung b) zeigt den Verlauf der Scherrate für eine 89,97% Stenose auf.
Stenose
78,5
81,9
89,9
95,9
99,3
Scherrate
25794
27406
31654
36854
21867
0,162
0,148
0,184
0,101
0,373
5.8. Auswertung des reaktionsgesteuerten Schichtwachstums
72
Simulation einer Stenose Strömungsberechnung
40000
Scherrate [1/s]
36000
32000
28000
Strömungsberechnung (2)
• Auswertung der Scherraten
78,5
81,9
89,9
95,9
99,3
25794
27406
31654
36854
21867
0,162
0,148
0,184
0,101
0,373
(Ausgabe in XNS durch ss.all)
24000
20000
80
85
90
95
100
38000
Stenose [%]
36000
34000
(a) Maximale Scherraten bei den verschiedenen Stenosen (b) Verlauf der Scherrate für eine 89,97% Stenose
32000
30000
Abbildung 5.14: Scherrate
28000
26000
24000
0,4
22000
20000
75
80
85
90
95
100
0,3
Scherrate [1/s ]
75
5.8 Auswertung des reaktionsgesteuerten Schichtwachstums
Nachdem bei allen fünf Stenosen die erste Schicht bedeckt wurde und ein Neustart der
Stenose [%]
Rechnung mit der in der Tabelle 5.8 angegeben Werten durchgeführt wurde, kann eine
0,2
23
02 Juli 2010
Stephanie
Schmitz
Auswertung
der Ergebnisse erfolgen.Diplomvortrag
Bei jeder -der
Rechnungen
wurde ein Mittelwert
aus
0,4
5 Werten
für das durchschnittliche Wachstum pro Schicht berechnet. Diese Mittelwerte
0,1
0,35
weichen maximal um 0,15% voneinander ab. In der Tabelle 5.7 sind die durchschnittlichen
0,3
0
Zeiten
aufgelistet.
0,25
0,2
Tabelle 5.7: Durchschnittliches Wachstum der Schichten bei den unterschiedlichen Steno0,15
sen
0,1
0,05
0
Stenose
[%]75
70
78,5
Durchschnittlicher
Schichtwachstum
*85
+ pro Zeit
80
90
95
Schicht
Sekunde
0,11452
Durchschnittliche
Zeit
*
+
pro Schicht Sekunde
Schicht
100
8,73
81,9
0,11424
8,75
89,9
0,11336
8,82
95,9
0,11434
8,75
99,53
0,11227
8,91
Aus der Tabelle kann entnommen werden, dass trotz der sehr unterschiedlichen Scherraten
und Volumenströme, die durchschnittlichen Zeiten bei allen Stenosen ungefähr in einem
Bereich liegen. Das liegt daran, dass ab Scherraten von über 1300 s−1 die Anhaftung
5.8. Auswertung des reaktionsgesteuerten Schichtwachstums
73
der Thrombozyten nicht mehr Diffusions-, sondern Reaktionsgesteuert ist [29]. In der
Strömung liegen genug Thrombozyten vor, sodass die Bildung der Schichten nicht mehr
von der Fließgeschwindigkeit, sondern nur noch von der Reaktionsrate kaa abhängt, die
dafür sorgt dass die Blutplättchen anhaften.
Aktivierungsgrad der Inflowkonzentrationen
Um die Werte für kaa bestimmen zu können, muss zunächst der lineare Zusammenhang
zwischen den Inflowkonzentrationen [RP ]0 und [AP ]0 und der Scherrate γ̇ bestimmt werden. Da dieser nicht bekannt ist, muss er festgelegt werden. So wird die Inflowkonzentration von [AP ]0 bei einer Scherrate von 21 000 s−1 auf 0,35 und bei 37 000 s−1 auf 0,7
gesetzt. Diese Werte für den Aktivierungsgrad sind geschätzt und müssten idealerweise
experimentell bestimmt werden. In dem Diagramm 5.15 sind beide Größen übereinander aufgetragen. [AP ]0 und [RP ]0 können für die jeweilige Scherrate γ̇ mit den folgenden
Gleichungen berechnet werden:
[AP ]0 = 0, 35 + (γ̇ − 21000) ·
0, 35
16000
[RP ]0 = 0, 8 − [AP ]0
(5.20)
(5.21)
Abbildung 5.15: Konzentration von [AP ]0 in Abhängigkeit der Scherrate
In der Tabelle 5.8 sind für die Stenosen die zunächst festgelegten Werte für [AP ]0 mit
einem Sternchen ∗ gekennzeichnet, die neu berechneten mit zwei Sternchen ∗∗ . Es wird
nur der Parameter AP betrachtet, da mit dessen Steigerung die Schichtzunahme pro Zeit
proportional zunimmt. [RP ]0 nimmt mit steigendem [AP ]0 ab und besitzt keinen Einfluss
auf die Anhaftung der Thrombozyten.
In der dritten Spalte ist der Skalierungsfaktor dargestellt. Dieser berechnet sich aus der
∗
Division des neuen [AP ]∗∗
0 durch das alte [AP ]0 . Die benötigte Zeit zur Bedeckung einer
5.8. Auswertung des reaktionsgesteuerten Schichtwachstums
74
Schicht nimmt proportional zur Steigerung der [AP ]0 ab, so dass die aus den Simulationen
erhaltene Zeit zur Bedeckung einer Schicht mit Thrombozyten (Spalte 5, mit einem Sternchen ∗ gekennzeichnet) durch den Skalierungsfaktor dividiert wird. In der letzten Spalte
der Tabelle sind die neu berechneten Zeiten (mit einem Sternchen ∗∗ gekennzeichnet) festgehalten.
Tabelle 5.8: Angaben zur Ermittlung der benötigten Zeit für die Bedeckung einer Schicht
Stenose
[%]
[AP]∗0
[AP]∗∗
0
Skalierungsfaktor
Zeit pro
Schicht ∗
Zeit pro
Schicht ∗∗
78,5
0,35
0,4549
1,30
8,73
6,72
81,9
0,35
0,4901
1,40
8,75
6,25
89,9
0,35
0,5830
1,67
8,82
5,28
95,9
0,35
0,6968
1,99
8,75
4,40
99,3
0,35
0,3690
1,05
8,91
8,49
Ermittlung der Reaktionskonstanten kaa
Mit diesen neuen Zeiten können nun die Werte für die Konstante kaa ermittelt werden.
Tabelle 5.9: Angaben zur Ermittlung der Konstante kaa
Stenose
[%]
Ermittelte
s
Zeit [ Schicht
]
Ermittelte
Zeit nach
s
[26] [ Schicht
]
Skalierungsfaktor
∗
kaa
∗∗
kaa
78,5
6,72
9,27
0,72
0,2245
0,162
81,9
6,25
9,48
0,66
0,2245
0,148
89,9
5,28
6,47
0,82
0,2245
0,184
95,9
4,40
9,81
0,45
0,2245
0,101
99,3
8,49
5,11
1,66
0,2245
0,373
In der Tabelle 5.9 sind diese in der letzten Spalte mit zwei Sternchen ∗∗ gekennzeichnet.
Ermittelt werden diese, in dem zunächst die in Tabelle 5.8 angegebenen, neu berechneten
Zeiten (in der Tabelle 5.9 Spalte 2), durch die von Ku und Flannery [26] bestimmten Zeiten
(Spalte 3) dividiert werden. Dadurch wird ein neuer Skalierungsfaktor erhalten (Spalte 4),
5.8. Auswertung des reaktionsgesteuerten Schichtwachstums
75
mit Hilfe dessen nun die neuen Werte für die Konstante kaa ermittelt werden können.
∗ ) mit dem
Dazu werden die zunächst in der Simulationen angegeben Werte (Spalte 5, kaa
Skalierungsfaktor multipliziert und somit die in der letzten Spalte aufgeführten Werte für
kaa erhalten. In dem Diagramm 5.16 sind die ermittelten Reaktionsraten noch einmal für
die unterschiedlichen Stenosen aufgetragen.
0,45
0,373
k_aa
0,338
0,225
0,162
0,184
0,148
0,101
0,113
0
78,5
81,9
89,9
95,5
99.3
Stenose [%]
Abbildung 5.16: kaa Werte bei den unterschiedlichen Stenosen
Ziel dieser Simulation war es jedoch die Reaktionsraten in Abhängigkeit der Scherraten zu
bestimmen. In dem Diagramm 5.17 ist die Reaktionsrate über der Scherrate aufgetragen.
In dem Diagramm ist zu erkennen, dass mit zunehmender Scherrate die Reaktionsrate
abnimmt, also insgesamt weniger Thrombozyten anhaften können. Genähert wurde die
Kurve durch eine hyperbolische Funktion, welche durch folgende Gleichung beschrieben
wird:
kaa =
a
γ̇ − b
(5.22)
Die Koeffizienten wurden durch eine Optimierungsmethode ermittelt, bei der der Least
Square Fehler in Bezug auf die vorhandenen Datenpaare minimiert wird, so dass sich
folgende Gleichung ergibt:
1800
kaa =
(5.23)
γ̇ − 16905
In dem Diagramm 5.17 sind die numerisch ermittelten Werte durch die blauen Kreuze dargestellt und die schwarze Kurve stellt eine polynomische Näherungskurve zweiter Ordnung
dar. Die bessere Näherungskurve entspricht jedoch der eben beschriebenen hyperbolischen
Funktion und wird durch die rote Kurve dargestellt.
76
kaa
5.8. Auswertung des reaktionsgesteuerten Schichtwachstums
Scherrate [1/s]
Abbildung 5.17: kaa Werte aufgetragen über der Scherrate
Somit konnte das Ziel, eine Methodik zu entwickeln um die Reaktionsrate in Abhängigkeit der Scherrate darzustellen, erfüllt werden. Im Bereich hoher Scherraten von 22 000
- 37 000 s−1 nimmt die Reaktionsrate kaa mit steigender Scherrate ab. Das heisst, dass
trotz des bei hohen Scherraten gut funktionierenden vWF weniger Thrombozyten mit
steigender Scherrate anhaften können und somit die für die Adhäsion ungünstige kurze Kontaktzeit, die bei hohen Scherraten im Bereich der Stenose vorliegt, einen starken
begrenzenden Einfluss auf das Anhaftverhalten der Thrombozyten besitzt.
Im nächsten Kapitel erfolgt die Zusammenfassung der Arbeit, und es werden mögliche
Ausblicke gegeben.
77
6 Zusammenfassung und Ausblick
Im Rahmen dieser Diplomarbeit wurden zwei unterschiedliche numerische Simulationen
durchgeführt. Die erste Simulation beschäftigte sich mit den sich zeitlich veränderlichen
Geometrien und der Strömung des linken menschlichen Ventrikels. Im zweiten Teil der Arbeit wurde das Anhaftverhalten von Thrombozyten unter dem Einfluss von hohen Scherraten unter Verwendung der ADR Gleichungen untersucht.
Die Simulation des linken Ventrikel des menschlichen Herzens stellte sich als sehr komplex
heraus. Bereits bei der Netzerstellung, der aus den MRT Daten extrahierten Geometrien kam es anfänglich zu Problemen. Nachdem eine einheitliche Topologie sichergestellt
werden konnte, war die Erstellung der Volumengitter möglich. Alle 30 extrahierten Geometrien konnten mittels der EMUM hintereinander geschaltet werden und es bedurfte
dabei zwischen keinem der Schritte einer Datenprojektion. Anschließend konnten erste
Strömungsuntersuchungen durchgeführt werden.
Eine denkbare weiterführende Arbeit wäre somit die Strömungen im Herzen weiter zu betrachten, so dass der gesamte Zyklus simuliert und ausgewertet werden kann. Außerdem
könnte die Simulation der Klappenbewegung mitbetrachtet werden. Zusätzlich kann versucht werden nicht nur das Ventrikel, sondern auch die Aorta und weitere Anschlussgefäße
an die Simulation zu koppeln. Eine weitere mögliche Fortsetzung der Arbeit könnte die
Untersuchung der Interaktion von Struktur und Strömung sein.
Der zweite Teil der Arbeit beschäftigte sich mit der Simulation des Verschlusses einer
Koronararterie. Ziel der Untersuchung war es, eine Methodik zur Bestimmung der benötigten Reaktionsraten in Abhängigkeit von der Scherrate zu entwickeln, so dass für den
Verschluss der Stenose die gleiche Zeit wie in der experimentellen Untersuchung von Ku
und Flannery [26] benötigt wurde.
Für die Simulation wurden zunächst die Geometrien der unterschiedlichen Stenosen erstellt und vernetzt. Anschließend wurden die Strömungen in den verschiedenen Stenosen
berechnet und die Scherraten betrachtet. Für den scherratenabängigen Aktivierungsgrad
der Thrombozyten wurden aufgrund fehlender empirischer Daten Annahmen getroffen.
Darauf aufbauend wurden für alle Konfigurationen die ADR Gleichungen gelöst und ausgewertet. Bei den Auswertungen konnte festgestellt werden, dass mit zunehmender Scherrate
die Reaktionsrate abnimmt, und somit weniger Thrombozyten an der Oberfläche anhaften
78
können. Der gesuchte funktionelle Zusammenhang zwischen Reaktionsrate und Scherrate
konnte schließlich ermittelt werden.
Eine mögliche Fortsetzung wäre die Weiterentwicklung der ADR Gleichungen, d.h. die
Implementierung der hier ermittelten scherratenabhängigen Adhäsionsraten und Thrombozytenaktivierung. Zusätzlich kann die hier aufgezeigte Methodik zur Bestimmung der
Reaktionsraten auch auf andere Experimente angewandt werden, um weitere Ergebnisse
zu produzieren. Dazu wäre es sinnvoll die Experimente mit Citrat versetztem Blut durchzuführen, damit ein besserer Vergleich zum numerischen Modell möglich ist. Eine höhere
zeitliche Auflösung der Versuche mit mehr Messpunkten würde es ermöglichen genauere
numerische Ergebnisse zu produzieren.
79
Eidesstattliche Erklärung
Hiermit versichere ich, die vorliegende Arbeit selbständig und unter ausschließlicher Verwendung der angegebenen Literatur und Hilfsmittel erstellt zu haben.
Die Arbeit wurde bisher in gleicher oder ähnlicher Form keiner anderen Prüfungsbehörde
vorgelegt und auch nicht veröffentlicht.
Aachen, Juli ..., 2010
Stephanie Schmitz
80
Literaturverzeichnis
[1] Affeld, K.:
Strömungsmechanik in der Medizin - Biofluidmechanik.
online. –
URL http://www.charite.de/biofluidmechanik/downloads/
SkriptBiofluidmechanik1.pdf. – abgerufen: 02.03.2010
[2] Baccani, B. ; Domenichini, F. ; Pedrizzetti, G.: Vortex dynamics in a model
left ventricle during filling. In: European Journal of Mechanics - B/Fluids 21 (2002),
Nr. 5, S. 527 – 543
[3] Baccani, B. ; Domenichini, F. ; Pedrizzetti, G.: Model and influence of mitral
valve opening during the left ventricular filling. In: Journal of Biomechanics 36
(2003), Nr. 3, S. 355 – 361
[4] Bark, D.: Mechanistic numerical study of thrombus groth. Master Thesis am Georgia
Institute of Technology, 2007
[5] Behbahani, M. ; Waluga, C. ; Mai, A. ; Seweryn, L. ; Bergmann, B. ; Behr,
M. ; Tran, L. ; Vonderstein, K. ; Oedekoven, B. ; Mottaghy, K.: Simulation of
Blood Damage in Technical Devices: Experiment, Modeling and Numerical Simulation.
Kompetenzplattform Bioengineering talk at FH Aachen, 2009. – URL http://www.
cats.rwth-aachen.de:8080/~mb/announcement-fh-aachen2009.pdf
[6] Behr, M.: XNS Elastic Mesh Update. online. – URL http://www.cats.
rwth-aachen.de/software/simulation/xns/elastic/view?searchterm=
poisson. – abgerufen: 16.06.2010
[7] Berg, F.: Angewandte Physiologie, Bd.2, Organsysteme verstehen und beeinflussen.
Thieme, Stuttgart, 2000
[8] Claeßens, D. ; Faouzi, H. ; Mayer, D.: Numerische Simulation einer TaylorCouette Strömung und Modellierung thrombozytärer Reaktionen. Projektarbeit am
Lehrstuhl für computergestützte Analyse technischer Systeme an der RWTH Aachen,
2009
[9] Despopoulos, A. ; Silbernagl, S.: Taschenatlas der Physiologie. Thieme Stuttgart,
2007
Literaturverzeichnis
81
[10] Dierberger, B.: Finite-Elemente-Simulation der Herzdynamik das HerzgrößenSchlagvolumen-Konzept. Dissertation an der Eberhard Karls-Universität Tübingen,
1993
[11] Donea, J. ; Huerta, A.: Finite Element Methods for Flow Problems. Wiley, 2003
[12] Ferziger, J.H. ; Peric, M.: Numerische Strömungsmechanik. Springer-Verlag Berlin
Heidelberg, 2008
[13] Flannery, C.: Thrombus formation under high stress in arterial stenotic flow. Master Thesis am Georgia Institute of Technology, 2005
[14] Fung, Y. C.: Biomechanics: Mechanical Properties of Living Tissues. 2nd. Springer,
6 1993. – ISBN 9780387979472
[15] Gray, H. (Hrsg.): Gray’s Anatomy. Lea an Febinger, 1918
[16] H. Löwel : Koronare Herzkrankheit und akuter Myokardinfarkt [Gesundheitsberichterstattung - Themenhefte]. 2006
[17] Helmholtz Institute für angewandte Medizintechnik: Cardiovascular Engineering. – URL http://www.ame.hia.rwth-aachen.de/
[18] Hick, C. ; Hick, A.: Intensivkurs Physiologie. 6., überarbeitete Auflage. Elsevier,
München, 2009
[19] Hughes, T.J. R.: The Finite Element Method: Linear Static and Dynamic Finite
Element Analysis. Dover Publications, 2000
[20] Jaminet, P.: Bifunktionale Fusionsporteine: Kombination hochselektiver, direkter
Faktor XA Inhibition mit aktivationsspezifischer GP2b/3a Blockade einerseits, und
zielgerichtetem Fibrin-Targeting andererseits. Dissertation an der Medizinischen Fakultät der Albert-Ludwigs-Universität Freiburg in Breisgau, 2004
[21] Kilner, P. J. ; Yang, G. Z. ; Wilkes, A. J. ; Mohiaddin, R. H. ; Firmin, D. N. ;
Yacoub, M. H.: Asymmetric redirection of flow through the heart. In: Nature 404
(2000), S. 759–761
[22] Klinke, R. ; Pape, H.-C. ; Kurtz, A. ; Silbernagl, S.: Physiologie: Lehrbuch. 5.
vollständig überarbeitete Auflage. Thieme, Stuttgart, 2005
[23] Klinke, R. ; Pape, H-C. ; Silbernagl, S.: Physiologie. Thieme Stuttgart, 2005
[24] Koerfer, S.: Der Einfluss von laminaren Strömungen und Sekundärströmungen
im Taylor-Couette-System auf die Thrombozyten. Dissertation an der Fakultät für
Mathematik, Informatik und Naturwissenschaften der RWTH Aachen, 2002
Literaturverzeichnis
82
[25] Krause, E.: Strömungslehre, Gasdynamik und Aerodynamisches Laboratorium. Teubner B.G. GmbH, 10 2003
[26] Ku, D.N. ; Flannery, C.J.: Development of a flow through system to create occluding thrombus. In: Biorheology 44 (2007), S. 273–284
[27] Lemmon, J. D. ; Yoganathan, A.P.: Computational modeling of left heart diastolic function: examination of ventricular dysfunction. In: Journal of Biomedical
Engineering 122 (2000), Nr. 4, S. 297–303
[28] Long, Q. ; Merrifield, R. ; Yang, G. Z. ; Kilner, P. J. ; Firmin, D.N. ; Xu, X.Y.:
The influence of inflow boundary conditions on intra left ventricle flow predictions.
In: Journal of Biomechanical Engineering 125 (2003), December, Nr. 6, S. 922–927
[29] Mai, N.A.: Numerical simulation of blood flow and shear-dependent platelet adhesion.
Bachelor Arbeit am Lehrstuhl für computergestützte Analyse technischer Systeme an
der RWTH Aachen, 2010
[30] Mandinov, L. ; Eberli, F. R. ; Seiler, C. ; Hes, O. M.: Diastolic heart failure. In:
Cardiovascular Research 45 (2000), Nr. 4, S. 813 – 825
[31] McQueen, D. M. ; Peskin, C. S.: Heart Simulation by an Immersed Boundary Method with Formal Second-order Accuracy and Reduced Numerical Viscosity (article).
In: Mechanics for a New Mellennium, Springer Netherlands, 2001, S. 429 –444
[32] Oertel, H.: Bioströmungsmechanik: Grundlagen, Methoden und Phänomene. 1.
Vieweg+Teubner, 2008
[33] Oertel, H. ; Krittian, S. ; Spiegel, K.: Modelling the human cardiac fluid mechanics. 3rd ed. Universitätsverlag Karlsruhe, Karlsruhe, 2009
[34] Oertel, H. ; Laurien, E.: Numerische Strömungsmechanik. Grundgleichungen und
Modelle - Lösungsmethoden - Qualität und Genauigkeit. Vieweg+Teubner Verlag,
2009
[35] Pedrizzetti, G. ; Domenichini, F.: Nature Optimizes the Swirling Flow in the
Human Left Ventricle. In: Phys. Rev. Lett. 95 (2005), Sep, Nr. 10, S. 108101
[36] Pointwise Inc.: Pointwise User Manual. 2007
[37] Pötzsch, B. (Hrsg.) ; Madlener, K. (Hrsg.): Hämostaseologie: Grundlagen, Diagnostik und Therapie. 2. Aufl. Springer, Berlin, 12 2009
[38] Reininger, A. J. ; Heijnen, H. F. G. ; Schumann, H. ; Specht, H. M. ; Schramm,
W. ; Ruggeri, Z. M.: Mechanism of platelet adhesion to von Willebrand factor and
Literaturverzeichnis
83
microparticle formation under high shear stress. In: Thrombosis Research 107 (2006),
Nr. 9, S. 3537 – 3545
[39] Rodenwaldt, J.:
Magnetresonanztomographie, Mehrschicht-Spiral-CT und
Elektronenstrahl-CT zur morphologischen und funktionellen Diagnostik der koronaren Herzkrankheit. Habiltation an der Humboldt-Universität zu Berlin, Medizinische
Fakultät - Universitätsklinikum Charité, 2003. – URL http://edoc.hu-berlin.de/
docviews/abstract.php?id=20149. – Online: Stand 2010-05-03T08:34:06Z
[40] Ruggeri, Z. M. ; Orje, J. N. ; Habermann, R. ; Federici, A. B. ; Reininger,
A. J.: Activation-independent platelet adhesion and aggregation under elevated shear
stress. In: Blood 108(6) (2006), S. 1903–1910
[41] Ruggeri, Z.M.: Von Willebrand factor: a matrix protein that tries to be soluble. In:
Blood 101 (2003), 4, S. 2450
[42] Russell, Dr. D. C.: Spinal Anatomy Overview. online. – URL http://drcaram.
com/spinal-anatomy-overview/. – abgerufen: 16.02.2010
[43] Saber, N. R. ; D.Gosman, A. ; Wood, N. B. ; Kilner, P. J. ; Charrier, C. L. ;
Firmin, D. N.: Computational flow modeling of the left ventricle based on in vivo
MRI data: initial experience. In: Journal of Biomedical Engineering 29 (2001), Nr. 4,
S. 275–283
[44] Sakariassen, K. S. ; Holme, P. A. ; Orvim, U. ; Barstad, R. M. ; Solum, N. O. ;
Brosstad, F.R.: Shear-induced platelet activation and platelet microparticle formation in native human blood. In: Thrombosis Research 92 (1998), Nr. 6, Supplement
2, S. 33 – 41
[45] Savage, B. ; Saldivar, E. ; Ruggeri, Z.: Initiation of Platelet Adhesion by Arrest
onto Fibrinogen or Translocation on von Willebrand Factor. In: Cell 84(2) (1996),
S. 289–297
[46] Schäfer, M. (Hrsg.): Numerik im Maschinenbau. Springer, Berlin, 1999
[47] Schneider, M.F. ; Schneider, S.W.: Der Willebrand-Faktor: ein intelligenter Gefäßkleber. In: Biospektrum 14 (2008), S. 134–138
[48] Schünke, M.: Der Körper des Menschen. Thieme Georg Verlag, 9 2004
[49] Seweryn, L. ; Behbahani, M.: XNS programming progress. Current project activities am Lehrstuhl für computergestützte Analyse technischer Systeme an der RWTH
Aachen, 2009
84
[50] Sorensen, E.N. ; Burgreen, G.W. ; Wagner, W.R. ; Antaki, J.F.: Computational Simulation of Platelet Deposition and Activation: I. Model Development and
Properties. In: Annals of Biomedical Engineering 27 (1999), S. 436–448
[51] Statisches Bundesamt Deutschland: Pressemitteilung Nr.344 vom 15.09.200.
online. – URL http://www.destatis.de/jetspeed/portal/cms/Sites/destatis/
Internet/DE/Presse/pm/2009/09/PD09__344__232,templateId=renderPrint.
psml. – abgerufen: 16.06.2010
[52] Steen, T. ; Steen, S.: Filling of a model left ventricle studied by colour M mode
Doppler. In: Cardiovascular Research 28 (1994), Nr. 12, S. 1821 – 1828
[53] Stock, S.: Numerische Simulation von Blutströmung und Blutschädigung für ausgewählte Testfälle. Diplomarbeit am Lehrstuhl für computergestützte Analyse technischer Systeme an der RWTH Aachen, 2009
[54] Vasan, R. S. ; Levy, D.: Defining Diastolic Heart Failure. In: Circulation 101 (2000),
S. S2118 – 2121
[55] Vierendeels, J.A. ; Riemslagh, K. ; Dick, E. ; Verdonck, P. R.: Computer
simulation of intraventricular flow and pressure gradients during diastole. In: Journal
of Biomechanical Engineering 122 (2000), Nr. 6, S. 677 – 684
[56] Waluga, C.: Numerical simulation of platelet adhesion, activation and aggregation.
Diplomarbeit am Lehrstuhl für computergestützte Analyse technischer Systeme an
der RWTH Aachen, 2008
[57] Young, D.F. ; Tsai, F. Y.: Flow characteristics in models of arterial stenoses. I.
Steady flow. In: Journal of biomechanics 165(1) (1973), S. 288–306
[58] Zydney, A.L. ; Colton, C.K.: Augmented solute transport in the shear flow of a
concentrated suspension. In: PhysicoChemical Hydrodynamics 10(1) (1988), S. 77–96
85
A Anhang
A.1 Strömungssimulation der Herzgeometrien
A.1.1 VRML 1.0 Format
In dem Format werden die drei Oberflächen (Aorten-, Mitralklappe und das linke Ventrikel) mit jeweils einem Block a) und b) beschrieben.
#VRML V1.0 ascii NormalBinding {
value PER_VERTEX_INDEXED
}
DirectionalLight {
direction -12000.000 -12000.000 -3000.000
color 1.000 1.000 1.000
intensity 0.700
DirectionalLight {
direction 12000.000 -6000.000 -12000.000
color 1.000 1.000 1.000
intensity 0.700
}
Separator{
Separator{
Material{
ambientColor 0.0000.2500.000
diffuseColor 0.0001.0000.000
specularColor 0.5000.5000.500
transparency 0.000
shininess 0.600
}Coordinate3{
point [
132.652116 − 176.395958 32.354591,
....]























































a)
A.1. Strömungssimulation der Herzgeometrien
IndexedFaceSet{
coordIndex[
2817, 2242, 2615, −1
2817, 2221, 2242, −1
2816, 2221, 2817, −1
....]























86
b)
Dabei beinhaltet der Block a) die Koordinaten der Knoten und Block b) definiert die drei
Knoten der Polygone (Dreiecke).
A.1.2 XNS Input File
A.1.2.1 Verschiebung - “mshift” Input
# title Herz Verschiebung
# Mesh input
source minf
mien mien
mrng mrng
mshift mshift
mxyz mxyz
smallshift 0.01
nprmread on
#restart on
restart off
ntsbout 10
timing on
debug on
dt 0.0003
moving on
surface_movement shift
# Solve parameters
ninner 100
nouter 5
nit 5
A.1. Strömungssimulation der Herzgeometrien
87
# Data storage paramters
nsd 3
nen 8
# Time discretization
nts 101
steady off
space-time on
#semi-discrete
# Formulation selection
stokes off
# stabilization parameters
tau_momentum shakib
tau_momentum_factor 1.0
tau_continuity_factor 1.0
element_length diagonal
# Turbulence model
turbulence_model none
# Material properties # all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas
material 1 viscosity 3.4
material 1 density 1.0
# wall (11)
rngdset 11 1 1 1
# inflow (12)
rngdflux 12 0.9866 0.9866 0.9866
# outflow (13)
rngdset 13 1 1 1
rngdflux 13 9.81 9.81 9.81
# mesh boundary conditions
rngxset 11 1 1 1
rngxset 12 1 1 1
rngxset 13 1 1 1
A.1. Strömungssimulation der Herzgeometrien
# Write out fluxes
flux_scale 12 +1.0
flux_scale 13 +1.0
A.1.2.2 Instationäre Rechnung
# Mesh input
source minf
mien mien
mrng mrng
mxyz mxyz
nprmread on
restart off
ntsbout 50
timing on
debug on
dt 0.0003
# Solve parameters
ninner 100
nouter 5
nit 5
# Data storage paramters
nsd 3
nen 8
# Time discretization
nts 150
steady off
space-time on
#semi-discrete
# Formulation selection
stokes off
# stabilization parameters
tau_momentum shakib
tau_momentum_factor 1.0
88
A.1. Strömungssimulation der Herzgeometrien
tau_continuity_factor 1.0
element_length diagonal
# Turbulence model
turbulence_model none
# Material properties
# all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas
material 1 viscosity 3.4
material 1 density 1.0
# wall (11)
rngdset 11 1 1 1
# inflow (12)
rngdflux 12 756144 756144 756144
# outflow (13)
# Write out fluxes
flux_scale 12 +1.0
flux_scale 13 +1.0
A.1.2.3 Stationäre Rechnung
# Mesh input
source minf
mien mien
mrng mrng
mxyz mxyz
nprmread on
restart off
ntsbout 1
timing on
debug on
dt 0.0003
# Solve parameters
ninner 100
nouter 5
nit 100
89
A.1. Strömungssimulation der Herzgeometrien
# Data storage paramters
nsd 3
nen 8
# Time discretization
nts 1
steady on
space-time on
#semi-discrete
# Formulation selection
stokes off
# stabilization parameters
tau_momentum shakib
tau_momentum_factor 1.0
tau_continuity_factor 1.0
element_length diagonal
# Turbulence model
turbulence_model none
# Material properties
# all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas
material 1 viscosity 34000
material 1 density 1.0
# wall (11)
rngdset 11 1 1 1
# inflow (12)
rngdflux 12 756144 756144 756144
# outflow (13)
# Write out fluxes
flux_scale 12 +1.0
flux_scale 13 +1.0
90
A.2. Koronararterie
A.2 Koronararterie
A.2.1 Verschiebung - “mshift” Input
# title Stenose - Verschiebung
source minf
mien mien
mshift mshift
mrng mrng
mxyz mxyz
timing on
debug
#nprmsave on
nprmread on
recover on
restart on
data.in data.out1
mxyz.in mxyz1
moving on
surface_movement shift
smallshift 0.001
ninner 100
nouter 7
nsd 3
nen 8
stokes off
steady off
#semi-discrete
space-time on
nit 5
nts 1000
ntsbout 10
dt 0.001
91
A.2. Koronararterie
92
tau_momentum shakib
tau_momentum_factor 1.0
tau_continuity_factor 1.0
element_length diagonal
# all units in kg, mm, sec ausgehend von dyn Visk=3.8mPas
material 1 viscosity 3.6715
material 1 density 1.0
# mesh boundary conditions
rngxset 11 1 1 1
rngxset 12 1 1 1
rngxset 13 1 1 1
# inflow (11)
rngdset 11 1 1 1
rngdexp 11 3 (-1)*531.93*(1-(((x*x)+(y*y))/(0.5625)))
# outflow (12)
rngdset 12 1 1 0
# wall (13)
rngdset 13 1 1 1
turbulence_model none
# Write out fluxes
flux_scale 11 +1.0
flux_scale 12 +1.0
A.2.2 XNS Input File für die Strömungsberechnung am Bespiel der 81,90 %
Stenose
title Stenose - Strömung
source minf
mien mien
mrng mrng
mxyz mxyz
timing on
debug
A.2. Koronararterie
#nprmsave on
nprmread on
recover on
restart off
ninner 100
nouter 7
nsd 3
nen 8
stokes off
steady off
space-time on
nit 5
nts 250
ntsbout 50
dt 0.01
tau_momentum shakib
tau_momentum_factor 1.0
tau_continuity_factor 1.0
element_length diagonal
# all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas
material 1 viscosity 3.40265
material 1 density 1.0
# mesh boundary conditions
rngxset 11 1 1 1
rngxset 12 1 1 1
rngxset 13 1 1 1
# inflow (11)
rngdset 11 1 1 1
rngdexp 11 3 (-1)*437.55*(1-(((x*x)+(y*y))/(0.5625)))
# outflow (12)
rngdset 12 1 1 0
# wall (13)
rngdset 13 1 1 1
93
A.2. Koronararterie
94
turbulence_model none
# Write out fluxes
flux_scale 11 +1.0
flux_scale 12 +1.0
A.2.3 XNS Input File für die ADR Gleichungen nach Belegung der 1.Schicht
am Beispiel der 81,90% Stenose
title Stenose
source minf
mien mien
mrng mrng
mxyz mxyz
timing on
debug off
#nprmsave on
nprmread
restart on
data.in data.all nrec 9
ninner 100
nouter 8
nsd 3
nen 8
ndf 3
laplace off
steady off
space-time on
advection
nit 5
nts 5
ntsbout 1
dt 1
tau_momentum shakib
tau_momentum_factor 1.0
A.2. Koronararterie
95
tau_continuity_factor 1.0
element_length diagonal
# all units in kg, mm, sec ausgehend von Helmholtz dyn Visk=3.6mPas #material 1
viscosity 3.40265 #material 1 density 1.0
# ambient velocity from pre-computed stagnation point flow
daux data.aux
ambient steady
# 1=RP 2=AP 3=ADP 4=Aggregates
material 1 viscosity 4.396e-03
material 2 viscosity 4.396e-03
material 3 viscosity 2.57e-04
initexp 1 0.0
initexp 2 0.0
initexp 3 0.0
platelet_model adr_1 3.6 0.000
# New configuration input for k-value in XNS-Stock:
#for krs
kexp 13 1 0.7143 ((1.5e-01)*heaviside(-16.18-z)*heaviside(z+18.45))
#shear-dependent reactio rate as a functio of the coordinates:
#for kas
kexp 13 2 0.7143 ((4.00e-01)*heaviside(-16.18-z)*heaviside(z+18.45))
#for kaa
kexp 13 3 0.7143 ((2.245e-01)*heaviside(-16.18-z)*heaviside(z+18.45))
# inflow (11)
rngdset 11 1 1 1
rngdexp 11 1 0.475
rngdexp 11 2 0.1
rngdexp 11 3 0.0
A.3. Datenstruktur
A.3 Datenstruktur
A.3.1 Herz
• Gerechnet auf Jugene “hac098” im Ornder “HEART”
• Letztes verwendetes Gitter: Gitter Nr.11
• Alle Informationen in: “Documentation-2”
A.3.2 Koronararterie
• Gerechnet auf Jugene “hac098” im Ornder “Deforming_vessel”
• Letztes verwendetes Gitter: “NewMesh”
• Alle Informationen in: “Documentation-2”
96