1. Oszilloskop

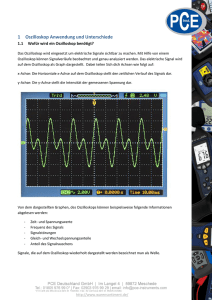
1.
Oszilloskop
Grundlagen
Ein Oszilloskop ist ein elektronisches Messmittel zur grafischen Darstellung von schnell
veränderlichen elektrischen Signalen in einem kartesischen Koordinaten-System (XY- Darstellung) als Kennlinie oder Zeitfunktion.
Funktion
Die aus der Kathodenröhre (1) austretenden Elektronen werden dort
durch
eine
Beschleunigungsspannung auf die Geschwindigkeit
vA beschleunigt. Der Elektronenstrahl passiert den Ablenkkondensator (2), wo die Messspannung ein
elektrisches Feld erzeugt, das den Strahl um den Winkel α ablenkt. Nach der
Flugstrecke l erreicht der Strahl den Fluoreszenzschirm (4), wo er als Lichtpunkt dargestellt wird. Dabei ist die Ablenkung y aus der Mitte des Schirms proportional zur Messspannung.
Moderne Oszilloskope haben zwischen dem Eingang und dem Ablenkkondensator
noch einen einstellbaren Verstärker, damit man Signale im Bereich von µV bis ca.
10V darstellen kann.
Heutige digitale Oszilloskope verwenden keinen Elektronenstrahl zur Darstellung. Viel
mehr wird die Eingangsspannung gemessen und digital auf einer LCD-Anzeige dargestellt.
Oszilloskop als Messgerät
Das Oszilloskop besitzt zwei zueinander senkrechte Ablenksysteme, die auf die zugeführte Spannung reagieren (simultane
Spannungsmessgeräte):
x- Richtung (horizontal) und
y- Richtung (vertikal) in der Bildschirm- Ebene.
Das Oszilloskop besitzt zwei Betriebsarten:
-
X- Y- Betriebsart: Kennlinien- Aufzeichnung;
-
X- T- Betriebsart: periodische Zeitsignal- Aufzeichung.
Schaltsymbol
Oszilloskop
Auf dem Bildschirm ist ein Gitternetz aus Skalenteilen ( Div ) aufgetragen, den zugehörige Messbereich zeigt der Messbereich- Umschalter (moderne Oszilloskope blenden den Messbereich oder den Skalenteil ein).
1
xy-Betriebsart
UCh1
UCh2
UCh1 wird auf der x-Achse, UCh2 auf der y-Achse dargestellt. Dabei hat jeder Eingang
eine eigene Skalenverstärkung kScale (Volt pro Skalenteil, V/DIV). Diese Betriebsart ist
u.A. geeignet zur Darstellung der Kennlinie von Bauteilen (Strom-SpannungsDiagramm).
xt-Betriebsart
UCh1, UCh2
In dieser Betriebsart wird an die horizontalen Ablenkplatten eine Sägezahnspannung
angelegt, das Messsignal wird an die vertikalen Ablenkplatten angelegt. Dadurch
erhält man ein Spannungs-Zeit-Diagramm der Eingangsspannung. Die Skalenverstärkungen sind kt in [ms/DIV oder µs/DIV] und kScale in [V/DIV]. Diese Betriebsart dient zur
Analyse des Eingangssignals (Zeitverzögerung, Sprungantwort, Signalverzerrung).
Darstellung von periodischen Signalen, Trigger
Um am Display ein ruhiges Bild des Messsignals zu erhalten, muss die Zeitablenkung
mit dem Signal synchronisiert werden. Dies geschieht durch den Wert der Triggerspannung UT: Steigt die Eingangsspannung über UT, so beginnt ein (horizontaler)
Durchlauf des Elektronenstrahls. Nach diesem Durchlauf „wartet“ das Oszilloskop ohne Bild, bis die Messspannung wieder UT überschreitet.
Tirgger-Einstellmöglichkeiten
Triggerspannung UT („Triggerlevel”)
Kanal: Soll auf Kanal 1 oder Kanal 2 „gehört“ werden (Ch1 oder Ch2)
-
Triggerflanke: aufsteigend oder absteigend (aufsteigend: Signal beginnt wenn
Messsignal von unten über UT ansteigt, absteigend: Signal beginnt, wenn Messsignal von oben unter UT abfällt)
2
2.
Funktionsgenerator
Grundlagen
Ein Funktionsgenerator ist eine einstellbare
Spannungsquelle, mit der unterschiedliche
Wechselspannungssignale erzeugt werden
können. Dabei sind folgende Einstellmöglichkeiten gegeben:
Signalform
Sinusform
Dreieckform
Rechteckform
Duty in %
Bei Rechteckform das Verhältnis
Bei Dreieckform das Verhältnis
Zeit wo Signal "1" ist
Zeit wo Signal "0" ist
Zeit der aufsteigenden Flanke
Zeit der absteigenden Flanke
Frequenz f
in [Hz]
Amplitude USS
USS = Umax . Umin (U Spitze-Spitze)
Offset
Spannung der Mittellinen, also UOffs =
1
(Umin + Umax )
2
3
3. RC-Tiefpass
3.1.
Sprungverhalten
Legt man an einen RC-Tiefpass eine rechteckige Wechselspannung so wird dieser
abwechselnd geladen und entladen.
I
0..10V
10V
R
R
R
UC
UC
C
UC
C
RC-Tiefpass
Ersatzschaltbild
Ladevorgang
C
Ersatzschaltbild
Entladevorgang
Entladevorgang
Anfänglich ist der Kondensator mit der Spannung U0 und der Ladung Q0 = C ⋅ U 0 geU
. Der
R
Strom ist gleich der negativen Änderung der Ladung (negativ, weil I aus dem KondU
dQ
densator gerechnet wird), also I = −
= −C ⋅
. Setzt man diese beiden Ausdrücke
dt
dt
für I gleich, so ergibt sich die Differentialgleichung für die Kondensatorspannung:
laden. Diese Spannung verursacht im Widerstand R einen Strom gemäß I =
dU
U
=−
dt
RC
Gl. 1
Lösung dieser Gleichung (z.B. mit dem Ansatz U = A ⋅ e −bt , A und b zu bestimmende
Konstanten) liefert die Funktion der Spannung:
U (t ) = U 0 ⋅ e
−
t
RC
Gl. 2
Das heißt, die Kondensatorspannung entlädt sich exponentiell.
Halbwertszeit
Die Halbwertszeit t1 2 ist definiert als die Zeit, bis die Spannung auf den halbe Wert
abgesunken ist, also U (t1 2 ) =
1
U 0 . Eingesetzt in Gl. 2 ergibt sich daraus
2
t1 2 = RC ⋅ ln(2)
3.2.
Gl. 3
Übertragungsfunktion und Phasenverschiebung
R
Ue
Ua
C
RC-Tiefpass
Schließt man den RC-Tiefpass an die Eingangsspannung U e = U Ch1 = u e sin (ω ⋅ t ) an, so
ergibt sich ein Zeitverzögertes Ausgangssignal U a = U Ch 2 = u a sin (ω ⋅ t − ϕ ) . Man defi-
niert:
4
Die Spannungsverstärkung Vu =
ua
und die Phasenverschiebung ϕ .
ue
Messung der Phasenverschiebung
∆t
Am Oszilloskop stellt sich die Phasenverschiebung nicht als Winkel (in Radiant oder
Grad) dar, sondern als Zeitverzögerung ∆t . Dabei entspricht eine Verzögerung von
∆t = T = 1 = 2π einem Winkel von 2π (360°). Daraus ergibt sich die Umrechnung für
f
ω
ϕ zu:
ϕ = 2π ⋅ f ⋅ ∆t = ω∆t
Gl. 4
Man kann also durch die Messung der Zeitverzögerung bei bekannter Frequenz die
Phasenverschiebung errechnen.
5
1.
Messung der Phssenverschiebung zweier Sinus-Signale
Grundlagen
Misst man mit einem Oszilloskop Eingangssignal und Ausgangssignal einer elektronischen AC-Schaltung, so besteht im allgemeinen eine Phasenverschiebung zwischen
diesen Signalen. In der XT-Betriebsart kann der Winkel der Phasenverschiebung gemessen werden.
Messung der Zeitverschiebung
∆t
U
t
T=1/f
Die Abbildung zeigt das XT-Diagramm für zwei Sinus-Signale mit Phasenverschiebung.
Am Oszilloskop kann man die zeitliche Verschiebung ∆t direkt ablesen: es ist dies die
Zeit zwischen zwei Nulldurchgängen (Zeit = Länge am Oszilloskop x Sec/Div). Ist das
Ausgangssignal nach links verschoben, so ist ∆t negativ, ansonsten positiv zu werten.
Berechnung des Phasenwinkels
Über eine Schlussrechnung kann man nun die Beziehung zwischen ∆t und ϕ erhalten:
Bei einer Verschiebung um die Zeit T (Periodendauer) wäre der Winkel 360°. Also gilt
für die Zeit ∆t:
ϕ = 360° ⋅
2.
∆t
= 360° ⋅ f ⋅ ∆t
T
Berechnung der komplexen Übertragungsfunktion
Grundlagen
Betrachtet man die elektrischen Messgrößen als Realteile der komplexen Funktionen
)
u = u 0 ⋅ e jωt
)
i = i 0 ⋅ e jωt
wobei u0, i0 die (komplexe) Amplitude der Messgröße und ω=2πf die Kreisfrequenz ist.
Dann kann man AC-Schaltungen ähnlich wie DC-Schaltungen berechnen, nur tritt
an die Stelle des ohmschen Widerstandes nun die (komplexe) Impedanz Z. Dabei
hat ein reiner Widerstand Z=R, ein reiner Kondensator Z=1/jωC und eine reine Spule
Z=jωL.
Berechnung der Übertragungsfunktion eines RC-Tiefpasses
Anhand des Beispiels eines RC-Tiefpasses soll die rechnerische Vorgehensweise demonstriert werden:
1
R
Ue
Ua
C
RC-Tiefpass
In dieser Schaltung ist nun Z1=R und Z2=1/jωC. Aus dem Ohmschen Gesetz ergibt sich
)
)
)
ue
ue
=
und damit die Spannung an Z2 zu
der Gesamtstrom i =
Z gesamt
Z1 + Z 2
Z2 )
u e (Spannungsteilerregel!).
Z1 + Z 2
)
Die komplexe Übertragungsfunktion Vu ist definiert als das Verhältnis von Ausgangs)
ua =
zu Eingangsspannung, also
)
)
ue
Z2
Vu = ) =
=
ua
Z1 + Z 2
1
jωC
1
=
1
1 + jωRC
R+
jωC
in diesem Beispiel. Erweitert man den Bruch mit dem konjugiert komplexen des Nenner so erhält man:
)
Vu =
1
1 − jωRC
1 − jωRC
⋅
=
1 + jωRC 1 − jωRC 1 + (ωRC)2
Zur Bestimmung der Verstärkung Vu (=Betrag der komplexen Übertragungsfunktion)
und der Phasenverschiebung ϕ geht man nun wie folgt vor:
(
)
2
Vu = Vu = 1 + (ωRC)
)
−1 2
 − ωRC

)
 Im(Vu ) 
 1 + (ωRC)2


ϕ = arctan
= arctan
)
 Re(V ) 
1
u 


 1 + (ωRC)2

2



 = arctan(−ωRC)


