Lösung zu Aufgabe 1 Merkmal Beispiele für Ausprägungen

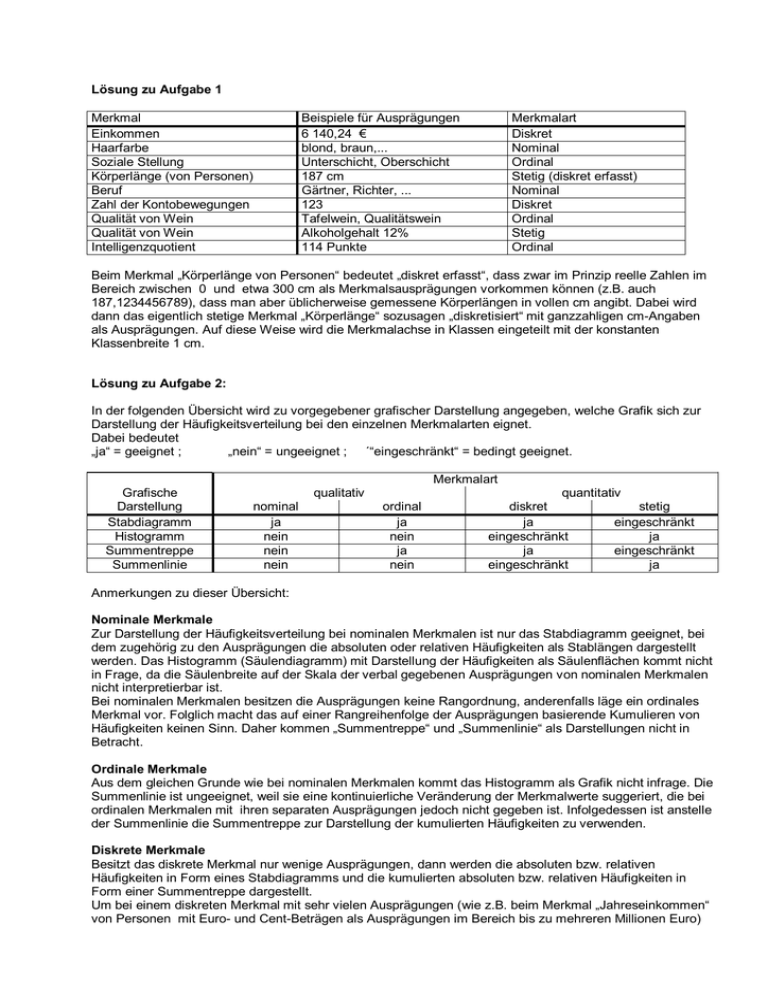
Lösung zu Aufgabe 1
Merkmal
Einkommen
Haarfarbe
Soziale Stellung
Körperlänge (von Personen)
Beruf
Zahl der Kontobewegungen
Qualität von Wein
Qualität von Wein
Intelligenzquotient
Beispiele für Ausprägungen
6 140,24 €
blond, braun,...
Unterschicht, Oberschicht
187 cm
Gärtner, Richter, ...
123
Tafelwein, Qualitätswein
Alkoholgehalt 12%
114 Punkte
Merkmalart
Diskret
Nominal
Ordinal
Stetig (diskret erfasst)
Nominal
Diskret
Ordinal
Stetig
Ordinal
Beim Merkmal „Körperlänge von Personen“ bedeutet „diskret erfasst“, dass zwar im Prinzip reelle Zahlen im
Bereich zwischen 0 und etwa 300 cm als Merkmalsausprägungen vorkommen können (z.B. auch
187,1234456789), dass man aber üblicherweise gemessene Körperlängen in vollen cm angibt. Dabei wird
dann das eigentlich stetige Merkmal „Körperlänge“ sozusagen „diskretisiert“ mit ganzzahligen cm-Angaben
als Ausprägungen. Auf diese Weise wird die Merkmalachse in Klassen eingeteilt mit der konstanten
Klassenbreite 1 cm.
Lösung zu Aufgabe 2:
In der folgenden Übersicht wird zu vorgegebener grafischer Darstellung angegeben, welche Grafik sich zur
Darstellung der Häufigkeitsverteilung bei den einzelnen Merkmalarten eignet.
Dabei bedeutet
„ja“ = geeignet ;
„nein“ = ungeeignet ; ´“eingeschränkt“ = bedingt geeignet.
Merkmalart
Grafische
Darstellung
Stabdiagramm
Histogramm
Summentreppe
Summenlinie
qualitativ
nominal
ja
nein
nein
nein
ordinal
ja
nein
ja
nein
quantitativ
diskret
stetig
ja
eingeschränkt
eingeschränkt
ja
ja
eingeschränkt
eingeschränkt
ja
Anmerkungen zu dieser Übersicht:
Nominale Merkmale
Zur Darstellung der Häufigkeitsverteilung bei nominalen Merkmalen ist nur das Stabdiagramm geeignet, bei
dem zugehörig zu den Ausprägungen die absoluten oder relativen Häufigkeiten als Stablängen dargestellt
werden. Das Histogramm (Säulendiagramm) mit Darstellung der Häufigkeiten als Säulenflächen kommt nicht
in Frage, da die Säulenbreite auf der Skala der verbal gegebenen Ausprägungen von nominalen Merkmalen
nicht interpretierbar ist.
Bei nominalen Merkmalen besitzen die Ausprägungen keine Rangordnung, anderenfalls läge ein ordinales
Merkmal vor. Folglich macht das auf einer Rangreihenfolge der Ausprägungen basierende Kumulieren von
Häufigkeiten keinen Sinn. Daher kommen „Summentreppe“ und „Summenlinie“ als Darstellungen nicht in
Betracht.
Ordinale Merkmale
Aus dem gleichen Grunde wie bei nominalen Merkmalen kommt das Histogramm als Grafik nicht infrage. Die
Summenlinie ist ungeeignet, weil sie eine kontinuierliche Veränderung der Merkmalwerte suggeriert, die bei
ordinalen Merkmalen mit ihren separaten Ausprägungen jedoch nicht gegeben ist. Infolgedessen ist anstelle
der Summenlinie die Summentreppe zur Darstellung der kumulierten Häufigkeiten zu verwenden.
Diskrete Merkmale
Besitzt das diskrete Merkmal nur wenige Ausprägungen, dann werden die absoluten bzw. relativen
Häufigkeiten in Form eines Stabdiagramms und die kumulierten absoluten bzw. relativen Häufigkeiten in
Form einer Summentreppe dargestellt.
Um bei einem diskreten Merkmal mit sehr vielen Ausprägungen (wie z.B. beim Merkmal „Jahreseinkommen“
von Personen mit Euro- und Cent-Beträgen als Ausprägungen im Bereich bis zu mehreren Millionen Euro)
eine übersichtliche grafische Darstellung zu erhalten, wird man die Ausprägungen geeignet zu Klassen
zusammenfassen. Unter dieser Einschränkung behandelt man dann das eigentlich diskrete Merkmal, wie
wenn es ein stetiges wäre: Dementsprechend werden dann die absoluten bzw. relativen Häufigkeiten
anhand eines Histogramms und die kumulierten absoluten bzw. relativen Häufigkeiten anhand einer
Summenlinie dargestellt.
Stetige Merkmale
Da bei stetigen Merkmalen im Prinzip alle reellen Zahlen innerhalb des Merkmalbereiches als Merkmalwerte
möglich sind, wird man für stetige Merkmale den Merkmalbereich i.a. in Intervalle (Klassen) einteilen. In
diesem Falle werden die absoluten bzw. relativen Häufigkeiten je Klasse in Form eines Säulendiagramms
(Histogramms) dargestellt, wobei die einzelnen Säulenflächen den zugehörigen Klassenhäufigkeiten
entsprechen.
Zugehörig dazu stellt man die kumulierten Häufigkeiten in Form einer Summenlinie (=Summenkurve) dar.
Es ist jedoch möglich ein stetiges Merkmal zu diskretisieren. So gibt man beispielsweise das Lebensalter
von Personen nicht exakt in Stunden (oder gar noch genauer in Minuten und Sekunden) an, sondern
üblicherweise in vollen Jahren. Dann ist das stetige Merkmal Lebensalter diskretisiert mit den ganzzahligen
Ausprägungen „Alter in Jahren“. Dabei hat man im Grunde genommen die Merkmalachse in Altersklassen
mit der konstanten Klassenbreite 1 Jahr eingeteilt.
Die Qualität von Wein läßt sich je nach Fragestellung verschiedenen Merkmalarten zuordnen. Aus der Sicht
eines Weinhändlers gibt es die ordinalen Ausprägungen Tafelwein, Qualitätswein, Prädikatswein. Ein
Kellermeister beurteilt die Qualität von Wein anhand von stetigen Merkmalen, wie z.B. Alkoholgehalt,
Säuregehalt, Zuckergehalt.
Lösung zu Aufgabe 3
Aus der gegebenen Klasseneinteilung (mit rechts abgeschlossenen Klassen) und zugehörigen
Klassenhäufigkeiten Ni erstellt man folgende Auswertungstabelle mit
Klassenbreiten bi , Klassenobergrenzen gi , kumulierten Häufigkeiten Ki :
Tab. 1
(1)
Kl. Nr. i
1
2
3
4
5
(2)
0 - 10
10 - 25
25 - 40
40 - 80
80 -
(3)
bi
10
15
15
40
−
(4)
gi
10
25
40
80
−
(5)
Ni
117
246
72
43
22
N=500
(6)
Ni / N
0,234
0,492
0,144
0,086
0,044
1,000
(7)
Ni / bi
11,70
16,40
4,80
1,08
−
(8)
(Ni/N) / bi
0,0234
0,0328
0,0096
0,0022
−
(9)
Ki
117
363
435
478
500
(10)
Ki / N
0,234
0,726
0,870
0,956
1,000
Zu (a)
Aus der Klasseneinteilung für das stetige Merkmal „Jahresfahrleistung“ erkennt man:
(1) Die einzelnen Klassen besitzen unterschiedliche Klassenbreiten bi , vgl. Spalte (3) von Tab. 1.
(2) Für die letzte Klasse läßt sich keine Klassenbreite angeben, da sie nach oben unbeschränkt ist.
Für stetige Merkmale wird die Häufigkeitsverteilung nicht in Form eines Stabdiagramms, sondern als
Säulendiagramm (Histogramm) dargestellt. Im Histogramm werden die absoluten Häufigkeiten Ni bzw. die
relativen Häufigkeiten Ni / N grafisch durch rechteckförmige Säulenflächen Fi = bi ⋅ hi mit Säulenbreite bi
und Säulenhöhe hi dargestellt. Aus der Forderung Fi = Ni bzw. Fi = Ni / N folgt, dass die Säulenhöhen
gemäß
N
N /N
bzw. hi = i
hi = i
bi
bi
zu bestimmen sind. Das Histogramm mit den Säulenhöhen hi = Ni / bi ist in Abb. 1 dargestellt.
Es zeigt nur die Säulen für die ersten 4 Klassen. Die Säule für Klasse 5 läßt sich nicht zeichnen, da die
Klassenbreite b5 nicht zur Verfügung steht, und daher die Säulenhöhe h5 nicht bestimmbar ist.
Abb. 1:
18
16
14
12
10
8
6
4
2
0
0
10
20
30
40
50
60
70
80
90
Der Wert von hi = Ni / bi besagt, wie viele Daten innerhalb einer Klasse durchschnittlich auf eine Einheit des
Merkmals „Entfernung“ ( hier : 1 000 km ) entfallen. Dabei wird unterstellt, dass sich die Daten einer Klasse
gleichmäßig über das Klassenintervall verteilen (ähnlich einer Flüssigkeit über dem Gefäßboden).
Beispielsweise bedeutet für Klasse Nr. 2 der Wert h2 = N2 / b2 = 246 / 15 = 16,4 , dass in Klasse 2
durchschnittlich 16,4 Daten auf ein Intervall der Breite 1 000 km entfallen, dass also im Mittel jeweils 16,4
Daten zwischen 10 000 und 11 000, zwischen 11 000 und 12 000 usw. liegen. Die Säulenhöhe hi ist
demnach ein Maß für die „Datendichte“ in Klasse i :
Je höher eine Säule, umso „dichter gedrängt“ liegen die Daten innerhalb der betreffenden Klasse.
Man bezeichnet daher hi = Ni / bi als absolute und hi = (Ni/N) / bi als relative Häufigkeitsdichte. Das
Histogramm (Säulendiagramm) der Abb. 1 zeigt, dass die Datendichte von der 1. zur 2. Klasse zunimmt, in
Klasse 2 am höchsten ist, und dann von Klasse zu Klasse abnimmt.
Bemerkung:
Je breiter eine Klasse ist, um so größer ist i.a. die Anzahl Ni der darin enthaltenen Daten. Ni hängt also u.a.
von der gewählten Klassenbreite bi ab, d.h. Ni = Ni(bi). Würde man Histogramme mit Ni als Säulenhöhen
zeichnen, dann würden zu verschiedenen Klasseneinteilungen gehörige Histogramme eines bestimmten
Datensatzes kaum Ähnlichkeit untereinander aufweisen. Um dies zu vermeiden, wählt man als Säulenhöhe
hi = Ni / bi und schaltet damit den Einfluss unterschiedlich gewählter Klasseneinteilungen auf die Gestalt
des Histogramms weitgehend aus.
Zu (b):
Für stetige Merkmale werden die kumulierten Häufigkeiten Ki anhand der sogenannten Summenlinie
(Summenkurve) dargestellt. Die kumulierte absolute Häufigkeit für Klasse i ist definiert als
Ki = N1 + N2 + ... + Ni ,
vgl. Spalte (9) von Tab. 1. Ki gibt an, wie viele Autofahrer eine jährliche Fahrtstrecke bis zur
Klassenobergrenze gi der Klasse i zurückgelegt haben. Laut Tab.1 sind zum Beispiel K2 = 117 + 246 = 363
Autofahrer bis zu 25 000 km im Jahr gefahren. Klassenobergrenzen gi und kumulierte Häufigkeiten Ki
gehören also stets paarweise zusammen. Die Zahlenpaare ( gi ; Ki ) trägt man als Punkte in ein
Koordinatensystem ein. Die Summenlinie ist dann der Polygonzug durch diese Punkte und stellt die
kumulierten Häufigkeiten grafisch dar, siehe Abb. 2.
Ersichtlich fehlt bei der Summenlinie in Abb. 2 die zu Klasse 5 gehörende Strecke. Diese läßt sich nicht
zeichnen; denn wegen der nach oben unbeschränkten Randklasse Nr. 5 fehlt für den letzten Punkt ( g5 ; K5 )
der Summenlinie die erforderliche Angabe der Klassenobergrenze g5 .
Abb 2:
500
450
400
350
300
250
200
150
100
50
0
0
10
20
30
40
50
60
70
80
90
Zu (c): Siehe Abb. 3
Abb. 3 zeigt die Summenlinie der relativen kumulierten Häufigkeiten Ki / N [%].
An der Summenlinie liest man (im Rahmen der Zeichengenauigkeit ausreichend genau) ab, dass etwa 90%
der Autofahrer bis zu 50 000 km und etwa 40% der Autofahrer bis zu 15 000 km zurückgelegt haben.
Demnach hatten 50% der Autofahrer eine Jahresfahrleistung zwischen 15 000 und 50 000 km.
Zu (d): Siehe Abb. 4
Man liest die gesuchte Jahresfahrleistung an der Summenlinie ab, indem man beim Wert 50% auf der
Ordinate eine Waagrechte bis zum Schnitt mit der Summenlinie zieht, und dann den Schnittpunkt auf die
Abszisse lotet. Dabei erhält man (im Rahmen der Zeichengenauigkeit ausreichend genau) den Wert 18 000
km, siehe Abb. 4. Diese Fahrtstrecke wird also von einer Hälfte der Autofahrer unter- und von der anderen
Hälfte überschritten und stellt somit eine sehr anschauliche mittlere Fahrleistung dar.
Abb. 3:
100
90
80
70
60
50
40
30
20
10
0
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
Abb. 4:
100
90
80
70
60
50
40
30
20
10
0
0
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
Lösung zu Aufgabe 4
Für das stetige Merkmal „Entfernung“ wird die Häufigkeitsverteilung grafisch durch ein Histogramm
(Säulendiagramm) dargestellt. Die Säulen sind rechteckförmig mit Säulenbreite = Klassenbreite bi ,
Säulenhöhe hi und Säulenfläche Fi = bi ⋅ hi . Im gegebenen Histogramm sind die absoluten Häufigkeiten Ni
für Klasse Nr. i geometrisch als Säulenflächen Fi dargestellt, so dass Ni = bi ⋅ hi gilt, siehe auch
nachstehende Tabelle.
(1)
Klasse
Nr. i
(2)
Entfernungsklasse
(3)
Klassenobergrenze gi
(4)
Klassenbreite bi
(5)
Säulenhöhe hi
1
2
3
0 − 10
10 – 30
30 − 70
10
30
70
10
20
40
30
25
5
(6)
(7)
Kumulierte
Absolute
absolute
Häufigkeit
Häufigkeit Ki
Ni = bi ⋅ hi
300
300
500
800
200
N =1000
N = 1000
Zum Betrieb gehören also N = Σ Ni = 1000 Beschäftigte.
Grafik A ist keine korrekte Darstellung der kumulierten absoluten Häufigkeiten Ki . Denn zum einen sind die
Ki für das stetige Merkmal „Entfernung“ nicht durch eine Summentreppe, sondern durch eine Summenlinie
darzustellen, zum anderen müssten die Ki bis zur Gesamtzahl N = 1000 der Beschäftigten ansteigen.
Die zu den Daten passende Darstellung der Summenlinie findet man, indem man die Ki über den in Spalte
(3) angegebenen Klassenobergrenzen gi abträgt und die eingetragenen Punkte ( gi ; Ki ) durch einen
Polygonzug verbindet, siehe Grafik C.
Grafik B ist nicht korrekt, weil dabei die Säulenhöhen hi des Histogramms fälschlicherweise als Häufigkeiten
interpretiert und kumuliert sind.
Grafik D ist nicht korrekt, weil die Ki - Werte aus Spalte (7) statt über den Klassenobergrenzen
fälschlicherweise über den Klassenmitten abgetragen sind.
Lösung zu Aufgabe 5:
Bei dem abgebildeten Säulendiagramm (Histogramm) ist auf der senkrechten Achse die absolute
Häufigkeitsdichte abgetragen. Das ist die absolute Häufigkeit, die jeweils innerhalb einer Klasse
durchschnittlich auf ein Intervall der Länge einer Einheit des Merkmals (hier 100.000 Euro) entfällt. So
bedeutet beispielsweise die Säulenhöhe 50 der Klasse von 300.000 bis 700.000 Euro, dass in dieser Klasse
im Schnitt jeweils 50 Filialen auf ein Umsatzintervall der Breite 100.000 Euro entfallen, also z.B. 50 Filialen
auf das Intervall zwischen 300.000 und 400.000 bzw. zwischen 400.000 und 500.000 usw. oder z.B. 50
Filialen auf das Intervall zwischen 350.000 und 450.000 Euro.
Dementsprechend erhält man durch Multiplikation der Klassenbreite ( =Säulenbreite ) bi mit der Säulenhöhe
hi = Ni / bi die Anzahl Ni der Filialen in Klasse i. Die absolute Häufigkeit Ni ist also geometrisch als
Säulenfläche bi ⋅ hi dargestellt.
Für die vier Umsatzklassen ermittelt man auf diese Weise folgende Häufigkeitstabelle:
Klasse Nr. i
Säulenhöhe hi
Säulenbreite bi [100.000 Euro]
absolute Häufigkeit Ni = bi ⋅ hi
relative Häufigkeit Ni / N
1
200
1
200
0,25
2
100
2
200
0,25
3
50
4
200
0,25
4
25
8
200
0,25
Summe
800 = N
1,00
Wie die Tabelle zeigt, haben alle Klassenhäufigkeiten Ni den gleichen Wert 200 und damit die relativen
Häufigkeiten Ni / N den Wert 200 / 800 = 0,25.
Folglich ist Aussage A und damit auch Aussage B falsch.
Da jede Umsatzklasse die gleiche Anzahl von Filialen enthält, die Klassen aber zu größeren Umsätzen hin
breiter werden, nimmt dementsprechend die Datendichte innerhalb der Klassen und damit die Säulenhöhe
hi ab. Aussage C ist also richtig.
Der Umsatz einer Filiale aus einer bestimmten Umsatzklasse ist stets kleiner als der Umsatz einer Filiale aus
einer rechts daneben liegenden Umsatzklasse mit höheren Umsatzwerten. Folglich ist auch der
Gesamtumsatz der 200 Filialen einer Klasse um so höher, je weiter rechts die Klasse auf der Umsatzskala
liegt. Damit nimmt auch der Anteil einer Umsatzklasse am Gesamtumsatz zusammen mit dem
Monatsumsatz zu. Demnach ist Aussage D richtig.
Über die Verteilung des Gesamtumsatzes einer bestimmten Umsatzklasse auf die Filialen der Klasse ist
nichts bekannt. Möglicherweise setzen alle 200 Filialen der ersten Klasse jeweils 50.000 Euro um, so dass
sich innerhalb der ersten Klasse der Gesamtumsatz gleichmäßig auf alle Filialen aufteilt, dagegen könnten
von den 200 Filialen der vierten Klasse jeweils 100 Filialen 800.000 Euro und 100 Filialen 1.500.000 Euro
umsetzen, so dass innerhalb dieser Klasse keine Gleichverteilung des Umsatzes auf die Filialen, sondern
Konzentration besteht. Bei der beschriebenen Situation ist dann der Umsatz innerhalb der vierten Klasse
ungleichmäßiger verteilt als innerhalb der ersten Klasse. Daher ist Aussage E falsch.
Beim Gruppieren von Daten in Klassen geht die Information darüber verloren, wie sich die Daten innen einer
Klasse verteilen. Über die tatsächliche Verteilung der Umsatzdaten über dem Wertebereich innerhalb einer
Umsatzklasse lassen sich demnach aus dem Histogramm keine Informationen entnehmen.
Folglich läßt sich auch über die Gleichmäßigkeit der Umsatzverteilung innerhalb der einzelnen
Umsatzklassen nichts aussagen. Also ist Aussage F falsch.
Bemerkung:
Beim Zeichnen eines Histogramms wird die verlorene Information ersetzt durch die meist auf die Realität
nicht oder allenfalls nur näherungsweise zutreffende Annahme, dass sich die Daten innerhalb der Klasse
gleichmäßig über den Wertebereich verteilen. Dies wird im Histogramm grafisch dargestellt durch den
waagrechten „Datenpegelstand“ am oberen Ende der Säulen.
Lösung zu Aufgabe 6
(a) Aus den gegebenen Daten für die N = 500 000 Arbeitsstätten mit insgesamt
B = 2 500 000 Beschäftigten erstellt man folgende Arbeitstabelle:
Tab. 1:
(1)
Arbeitsstätte
Klasse mit … bis…
Nr. i
Beschäftigten
1
1–2
2
3–5
3
6–9
4
10 – 19
5
20 –
Σ
(2)
(3)
(4)
(5)
Arbeitsstätten
Ni [Tsd.] Ni/N [%] Ki/N [%] Bi [Tsd.]
230
46
46
350
160
32
78
600
70
14
92
490
30
6
98
430
10
2
100
630
N = 500
100
− B = 2 500
(6)
(7)
Betriebe
Bi / B [%] kum. Bi / B [%]
14,0
14,0
24,0
38,0
19,6
57,6
17,2
74,8
25,2
100,0
100,0
−
Zur Lorenzkurve kommt man, indem man die Zahlenpaare ( Ki / N ; kum. Bi / B ), ergänzt um das
Zahlenpaar ( 0 ; 0 ) , in ein Koordinatensystem einträgt und die Punkte durch einen Polygonzug verbindet,
siehe Abb. 1.
Bei der Verbindung der Punkte durch Strecken wird unterstellt, dass sich die Gesamtzahl der Beschäftigten
einer Klasse jeweils gleichmäßig auf die Ausprägungen innerhalb dieser Klasse aufteilt. So wird z.B. für
Klasse Nr. 2 angenommen, dass von den insgesamt 600 000 Beschäftigten dieser Klasse jeweils 200 000
auf die drei zu dieser Klasse gehörenden Ausprägungen 3 bzw. 4 bzw. 5 entfallen.
Abb. 1:
100
90
80
Beschäftigte
70
60
50
40
30
20
10
0
0
10
20
30
40
50
60
70
80
90 100
Arbeitsstätten
( b ) Unter der in (a) gemachten Annahme und im Rahmen der Zeichengenauigkeit liest man - ausgehend
von dem auf der Achse der Arbeitsstätten vorgegebenen Wert 50% - an der Lorenzkurve den
Näherungswert 17% für den gesuchten Beschäftigtenanteil ab, siehe die strichpunktierte Linie in Abb. 2 ,
( c ) Unter der in (a) gemachten Annahme und im Rahmen der Zeichengenauigkeit liest man - ausgehend
von dem auf der Achse der Beschäftigten vorgegebenen Wert 50% - an der Lorenzkurve zunächst den
Näherungswert 87% ab, siehe die gestrichelte Linie in Abb. 2. Dieser Wert 87% ist jedoch nicht der
gesuchte Anteil, sondern der Anteil der kleinsten Arbeitsstätten, in denen 50% der Beschäftigten tätig sind.
Folglich ist 100% − 87% = 13% der gesuchte Anteil der größten Arbeitsstätten mit 50% der Beschäftigten.
( d ) Der Zentralwert (Median) ist die Ausprägung, die von höchstens 50% der Daten unterschritten und von
höchstens 50% der Daten überschritten wird. Aus Spalte (2) bzw. (3) bzw. (4) von Tab. 1 geht hervor, dass
sich der Zentralwert in der Klasse Nr. 2 befindet. Unter der Annahme, dass sich die Häufigkeiten jeweils
gleichmäßig auf die Ausprägungen einer Klasse verteilen, entfallen von den 160 000 Arbeitsstätten in Klasse
Nr. 2 jeweils etwa 53 000 auf die drei Ausprägungen 3 bzw. 4 bzw. 5. Hieraus folgt dann für den Median
der Wert 3 . Denn 230 000 Arbeitsstätten, das ist weniger als die Hälfte, haben weniger als 3 Beschäftigte.
Etwa 230 000 + 53 000 = 283 000 Arbeitsstätten haben bis zu 3 Beschäftigte, so dass etwa 217 000
Arbeitsstätten, also ebenfalls weniger als die Hälfte, mehr als 3 Beschäftigte haben.
Obwohl die letzte Klasse nach oben unbeschränkt ist, läßt sich hier das arithmetische Mittel µ bestimmen,.
und zwar anhand der Definition des arithmetischen Mittels als Quotient B / N aus dem gegebenen
Gesamtmerkmalsbetrag B = 2 500 000 und der Zahl N = 500 000 der Merkmalsträger. Demnach ergibt sich
hier µ = B / N = 2 500 000 / 500 000 = 5. Es sind also im Mittel 5 Beschäftigte je Arbeitsstätte tätig.
Abb. 2:
100
90
80
Beschäftigte
70
60
50
40
30
20
10
0
0
10
20
30
40
50
60
70
80
90
100
Arbeitsstätten
Lösung zu Aufgabe 7
Zu (a) :
Die kumulierten Häufigkeiten Ki geben jeweils an, wie viel Betriebe eine Fläche von höchstens xi Hektar
bewirtschaften. Daher sind die in der Aufgabenstellung gegebenen Betriebsflächenwerte vor dem
Kumulieren aufsteigend anzuordnen und die zugehörigen absoluten Häufigkeiten entsprechend
umzuordnen, vgl. die beiden ersten Zeilen von Tab. 1.
Tab. 1:
Zeile
1
2
3
4
5
6
7
Nr. i
xi [ha]
Ni
Ki
Ki / N
Bi = Ni ⋅ xi
Bi / B
kum. Bi / B
1
2
3
4
5
20
30
50
100 200
Σ
5
5
7
2
1
N = 20
5
10
17
19
20
⎯
0,25 0,50 0,85 0,95 1,00
⎯
100 150 350 200 200 B = 1000
0,10 0,15 0,35 0,20 0,20
1,00
0,10 0,25 0,60 0,80 1,00
⎯
Ni Betriebe mit jeweils xi [ha] Betriebsfläche bewirtschaften zusammen Bi = Ni ⋅ xi [ha], vgl. Tab. 1, Zeile 5.
Die Gesamtbetriebsfläche B der 20 Betriebe ist daher B = Σ Bi = Σ Ni xi = 1 000 ha .
Aus den Bi -Werten findet man die Flächenanteile Bi / B und daraus die kumulierten ( Bi / B ) - Werte in Zeile
7 von Tab. 1. Der Polygonzug der Lorenzkurve ist dann bestimmt durch die Punkte ( Ki / N ; kum. Bi / B),
ergänzt um den Punkt ( 0 ; 0 ) , siehe Abb. 1.
Kumulierte Flächenanteile
Abb. 1
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Kumulierte Häufigkeiten der Betriebe
Zu (b):
1. Die 5 größten Betriebe bewirtschaften zusammen 200 + 100 + 100 + 50 + 50 = 500 ha und damit
50% der Landfläche von 1000 ha. Dies ist eine Aussage zur absoluten Konzentration, da ein
relativer Merkmalsbetrag (hier: Betriebsflächenanteil ) auf eine absolute Häufigkeit von Betrieben,
nämlich die 5 größten, bezogen wird.
2. Bei 20 Betrieben stellt ein einzelner 5% der Betriebe dar. Die 5% größten Betriebe bestehen also
hier allein aus dem größten Betrieb mit 200 ha bzw. 20% der Landfläche. Dies ist eine Aussage
zur relativen Konzentration, da der Betriebsflächenanteil 20% auf eine relative Häufigkeit von
Betrieben, nämlich die 5% größten, bezogen wird.
Lösung zu Aufgabe 8:
Trägt man die drei gegebenen Punkte ( 0 ; 0 ) , (1 ; 0 ) und ( 1; 1 ) in ein Koordinatensystem ein und
verbindet sie durch einen Polygonzug, so erhält man die nachstehend abgebildete Lorenzkurve:
kumulierte Gewinnanteile
1
Reihe1
Reihe2
0,5
0
0
0,5
1
kumulierte Anteile der Spieler
Es bezeichne N die Anzahl der Spieler, Ki / N die kumulierten Anteile der Spieler, B den Gesamtgewinn und
kum Bi / B die kumulierten Gewinnanteile.
Der GINI-Koeffizient G ist das Doppelte der Fläche zwischen der Gleichverteilungslinie (im Bild gestrichelt)
und der Lorenzkurve (fette Linie im Bild), also das Doppelte der Fläche des Dreiecks mit den Ecken ( 0 ; 0 ) ;
( 0,5 ; 0 ) und ( 1 ; 1 ) . Dieses Dreieck hat den Flächeninhalt 0,25. Somit gilt G = 2 ⋅ 0,25 = 0,50, so dass
Aussage A falsch und Aussage B richtig ist.
Die waagrechte Strecke der Lorenzkurve von ( 0 ; 0 ) bis ( 0,5 ; 0 ) bedeutet, dass 50% der Mitspieler keinen
Anteil an der Gewinnsumme haben, also beim Spiel leer ausgehen, also ist Aussage C richtig.
Die Strecke der Lorenzkurve von ( 0,5 ; 0 ) bis ( 1 ; 1 ) bedeutet, dass sich die gesamte Gewinnsumme auf
50% Mitspieler (die Gewinner) gleichmäßig aufteilt. Daher ist Aussage D richtig.
Gewänne ein Spieler die Hälfte des Gesamtgewinns, so müssten (weil sich nach Aussage D der Gewinn
gleichmäßig auf die Gewinner verteilt) alle Spieler, die überhaupt etwas gewinnen, jeweils die Hälfte des
Gesamtgewinns erhalten. Folglich müsste es genau zwei Gewinner geben und somit (weil sich nach
Aussage C die Hälfte der Spieler nichts gewinnt und nach Aussage D die andre Hälfte alles) insgesamt
genau vier Mitspieler. Dies ist nicht vorausgesetzt. Daher ist Aussage E nicht (allgemein) richtig.
Wäre Aussage F richtig, so müsste jeder Spieler etwas gewinnen, was der als richtig erkannten Aussage C
widerspräche. Daher ist Aussage F falsch.
Lösung zu Aufgabe 9:
Zu a)
Da jeder der 60 Kleinbetriebe mit 0,1% am Gesamtumsatz beteiligt ist, entfallen auf sie insgesamt 6% des
Gesamtumsatzes. Entsprechend sind die 30 Mittelbetriebe mit 30 ⋅ 0,8% = 24% und die 10 Großbetriebe mit
10 ⋅ 7% = 70% am Gesamtumsatz beteiligt.
Diese Angaben sind in Tab a übersichtlich zusammengestellt.
Tab. a:
Häufigkeiten der Betriebe
relativ
kumuliert
absolut
in %
in %
60
60
60
30
30
90
10
10
100
100
100
⎯
Betriebsgrößenklasse
Kleinbetriebe
Mittelbetriebe
Großbetriebe
insgesamt
Umsatzanteile
kumuliert
in %
in %
6
6
24
30
70
100
100
⎯
Aus den kumulierten relativen Häufigkeiten und den kumulierten Umsatzanteilen ergibt sich die Lorenzkurve
in Abb. 1:
Abb. 1
1
kumulierte Umsatzanteile
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
kumulierte Häufigkeit der Betriebe
Zu b)
Die angegebenen Veränderungen führen zu Tab. b der Umsatzverteilung auf die Betriebe:
Tab. b:
Betriebsgrössenklasse
Mittelbetriebe
Großbetriebe
insgesamt
Häufigkeiten der Betriebe
relativ
kumuliert
absolut
in %
in %
30
75
75
10
25
100
10
100
⎯
Umsatzanteile
kumuliert
in %
in %
30
30
70
100
100
⎯
Aus den kumulierten relativen Häufigkeiten und den kumulierten Umsatzanteilen von Tab. b resultiert die
Lorenzkurve der Abb. 2.
Abb. 2
1,0
kumulierte Umsatzsanteile
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,0
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
kumulierte Häufigkeit der Betriebe
Zu (c)
Der Vergleich von Abb. 1 mit Abb. 2 zeigt: In Abb. 2 liegt die Lorenzkurve näher bei der Gleichverteilungslinie als in Abb. 1. Daher ist die relative Konzentration der Umsätze auf die Betriebe im Fall b) geringer als im
Fall a). Dies ist auch ökonomisch einsichtig: Denn der Gesamtumsatz verteilt sich im Fall b) auf die (noch
vorhandenen 40) Betriebe gleichmäßiger als im Fall a), weil das Ausscheiden der Kleinbetriebe und die
Übernahme ihrer Umsatzanteile durch die Mittelbetriebe die Umsatzunterschiede zwischen den
verbleibenden Betrieben verringert hat; infolge dessen liegt die Lorenzkurve näher bei der
Gleichverteilungslinie als im Fall a).
Zu (d)
Gemessen an den 10 umsatzstärksten Betrieben hat sich die absolute Konzentration nicht erhöht: Denn wie
der Vergleich von Tabelle 1 mit Tabelle 2 zeigt, haben die 10 umsatzstärksten Betriebe in den beiden Fällen
a) und b) jeweils 70% Umsatzanteil.
Gemessen an den 15 umsatzstärksten Betrieben hat sich die absolute Konzentration jedoch erhöht. Denn im
Fall a) haben die 15 umsatzstärksten Betriebe zusammen den Umsatzanteil 10 ⋅ 7 % + 5 ⋅ 0,8% = 74% ,
im Fall b) jedoch den Umsatzanteil 10 ⋅ 7 % + 5 ⋅ 1,0 % = 75% . Der Umsatzanteil der 15 umsatzstärksten
Betriebe ist also im Fall b) größer als im Fall a).
Die absolute Konzentration, gemessen an den 15 größten Betrieben ist also durch die Schließung der
Kleinbetriebe und die dadurch verringerte Anzahl der Betriebe gestiegen.
Das Beispiel zeigt, dass die relative Konzentration abnehmen kann, obwohl gleichzeitig die absolute
Konzentration zunimmt.
Lösung zu Aufgabe 10
Zu (a):
Aus den Werten N i bzw. Ai im Aufgabentext erstellt man Tab. 1.
Tab. 1:
Kl. Kl.-einNr. i teilung
1
2
3
4
5
6
0 - 10
10 - 20
20 - 50
50 -100
100-200
200-600
Kl. oberKl.-breite grenze
gi
bi
10
10
10
20
30
50
50
100
100
200
400
600
Ni
Ki =
N1 +...+ N i
Ki / N
Ai
2 400
2 900
2 100
1 500
800
300
10 000
2 400
5 300
7 400
8 900
9 700
10 000
0,24
0,53
0,74
0,89
0,97
1,00
10
50
100
120
120
100
A =500
Bi =
A1 +...+ Ai
10
60
160
280
400
500
Bi / A
0,02
0,12
0,32
0,56
0,80
1,00
Zeichnet man in ein rechtwinkliges Koordinatensystem die Punkte ( gi ; K i / N ) bzw. ( gi ; B i / A) und
verbindet diese Punkte durch einen Streckenzug, so erhält man die beiden gesuchten Summenkurven der
Abb.1 (durchgezogene Linie: Summenlinie der relativen Häufigkeiten, gestrichelte Linie: Summenlinie der
Auftragswertanteile)
kumulierte rel. Häufigkeiten
bzw. kumulierte Umsatzanteile
Abb.1
1,00
0,95
0,90
0,85
0,80
0,75
0,70
0,65
0,60
0,55
0,50
0,45
0,40
0,35
0,30
0,25
0,20
0,15
0,10
0,05
0,00
0
100
200
300
400
500
600
Rechnungsbetrag
Zu (c) :
Der Anteil der Rechnungen mit einem Mindestwert von 75 € lässt sich nur näherungsweise bestimmen, da
die exakte Verteilung der Rechnungsbeträge innerhalb der Klassen unbekannt ist. Dem in Abb. 1
durchgezogenen Streckenzug für die kumulierten Häufigkeiten K i / N liegt die Annahme zugrunde, dass
sich die Rechnungsbeträge innerhalb der Klassen gleichmäßig verteilen. Für den Anteil der Rechnungen mit
Wert bis zu 75 € liest man 0,815 =ˆ 81,5% ab. Der gesuchte Anteil der Rechnungen mit Mindestwert 75 €
ist dann 100% − 81,5% = 18,5%.
Zu (d):
Unter der Annahme, dass sich die Umsatzanteile jeweils gleichmäßig über das zugehörige Klassenintervall
verteilen, erhält man den in Abb. 1 gestrichelten Streckenzug. An diesem liest man ab, dass 44% des
Gesamtumsatzes auf Rechnungen bis zu 75 € entfallen. Also entfallen 56% des Gesamtumsatzes auf
Rechnungen über 75 €.
Zu (b):
Die Lorenzkurve erhält man, indem man die Werte K i / N und B i / A aus Tab. 1 paarweise in ein
rechtwinkliges Koordinatensystem einträgt und benachbarte Punkte durch Strecken verbindet, vgl. Abb. 2.
Anders als bei b) und c) wird hier bei der Verbindung der Punkte durch Strecken unterstellt, dass jeweils
alle Rechnungen innerhalb einer Klasse denselben („mittleren“) Rechnungsbetrag besitzen.
Abb.2
1
0,9
kumulierte Umsatzanteile
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
1
kumulierte relative Häufigkeiten der Aufträge
Zu (e):
Aus Abb. 2 liest man längs der gestrichelten Linie ab, dass auf die 90% kleinsten Rechnungsbeträge (siehe
Skala auf der Abszisse ) 59% des Gesamtumsatzes (abzulesen auf der Ordinate) entfällt.
Zu (f):
Aus Abb. 2 liest man längs der punktierten Linie ab, dass die Hälfte des Gesamtumsatzes auf die 85%
kleinsten Rechnungsbeträge, die andere Hälfte auf die 15% größten Rechnungsbeträge entfällt.
Zu (g):
Der Gini-Koeffizient ist definitionsgemäß der doppelte Inhalt der Fläche zwischen Lorenzkurve und
Gleichverteilungsgerade. Nach Annahme verläuft die Lorenzkurve des Folgejahres durch den Punkt P in
Abb. 3. Daraus kann zwar nicht geschlossen werden, dass die Lorenzkurve des Folgejahres ganz unterhalb
der gezeichneten Lorenzkurve verläuft. Da aber die Steigung einer Lorenzkurve nicht abnehmen kann,
verläuft die Lorenzkurve für das Folgejahr nicht oberhalb des in Abb. 2 gestrichelten Streckenzuges, der die
drei Punkte (0 ; 0) , P und (1 ; 1) verbindet. Damit ist aber klar, dass die Fläche, welche die Lorenzkurve
des Folgejahres mit der Gleichverteilungsgeraden einschließt, größer ist als die Fläche F in Abb. 3 . Der
Gini-Koeffizient wird also größer.
Abb. 3:
1
0,9
kumulierte Umsatzanteile
0,8
0,7
0,6
0,5
0,4
0,3
P
0,2
0,1
0
0
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
relative kumulierte Häufigkeiten
1
Lösung zu Aufgabe 11:
Zu (a):
Sortiert man die angegebenen Urlistenwerte xi , i = 1,...,50 , für das Merkmal „Semesterzahl“ nach den
auftretenden Ausprägungen zj = 1, ... , 6, so erhält man folgende Häufigkeitstabelle, in der zugehörig zu den
Ausprägungen zj die absoluten Häufigkeiten Nj und die kumulierten absoluten Häufigkeiten Kj eingetragen
sind:
(1)
Semesterzahl
zj
1
2
3
4
5
6
Summe
(2)
absolute Häufigkeit
Nj
10
12
18
6
2
2
N = 50
(3)
kumulierte absolute
Häufigkeit Kj
10
22
40
46
48
50 = N
−
(4)
Merkmalsbetrag
zj ⋅ Nj
10
24
54
24
10
12
B = 134
In der Tabelle bedeutet N die Gesamtzahl der Studierenden und die Summe B von Spalte (4) den
Gesamtmerkmalsbetrag, d.h. die Gesamtsumme der Semesterzahlen für die 50 Studierenden.
Die Summe B wird zur Berechnung des arithmetischen Mittels benötigt.
Die absoluten Häufigkeiten Ni aus Spalte (2) der obigen Tabelle sind in Abb. 1 in Form eines
Stabdiagramms, die kumulierten absoluten Häufigkeiten Ki aus Spalte (3) sind in Abb. 2 in Form einer
Summentreppe dargestellt.
Abb 1: Stabdiagramm
20
18
absolute Häufigkeit
16
14
12
10
8
6
4
2
0
1
2
3
4
Semesterzahl
5
6
kumulierte absolute Häufigkeit
Abb. 2 : Summentreppe
55
50
45
40
35
30
25
20
15
10
5
0
0
1
2
3
4
5
6
7
8
Semesterzahl
Zu (b): Da das Merkmal Semesterzahl metrisch ist, sind im Prinzip alle Mittelwerte bestimmbar, jedoch nicht
alle sinnvoll.
Arithmetisches Mittel µ
Das arithmetische Mittel µ errechnet sich zu
µ=
B 1 6
134
= ∑ z j ⋅ Nj =
= 2,68 .
N N j=1
50
Man kann µ auch mit Hilfe der 50 gegebenen Urlistenwerte x1 = 4 ; x2 = 5 ; ...; x50 = 3 berechnen:
µ=
1 N
1
134
xi =
(4 + 5 + ... + 3) =
= 2,68
∑
N i=1
50
50
Zentralwert (Median) Z:
Lösungsweg 1:
Laut Definition ist der Zentralwert die Ausprägung, die von höchstens 50% der Daten (Urlistenwerte)
unterschritten und von höchstens 50% der Daten überschritten wird.
Anhand dieser Definition läßt sich für den Zentralwert Z direkt aus der Häufigkeitstabelle der Wert Z = 3
ablesen: Denn bei 22 von den 50 Urlistenwerten, also bei weniger als 50% der Studierenden ist die
Semesterzahl kleiner als 3 und bei 10 von den 50 Urlistenwerten, also bei weniger als 50% ist die
Semesterzahl größer als 3. Somit erfüllt die Semesterzahl 3 die Definition des Medians.
Lösungsweg 2:
Da das Merkmal Semesterzahl metrisch ist, kann man den Median aber auch anhand der nach der Größe
geordneten Werte x(i) mit der für gerade Datenanzahl N geltenden Formel
Z = [ x(N/2) + x(N/2+1) ] / 2
berechnen, d.h. der Median ist die Mitte zwischen den beiden der Größe nach mittleren Beobachtungen x(N/2)
und x(N/2+1) .
Demnach hat man speziell für N = 50:
Z = [ x(25) + x(26) ] / 2 .
Aus der Häufigkeitstabelle entnimmt man, dass die 22 kleinsten Urlistenwerte die Semesterzahlen 1 und 2
sind, und dass die nächsten 18 Werte, also die 23.-größte x(23) bis zur 40.-größten x(40) jeweils den Wert 3
besitzen. Somit ist x(25) = 3 und x(26) = 3 woraus sich nach der obigen Formel für den Zentralwert
Z=[3+3]/2=3
ergibt.
Lösungsweg 3:
Geht man in Abb. 2 auf der Skala der kumulierten absoluten Häufigkeit 25 (das entspricht der relativen
Häufigkeit 50%) waagrecht nach rechts bis zum Schnitt mit der Summentreppe, und lotet den Schnittpunkt
nach unten so liest man an der waagrechten Merkmalsachse für den Median den Wert Z = 3 ab.
Modalwert M
Man ersieht direkt aus der Häufigkeitstabelle oder aus Abb. 1, dass 3 die am häufigsten auftretende
Semesterzahl ist. Also ist 3 der Modalwert.
Geometrischer Mittelwert Mg
Im Gegensatz zur Summe x1 + ... + x50 der Daten läßt sich das Produkt x1 ⋅ ... ⋅ x50 der Daten im
vorliegenden Sachkontext inhaltlich nicht interpretieren. Daher ist das geometrische Mittel (obwohl es sich im
vorliegenden Fall rein formal bilden ließe) kein geeignetes Lagemaß.
Lösung zu Aufgabe 12:
Aus der Aufgabenstellung geht nicht hervor, auf welche Art von Merkmal sich diese Urliste bezieht.
Es könnte ein metrisches Merkmal sein, wie z.B. Temperaturen, gemessen in Grad Celsius oder ein
ordinales, wie z.B. auf einer Sympathieskala von –7 ( =“sehr unsympathisch“ ) bis +7 (= „sehr sympathisch“)
oder ein nominales Merkmal mit den etwas eigenwilligen abkürzenden Symbolen –7 bis +6 für die
verbalen Ausprägungen.
Daher sind bei der Beantwortung der gestellten Fragen diese drei Möglichkeiten zu betrachten. Es ergibt
sich folgende Übersicht:
Kenngröße
Arithmetisches Mittel µ
Modalwert
( = häufigster Wert) M
Median (Zentralwert) Z
Geometrisches Mittel Mg
Variationskoeffizient v
Merkmalart
metrisch
ja ( µ = 0 )
nein
ordinal
nein
nein
nominal
nein
nein
ja ( Z = 2)
nein
nein
ja (Z = 2 )
nein
nein
nein
nein
nein
In der Übersicht bedeutet für die betreffende Kenngröße
„ja“,
dass sie bestimmbar ist,
„nein“, dass sie nicht bestimmbar ist.
Arithmetisches Mittel µ
Da sich die Merkmalwerte nur für metrische Merkmale numerisch addieren lassen, läßt sich der
arithmetische Mittelwert nur für metrische Merkmale nicht jedoch für nominale oder ordinale Merkmale
bestimmen. Falls das vorliegende Merkmal metrisch ist erhält man hier den Wert µ = 0.
Modalwert M
Da jeder Merkmalwert in der obigen Urliste genau einmal notiert ist, gibt es – unabhängig von der
Merkmalart – keinen häufigsten Wert.
Zentralwert Z
Die Bestimmung des Zentralwerts erfordert, dass sich die möglichen Merkmalwerte in eine (bezüglich der
Fragestellung) natürliche Reihenfolge anordnen lassen. Dies ist bei metrischen und ordinalen Merkmalen
möglich, jedoch nicht bei nominalen Merkmalen; denn für diese stehen alle Merkmalwerte gleichberechtigt
nebeneinander.
Falls die obigen Daten für ein metrisches Merkmal (wie z.B. Temperatur) bzw. für ein ordinales Merkmal
(wie z.B. Sympathiewerte) ermittelt wurden und falls sie bereits in der natürlichen Reihenfolge aufgelistet
sind, ist der Zentralwert Z der mittlere von den sieben Werten, also der 4.-größte. Demnach ist hier Z = 2.
Geometrisches Mittel Mg
Da zur Bestimmung des geometrischen Mittels Mg
arithmetische Operationen (Multiplikation und
Wurzelziehen) durchzuführen sind, läßt sich das geometrische Mittel bei nominalen und ordinalen Daten
generell nicht bestimmen. Damit sich Mg bei metrischen Merkmalen stets berechnen läßt, ist zu fordern, dass
alle Merkmalwerte positives Vorzeichen besitzen. Bei den obigen Daten treten negative Werte auf, daher ist
das geometrische Mittel nicht bestimmbar.
Bemerkung: In den Anwendungssituationen, in denen der geometrische Mittelwert das geeignete Lagemaß
darstellt, tritt der Fall negativer Merkmalwerte nicht auf.
Variationskoeffizient v = µ / σ
Zur Bestimmung des Variationskoeffizienten v = µ /σ ist das arithmetische Mittel µ und die
Standardabweichung σ zu ermitteln, was bei nominalen und ordinalen Merkmalen nicht möglich ist.
Stammen die aufgelisteten Daten von einem metrischen Merkmal, kann man sowohl den Mittelwert µ = 0 als
auch die Standardabweichung σ = 22 = 4,69 ermitteln. Der Variationskoeffizent ist hier jedoch nicht
bestimmbar, da der Quotient σ / µ für µ = 0 nicht definiert ist.
Lösung zu Aufgabe 13
Zur Berechnung der mittleren Schadenhöhe hat man die Gesamtschadenssumme S = 3,500 Mrd. Euro
durch den Umfang N der jeweils betrachteten Grundgesamtheit zu dividieren.
Zu (a):
Die Grundgesamtheit der Verträge hat den Umfang Na = Σ Nj = 2 Mio. (vgl. Summe der Spalte (3) in
nachstehender Tabelle). Als mittlere Schadenhöhe µa pro Vertrag erhält man:
µa = S /Na = 3.500 Mio. Euro / 2 Mio. Verträge = 1.750 Euro / Vertrag.
Zu (b):
Wie die Summe von Spalte (4) der Tabelle zeigt, wurden insgesamt Nb = 0,7 Mio. Schadenfälle gemeldet.
Hieraus ergibt sich in der Grundgesamtheit der Schadensfälle die mittlere Schadenhöhe µb pro Schadenfall
zu
µb = S / Nb = 3500 Mio. Euro / 0,7 Mio. = 5 000 Euro
(1)
j
1
2
3
4
(2)
Anzahl der
Schadenfälle
pro Vertrag
zj
(3)
Anzahl der
Verträge
(4)
Anzahl der
Schadenfälle
Nj Mio.]
z j ⋅ Nj [Mio.]
0
1
2
3
1,50
0,35
0,10
0,05
0,00
0,35
0,20
0,15
Na = 2,00
Nb = 0,70
Zu (c):
Aus Spalte (3) der Tabelle liest man ab, dass bei Nc = 0,5 Mio. Verträgen mindestens ein Schadenfall
gemeldet wurde: Somit ist in der Grundgesamtheit der Verträge mit mindestens einem Schadensfall die
mittlere Schadenhöhe µc pro Vertrag mit Schadenfall:
µc = S / Nc = 3500 Mio. Euro / 0,5 Mio. = 7 000 Euro.
Bemerkung: Die drei angegebenen mittleren Schadenhöhen beziehen sich auf drei verschiedene
Grundgesamtheiten. Ihre inhaltliche Bedeutung ist deshalb unterschiedlich. Ein Mittelwert ist nur dann
korrekt interpretierbar, wenn klar ist, auf welche Gesamtheit er sich bezieht. Spricht man z.B. im
vorliegenden Fall verkürzt nur von „mittlerer Schadenhöhe“, so ist diese Angabe unvollständig und daher ggf.
missverständlich oder irreführend.
Lösung zu Aufgabe 14
Zu (a) Mittelwerte :
Der Modalwert ist 3, da gemäß Häufigkeitstabelle 3 die am häufigsten auftretende Ausprägung ist.
Der Zentralwert (Median) Z hat den Wert Z = 3, denn links von Z liegen weniger als 50% der Daten,
nämlich 23 von 50 und auch rechts von Z liegen weniger als 50% der Daten, nämlich 11 von 50.
Das arithmetische Mittel µ errechnet sich als Summe der Produkte von Ausprägung mj mal zugehöriger
relativer Häufigkeit (Nj / N) zu
J
J
Nj
= ( ∑ m j ⋅ N j ) / N = ( 0 ⋅ 1 + 1 ⋅ 8 + 2 ⋅ 14 + 3 ⋅ 16 + 4 ⋅ 9 + 5 ⋅ 2 ) / 50 = 130 / 50 = 2,6.
µ = ∑m j ⋅
N
j=1
j=1
Zu (b) Streumaße :
Die mittlere absolute Abweichung ( = geometrische Durchschnittsentfernung) zum Bezugspunkt c werde
mit Ec bezeichnet. Sie errechnet sich nach der Formel
J
Nj
Ec = ∑ m j − c ⋅
.
N
j=1
Allgemein gilt EMe ≤ Ec für alle reellen Zahlen c (Minimaleigenschaft des Medians).
Setzt man in diese Formel für Ec an Stelle von c die gegebenen Werte mj und Nj sowie Z = 3 bzw. µ = 2,6
ein, so erhält man EZ = 0,920 bzw. Eµ = 0,952.
Die mittlere quadratische Abweichung zum Bezugspunkt c werde mit Qc bezeichnet. Qc berechnet sich
nach der Formel
J
Nj
Qc = ∑ (m j − c)2 ⋅ .
N
j=1
2
Aus der für alle reellen Zahlen c gültigen Beziehung Qµ = Qc + (c − µ) folgt Qµ ≤ Qc , also
J
Nj
Varianz σ2 = Qµ = ∑ (m j − µ)2 ⋅
≤ Qc (Minimaleigenschaft des arithmetischen Mittels)
N
j =1
Setzt man in die Formel für Qc die Werte mj und Nj sowie anstelle von c den Zentralwert Z = 3 bzw.
den Mittelwert µ = 2,6 ein, so erhält man
bzw.
σ2 = Qµ = 1,28 und somit σ = 1,13 .
QZ = 1,44
Weiter gilt allgemein: σ ≥ Eµ , d.h. die Standardabweichung σ (interpretierbar als eine „mit der besonderen
Messlatte der Statistiker gemessene“ statistische Durchschnittsentfernung der Daten zum
„Datenschwerpunkt“ µ ) ist nie größer als die geometrische Durchschnittsentfernung der Daten zu µ .
J
Nj
j=1
N
Die Varianz σ2 läßt sich zwar auch anhand der Formel σ2 = Qµ = ∑ m2j ⋅
J
Nj
j=1
N
bei der man von der Summe ∑ m2j ⋅
− µ2 berechnen. Diese Formel,
das Quadrat des Bezugspunktes µ, abzieht, darf jedoch nicht zu
J
Nj
j=1
N
dem Fehlschluss führen, dass sich QZ analog dazu nach der Formel ∑ m2j ⋅
− Z2 errechnen ließe.
Dass dies nicht zutreffen kann, ist direkt aus der oben angegebenen Formel Qµ = Qc + ( c − µ )
2
erkennbar.
Lösung zu Aufgabe 15
Zu (a):
Falls sich in einem Stabdiagramm die Daten symmetrisch um einen Punkt der Zahlengeraden verteilen, stellt
der Symmetriepunkt das arithmetische Mittel µ der Daten dar. Demnach entnimmt man direkt aus Abb. 1
bis Abb. 3 die Mittelwerte
(1)
µ x = 3,5 < µ z = 4,5 < µ y = 6,5.
Zu (b):
Die Standardabweichung σ misst wie stark die Daten um das arithmetische Mittel µ streuen . Daher ist σ
um so kleiner, je „näher“ die Daten bei µ liegen, d.h. je häufiger die schwerpunktnahen und je seltener die
schwerpunktfernen Ausprägungen auftreten.
Bei den drei Abbildungen haben die Abstände zwischen den Ausprägungen und dem jeweiligen
arithmetischen Mittel jeweils zweimal die Werte 0,5 ; 1,5 und 2,5 , die Häufigkeiten, mit denen diese
Abstandswerte auftreten, sind jedoch bei den einzelnen ABB: unterschiedlich:
In Abb. 1 treten die schwerpunktnahen Ausprägungen seltener auf als in Abb. 2, also ist σx > σy .
In Abb. 1 treten die schwerpunktnahen Ausprägungen häufiger auf als in Abb. 3, also ist σx < σz .
Insgesamt betrachtet besteht also für die Standardabweichungen der drei Merkmale x, y und z die
Relation :
σ y < σx < σz .
(2)
Lösung zu Aufgabe 16
Zu (a):
Aus N = 30 ; Σxi = 450 ; Σ xi2 = 6770,295 folgt mit den Formeln für das arithmetische Mittel und die Varianz
von Urlistendaten (siehe Formelsammlung):
Arithmetisches Mittel : µ = 450/30 = 15,00 [ € ]
2
2
2
Varianz :
σ = 6770,295 / 30 – (15,00) = 0,6765 [ € ]
Standardabweichung : σ = 0,6765 = 0,8225 [€ ]
Variationskoeffizient : v = 0,8225 / 15,00 = 0,0548 = 5,48%.
Zu (b):
Die Einordnung der Löhne in die Lohngruppen führt zu den gruppierten Daten der Tab. 1:
Kl. Nr. Klasseneinteilung
Klassenmitte Abs. Häufigk.
j
mj
Nj
mj ⋅ Nj
1
13,00 bis unter 14,00
13,50
4
54,00
2
14,00 bis unter 14,50
14,25
3
42,75
3
14,50 bis unter 15,00
14,75
6
88,50
4
15,00 bis unter 15,50
15,25
10
152,50
5
15,50 bis unter 17,00
16,25
7
113,75
N =30
451,50
mj2 ⋅ Nj
729,0000
609,1875
1305,3750
2325,6250
1848,4375
6817,6250
Aus den gruppierten Daten der Tabelle ermittelt man zunächst folgende Summen:
5
5
j =1
j =1
N = Σ Nj = 30 ; ∑ m j ⋅ N j = 451,50 [€] ; ∑ m 2j ⋅ N j = 6817,625 [ € ] .
2
Daraus errechnet man dann die gesuchten Kenngrößen:
5
Arithmetisches Mittel : µ = ∑ m j ⋅ Nj / N = 451,50 / 30 = 15,05 [ € ]
j =1
Varianz :
5
σ = ∑ m2j ⋅ Nj /N − µ = 6817,625 / 30 – (15,05) = 0,7517 [ € ]
2
2
2
2
j =1
Standardabweichung : σ = 0,6765 = 0,8670 [€ ]
Variationskoeffizient : v = 0,8670 / 15,05 = 0,0576 = 5,76%.
Bemerkung: Die bei (b) aus den gruppierten Daten berechneten Werte für µ und σ stimmen nicht mit den
bei (a) ermittelten überein. Die Unterschiede sind auf die beim Gruppieren nicht zu vermeidenden
Informationsverluste zurückzuführen.
Zu ( c):
Verbale Lösung: Wenn alle Löhne um 2 [€] erhöht werden, steigen sie auch im Mittel um 2 [€]: Der mittlere
Lohn nach der Lohnerhöhung beträgt also 17 € .
Weil alle Löhne zusammen mit dem Mittelwert um 2 € auf der Lohnskala nach rechts verschoben werden,
verändern sich die Abstände der Löhne zum Mittelwert nicht. Demzufolge bleibt die Streuung der Löhne um
den jeweiligen Mittelwert und damit auch die Varianz und die Standardabweichung unverändert; somit
besitzen die erhöhten Löhne ebenfalls die Standardabweichung σ = 0, 8225 € .
Der Variationskoeffizient hingegen wird kleiner: Bezogen auf das höhere Lohnniveau 17 € streuen die Daten
weniger stark als bezogen auf das Lohnniveau 15 €.
Formale Lösung: Bezeichne xi bzw. yi die Löhne vor bzw. nach der Lohnerhöhung, dann wird der
Zusammenhang zwischen xi und yi beschrieben durch die Lohnformel yi = xi + 2,
also durch eine lineare Funktion yi = a + b ⋅ xi mit a = 2 und b = 1.
Für Mittelwert µy und Standardabweichung σy eines linear transformierten Merkmals gilt allgemein :
und
σy = ⏐b⏐σx .
µy = a + b⋅µx
Hieraus findet man speziell für a = 2 und b = 1 : µy = 15 + 2 = 17 sowie σy = σx = 0, 8225 und weiter
vy = σy / µy = 0,8225 / 17 = 0,484 = 4,84%.
Lösung zu Aufgabe 17
Jeder der 10 angegeben siebenstelligen Zahlenwerte beginnt mit der Ziffer 3 und endet mit 4 Nullen.
6
4
Wählt man a = 3⋅10 und b = 10 , so werden durch die Transformation von xi nach zi die führende
Ziffer 3 und die 4 Nullen am Ende beseitigt. Somit entstehen bei Anwendung der linearen Transformation
6
4
zi = ( xi – a ) / b = ( xi – 3 ⋅ 10 ) / 10
zweistellige Daten zi . Beispielsweise wird x1 = 3 340 000 zu z1 = 34 transformiert.
Aus den zweistelligen zi - Werten errechnet man das arithmetische Mittel µz = 46 und die
Standardabweichung σz = 12.
Bei linearer Verknüpfung xi = a + b⋅zi der Merkmale z und x besteht zwischen den zugehörigen
Mittelwerten bzw. Standardabweichungen die Beziehung µx = a + b⋅µz bzw. σx = ⏐ b⏐⋅ σz . Hieraus ergibt
sich durch Einsetzen von µz = 46 und σz = 12 :
6
4
4
µx = 3 ⋅10 + 10 ⋅ 46 = 3 460 000
und
σx = 10 ⋅12 = 120 000 .
Bemerkung : Bei Verwendung von Taschenrechnern bzw. Computern besteht der Hauptaufwand im
Eintippen der Daten. Bei Nutzung der Transformation von xi zu zi hat man statt siebenstelliger Daten nur
noch zweistellige Daten einzutippen, so dass sich der Tippaufwand um mehr als 70% reduziert.
Lösung zu Aufgabe 18
Für die Daten x1 , ... , xn bezeichne µn = Σxi/n das arithmetische Mittel und σn2 = ∑ (x i − µ n ) 2 /5 die Varianz.
Gegeben ist µ4 = 20 und σ 24 = 25, gesucht ist µ5 und σ52 .
4
1 4
∑ xi =20 folgt ∑ xi = 4 ⋅ 20 = 80 und daraus weiter mit x15 = 15:
4 i=1
i=1
Aus µ4 =
µ5 =
1
[
5
4
∑ xi + x5 ] = 5 ⋅ [80 + 15] =
i=1
Aus σ24 =
σ52 =
1
[
5
1
1
4
4
4
∑
i =1
xi2 − µ24 =
1
4
95
= 19.
5
4
∑
4
xi2 − 202 = 25 folgt zunächst
i=1
∑ xi2 + x25 ] − µ52 = 5 [1700 + 152 ] − 192 = 24.
i=1
1
∑ xi2 = 4⋅[25 + 20 ] = 1700
2
i =1
und daraus weiter: