Knoten und Maschenanalyse
Werbung
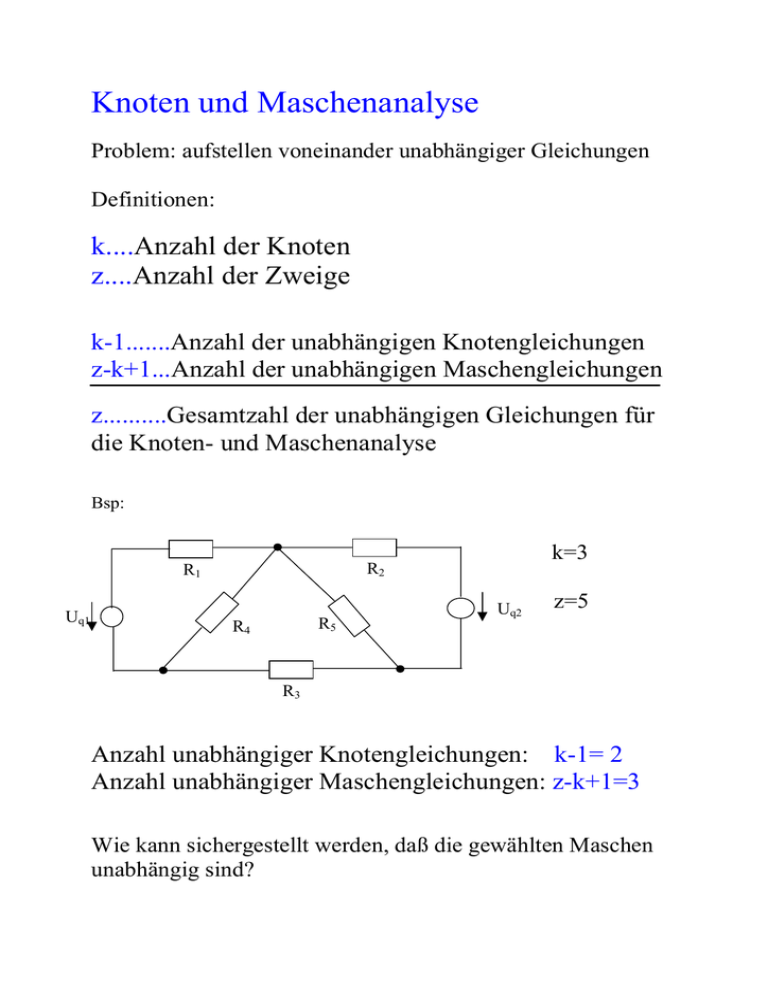
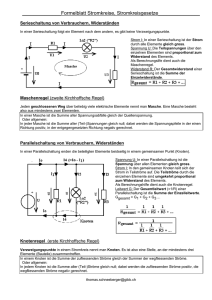
Knoten und Maschenanalyse Problem: aufstellen voneinander unabhängiger Gleichungen Definitionen: k....Anzahl der Knoten z....Anzahl der Zweige k-1.......Anzahl der unabhängigen Knotengleichungen z-k+1...Anzahl der unabhängigen Maschengleichungen z..........Gesamtzahl der unabhängigen Gleichungen für die Knoten- und Maschenanalyse Bsp: Uq1 k=3 R2 R1 R5 R4 Uq2 z=5 R3 Anzahl unabhängiger Knotengleichungen: k-1= 2 Anzahl unabhängiger Maschengleichungen: z-k+1=3 Wie kann sichergestellt werden, daß die gewählten Maschen unabhängig sind? Verfahren des vollständigen Baumes: reduziere das Netzwerk auf Schaltungsschema (=Kanten und Knoten) am Bsp: R2 R1 Uq1 R4 R5 Uq2 R3 Wie wird der Baum gebildet – wodurch ist er gekennzeichnet? 1) er enthält alle k Knoten und k-1 Kanten 2) er enthält keine Zyklen (Maschen) Bsp: 8 mögliche Bäume 3) durch hinzufügen einer Kante entsteht eine Masche (Elementarzyklus). Die Anzahl der möglichen Zyklen gibt die Anzahl der unabhängigen Maschen. Maschenstromverfahren: Gesucht: z Zweigströme Vorteil des Maschstromverfahrens: Nur z-k+1 Gleichungen erforderlich (anstatt z Knoten- und Maschengleichugen) Vorgehensweise: 1) vereinfachen der Schaltung Stromquellen durch Spannungsquellen äquivalent ersetzen nur Widerstände und eingeprägte Spannungen sind enthalten 2) vollständigen Baum markieren ⇒ z-k+1 Zweige bleiben übrig (=Verbindungszweige deren Zählpfeilrichtung (Stromrichtung) beliebig angenommen werden kann) 3) bilden der z-k+1 Maschen (bevorzugt entsprechend der gewählten Zählpfeilrichtung) II I II I2 III 4) Achtung: Bauelemente die zu Zweigen des Baumes gehören, werden von mehreren Maschenströmen durchflossen. I1 I2 R2 R1 Uq1 R4 Uq2 R5 R3 I3 I: R1I1+R4I1-R4I3-Uq1 II: R2I2+R5I2+R5I3-Uq2 III: R3I3+R4I3+R5I3-R4I1+R5I2 =0 =0 =0 In Matrixschreibweise: [R]*[I]=[U] Häufig findet man in der Literatur auch [−U] –die Quellenspannung ist entsprechend zu berücksichtigen (im oder gegen den Umlaufsinn der Masche positiv gezählt) R 1+ R 4 0 -R 4 Uq1 Uq2 0 0 R 2+ R 5 R5 berechnete Größen: I1,I2,I3 -R 4 R5 R 3+ R 4+ R 5 ⇒ I4=I1-I3; I5=I2+I3 ⇒ Ui * I1 I2 I3 Systematisches aufstellen der Matrizen/Vektoren Widerstandsmatrix: • Hauptdiagonale: Summenwiderstände der Masche – immer positiv • An allen anderen Stellen werden gemeinsame Widerstände zweier Maschen eingetragen. 0... kein Widerstand +Ri,j... Zweig von Ii und Ij gleichsinnig durchflossen −Ri,j... Zweig von Ii und Ij gegensinnig durchflossen • die Matrix ist symmetrisch Spannungsvektor: • +Uq... Quellenspannung gegen den Umlaufsinn der Masche • −Uq.... Quellenspannung im Umlaufsinn der Masche bei [−Uq] entsprechend umgekehrt Knotenpotentialverfahren: bestimme Potentiale von k-1 Knoten gegenüber einem definierten 0-Potential k-1 Gleichungen erforderlich Vorgehensweise: 1) Schaltung vereinfachen Spannungsquellen durch Stromquellen äquivalent ersetzen nur Leitwerte und eingeprägte Ströme sind enthalten 2) einführen eines Bezugsknotens mit Potential ϕ=0 alle weiteren Knotenpotentiale relativ zum Bezugsknoten einführen ϕ0 Iq2 Iq1 U10 G1 G5 G4 U20 ϕ1 G3 ϕ2 U20-U10 3) aufstellen von k-1 Knotengleichungen G2 ϕ0 Iq2 Iq1 G1 U10 G4 G5 G2 U20 G3 ϕ1 ϕ2 U20-U10 I: G1U10+G4U10-G3(U20-U10)+Iq1 =0 II: G2U20+G5U20+G3(U20-U10)+Iq2 =0 (in dieser Schreibweise (Gleichung I und II) werden vom Knoten weg fließende Ströme positiv gezählt ) in Matrixschreibweise: [G]*[U]=[I] G1+G4+G3 -G3 -G3 G2+G3+G5 bestimmt: U10, U20 ⇒ U21=U20-U10 ⇒ Ii U10 * U 20 = -Iq1 -Iq2 Systematisches aufstellen der Matrizen/Vektoren Leitwertmatrix • Die Hauptdiagonale enthält die Summe der Leitwerte, die mit dem jeweiligen Knoten verknüpft sind. • An allen anderen Stellen werden die Koppelleitwerte zwischen den Knoten ϕi und ϕj eingetragen. 0... kein Leitwert −Gij...sonst • Die Leitwertmatrix ist symmetrisch. Stromvektor (eingeprägte Ströme) • −Iq wenn vom Knoten weg • +Iq wenn zum Knoten hin