Die Kirchhoffschen Regeln
Werbung

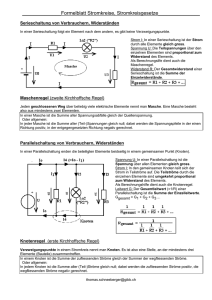
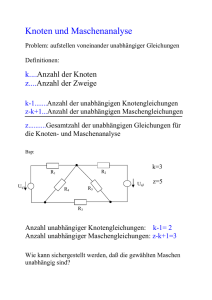
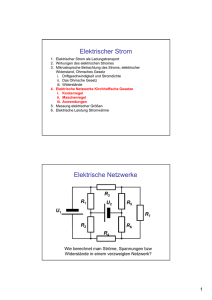
Die Kirchhoffschen Regeln Analyse von Schaltungen mit vernetzen Bauteilen Kirchhoffsche „Maschenregel“ In statischen Feldern sind die Potentiale vom Weg unabhängig • Deshalb ist die Summe über alle Spannungen auf einem beliebigen geschlossenen Weg innerhalb einer Schaltung Null 0 N U i 1 i N Anzahl der Spannungsquellen in der Masche, so heißt ein „geschlossener Weg“ Anleitung zur Kirchhoffschen „Maschenregel“ • Von einem beliebigen Punkt ausgehend bewegt man sich auf einem geschlossenen Weg – in Richtung des technischen Stromflusses, von Plus nach Minus, • und summiert alle Spannungen über den Bauteilen – Spannungen aus Spannungsquellen, die von Minus nach Plus durchlaufen werden, werden mit negativem Vorzeichen in die Summe aufgenommen. Anmerkung: Vorzeichen der Spannung an einer Spule bei Anschluss an eine Spannungsquelle U L ( L I(t )) U R RI U~ U0 *Bei Anschluss einer Spule an eine Spannungsquelle stellt sich der Strom so ein, dass die durch sein Magnetfeld induzierte Spannung gleich der Spannung an der Quelle ist: Das Vorzeichen der Spannung an der Quelle (es sei links momentan „Plus“) überträgt sich deshalb auf die Spule Beispiel für die Analyse einer Schaltung nach der Kirchhoffschen Maschenregel, Umlauf von + nach -, Quellen von + nach – zählen positiv, im Gegensinn durchlaufene negativ Start und Ziel UC Q / C 2U L ( L I(t )) 1 U0 U0 U R1 R1I1 0 U L U R1 U 0 0 U L U C U R 2 U 0 U R 2 R2 I 2 1V Masche 1 1V Masche 2 Analyse der abgeglichenen Wheatstoneschen Brücke nach der Kirchhoffschen Maschenregel, Umlauf von + nach -, Quellen von + nach – zählen positiv, im Gegensinn durchlaufene negativ 2 Start und Ziel R0 Rx 1 1 0 I1 0,5 I2 Start und Ziel R1 R2 U0 I1 R0 I 2 R1 0 1V Masche 1 I1 Rx I 2 R2 0 1V Masche 2 Analyse der abgeglichenen Wheatstoneschen Brücke nach der Kirchhoffschen Maschenregel, Umlauf von + nach -, Quellen von + nach – zählen positiv, im Gegensinn durchlaufene negativ 2 Start und Ziel 1 R0 Rx 10 0,5 Start und Ziel R1 R2 U0 I1 R0 I 2 R1 I1 Rx I 2 R2 Rx / R0 R2 / R1 l2 / l1 1V 1V 1 Masche 1 Masche 2 Nach Division beider Gleichungen Längen am Schiebewiderstand 2 Start und Ziel 1 R0 Rx 10 0,5 Start und Ziel R1~l1 R2~l2 U0 R2 / R1 l2 / l1 Rx R0 l2 / l1 1 Widerstände verhalten sich wie die Längen 1Ω Wert des unbekannten Widerstands Kirchhoffsche „Knotenregel“ In jedem Verzweigungspunkt einer Schaltung, den „Knoten“, muss ebensoviel Ladung zu- wie abfließen • Deshalb ist die Summe über alle Ströme, die in den Knoten münden, Null 0 N I i 1 i N Anzahl der Zweige, die in den Knoten münden Anleitung zur Kirchhoffschen „Knotenregel“ • Man zählt Ströme, die in den Knoten einfließen, positiv, die abfließenden negativ Knoten IL ICR2 IR1 0 I L I CR 2 I R1 Beispiel für die Analyse einer Schaltung nach der Kirchhoffschen Knotenregel Knoten 1 IL ICR2 IR1 U0 I0 IR1 ICR2 Knoten 2 0 I L I CR 2 I R1 0 I CR 2 I R1 I 0 Knoten 1 Knoten 2 Zusammenfassung • Knotenregel: Die Summe über alle Ströme, die in einen „Knoten“ genannten Verzeigungspunkt einer Schaltung münden, ist Null • Maschenregel: Die Summe über alle Spannungen auf einem beliebigen geschlossenen Weg (einer „Masche“) innerhalb einer Schaltung ist Null • Jede Anwendung eines der beiden Kirchhoffschen Gesetze liefert eine Gleichung mit einigen Unbekannten (Spannungen, Strömen, Widerständen, usw.) • Ziel ist, so viele Gleichungen aufzustellen, wie es unbekannte Größen gibt • Die Lösung dieses „linearen Gleichungssystems“ liefert die Unbekannten – Bei mehreren Gleichungen ist die Lösung mit einem geeigneten Programm sinnvoll finis U L L I(t ) Knoten IL ICR2 U0 U0 U R1 R1I1 IR1 0 I L I CR 2 I R1 0 U L U R1 U 0