11 Elektrische Netzwerke
Werbung
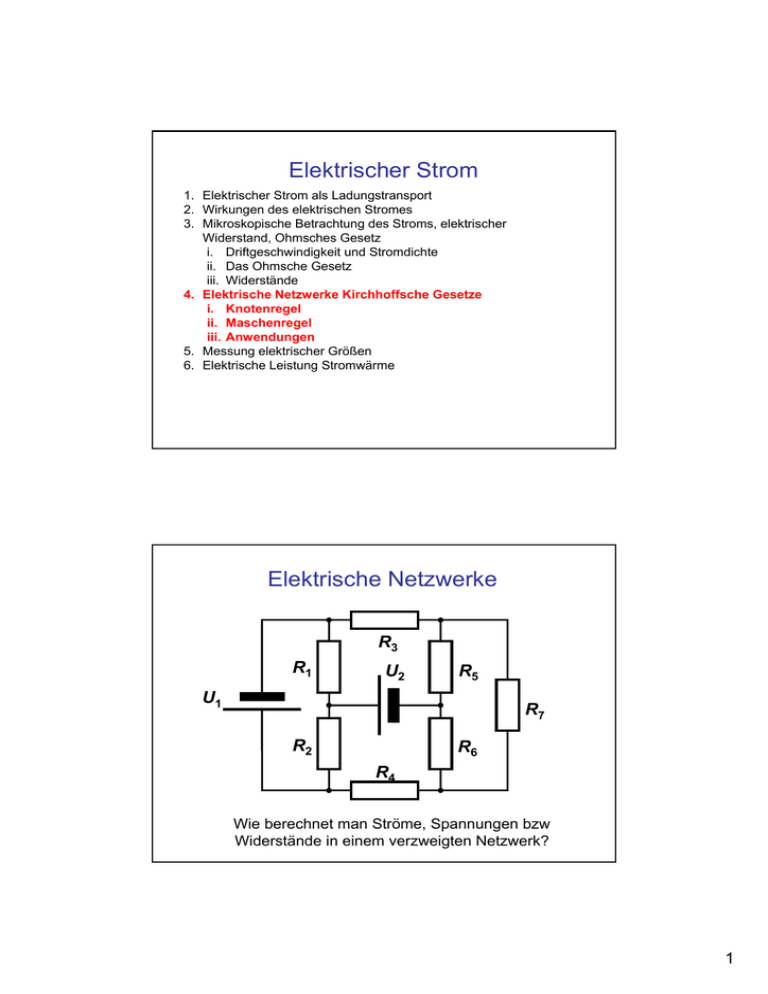
Elektrischer Strom 1. Elektrischer Strom als Ladungstransport 2. Wirkungen des elektrischen Stromes 3. Mikroskopische Betrachtung des Stroms, elektrischer Widerstand, Ohmsches Gesetz i. Driftgeschwindigkeit und Stromdichte ii. Das Ohmsche Gesetz iii. Widerstände 4. Elektrische Netzwerke Kirchhoffsche Gesetze i. Knotenregel ii. Maschenregel iii. Anwendungen 5. Messung elektrischer Größen 6. Elektrische Leistung Stromwärme Elektrische Netzwerke R3 R1 U2 R5 U1 R7 R2 R6 R4 Wie berechnet man Ströme, Spannungen bzw Widerstände in einem verzweigten Netzwerk? 1 Stromkreis Voraussetzung für einen Stromfluss: Potenzialgefälle (Spannungsquelle) Geschlossener Stromkreis „Elektronenstrom“ Idealisiertes Ersatzschaltbild _ Realer Leiter I Schaltbilder: Spannungsquelle: U = const. U + = idealer Leiter I Technische Stromrichtung Ampere hat die Stromrichtung vom Pluspol zum Minuspol festgelegt : technische Stromrichtung Die Elektronen in metallischen Leitern fließen vom Minuspol zum Pluspol: Elektronenstromrichtung Verzweigte Stromkreise Berechnungen in verzweigten Stromkreisen: Vorbereitungen Festlegung von Knoten I1 I2 R1 UR1 U02 R4 U01 + I4 I5 R2 Masche festlegen Richtung der Quellspannung von + nach U03 Ströme einzeichnen Richtung willkürlich R3 Umlaufsinn der Masche festlegen Spannungen in Umlaufrichtung werden positiv gezählt gegen Umlaufrichtung negativ 2 1. Regel von Kirchhoff: Knotenregel In einem Verzweigungspunkt ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme I3 I1 I1 + I2 = I3 + I4 + I5 I4 I2 I5 ∑I i zu i = ∑ Ii ab i Bzw. zählt man zufließende Ströme positiv und abfließende negativ, so ist im Knoten die Summe aller Ströme gleich null ∑I i =0 i Knotenregel und Ladungserhaltung Hüllfläche A, Volumen V I3 I1 I2 I4 r r I i = ∫ j i dA I5 ⇒ auslaufend: I>0 einlaufend: I<0 Kontinuitätsgleichung − r r r r dQ = ∫ j dA = ∑ ∫ j i d A = ∑ I i dt Fläche i i −Teilfläche i Im Knoten keine Ladungen erzeugt oder vernichtet ⇒ dQ/dt = 0 ∑I i =0 i Knotenregel = Ladungserhaltung 3 2. Regel von Kirchhoff: Maschenregel Längs einer geschlossenen Masche ist die Summe aller Quellspannungen plus der Summe aller Spannungsbfälle gleich Null Σ U0i + Σ Ii Ri = 0 I1 R1 I2 U02 UR1 U01 R4 U03 I5 I4 R2 R3 I2R1 - U02 + I4R4 + U03 -I5R3 - I5R2 - U01 = 0 Spannungen im Maschensinn positiv gezählt, sonst negativ Maschenregel und Energieerhaltung Elektrisches Feld ist konservatives Kraftfeld: v r E ∫ ds = 0 Arbeit längs eines geschlossenen Weges = 0 Weg A Integral längs einer Masche (geschlossener Weg): A v v r B v r C v r r E d s = E d s + E d s + + E d s K ∫ ∫ ∫ ∫ Weg A B X = U AB + U BC + K + U XA = 0 ∑U k k =0 B UAB U0 UBC UCD D Summe aller Spannungen ist null R3 C Maschenregel ist Erhaltungssatz: Die Energie, welche die Ladung Q in der Spannungsquelle erhält, ist gleich den Energien, welche sie auf einem Weg zum anderen Pol bei den Widerständen verliert. 4 Serienschaltung von Widerständen R1 I I U0 U0 R2 R R3 Forderung: Es soll in beiden Kreisen der gleiche Strom fließen Masche U0 = I R Masche U0 = I R1 + I R2 + I R3 ⇒ R = R1 + R2 + R3 Serienschaltung: Gesamtwiderstand = Summe der Teilwiderstände Parallelschaltung I I R2 U0 R3 R1 I1 U0 I2 R I3 Forderung: gleicher Strom in beiden Kreisen Knotenregel: I = I1 + I2 + I3 Maschen U0 = I1R1 = U2R2 =U3R3 Masche U0 = I R Daraus folgt I = U0/R1 + U0/R2 + U0/R3 1/R = 1/R1 + 1/R2 + 1/R3 Parallelschaltung: Kehrwert des Gesamtwiderstandes ist Summe der Kehrwerte der Teilwiderstände 5 Innenwiderstand einer Batterie I Ukl Messung der Klemmenspannung als Funktion des Stromes Klemmenspannung nimmt mit zunehmenden Strom ab Unverzweigter Stromkreis Spannungsquelle I Spannungsabfall an R Ukl R U=RI U = Ukl Klemmenspannung Wie verhält sich die Klemmenspannung in Abhängigkeit des Widerstandes? R=∞ ⇒ R=0 ⇒ I=0 Ukl = U0 Leerlaufspannung I endlich groß Ukl = 0 I = Ik Kurzschlussstrom Definition Innenwiderstand Ri = U0/Ik 6 Ersatzschaltbild einer realen Spannungsquelle Ri Ukl U0 U0 Ersatzschaltbild: Reale Spannungsquelle wird durch ideale Quelle mit Leerlaufspannung U0 und Innenwiderstand Ri beschrieben Beschreibung einer Spannungsquelle: lastabhängige Klemmenspannung Angabe der Kennlinie notwendig I Ri Ukl Klemmenspannung an realer Quelle Ukl = U0 - Ri I Ukl R Ukl U0 U0 Ik Strom I Spannungsteiler I X=d U0 U0 Ix x X=0 x x −d R1 = ρ A A R = R1 + R2 R2 = ρ Ux R1 I= R2 Ux Potentiometer (Lautstärke) U R1 + R2 U x = I R2 = U 0 U x = U0 R2 R1 + R2 x d Anwendungen Erzeugung einer bestimmten Spannung Ux Messung einer unbekannten Spannung Ux durch Kompensation (Einstellung bis Ix = 0) 7 Kirchhoffsche Gesetze Kirchhoffsche Gesetze gelten immer und können angewendet werden, wenn der der funktionelle Zusammenhang zwischen Strom und Spannung bekannt ist Ohmscher Widerstand U = R I vollständige Lösung Zeitlich veränderlicher Strom bzw. Spannung U(t) bzw. I (t), Kirchhoffsche Gesetze gelten zu jedem Zeitpunkt (quasistationäre Verhältnisse) Lösungen zeitabhängig Aktive Bauelemente (Operationsverstärker, Transistor..) „Black box“ nur notwendig zu wissen Zusammenhang zwischen Eingangs- und Ausgangsgrößen Quasistationäre Netzwerke Zum Zeitpunkt t = 0 wird Schalter geschlossen: Kondensator mit Kapazität C ist anfangs ungeladen Q(t=0)= 0 und wird geladen. Wie verläuft Spannung und Strom an C R I U0 Q UR Masche U0 = UR + UC = RI(t ) + d dt 1 Q(t ) C Q(t = 0 ) = 0 C UC UR = I R und Uc = Q/C dI 1 dQ + dt C dt dQ dI 1 dI 1 mit I = folgt R+ I=0⇒ =− I dt C dt RC dt 0=R U Berücksichtigung der I(t = 0 ) = 0 Anfangsbedingung: R Lösung der DGL mit Ansatz I = I(t =0) exp(-t/τ) weil Uc (t = 0 ) = Q (t = 0 ) =0 C 8 Laden eines Kondensators 2 Strom durch den Kondensator I(t ) = U0 ⎛ t⎞ exp⎜ − ⎟ , R ⎝ τ⎠ τ = RC UR U0 × Spannung am Widerstand UR ⎛ t⎞ UR (t ) = I (t )R = U 0 exp⎜ − ⎟ , ⎝ τ⎠ τ = RC τ t τ t UC Kondensatorspannung: UC (t ) = 1 e ⎛ Q(t ) 1 ⎛ t ⎞⎞ = ⋅ ∫ I(t′)dt′ = U0 ⋅ ⎜⎜1 − exp⎜ − ⎟ ⎟⎟ C C 0 ⎝ τ ⎠⎠ ⎝ t U0 Zu jedem Zeitpunkt gilt: U0 = UR + UC Netzwerke mit aktiven Bauelementen Operationsverstärker (OPV) Ub Versorgungsspannung Uaus Verstärkt die Spannungsdifferenz UD = Up – Un mit großer Verstärkung V0 zur Ausgangsspannung Uaus Uaus = V0 (Up –Un) = V0 UD V0 typischerweise 105 bis 106 Der Eingangswiderstand Ri ist sehr groß (MΩ bis TΩ), es fließt (praktisch) kein Strom in den OPV 9 Rückkopplung + Uein= Up - Un V0 Uaus k U aus = V0 (U p − U n ) Definition der Verstärkung eines OPV U p = U ein Eingangssignal U n = kU aus Invertierender Eingang mit Ausgang verbunden U aus = V0 (U ein − kU aus ) V= U aus V0 = U ein 1 + kV0 V0 → ∞ ⇒ V ≅ 1 k Gesamtverstärkung des rückgekoppelten OPV Für großes V0 des OPV hängt V nicht mehr von V0 ab, sondern nur mehr von der Rückkopplung Goldene Regeln 1.) Die Rückkopplung funktioniert nur, wenn die Ausgangsspannung auf den invertierenden Eingang zurückgeführt wird. Sonst Mitkopplung, die Ausgangsspannung nimmt den positiven oder negativen Maximalwert an 2.) Die Ausgangsspannung stellt sich immer so ein, dass die Differenzspannung Ud = 0 wird (Uaus = V0 Ud, wenn V0 →∞, dann Uaus nur endlich, wenn Ud →0 ) 3.) Die Eigenschaften der Schaltung werden nur durch die äußere Beschaltung bestimmt, d.h. V0 spielt keine Rolle und kommt im Ergebnis nicht vor 4.) Die Eingangsströme in den OPV sind immer 0 10 Elektrometerverstärker + Uein= Up - V0 R1 Un Uaus R2 U p = U ein U n = kU aus = V= R2 U aus R1 + R2 U aus V0 1 R + R2 R = ≅ = 1 = 1+ 1 U ein 1 + kV0 k R2 R2 Anwendung: Verstärker mit großem Eingangswiderstand Elektrometerverstärker Uein M1 Ud + - Un V0 Iin R1 I Uaus M2 R2 Kirchhoffsche Regeln: Masche M1 und M2 M1 : U ein = U d + U n = U d + (I − I in )R2 M 2 : U aus = IR1 + (I − Iin )R2 Goldene Regeln: Ud = 0 Iin = 0 V= U aus R = 1+ 1 U ein R2 Anwendung: Verstärker mit großem Eingangswiderstand 11 Invertierender Verstärker R1 I1 K1 Ud Iin Uein I2 + M1 R2 M2 V0 Uaus Up=0 Masche 1: Uein = IR1+ Ud Masche 2: Uaus = IR2+ Ud Knoten K1: I1 + I2 = Iin ⇒ I1 = - I2 Goldene Regeln: Ud = 0 Iin = 0 V= U aus R =− 2 U ein R1 V < 0: Polarität der Spannung geändert (invertierender Verstärker) Zusammenfassung •Verzweigte Stromkreise werden mit den Kirchhoffschen Regeln berechnet, diese sind Knotenregel (Σ I = 0) und Maschenregel (Σ U = 0) •Die Knotenregel beruht auf der Ladungserhaltung, die Maschenregel auf der Energieerhaltung •Bei der Serienschaltung von Widerständen addieren sich die Teilwiderstände, bei der Parallelschaltung werden die Leitwerte (reziproker Widerstand) addiert •Eine reale Spannungsquelle kann mit einem Ersatzschaltbild bestehend aus idealer Spannungsquelle und Innenwiderstand beschrieben werden. •Die Kirchhoffschen Gesetze können auch zur Analyse von Netzwerken unter quasistatischen Bedingungen herangezogen werden. •Ein Operationsverstärker ist ein Verstärker die Differenz zweier Eingangsspannungen mit hoher Verstärkung verstärkt. •Die Eigenschaften eines rückgekoppelten (idealen) Verstärkers werden ausschließlich durch die Eigenschaften des Rückkoppelnetzwerkes definiert 12