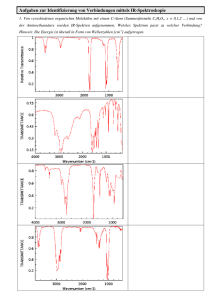
Grundlagen der Spektroskopie

PC III: Grundlagen der
Spektroskopie
Peter Hamm
• Elektronische Spektroskopie (UV-VIS)
• Schwingungsspektroskopie (FTIR und Raman)
• (Rotationsspektroskopie)
• NMR-Spektroskopie
Bücher:
- Atkins: Physikalischer Chemie
- Atkins und Friedman: Molecular Quantum Mechanics
NMR
Spektroskopie
Rotations-
Schwingung-
elektronische
X-ray
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
p*
n
p
N-Methylthioacetamid
nm
Propenal in CCl4
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Absorbance [norm.]
N-Methylthioacetamid
C N
cis
C-C-N-C
trans
1400
1500
1600
-1
Frequency [cm ]
Absorbance [norm.]
CO2 in Wasser
2300
2320
2340
2360
-1
Frequency [cm ]
2380
2400
Absorbance [norm.]
CO2 in Luft
2300
2320
2340
2360
-1
Frequency [cm ]
2380
2400
Absorbance [norm.]
CO2 in Edelgasmatrix (10 K)
2300
2320
2340
2360
-1
Frequency [cm ]
2380
2400
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Rotationsspektrum von HCl
Absorbance [norm.]
Rotations-Schwingungsspektrum
von CO2
2300
2320
2340
2360
-1
Frequency [cm ]
2380
2400
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
S2
S1
DEel
DErot
S0
Hˆ tot  Hˆ el  Hˆ vib  Hˆ rot
DErot  DEvib  DEel
DEvib
Wechselwirkung von Licht mit Materie
Absorption
|1
hn
|0
hn  E1  E0
Gitterspektrometer (UV/VIS)
Gitter
Lampe
Linse
Probe
Linse
Spektrometer
Intensity
I0(n)
I(n)
n
Lambert-Beersche Gesetz
I (n )
A
 (n )cl
 10  10
I 0 (n )
Integrierter Extinktionskoeffizient
  (n )dn  
ˆ
  0  1
2
ˆ
 e  0 x 1
2
2
01
 01: Übergangsdipolmoment
n
Verknüpfung
Spektroskopie ↔ Quantenmechanik
E1, 1
Frequenz:
hn  E1  E0
hn
E0, 0
Integrierter Extinktionskoeffizient:
  (n )dn  01
2
ˆ
  0  1
2
ˆ
 e  0 x 1
2
 x   x 
   

 01    y   e y 
   z
 z  
Crystalline Acetanilid
b-Axis
a-Axis (5)
c-Axis (5)
 x   x 
   

 01    y   e y 
   z
 z  
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Kurze Wiederholung PCII
ˆ
H( x)  E( x)
Zeitunabhängige Schrödingergleichung
Beispiel: H2-Molekül
2
2
ˆ
p
e
1
e
1
1
ˆ
H


(1)
2m 4p 0 ra
4p 0 rb (1)
2
e-
ra(1)
p+
rb
R
ra
(1)
r12
p+
rb(2)
(2)
e-
2
2
ˆp2 2
e
1
e
1



( 2)
2m 4p 0 ra
4p 0 rb ( 2 )
e
2
1

4p 0 R
e2
1

4p 0 r12
Konzepte zur näherungsweise Lösung der
SGL: LCAO Ansatz (Variationsprinzip)
Schrödingergleichung  Operatorgleichung/Differentialgleichung:
 2 2

ˆ
 V ( x)   ( x)  E   ( x)

2
 2m dx

Atomorbitale als Basis:
   cii
i
Entwickeln in dieser Basis  Matrizen-Eigenwertgleichung
Hc  S c
mit
H ij   dxdydz  i* Hˆ  j
Sij   dxdydz i* j
Hückeltheorie:
- nur p-Elektronen
- vollständig parametrisiert
- Überlappintegrale vernachlässigt
Extended Hückeltheorie:
- nur Valenzelektronen
- Ionisierungsenergien und Zeff
parametrisiert.
- aber: Überlappintegrale ‚exakt‘
- semi-empirisch
H2+:
- ‚ab initio‘: startet von Schrödingergleichung, keine Parameter
- Näherung, da Basis endlich
- aber: nur ein Elektron
ab initio Behandlung von Mehrelektronensystemen:
- Hartree Fock, Dichtefunktionaltheorie,
Configuration Interaction
Hückeltheorie: Benzol
LUMO
HOMO
N2
4s*
2p*
2px,2py, 2pz
3s
1p
2px,2py, 2pz
2s*
2s
2s
1s
Heteronukleare Bindung: CO
4s*
C2p
2p*
3snb
C2s
O2p
1p
2snb
1s
O2s
N2
4s*
S0 S1
HOMOLUMO
s  p*
2p*
2px,2py, 2pz
3s
1p
2px,2py, 2pz
2s*
2s
2s
1s
s  p*
 x  e  s x  p *  e   s x p *dxdydz


·x·
·

dxdydz
dxdydz= 0
s  p*
 y  e   s y p *dxdydz


·y·
·

dxdydz
dxdydz= 0
s  p*
 z  e   s z p *dxdydz


·z·
·

dxdydz
dxdydz= 0
N2
4s*
S0 S2
HOMO-1LUMO
p  p*
2p*
2px,2py, 2pz
3s
1p
2px,2py, 2pz
2s*
2s
2s
1s
p  p*
 x  e   p x p *dxdydz


·x·
·

dxdydz
dxdydz 0
p  p*
 y  e   p y p *dxdydz


·y·
·

dxdydz
dxdydz= 0
p  p*
 z  e   p z p *dxdydz


·z·
·

dxdydz
dxdydz= 0
CO
n  p*
4s*
C2p
2p*
3snb
C2s
O2p
1p
2snb
1s
O2s
n  p*
 x  e   n x p *dxdydz



·x·
dxdydz
·
dxdydz= 0
n  p*
 z  e   n z p *dxdydz



·z·
dxdydz
·
dxdydz 0
p*
n
p
N-Methylthioacetamid
Verknüpfung
Spektroskopie ↔ Quantenmechanik
E1, 1
Frequenz:
hn  E1  E0
hn
E0, 0
Integrierter Extinktionskoeffizient:
  (n )dn  
2
01
ˆ
  0  1
2
ˆ
 e  0 x 1
2
 x 
 

 01    y 
 
 z
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Lampe
Linse
Probe
Linse
Spektrometer
I (n )
 10 A  10 (n )cl
I 0 (n )
Intensity
I0(n)
I(n)
n
Gitterspektrometer (UV/VIS)
Gitter
FTIR Spektrometer
50% Strahlteiler
Dx
Detektor
FTIR Spektrometer
I (n , Dx)  I (n )1  cos(2pnDx / c)


0
0
I (Dx)   I (n )1  cos(2pnDx / c) dn  const   I (n ) cos(2pnDx / c)dn
Inverse Fourier Transformation →
I (n )
Lampe
Linse
Probe
Linse
Spektrometer
I (n )
 10 A  10 (n )cl
I 0 (n )
Intensity
I0(n)
I(n)
n
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
H2+-Molekül: LCAO Ansatz
Basis: Atomorbitale

(a)
1s

,  ,
(b )
1s
2s u  1s
(a)
 1s
(b )
1(sa )
1(sb)
1s g  1s
(a)
 1s
(b)
H2+-Molekül: LCAO Ansatz
Basis: Atomorbitale

(a)
1s
eV 4

,  ,
(b )
1s
2s u  1s
3
 1s
(a)
(b )
2
Antibindendes
Orbital
1
1
-1
-2
2
3
1s g  1s
(a)
4 R/Å
 1s
(b)
Bindendes
Orbital
HONO: Schwingungsgrundzustand
HONO: Streckschwingung
HONO: Torsionsschwingung
HONO: Biegeschwingung
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
H2+-Molekül: Harmonische Näherung
E/H
0.02
2
4
6
8
R/a0
-0.02
-0.04
-0.06
Taylorentwicklung:
V
V ( R)  V ( Re ) 
R
1  2V
R  Re  
2
2

R
R  Re
R  Re 2  
R  Re
Harmonischer Oszillator
m1
k
m2
V(x)
x
Harmonischer Oszillator
k

V(x)
mit:
m1  m2

m1  m2
x
Harmonischer Oszillator
k
k 2
V ( x)  x
2

H  E
m2
V(x)
  
k 2
 
 x   E
2
2 
 2  x
2
2
x
Lösungen: Harmonischer Oszillator
n ( y)  H n ( y)e
mit
k 2
y 
x
2

2
1
 y2
2
1

En    n   n  0,1,2,...
2

mit  
k

Harmonischer Oszillator
Harmonischer Oszillator:
Übergangsdipolmoment

mn  m  n

d
m R n
dR
Auswahlregeln:
• Zweiatomiges Molekül: Permanentes
Dipolmoment
• Dn=±1
• Hochfrequente Moden bei nicht zu
hohen Temperaturen (  kBT): 01
Born Oppenheimer Approximation
Hˆ  Tˆel  Tˆnuc  Vˆel,nuc
solve electronic SEQ
Hˆ el el (r; R)  Eel (R)el (r; R)
Eel (R)
is potential energy surface on which nuclei move
solve vibrational SEQ by reintroducing:
Hˆ nucnuc (R)   nuc (R)
with
Tˆnuc
Hˆ nuc  Tˆnuc  E(R)
total wavefunction:
tot  el (r; R)nuc ( R)
Transition dipole for vibration
 S0
S0
  el (r ; R)i ( R) er el (r ; R ) j ( R)
integrate over r:
  i ( R) el ( R)  j ( R)
Taylor expansion:
el ( R)  el ( Req ) 
del ( Req )
dR
 R  Req 
R  Req
i ( R)  el ( Req )  j ( R )   el ( Req ) ij
dˆ el ( R )
i ( R) R  j ( R)
dR
static dipole
transition dipole Dn  1
CO2: Normalmoden
Symmetrische Streckschwingung 1388 cm-1
Asymmetrische Streckschwingung 2349 cm-1
Biegeschwingung, 2-fach entartet 667 cm-1
Anzahl Normalmoden:
• allgemein:
3N-6
• lineares Molekül: 3N-5
d

01 
0 x 1
dx
CO2: Normalmoden
n1 ?
nas(OCO)
n3
s,deg OCO
n
2
mi 2 1
ˆ
H   xi   xi K ij x j
2
2 ij
i
Massegewichtete Koordinaten:
2

qi
1
ˆ
H 
  qi Fij q j
2 2 ij
i
qi  mi xi
mit: Fij 
K ij
mi m j
Normalmodentransformation
(i. e. Eigenwerte und Vektoren von F):
2 1
Q
2
Hˆ   i   i Qi
2 2 i
i
N entkoppelte Oszillatoren mit:
Ei  i ni  1/ 2
mit:
i  i
CO2: Normalmoden
k
m1
x1
k
m2
x2
m1
x3
1
1
1
2
2
V  k x1  x2   k x3  x2    K ij xi x j
2
2
2 i, j
 k

mit K    k
 0

k
2k
k

k

 m1
0 


k

F


 k  oder
m1m2


k 

0


k

m1m2
2k
m2
k

m1m2


0

k 


m1m2 

k

m1

CO2: Normalmoden
1  0
k
2 
m1
2km1  km2
3 
m1m2
 1

m2
A
 mm
1 2

 1
1
0
1
1
2 m1m2

m2
1
k
Translation:






k
0 cm-1
m1
Symmetrische Streckschwingung: 1388 cm-1
Asymmetrische Streckschwingung: 2349 cm-1
m2
m1
CO2: Normalmoden
1  0
2 
k
m1
2km1  km2
3 
m1m2
1
1  1



A'  1 0  2m1 m2 
1 1

1


k
Translation:
k
0 cm-1
m1
Symmetrische Streckschwingung: 1388 cm-1
Asymmetrische Streckschwingung: 2349 cm-1
m2
m1
CO2: Normalmoden
Symmetrische Streckschwingung 1388 cm-1
Asymmetrische Streckschwingung 2349 cm-1
Biegeschwingung, 2-fach entartet 667 cm-1
Anzahl Normalmoden:
• allgemein:
3N-6
• lineares Molekül: 3N-5
d

01 
0 x 1
dx
CO2: Normalmoden
n1 ?
nas(OCO)
n3
s,deg OCO
n
2
Hessian Matrix
2
ˆ
p
1
i
ˆ
H 
  xi Kij x j
2 ij
i 2mi
Taylorentwicklung:
V
V ( x )  V (0)  
i xi
 2V
 K ij 
xi x j
1
 2V
xi  
2 i , j xi x j
x 0
i
xi  x j 0
xi x j  
xi  x j 0
Normal Modes Benzene
Formaldehyd: Normal Modes
2783 cm-1
1746 cm-1
1500 cm-1
1167 cm-1
2843 cm-1
1249 cm-1
Anharmonizität: CO2
Four vibrational modes, two of them degenerate
Two bands in IR nas(OCO), n3 = 2349 cm-1 and
s,deg OCO, n2 = 667 cm-1
One band in Raman ns(OCO), n1= 1388 cm-1, not seen in IR
n1+ n3
Combination bands
(NIR)
2n2+ n3
nas(OCO)
n3
s,deg OCO
n
Fundamental bands
2
Anharmonizität: CO
Overtone band (NIR)
2n(CO)
n(CO)
Expanded
Morsepotential
V

V  De 1  e

 a ( R  Re ) 2
1
1


En   n      x n  
2
2


2
mit:


 a und x 
4 De

De
2De
Dn=±1 Auswahlregel aufgeweicht
Re
R
Anharmonizität: CO2
Four vibrational modes, two of them degenerate
Two bands in IR nas(OCO), n3 = 2349 cm-1 and
s,deg OCO, n2 = 667 cm-1
One band in Raman ns(OCO), n1= 1388 cm-1, not seen in IR
n1+ n3
Combination bands
(NIR)
2n2+ n3
nas(OCO)
n3
s,deg OCO
n
Fundamental bands
2
Elektrische und mechanische Anharmonizität
Elektrische Anharmonizität: Höhere-Ordnung Terme
in der Taylorentwicklung des Dipoloperators:

m  n
d


 m x  n  ...
dx
Mechanische Anharmonizität: Höhere-Ordnung Terme
in der Taylorentwicklung der Potentialfläche:
1  2V
V ( R)  V ( Re ) 
2 R 2
R  Re 2  
R  Re
Leiteroperatoren:
 p 2 k 2 p 2  2 m 2
H
 xˆ 

xˆ
2m 2
2m
2
mit
m

x' 
xˆ


p' 

1 
p
m
2

 p'
xˆ '2 

H   

2 
 2
Leiteroperatoren:
definiere:

1
xˆ  ipˆ 
a
2
1
a  a†
oder: xˆ 
2

1
xˆ  ipˆ 
a 
2
†


[a, a† ]  aa†  a†a  1
mit:
a a n  Nˆ n  n n
†

1
pˆ   i a  a †
2

(folgt aus: [ x , pˆ ]  i )

1
 †
H    a a  

2

†
a n  n  1 n  1 Aufsteigeoperator
a n  n n 1

Absteigeoperator
Besetzungszahloperator
Elektrische Anharmonizität:Oberton
d
1 d 2 2
 (Q)  0 
Q
Q  ...
2
dQ
2 dQ
Oberton:
d
1 d 2
2
2 ˆ 0 
2Q0 
2
Q
0  ...
2
dQ
2 dQ
Elektrische Anharmonizität: Kombinationsmode

2
  0  
Qi  
QiQ j  ...
i Qi
i , j Qi Q j
Kombinationsmode:
1i1 j ˆ 0i 0 j



1i Qi 0i 1 j 0 j 
1i 0i 1 j Q j 0 j
Qi
Q j
2

1i Qi 0i 1 j Q j 0 j  ...
Qi Q j
Anharmonizität: CO2
Four vibrational modes, two of them degenerate
Two bands in IR nas(OCO), n3 = 2349 cm-1 and
s,deg OCO, n2 = 667 cm-1
One band in Raman ns(OCO), n1= 1388 cm-1, not seen in IR
n1+ n3
Combination bands
(NIR)
2n2+ n3
nas(OCO)
n3
s,deg OCO
n
Fundamental bands
2
Mechanische Anharmonizität: Fermiresonanz CO2
Mehr symmetrische
Streckschwingung n1
Mehr Oberton
Biegeschwingung n2
Mechanische Anharmonizität: Fermiresonanz
Absorbance
Benzoylchloride
1720
1760
1800
-1
Wavenumber [cm ]
Mechanische Anharmonizität:
Fermiresonanz mit einem Oberton
1
 2V 2 1
 3V
2
V  V0  
Qi  
Qi Q j  ...
2
2
2 i Qi
2 i , j Qi Q j
Vanh
Kopplung:
1i 0 j Vanh 0i 2 j
wenn:
1  3V
2

1i Qi 0i 0 j Q j 2 j
2
2 Qi Q j
i  2 j
1i  2 j
1i
1i  2 j
 i
0i
2j
 j
1j
 j
0j
Mechanische Anharmonizität:
Fermiresonanz mit einem Oberton
1

0i 0 j ˆ 1i 0 j  0i 2 j
2
1

0i 0 j ˆ 1i 0 j  0i 0 j ˆ 0i 2 j
2
1

0i ˆ 1i
2



wenn:
i  2 j
1i  2 j
1i
1i  2 j
 i
0i

2j
 j
1j
 j
0j
Mechanische Anharmonizität: Fermiresonanz
mit einer Kombinationsmode
1
V 2 2
 3V
V  V0  
Qi  
Qi Q j Qk  ...
2
2 i Qi
i , j , k Qi Q j Qk
Vanh
Kopplung:
1i 0 j 0k Vanh
wenn: i
 3V
0i1 j1k 
1i Qi 0i 0 j Q j 1 j 0k Qk 1k
Qi Q j Qk
  j  k
1i
1 j1k
1i  1 j1k
 i
0i
1i  1 j1k
k
 j
1 j 0k
0 j 0k
Mechanische Anharmonizität: Fermiresonanz
Absorbance
Benzoylchloride
1720
1760
1800
-1
Wavenumber [cm ]
Raman Spektroskopie
Probe
Spektrometer
Linse
GaAs
cw-Laser
Raman Spektroskopie
Polarisierbarkeit: ind  
d
R  Req   ...
 ( R)   Req  
dR
Durch eine Schwingung wird R zeitabhängig:
R  Req  DR cos(vibt )

 (t )  eq  D cos(vibt )
mit
d
D 
DR
dR
Wenn wir Licht einstrahlen (nicht-resonant mit dem Schwingungsübergang,
und nicht-resonant mit elektronischen Übergang ):
 (t )   0 cosopt t 

ind (t )   (t ) (t )
  0  D cosvibt  0 cosopt t 

  0 0 cosopt t   D 0 cosopt  vib t  cosopt  vib t
Raleigh
Anti-Stokes
Stokes

Raman Spektroskopie
 mn
d

m R n
dR
Auswahlregeln:
• Zweiatomiges Molekül: immer
• Mehratomiges Molekül mit Inversionssymmetrie: IR-aktiv und
Raman aktiv schliessen sich gegenseitig aus
• Dn=±1
Schwingungsspektroskopie CO2
Symmetrische Streckschwingung 1388 cm-1
Raman-aktiv
Asymmetrische Streckschwingung 2349 cm-1
IR-aktiv
Biegeschwingung, 2-fach entartet 667 cm-1
IR-aktiv
CO2: Normalmoden
Raman Spektroskopie: CO2
Fermiresonanz: Streckschwingung
+ Oberton Biegeschwingung
Raman Spektroskopie: Quantenmechanische
Beschreibung
GaAs
Raman Spektroskopie
Polarisierbarkeit: ind  
d
R  Req   ...
 ( R)   Req  
dR
Durch eine Schwingung wird R zeitabhängig:
R  Req  DR cos(vibt )

 (t )  eq  D cos(vibt )
mit
d
D 
DR
dR
Wenn wir Licht einstrahlen (nicht-resonant mit dem Schwingungsübergang,
und nicht-resonant mit elektronischen Übergang ):
 (t )   0 cosopt t 

ind (t )   (t ) (t )
  0  D cosvibt  0 cosopt t 

  0 0 cosopt t   D 0 cosopt  vib t  cosopt  vib t
Raleigh
Anti-Stokes
Stokes

Raman Spektroskopie
Polarisierbarkeit: ind  
d
R  Req   ...
 ( R)   Req  
dR
Durch eine Schwingung wird R zeitabhängig:
R  Req  DR cos(vibt )   (t )  eq  D cos(vibt )
mit
d
D 
DR
dR
Klassisch:
thermische Anregung
Quantum-mechanisch:
„Nullpunkts-Schwingung“ + thermische Anregung
Raman Spektroskopie: Quantenmechanische
Beschreibung
virtuelles Niveau
virtuelles Niveau
opt  vib 
opt
Stokes
opt
opt  vib 
n=1
n=1
n=0
n=0
Anti-Stokes
Raman Spektroskopie: Quantenmechanische
Beschreibung
I AntiStokes
e
I Stokes
GaAs
 vib
k BT
Resonanz-Raman Spektroskopie
Elektronischer Übergang
opt  vib 
opt
Stokes
opt
opt  vib 
n=1
n=1
n=0
n=0
Anti-Stokes
Resonanz-Raman Spektroskopie: Bacteriorhodopsin
3 ps
0.5 ps
J
K
2 μs
L
50 μs
ms
O
ms
M
N
ms
Mathies, 1987
Resonanz-Raman Spektroskopie: Bacteriorhodopsin
3 ps
0.5 ps
J
K
2 μs
L
50 μs
ms
O
ms
M
N
ms
Mathies, 1987
IR Spektroskopie: Bacteriorhodopsin
2.0
D2O
Absorbance
1.5
1.0
Amide 2
0.5
0.0
1000
1100
1200
1300
1400
1500
-1
Frequency [cm ]
Amide I
1600
1700
Zusammenfassung: Schwingungsspektroskopie
• Zwei komplementäre Messmethoden: IR-Absorptionsspektroskopie und Ramanspektroskopie
• 3N-6(5) Normalmoden
• in harmonischer Näherung und Dipolnäherung: maximal
3N-6(5) Banden:
Auswahlregel Dn=±1
IR- aktiv:
d/dR ≠0
Raman-aktiv: d/dR ≠0
• Mehratomiges Molekül mit Inversionssymmetrie: IR-aktiv
und Raman aktiv schliessen sich gegenseitig aus
• Anharmonizität  Obertöne, Kombinationsmoden,
Fermisresonanz (meist klein)
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Benzol
925 cm-1
995 cm-1
Heteronukleare Bindung: CO
4s*
C2p
2p*
3snb
C2s
O2p
1p
2snb
1s
O2s
Übergang zwischen zwei elektronischen Potentialflächen
Energy
S1
S0
R
Franck-Condon Prinzip: klassische Beschreibung
S1
10fs
„<1fs“
S0
R
„senkrechter Übergang“
Franck-Condon Prinzip: quantenmechanisch
S1
   el vib ˆ el  'el  'vib
  el ˆ el  'el  vib  'vib
S0
R
elektronisches
Dipolmatrixelement
Franck-Condon
Faktor
nicht Franck-Condon aktiv
n=2
FC  0
( S0 )
n
( S1 )
2
n=1
n=0
n=0
R
(0,0)
(0,1)
(0,2)
(0,3)
(0,4)
Frequenz
schwach Franck-Condon aktiv
n=2
FC  0
( S0 )
n
( S1 )
2
n=1
n=0
n=0
R
(0,0)
(0,1)
(0,2)
(0,3)
(0,4)
Frequenz
stark Franck-Condon aktiv
n=2
FC  0
( S0 )
n
( S1 )
2
n=1
n=0
n=0
R
(0,0)
(0,1)
(0,2)
(0,3)
(0,4)
Frequenz
Franck-Condon Prinzip: klassisch  QM
n=2
n=1
n=0
n=0
R
R
Der senkrechte Übergang ist der intensivste
Benzol
925 cm-1
995 cm-1
0-14
n=0
0-15
0-16
Vibronisches Spektrum I2
Aus. B. Snadden J. Chem Education 64 (1987) 919
1-14
n=1
1-15
n=2
Vibronische Übergänge in mehratomigen Molekülen
R2
R2
R1
Vibronische Übergänge in mehratomigen Molekülen
R2
R1
R1
Eine stark Franck-Condon aktive Mode, hohe Frequenz
00
01
02
03
04
Eine stark Franck-Condon aktive Mode, hohe Frequenz
+ eine schwach Franck-Condon aktive Mode, niedrige Frequenz
0,01,0
0,00,0
0,02,0
0,03,0
0,01,1
0,00,1
0,2
0,04,0
1,2
0,3
1,3
  el1,vib2,vib ˆ el  'el  '1,vib  '2,vib
 el ˆ el  'el 1,vib  '1,vib 2,vib  '2,vib
Evib  E1,vib  E2,vib
0,0  0,0
gleichzeitige Anregung
R2
R1
0,0  1,0
gleichzeitige Anregung
R2
R1
0,0  0,1
gleichzeitige Anregung
R2
R1
0,0  1,1
gleichzeitige Anregung
R2
R1
Eine stark Franck-Condon aktive Mode, hohe Frequenz
+ eine schwach Franck-Condon aktive Mode, niedrige Frequenz
FC  1,vib  '1,vib  2,vib  '2,vib
Evib  E1,vib  E2,vib
0,01,0
0,00,0
0,02,0
0,03,0
0,01,1
0,00,1
0,2
0,04,0
1,2
0,3
1,3
Franck-Condon Übergang CO2
asymmetrische Streckschwingung:
nicht Franck-Condon aktiv
symmetrische Streckschwingung:
Franck Condon aktiv
Benzol
925 cm-1
995 cm-1
Totally symmetric C-C Stretch Vibration: 995 cm-1
asymmetric C-C Stretch Vibration: 1010 cm-1
Franck-Condon Übergang Benzol
asymmetrische Streckschwingung:
nicht Franck-Condon aktiv
symmetrische Streckschwingung:
Franck Condon aktiv
Resonanz-Raman Spektroskopie
opt  vib 
opt
n=1
n=0
Stokes
„1fs“
n=1
n=0
Raman-aktiv  Franck-Condon aktiv
Auswahlregeln: Franck-Condon Übergang
• Symmetrie: Raman-aktiv  Franck-Condon aktiv
• Molekül mit Inversionssymmetrie: IR-aktiv und FranckCondon aktiv schliessen sich gegenseitig aus
• Moden die stark resonanz-Raman aktiv sind, sind auch
stark Franck-Condon-aktiv
• Im Gegensatz zur Ramanspektroskopie: keine Dn=±1
Auswahlregel
Benzol
925 cm-1
995 cm-1
Totally symmetric C-C Stretch Vibration: 995 cm-1
Elektronenkonfiguration Benzol
LUMO
HOMO
Absorption und Floureszenz: Benzol
925 cm-1
995 cm-1
Einstein Koeffizienten
Absorption
Fluoreszenz
|1
|1
hn
2
|1
hn
hn
|0
B01  01
Stimulierte
Emission
|0
A10  B01n
3
|0
B10  B01
Absorption
R
Schwingungsrelaxation
1-10 ps
R
Fluoreszenz
10 ns
R
n=1
Absorption:
FC  0
Emission:
FC  0
( S0 )

( S1 )
1
n=0
n=1
n=0
R
( S1 )

( S0 )
1
Benzol
925 cm-1
995 cm-1
Jablonski Diagram
schnell (Kasha‘s Rule)
kIVR
1-10 ps
2.Periode: langsam
Schwere Elemente: schnell
100ns
10ns
(dipolerlaubt)
200fs –100ns
Harmonische Potentialflächen
R2
R1
Photochemie: H2+-Molekül
eV 4
3
2
1
1
-1
-2
2
3
4 R/Å
Femtochemistry:
Ahmed Zewail, Nobel Prize 1999
Photodissociation of ICN
M. Dantus, M. J. Rosker, A. H. Zewail, J. Chem. Phys. 87 (1987) 2395
A. H. Zewail, J. Phys. Chem. A 104 (2000) 5660
Femtosecond Lasers
CPM Laser 1980
Pump-Probe Spectroscopy
Pump-Probe Spectroscopy
Pump-Probe Spectroscopy
Pump-Probe Spectroscopy
Prototype Photochemical Reaction: ICN
M. Dantus, M. J. Rosker, A. H. Zewail, J. Chem. Phys. 87 (1987) 2395
A. H. Zewail, J. Phys. Chem. A 104 (2000) 5660
probe
Photochemie: H2+-Molekül
eV 4
1
pump
2
1
-1
-2
probe
3
2
3
4 R/Å
Prototype Photochemical Reaction: ICN
M. Dantus, M. J. Rosker, A. H. Zewail, J. Chem. Phys. 87 (1987) 2395
A. H. Zewail, J. Phys. Chem. A 104 (2000) 5660
Prototype Photochemical Reaction: NaI
T. S. Rose, M. J. Rosker, A. H. Zewail, J. Chem. Phys. 91 (1989) 7415
A. H. Zewail, J. Phys. Chem. A 104 (2000) 5660
Electronic Photochemistry of HONO
hn
HONO  HO· + · NO
rN=O
S10
S
R2
R1
Cotting, Huber, JCP 195 (1996) 6208
rO-N
Photochemical Reaction: Conical
Intersection
S1 and S2 in pyrazine in the Q6a and Q10a subspace
Photochemical Reactions in Nature:
Isomerization of Rhodopsin
T. P. Sakmar, Curr. Opinion in Cell Biology 14 (2002) 189
Photochemical Reactions in Nature:
Isomerization of Rhodopsin
Q. Wang, R. W. Schoenlein, L. A. Peteanu, R. A. Mathies, C. V. Shank,
Science 266 (1994) 422
Photochemical Reaction: Conical
Intersection
S. Hahn, G. Stock, J. Phys. Chem. B, Vol. 104, 2000, 1146
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Rotationsspektrum von HCl
Rotationsspektroskopie
Trägheitsmoment:
I   mi xi2
i

xi : Abstand von der Drehachse,
welche durch Schwerpunkt geht
m1
m2
2-atomiges Molekül
I  R2
R
mit:
m1  m2

m1  m2
Rotationsspektroskopie
Drehimpuls
l  I
Energie

m1
m2
Erot
1 2 l2
 I 
2
2I
Korrespondenzprinzip
R

ˆ
l  l  i

Schrödingergleichung (in 2D)
 

  E
2
2I 
2
2
Korrespondenzprinzip
klassisch
Ort
x
Impuls
p
Drehimpuls
l
Energie
E
quantenmechanisch
xˆ  x  

pˆ   i 
x
ˆl   i  


ˆ
E  i  
t
Rotationsspektroskopie
Energiezustände
Entartung:
J=5: E=30B
11
J=4: E=20B
9
J=3: E=12B
7
J=2: E=6B
J=1: E=2B
J=0: E=0
5
3
1
Erot
2

J ( J  1)  BJ ( J  1)
2I
mit
J  0,1,2, 
mJ   J ,..., J
Auswahlregeln:
Permanentes Dipolmoment
DJ  1
DmJ  0,1
Rotationsspektrum von HCl
EJ  BJ ( J  1)
 EJ  EJ 1  2 BJ
Rotationsspektroskopie
Energiezustände
Entartung:
J=5: E=30B
11
J=4: E=20B
9
J=3: E=12B
7
J=2: E=6B
J=1: E=2B
J=0: E=0
5
3
1
Erot
2

J ( J  1)  BJ ( J  1)
2I
mit
J  0,1,2, 
mJ   J ,..., J
Auswahlregeln:
permanentes Dipolmoment
DJ  1
DmJ  0,1
Rotationsspektroskopie: mehratomige Moleküle
Molekül
Trägheitsellipsoid:
Linearer Kreisel:
m1
m2
m3
I  m x
HCN
2
i i
i
Erot  BJ ( J  1)
Auswahlregeln: Dipolmoment
DJ  1
DmJ  0,1
mit
J  0,1,2, 
mJ   J ,..., J
Rotationsspektroskopie: mehratomige Moleküle
Molekül
Trägheitsellipsoid:
Symmetrischer Kreisel:
oblate:
I||  I 
prolate:
I||  I 
m1
m2
m3
m3
m3
Benzol
Erot  BJ ( J  1)  ( A  B) K 2
mit
2
2
B
, A
2I 
2I||
Auswahlregeln: Dipolmoment
DJ  1 DK  0
DmJ  0,1
CH3Cl
J  0,1,2, 
K   J ,..., J
mJ   J ,..., J
Rotationsspektroskopie: mehratomige Moleküle
Molekül
Trägheitsellipsoid:
Sphärischer Kreisel:
m1
m2
m1
m1
CH4
m1
Erot  BJ ( J  1)
mit
2
B
2I
J  0,1,2, 
K   J ,..., J
mJ   J ,..., J
Auswahlregeln: Dipolmoment immer 0
DJ  1 DK  0
DmJ  0,1
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
Rotations-Schwingungsspektrum
von CO
J=4
n=1
J=3
J=2
J=1
J=0
Etot  Evib  Erot
1

   n    BJ ( J  1)
2

Auswahlregeln:
P-Zweig
R-Zweig
J=4
J=3
n=0
J=2
J=1
J=0
Übergangsdipolmoment
bezüglich Schwingung
D n  1
D J  1
CO2: Normalmoden
elektronische Spek.
Schwingungsspek.
vibronische Spek.
RotationsSchwingungsspek.
rovibronische Spek.
Rotationsspek.
S2
S1
DEel
DErot
Hˆ tot  Hˆ el  Hˆ vib  Hˆ rot
Etot  Eel  Evib  Erot
 tot   el   vib   rot
S0
DEvib
S2
S1
DEel
DErot
S0
Hˆ tot  Hˆ el  Hˆ vib  Hˆ rot
Eel  Evib  Erot
DEvib
Ende
Zeit:
Ort:
jeweils Dienstag 8-10, Mittwoch 10-12
34-K-01
Übungen:
• Mittwoch 10.15-12.00 (jede 2. Woche,
erstmals 3.Okt, 34K01 und 13K05)
• Abgabe jeweils am Dienstag davor, 12.00
• Übung obligatorisch, 10 min Quiz, zählt 20%
zur Endnote
Betreuer:
Steven Waldauer
Halina Strzalka
34 K 92
34 K 90
Raman Spektroskopie: Polarisierbarkeit
Polarisierbarkeit:
  
Hˆ  Hˆ (0)  Hˆ (1)  Hˆ (0)  exˆ  Hˆ (0)  
Vergleich Störungstheorie 1. und 2. Ordnung mit Taylorentwicklung
dEn
(0)
E n  En 
d
 En
(0)
1 d 2 En

2
2
d

 0
1
    2  ...
2
Störungstheorie 1.Ordnung:
En
(1)
  n (0)  n (0)
 2  ...
 0
Raman Spektroskopie: Polarisierbarkeit
  
Polarisierbarkeit:
Hˆ  Hˆ (0)  Hˆ (1)  Hˆ (0)  exˆ  Hˆ (0)  
Vergleich Störungstheorie 1. und 2. Ordnung mit Taylorentwicklung
dEn
(0)
E n  En 
d
 En
(0)
1 d 2 En

2
2
d

 0
 2  ...
 0
1
    2  ...
2
Störungstheorie 2.Ordnung:
En
( 2)

m n
n
( 0)
m
( 0)
n
E
( 0)
E
( 0)
m
2
2
n (1)  
mn
n (0)  m(0)
E
(0)
n
E
(0)
m

Beispiel: Polarisierbarkeit atomarer Wasserstoff
2 px
1s
1s  c2 px
+
Störungstheorie 2.Ordnung:
En
( 2)

m n
n
( 0)
m
( 0)
n
E
( 0)
E
( 0)
m
2
2
n (1)  
mn
n (0)  m(0)
E
(0)
n
E
(0)
m

Raman Spektroskopie: Polarisierbarkeit
Hˆ  Hˆ (0)  Hˆ (1)  Hˆ (0)  exˆ  Hˆ (0)  
Vergleich Störungstheorie 1. und 2. Ordnung mit Taylorentwicklung
dEn
(0)
E n  En 
d
 En
(0)
1 d 2 En

2
2
d

 0
 2  ...
 0
1
    2  ...
2
 Dipolmoment:
dE

  0  
d
Wasserstoff:
9
2
  a3