Frage:

Statistische Thermodynamik und Grenzfläche
1.
Grundlagen der statistischen Thermodynamik
1.1
1.2
1.3
2.
den
Phasenumwandlungen und chemisches Potential
Das chemische Potential einer Mischphase
Phasengleichgewichte
2.3.1 Phasengleichgewichte in Einkomponentensystemen
2.3.2 Phasengleichgewichte in Mehrkomponentensystemen
Oberflächenstrukturen von Festkörpern
Festkörperdynamik
Metalle und Halbleiter
Struktur und Dynamik von Flüssigkeiten
Grenzflächen
4.1
4.2
4.3
4.4
5.
aus
Festkörper und Flüssigkeiten
3.1
3.2
3.3
3.4
4.
Größen
Phasenumwandlungen von Mischungen
2.1
2.2
2.3
3.
Boltzmann-Verteilung
Molekulare Zustandssumme
Berechnung von thermodynamischen
Zustandssummen
Grenzfläche Flüssigkeit-Gas, Flüssigkeit-Flüssigkeit, FlüssigkeitFestkörper in nichtgeladenen Systemen
Grenzfläche Festkörper-Gas
Interionische Wechselwirkung in Elektrolytlösungen
Interionische Wechselwirkungen an Grenzflächen
Grenzfläche Elektronenleiter/Ionenleiter
5.1
5.2
Elektrochemie im Gleichgewicht
Kinetik von Elektrodenreaktionen
11
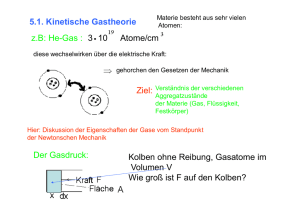
1. Grundlagen der statistischen Thermodynamik
Das Ziel der statistischen Thermodynamik ist die Beschreibung makroskopischer Eigenschaften von Stoffen aus den mikroskopischen Eigenschaften der
darin enthaltenen Atome und Moleküle. Die Quantenmechanik liefert uns die
Zustände und deren Energien. Das Verbindungsglied zwischen mikroskopischer
und makroskopischer Welt ist die temperaturabhängige Besetzung der
quantenmechanischen Zustände, die Boltzmann-Verteilung (hier kommt die
Statistik ins Spiel).
1.1 Die Boltzmann-Verteilung
Die Boltzmann-Verteilung gibt die temperaturabhängige Besetzung der
quantenmechanischen Zustände an.
Sie wird gebraucht:
für die Korrelation mikroskopischer und makroskopischer Eigenschaften
für die Spektroskopie: Übergänge nur möglich, wenn Besetzungsdifferenz
zur Berechnung von Gleichgewichten
zur Berechnung von Wärmekapazitäten
zur Berechnung von Reaktionsgeschwindigkeiten.
Frage:
N
ni
Wie viele Moleküle haben bei einer bestimmten Temperatur die
Energie 1, wie viele Moleküle bei dieser Temperatur die Energie
2 , usw....?
Gesamtzahl der Moleküle
Zahl der Moleküle mit Energie i (Besetzung)
∞
Eges = ∑ ε i n i
i
Beispiel: 4 Moleküle, harmonische Oszillatoren, Eges = 4hν.
Es gibt verschiedene Besetzungsmöglichkeiten bei fester Gesamtenergie:
1=0
2=hν
3=2hν
4=3hν
5=4hν
n1=N-1=3
n2=0
n3=0
n4=0
n5=1
n1=N-4=0
n2=4
n3=0
n4=0
n5=0
n1=N-2=2
n2=0
n3=2
n4=0
n5=0
n1=N-3=1
n2=2
n3=1
n4=0
n5=0
n1=N-2=2
n2=1
n3=0
n4=1
n5=0
Jede dieser Besetzungen hat ein eigenes statistisches Gewicht, das durch
die verschiedenen Aufteilungsmöglichkeiten auf die Moleküle zustande kommt.
21
Zum Beispiel hat die Besetzung in Zeile 1 oben 4 Anordnungsmöglichkeiten auf
die Moleküle, in Zeile 2 nur eine. Manche davon sind zum Teil äquivalent
(äquivalent ist zum Beispiel, wenn Molekül 1 und 2 oder 2 und 1 je im
Quantenzustand 1xhν sind)
W: Zahl der unterschiedlichen Anordnungs-/Kombinations-Möglichkeiten
W n 1 , n2 ,. .. =
N!
N !
n 1 ! n2 ! n 3 !
Gesamtzahl der Kombinationsmöglichkeiten
n1!n2!n3!... reduziert um die äquivalenten Kombinationen in einem
Energiezustand: z.B. können 2 Moleküle den gleichen
Quantenzustand besitzen.
Beachte: Wird ein Zustand der Energie i nicht besetzt, so ist ni = 0 also 0! = 1
Quantenzustände, die durch alle ihre Quantenzahlen unterschieden werden,
besitzen das Gewicht 1 (siehe Würfelspiel!)!
Berechne mit obiger Formel die Anordnungsmöglichkeiten W für obige Tabelle,
bzw. verifiziere dadurch die obige Formel.
1=0
n1=N-1=3
n1=N-4=0
n1=N-2=2
n1=N-3=1
n1=N-2=2
2=hν
n2=0
n2=4
n2=0
n2=2
n2=1
3=2hν
n3=0
n3=0
n3=2
n3=1
n3=0
4=3hν
n4=0
n4=0
n4=0
n4=0
n4=1
5=4hν
n5=1
n5=0
n5=0
n5=0
n5=0
W
4
1
6
12
12
Es stellt sich in einem Molekülensemble (~menge) immer die
Quantenzahlverteilung mit der höchsten Anordungsmöglichkeit ein. Diese ist
die Boltzmann-Verteilung. Sie entsteht durch die Mittelwertbildung der
Besetzungen unter Berücksichtigung der Anordnungsmöglichkeiten.
Motivation der Boltzmann-Formel:
Ein „Ensemble“ aus vier gleichen harmonischen Oszillatoren
1 = 0  h  
2 = 1  h  
3 = 2  h  
4 = 3  h  
5 = 4  h  
6 = 5  h  
Nebenbedingug t = 5  h  
ni ist Besetzungszahl der Energie i
Zahl N der Systeme ist 4
Es gibt die folgende Möglichkeit 5  h   mit Quantenzuständen zu erzeugen:
Energiewert in h   :
0, 1, 2, 3, 4, 5
Besetzungszahlen:
n1, n2, n3, n4, n5, n6
Energieverteilungen:
0, 3, 1, 0, 0, 0,
0x0 + 3x1 + 1x2 = 5, W = 4!3! = 4
31
6 = 5h
5 = 4h
 4 = 3h
3 = 2h
 2 = 1h
1 = 0h
W = 4 unterschiedliche Realisierungsmöglichkeiten
(Mikrozustände) des Makrozustandes 031000
{n1, n2, n3, n4, n5, n6}
1, 1, 2, 0, 0, 0,
1x0 + 1x1 + 2x2 = 5,
1, 2, 0, 1, 0, 0,
1x0 + 2x1 + 1x3 = 5,
2, 1, 0, 0, 1, 0,
2x0 + 1x1 + 1x4 = 5,
2, 0, 1, 1, 0, 0,
2x0 + 1x2 + 1x3 = 5,
1, 3, 1, 0, 0, 0,
1x0 + 3x1+1x2 = 5,
3, 0, 0, 0, 0, 1,
3x0 + 1x5 = 5,
n1
n2
n3
n4
n5
n5
W = 4!2! = 12
W = 4!2! = 12
W = 4!2! = 12
W = 4!2! = 12
W = 4!3! = 4
W = 4!3! = 4
W = 56
= (1x12 + 1x12 + 2x12 + 2x12 + 1x4 + 3x4)/56 = 1,5
= (1x12 + 2x12 + 1x12 + 0x12 + 3x4 + 0x4)/56 = 1,07
= (2x12 + 0x12 + 0x12 + 1x12 + 1x4 + 0x4)/56 = 0,71
N = ni
= (0x12 + 1x12 + 0x12 + 1x12 + 0x4 + 0x4)/56 = 0,43
= (0x12 + 0x12 + 1x12 + 0x12 + 0x4 + 0x4)/56 = 0,214
= (0x12 + 0x12 + 0x12 + 0x12 + 0x4 + 1x4)/56 = 0,07
Mittlere Besetzung in Abhängigkeit der Energie
41
Pi = ni/N
1,6
Nebenbedingung: E(total) = 5h
Pi=ni/N
mittlere Besetzung
1,4
Beachte die Besetzungswahrscheinlichkeit pi = ni/N
1,2
1,0
0,8
0,6
0,4
0,2
0,0
1
0
2
3
5
4
Energie in Quantenzahlen
Obige Kurve repräsentiert die wahrscheinlichste Besetzung (n*) der Energiezustände. Die
Besetzungswahrscheinlichkeit ergibt sich durch die Division durch die Anzahl der Teilchen (hier 4). Die
unterschiedliche Besetzung für die verschiedenen Quantenzustände resultieren aus der Nebenbedingung (hier E
= 5 h ). Man kann auch bei 4 Teilchen bereits den typischen exponentiellen Abfall der Besetzung mit der
Energie beobachten. Die (theoretische) Kurve hat noch einige Knickstellen und das Experiment kann bei 4
Teilchen noch nicht diese häufigste Verteilung annehmen (Besetzungen müssen ganzzahlig sein!).
Da wir mit sehr großen Teilchenzahlen arbeiten (1 Mol besitzt 6.0 x10 23 Teilchen) können wir sicher sein, dass
sich durch die gute Statistik die mathematisch bestimmte Verteilung mit dem größten statistischen Gewicht (W)
durchsetzt.
Die Boltzmannverteilung:
Version 1 für quantenmechanische Zustände
Pi =
− εi /kT
− ε i /kT
n¿i
=
N
e
∑e
− ε i / kT
=
e
Q ist die Zustandssumme
Q
i
Erklärung: Die Summe muss über alle Quantenzahlen durchgeführt werden. Oft
ist die Energie eines quantenmechanischen Zustandes nicht von allen
Quantenzahlen abhängig. Es ist dann günstiger über die Energien
(Energieniveaus) zu summieren. Der Informationsverlust (wie viele Zustände
haben gleiche Energie) muss in einen Entartungsfaktor gi eingearbeitet werden.
Version 2 für Energieniveaus
n
Pi=
i
N
− εi /kT
¿
=
gi e
− εi / kT
∑ gi e
− ε i /kT
g e
= i
Q
gi ist der Entartungsfaktor und Q wieder die
i
Zustandssumme
51
Für einfache Abschätzungen, ob ein Zustand bei einer Temperatur populiert ist
oder nicht, genügt die
Version 3: Für Besetzungsverhältnisse
pi ni
− Δε /kT
= = e ij
pj nj
Nun Wiederholung
Quantenmechanische Probleme und ihre Lösungen
H-Atom
harmonischer Oszillator/anharmonischer Oszillator
starrer Rotator
Teilchen im Kasten
Typische Energiewerte:
kT (300 K) ~ 200 cm-1
0,2 cm-1<B< 60 cm-1 (H2)
200 cm-1 <hvvib < 4000 cm-1
10 000 cm-1 < hvel < 106 cm-1, außer bei Atomen
in der Thermodynamik EKasten << 200 cm-1
Berechung einiger Besetzungen als Übungsaufgaben
Beispiel: Berechnung der Gleichgewichtskonstanten
Die Bedeutung der Zustandssumme, Beispiel Isomerisierung
n¿i
P =
=
Die Boltzmann-Verteilung i N
− εi /kT
− ε i /kT
e
∑e
− ε i / kT
=
e
Q
ist auf die Besetzung
i
aller quantenmechanischen Zustände anwendbar! Dabei sind die Zustände durch
ihre Quantenzahlen voneinander verschieden.
Sie gilt insbesondere auch für "kommunizierende" Systeme wie Konformere,
Isomere, Tautomere, die thermisch ineinander umgelagert werden können, so
dass eine Gleichgewichtsverteilung entsteht.
61
Isomer A
Energie(A)
0
Isomer B
11
7 (A)
9
6 (A)
7
5 (A)
5
4 (A)
3
3 (A)
2
2 (A)
Energie(B)
12
5 (B)
10
4 (B)
8
3 (B)
6
2 (B)
4
1 (B)
0

1 (A)
1
Beispiel: Ein Molekül hat zwei Isomere A und B. Ist die Barrierenhöhe mit kT
vergleichbar, so stellt sich nach einiger Zeit ein Gleichgewicht zwischen A und
B ein. Für die Gleichgewichtskonstante Keq gilt:
K eq=
[B ]
[A ]
Die Anzahl der Moleküle in den Schwingungszuständen in A i(A) und in B
i(B) lässt sich mit der Boltzmann-Verteilung berechnen.
[ A ] [B ] V = N ges= N ges ∑ pk = N ges
k
[ A ]⋅ V = ∑ n i A = N ges ∑ p i =
i
i
[B ]⋅ V = ∑ n j B =
N ges
−ε
e j
∑
Q ges j
[∑ p
i
N ges
∑ e− εi
Q ges i
i
A
∑
j
pj B
]
A /kT
und
j
B /kT
Beachte, dass beide Isomere auf den gemeinsamen niedrigsten Energiepunkt
bezogen sind!
e
Da aber ∑
i
− ε i A /kT
=Q A
e
und ∑j
− ε j B /kT
71
=Q B
folgt:
K eq=
[B ] Q B /V
=
[A ] Q A /V
bezogen auf einen Energienullpunkt.
Möchte man jedes Konformer auf seinen Grundzustand beziehen, so folgt mit
 = 1(B)-1(A)>0
[B ]
K eq=
=
[A ]
∑j e
− Δε ε j B ,0 /kT
Q A /V
¿V
= e− Δε/ kT
Q B ,0 /V
Q A /V
Allgemein gilt für die Gleichgewichtskonstante einer Reaktion AB  A + B
K eq=
[A ][B ] − Δε /kT Q A /V⋅ Q B /V
= e
[ AB ]
Q AB /V
mit  als Energieunterschied [1(A) + 1(B)] – 1(AB).
Diese Konzeption gilt allgemein auch für chemische Reaktionen. Beachte, dass
dort in den Atomen nur Translationen, aber im Molekül nun auch Vibrationen
und Rotationen möglich sind. Wir müssen für die Bestimmung von
Gleichgewichten bei chemischen Reaktionen also die Zustandssummen der
einzelnen Freiheitsgrade einsetzen.
1.2 Die molekulare Zustandssumme
− ε i /kT
Q≡ ∑ g i e
i
für T  0 Q = 1
für T   Q = 
− ε i /kT
Für i >> kT ist e
1 wenn 1 = 0; sonst 0, wenn i  0
bei unendlich vielen Zuständen mit
Beitrag 1. Alle Zustände sind gleich
wahrscheinlich (Würfeln ohne
Nebenbedingung)
klein!
Q ist also ein Maß für die Zahl von Zuständen, die bei der jeweiligen
Temperatur besetzt sind.
Die Zustandssumme spaltet sich auf in eine elektronische, eine vibratorische,
eine rotatorische, eine translatorische und eine Kernspin-Zustandssumme. Da
diese Freiheitsgrade unabhängig sind gilt:
81
Qges =QelQvibQrotQtransQnuc
Die Zustandssumme ist wichtig:
(i)
(ii)
da man aus ihr alle thermodynamischen Funktionen, die aus der PC II
bekannt sind, herleiten kann!
da man mit ihr Reaktionsgleichgewichte berechnen kann!
Die Zustandssumme der Translation Qtrans
Translationszustandssumme für eine eindimensionale Bewegung entlang der x Achse. Modellsystem: Teilchen im 1D-Kasten.
2
h
εx n =
8 ma
x
n = 1,2,3,… Quantenzahlen
2
n2 h2
8ma 2 kT
−
∞
n2
Qx= ∑ e
x
n= 1
∞
∫
e−
y
2
dn
1
mit ax als der Strecke, entlang der sich das Teilchen frei bewegt.
Substitution:
2 2
n h
= y2
8ma 2 kT
2
Abl.
x
dn=
h 2ndn
= 2y d y
8ma 2 kT
x
2 ydy⋅ 8 ma 2 kT
x
2
h 2n
y
n2 h 2
8ma 2 kT
dn=
dn=
1/2
8ma 2 kT⋅ 2
x
x
d y
2nh2
8 ma 2 kT
x
2
h
1/2
d y
Aus der Formelsammlung:
91
∞
∫
π
2
2
e − y d y=
0
∞
Q x = ∫ e− y
0
2
≃ Integration von 0  
dn

8ma 2 kT
x
h2
8 ma
Q x=
x2
2
kT
1/2
π
2
h
d y
Q x=
2π ma 2 kT
h
1/2
x
2
Da Bewegungen in x,y und z voneinander unabhängig folgt:
2π⋅ mkT
h3
Qtrans = Qx  Qy  Qz =
3/2
⋅ a x a y az
V
2π⋅ mkT
h3
Qtrans =
3/2
⋅V
(es ist oft vorteilhaft V nicht explizit einzusetzten)
Die Zustandssumme der Rotation Qrot
∞
Qrot = ∑ g rot e
− ε J /kT
J= 0
−
ℏ2
J J 1
2 IkT
−
ℏ2
J J 1
2 I kT
∞
= ∑ 2J 1 e
J= 0
∞
∫
Qrot =
2J 1 ⋅ e
y
dJ
J= 0
dy=
2 I kT
Qrot =
ℏ2
ℏ2
2J 1 dJ
2 I kT
∞
∫
e− y dy
y= 0
0− − 1 = 1
Q rot=
8π 2 I kT
σh2
σ= 2 H2
σ = 1 HD Entartung durch Kernspin
Die Zustandssumme der Schwingung
101
(einschließlich Nullpunkts-Energieniveau, die z.B. bei einer unimolekularen
Dissoziation verfügbar wird):
−
Q vib= ∑ g vib e
v
Summe
hυ
1
v
kT
2
h/kT = x
1
Integral, da die h-Abstände zu groß sind.
1
2
−x v
Q vib= ∑ e
e-x
v
3
2
−x v
e − x Q vib = ∑ e
v
Für die Differenz dieser beiden Terme folgt:
− x
−3x
2
Q vib 1− e− x = e 2 − e
e
−3 x
2
v= 0
−
x
2
−
hυ
2 kT
=e
x
−
2
Q vib=
e
e
=
−x
−
1− e
1− e
−e
−5 x
2
v= 1
e
−5 x
2
−e
−7 x
2
.. .. .
v= 2
hυ
kT
Ohne Nullpunktsniveau:
Q vib= 1− e
−
hυ − 1
kT
Für 3N – 6 Schwingungen folgt:
3N− 6
Q vib=
∏
i= 1
−
¿
e
hυi
2 kT
1− e
−
hυ i
kT
¿
Die elektronische Zustandssumme
Beispiel: Fluor-Atom Der Grundzustand hat die Gesamtdrehimpulsquantenzahl
J=3/2, also Entartung 4 (EJ=3/2:=0). Der angeregte Zustand bei 400 cm-1 hat die
Gesamtdrehimpulsquantenzahl J=1/2, also Entartung 2.
111
− ε 1 /kT
− ε2 /kT
Qel = g 1 e
g2 e
. .. ..
− ε 2 /kT
−0
hier Qel = 4 e 2 e
. .. . .
Bemerkungen:
Für Jod muß bei Raumtemperatur der angeregte Zustand nicht berücksichtigt
werden (Eso = 7741 cm-1) jedoch aber die Entartung des Grundzustandes (!).
Bei der Dissoziation I2  I + I spielt diese Entartung eine wichtige Rolle für die
Gleichgewichtskonstante (siehe Kap. 4.2).
Die Entartung des Grundzustandes ist auch für Moleküle möglich: Für O 2 3
folgt: S=1, also Entartung des Grundzustandes 2S+1=3.
1.3
Berechnung von thermodynamischen Größen aus den
Zustandssummen
Für die innere Energie U=E eines thermodynamischen Systems gilt:
E=
∑ ni ε i =
i
E=
N
Q
∑ εi e
i
− ßε i
N
∂
−
e
∑
Q i
∂ß
E= −
− εi / k T
Annahme: gi = 1 für alle Zustände
mit ß = 1/kT
N ∂Q
∂ ln Q
=− N
Q ∂ß
∂ß
∂ ln Q ∂ ln Q
∂ T ∂ ln Q
=
=k
∂ß
1
1 ∂T
∂
∂
kT
T

Nebenrechnung:
∂T
1
∂
T
∂

1
T
∂T
=
∂ T −1
=−T −2
∂T
und somit
∂T
=−T2
1
∂
T
∂ ln Q
∂ ln Q
= − kT 2
∂β
∂T
E =+ NkT 2
∂ ln Q
∂T
V
Mittlere Energie von N Teilchen (wichtig!)
E entspricht der inneren Energie U der Thermodynamik, wenn Q alle
Freiheitsgrade der Bewegung des Teilchens einschließt (einschließlich
Nullpunktszustand).
121
Innere Energie und Wärmekapazität
Die innere Energie eines molekularen Gases besteht aus Translations-,
Rotations- und Schwingungsenergie. Wie aus Übungsblatt 1 folgt, sind viele
Translations und Rotationszustände besetzt (beachte, dass selbst die Rotationen
bei tiefen Temperaturen „ausfrieren“ können, siehe Zeichnung cv gegen T). Sie
stehen bei Raumtemperatur voll zum Energiespeichern zur Verfügung.
∂U
f
Allgemein gilt ∂ T V = c V = 2 R
mit f = Anzahl der Freiheitsgrade wobei f für Schwingungen doppelt zählt
(Merkregel: da es Ekin und Epot gibt).
Umgekehrt kann U als Integral über cv nach dT bestimmt werden (z.B. wenn
cv(T) als Meßkurve vorliegt, dann U=Fläche darunter)!
Die Anzahl der Freiheitsgrade in einem Molekül mit N Atomen ist immer 3N.
Davon sind
3 Translationen, 2 Rotationen und 3N-5 Vibrationen für lineare Moleküle
3 Translationen, 3 Rotationen und 3N-6 Vibrationen für nichtlineare Moleküle
Da zum Beispiel im Festkörper die Schwingungsfrequenzen der drei
Raumrichtungen niedrige Energien besitzen (folglich bei 300 K besetzt;
Schwingungen im Festkörper heißen Phononen: kollektive Schwingungen mit
6
großem m) folgt c V = 2 R= 3R (Gesetz von Dulong-Petit)
Frage: Warum zählen die Schwingungsfreiheitsgrade doppelt?
Zunächst: Mittlere Schwingungsenergie eines 2-atomigen Moleküls aus
Zustandssumme (eines harmonischen Oszillators).
E= NkT 2
∂ ln Q
∂T
V
e− hυ/2kT
Q=
1− e− hυ/kT
V = konstantes Volumen
E vib= NkT 2
[ {
∂
e− hυ/2kT
ln
∂T
1− e − hυ/ kT
}]
V
a
ln = ln a− ln b
b
131
E vib= NkT 2
∂
hυ
−
− ln 1− e− hυ /kT
∂T
2 kT
[ {
}]
V
∂
1
ln f x =
⋅ f' x
∂x
f x
E vib = NkT 2
[
−
hυ
−
2 kT 2
−e
hυ
kT
¿
hυ
kT 2
1− e− hυ /kT
−
V
hυ
kT
N⋅ hυ⋅ e
1− e− hυ/kT
1
E vib= Nh υ
2
]
∣
¿e
¿e
hν/kT
hυ / kT
∣
:n
Zahl der Mole
'
Schwingungsenergie pro Mol E vib :
E' vib=
1
N hυ
2 A
N A⋅ hυ
e hυ/kT − 1
1
klassisch
Klassisch gilt für 2 Freiheitsgrade E vib = 2⋅ 2 kT= kT pro Molekül und RT pro
Mol.
Beispiel: Wärmekapazität von O2 , hier nur Schwingungsanteil!
Exper. cvib = 0,03R (bei 300K); klassisch cvib = R für 1 mol Gas.
Bei 300K ist nur bei einem kleinen Teil der O2-Moleküle die Schwingung
angeregt, so dass nur wenig Energie in der O2-Schwingung gespeichert werden
kann.
∂ E vib
c vib =
∂T
∂
= N A⋅ hυ
∂
T
V
− e hυ/kT⋅−
c vib= N A⋅ hυ
hυ
kT 2
e hυ/kT − 1
2
hυ
kT
−1
u ' u ' v − v' u
=
v
v2
e −1
hυ
= R⋅
kT
N A⋅ k
2
e hυ/kT
e hυ/kT − 1
Schwingungsfrequenz von O2:  = 4,671013s-1
141
2
2
J
6,626⋅ 10− 34 J⋅ s⋅ 4,67⋅ 10 13 s− 1
ea
c vib= 8,314
⋅
K⋅ mol 1,38⋅ 10− 23 JK− 1⋅ 300K
e a− 1
2
a
a = 7,4705
cvib = 0,031 R
in Übereinstimmung mit dem Experiment.
Nun zum Grenzübergang „Exponent“ gegen Null:
dieser Fall tritt ein für T gegen  (Molekül bei hohen Temperaturen) oder
hν gegen 0 (Festkörper)
Mit
θ=
h⋅ υ
k
charakteristische Temperatur
folgt
c vib= R⋅
θ
T
2
θ
T
e θ /T⋅ e − θ /T
2
e θ /T − 1 ⋅ e− θ /T
= R⋅
2
2
1− e− θ /T ⋅ e θ/T
Nebenrechnung:
2
e θ /T − 1 ⋅ e− θ/T = e θ /T⋅ e θ /T⋅ e− θ/T − 2 e θ /T e− θ/T e − θ /T
= e θ/T 1− e− θ/T
2
0
Für T   ist cvib wegen 0 unbestimmt.

Verfahren nach de l’Hospital:
f x
f' x
f n x
lim
= lim
= ¿⋅ ¿lim n
g x x a g' x
g x
x a
x a
(siehe Übung)
Zähler und Nenner sind für sich so lange zu differenzieren, bis einer von
beiden oder beide nicht mehr Null oder Unendlich ergeben.
lim c vib=
R
Dies ist der klassische Wert von cvib. Analoges folgt für den Grenzübergang hν
gegen 0. Also es gilt: Schwingungen zählen doppelt, wenn sie besetzt sind. Im
T
∞
151
Falle einer teilweisen Besetzung kann man nun den exakten Beitrag mit der
Zustandssumme berechnen (siehe oben).
Beispiel: Berechung der Entropie
Die Entropieänderung gibt die Richtung eines irreversiblen Prozesses an.
ΔS>0
ΔS=0
A ⇋ B
A  B
<
Der Zustand mit möglichst großer Entropie S (Entropie von System und
Umgebung) wird angestrebt.
Statistik:
Zustand mit größter Zahl unterschiedlicher Konfigurationen
(größter Wahrscheinlichkeit W) wird angestrebt.
Daher
S
Entropie
¿¿¿= f W ¿
¿
Die Entropien der Einzelsysteme addieren sich z.B. bei Vereinigung der
Gasvolumina gleicher Teilchen.
S1,2 = S1 + S2 = f(W1) + f(W2)
Gesamtwahrscheinlichkeiten sind Produkte der Einzelwahrscheinlichkeiten
W = W1 · W2
Also
S1,2 = f(W) = f(W1·W2) = f(W1) + f(W2)
Das gilt nur, wenn
S = k · lnW
lnW1·W2 = lnW1 + lnW2
(ohne Beweis: Die Proportionalitätskonstante k ist die Boltzmann-Konstante.)
161
Die Entropie ist also ein Maß für die Wahrscheinlichkeit eines Zustandes (Zahl
seiner Realisierungsmöglichkeiten ≙ Konfigurationen). Mit zunehmender
Unordnung nimmt die Zahl der Realisierungsmöglichkeiten zu.
Entropie ≙ Maß für die Unordnung.
2.Hauptsatz der Thermodynamik: In einem abgeschlossenen System führt jeder
irreversible Prozess zu einer Zunahme der Unordnung.
Volumenabhängigkeit der Entropie
N
In jedem kleinen Volumenelement Ve seien V V e Moleküle enthalten, die nicht
unterscheidbar sind.
W T=
N!
{
V
N⋅ e !
V
V /V e
}
T = konstante Temperatur
V
V
V
V
N⋅ e⋅ ln N⋅ e − N⋅ e
Ve
V
V
V
V
ln W T = N⋅ ln N − N ln N − N⋅ ln e
V
ln W T = N⋅ lnV − N ln V e
ln W T = N⋅ ln N − N −
Das statistische Gewicht wächst also mit dem Volumen.
S T = k⋅ N ln V − k⋅ N ⋅ ln V e
n⋅ R
da Ve eine Konstante ist, ist ihre Ableitung null.
n⋅ R
dST = n  RdlnV
Nach Integration kann aus der Volumenänderung die Entropieänderung berechnet werden
Temperaturabhängigkeit der Entropie
S V = k⋅ ln W = k⋅ N⋅ ln N − ∑ n j ln n j
[
j
]
siehe Kapitelanfang: Stirlingsche Näherung von lnW
S V = k⋅ N⋅ ln N − k⋅ N ∑
j
e− ε /kT
N⋅ e − ε /kT
¿ln
QV
QV
j
j
n j/ N
171
S V = k⋅ N⋅ ln N − k⋅ N ∑
j
e− ε /kT
¿ ln N ln e− ε /kT − ln Q V
QV
S V = k⋅ N⋅ ln N − k⋅ N⋅ ln N
S V = k⋅ N⋅ ln Q V
N
T
[
j
∑ ε j⋅ e
j
k⋅ N ∑
j
ε j e − ε /kT
⋅
kT
QV
]
j
k⋅ N⋅ ln Q V
− ε j / kT
beachte:
QV
∑
j
e − ε /kT
=1
Q
j
Mit der inneren Energie U
∑ ε j⋅ e
U = N⋅
− ε j /kT
QV
j ist die Energie des Zustandes j einschließlich Nullpunktsenergie.
folgt
S V = k⋅ N⋅ ln Q V
U
T
als Grundgleichung zur Berechnung der Entropie aus den Zustandsummen Q
und inneren Energien U der verschiedenen Freiheitsgrade (vgl. Übungen).
Für die Temperaturabhängigkeit der Entropie gilt dann
dSV
=
dT
k⋅ N⋅
dlnQ V
dT
1 ∂U
T ∂T
−
V
U
T2
2
U/T vgl. Kapitalanfang
Ableitung nach Quotientenregel
dSV
dT
=
1 ∂U
T ∂T
dSV = C V dln T/K
V
CV
T/K bezeichnet die Höhe der Temperatur ohne Einheit.
S V = C V ln T/K
const .
Mit zunehmender Temperatur steigt die Entropie.
Wenn sich gleichzeitig Volumen und Temperatur ändern, kann jeder für
konstantes Volumen gültige Mikrozustand mit jedem für konstante Temperatur
gültigen kombinieren:
181

W = WT · WV
lnW = lnWT + lnWV
S = n R lnV + n · cV · lnT + const.
dS = n · R d lnV + n · cV · d lnT
1.5
Berechnung der Geschwindigkeitsverteilung bzw.
Energieverteilung von Gasmolekulen: Die Maxwellver
teilung
Allgemein gilt:
p ε=
g ε e− ε/kT
Q
oder für endlich genaue Messgenauigkeit in Intervallen d:
p ε dε=
g ε e− ε/kT
dε
Q
Dabei ist p()d der Anteil aller Teilchen mit Energien zwischen  und +d.
Natürlich gilt für die Summe aller Anteile:
∑
i
∞
p ε i dε = ∫ p ε dε= 1
0
3/2
2π mkT
V
Qtrans ist bekannt Q= h 2
Es fehlt die Entartung g(εi) für die Translation "Teilchen im Kasten".
Für die Energie im dreidimensionalen Topf mit dem Volumen V = L3 gilt:
ε nx , n y , nz =
h2
n 2x n2y n2z
2
8 mL
Es stellt sich die Frage wie man die Entartung berechnen kann. Dabei ist zu
beachten, dass wegen der großen Töpfe die Energieabstände sehr, sehr klein
gegen kden die Quantenzahlen n sehr groß.
Zunächst erinnert x2 + y2 + z2 = R2 an eine Kugelgleichung (R = Radius). Die
Energie lässt sich also auch durch das Quadrat von R ausdrücken:
h2 R2
h2 R2
ε nx , n y , nz = ε R =
=
8 mL2
8 mV 2/ 3
Da die Quantenzahlen positiv sind, kann man die Entartung der Energie als alle
Vektoren mit Länge R finden.
Im "Quantenzahlraum":
191
Im Bereich der Vektorlänge 4 (R) und 4,5 (R + R) liegen folgende Zustände:
42 = 16 und 4,52 = 20,25
(4,1,1), (1,4,1), (1,1,4), (3,3,1), (3,1,3), (1,3,3), (2,2,3), (2,3,2), (3,2,2)
In der Orangenschale R = 4 und R+ΔR = 4,5 befinden sich alle Quantenzustände
h2 16
h 2 20 , 25
ε
=
ε
Δε=
die im Energieintervall zwischen
8 mL2 und
8 mL2
mit
R 2=
liegen.
8 mV 2 /3 ε
gilt zunächst für das Volumen  eines Quadranten im
h2
Qantenzahlraum
4 /3 πR 3 πR 3 π 8 mV 2 /3 ε
Φ=
=
=
2
8
6
6
h
3/2
=
π 8mε
6 h2
3/2
V
Die "Orangenschale", also die Entartung, berechnet sich als:
∂Φ
π 8m
g ε dε = Φ ε Δε − Φ ε =
dε =
∂ε
6 h2
− ε i /kT
Q= ∑ g ε i e
Für Q folgt:
Letztlich
Q=
2π mkT
h2
∞
=
i
folgt
3/2
V
für
∫
mit
3/2 ε
1 /2
π 8m
V dε =
4 h2
3/2
ε 1/2 Vd ε
g ε e− ε/kT dε , da
0
p(ε)
3/2
der
translatorischen
π 8m
und der Entartung zur Energie  g ε dε= 4 h2
201
Zustandssumme
3 /2
ε 1 /2 V⋅ dε :
p ε dε=
π 8m
4 h2
3/2
ε 1/2 V⋅ e− ε/kT dε
2π mkT
h2
3/2
V
π 4
=
4 π kT
3/2
ε 1/2 e− ε/kT dε
Die Verteilung der Translationsenergie (nach Maxwell):
Durch Integration von a bis  folgt für die Wahrscheinlichkeit ein Teilchen mit
einer Energie Ea zu treffen: p ε a ε ∞ =
2 ε a − ε a /kT
e
. Man kann nun für eine
π kT
Reaktion, die exo-energetisch oder mit Barriere abläuft, berechnen wie viele
Teilchen überhaupt in der Lage sind eine solche Reaktion einzugehen.
211
Beachte die Ähnlichkeit mit dem Strahlungsgesetz nach Planck (Photonen
im 3D-Kasten mit Länge L, Bedingung L = n·λ, E=hν, Entartung macht
Anstieg, e-hν/kT macht Abfall).
Die Maxwell-Geschwindigkeitsverteilung
1 2
∂ε
nun ist ε = 2 mv also ∂ v = mv
π 4
4 π kT
3/2
π 4m
=
4 π kT
3 /2
p v dv=
=
2
m
⋅ v⋅ e− mv /2kT⋅ mv⋅ dv
2
1 2 − mv2 /2kT
⋅v⋅e
⋅ dv
2
3/2
π⋅ 2⋅ 2⋅ 2 m
2⋅ 2 2 π kT
p v dv= π⋅ 4
m
2π kT
und ∂ ε= mv⋅ ∂ v nun:
2
⋅ v 2⋅ e− mv
3/2
⋅ v 2⋅ e− mv
2
/2 kT
⋅ dv
/2 kT
⋅ dv
(Maxwell-Geschwindigkeitsverteilung)
Beachte, dass aus
∞
∫
p v dv= 1= π⋅ 4
0
m
2π kT
3/2 ∞
⋅ ∫ v 2⋅ e − mv
2
/2kT
⋅ dv
0
folgt:
∞
∫
0
v 2⋅ e− mv
2
/2kT
⋅ dv =
π kT
2 m
3/2
Der Mittelwert der Geschwindigkeit ist:
221
∞
v=
∫
0
m
v ⋅ 4π
2π kT
3/2
−
v 2⋅ e
m v2
2kT
⋅ d v = . .. .. .. . ..
Mit Hilfe der Integraltafel erhält man
8RT
Teilchen: v= π M .
Beispiel für v [m/s] bei 25C:
H2
He
Ar
Cl2
Hg
Cs
v=
8k T
π m
und daraus für 1 mol
1770 m/s
1256 m/s
398 m/s
298 m/s
177 m/s
351 m/s (500C)
Bemerkung: Die Schallgeschwindigkeit c hängt mit
zusammen und c  v .
v
direkt proportional
Berechnet man den Mittelwert von v2 , so erhält man: ⟨v 2⟩= 3 kT /m= 3 RT / M
Dies steht in bester Übereinstimmung mit der PCII:
3
1
kT= E kin= m v 2
2
2
Setzt man die 1.Ableitung der Verteilungsfunktion gleich Null, so erhält man:
v wahrsch. =
2 kT
m
1 /2
=
2RT
M
1/2
merke:
v
[ ]
m
s
=
T /K
145 . 51
v wahrsch . : v :
M
=
2512. 48 / M
(bei 25°C)
v 2 = 1 : 1. 12 : 1 . 26 (unabhängig von T!)
Die Geschwindigkeiten sind nicht gleich, da die Verteilungsfunktionen nicht
symmetrisch sind.
Analog zur dreidimensionalen Geschwindigkeitsverteilung (MaxwellGeschwindigkeitsverteilung) ergibt sich für die eindimensionale
Geschwindigkeitsverteilung
231
n∗ v x , v x Δv x
N
m
dv x =
2πk T
mv
1/2
⋅e
−
x
2
2kT
⋅ dv x
auch Boltzmann-Geschwindigeitsverteilung genannt
Setzt man die 1.Ableitung der Verteilungsfunktion nach v gleich Null, so erhält
man:
v wahrsch. =
v
2RT
M
[m/s] bei 25C:
1/2
H2
He
Ar
Cl2
Hg
Cs
1770
1256
398
298
177
351 (500C)
merke:
v wahrsch. : v :
⟨v 2⟩ = 1 : 1 .12 : 1 . 26
Die Geschwindigkeiten sind nicht gleich, da die Verteilungsfunktionen nicht
symmetrisch sind.
241
Messung der Geschwindigkeit
Blendenversatz
Flugzeit zwischen den rotierenden Blenden:  = L / v.
Der Strahldurchtritt erfolgt, wenn:
Hier: Erklärung des Überschallstrahls!
251
L/v = d/u
Anhang: Herleitung der Boltzmann-Verteilung:
Die Konfiguration mit größtem Gewicht bekommt man, indem man den
Maximalwert der Funktion W (oder ln W, da die Funktion monoton ist!) über
das Verschwinden der Ableitung sucht.
Nebenbedingung: Erhaltung der Gesamtenergie E und der Gesamtmolekülzahl N des Systems
∑ n i εi =
E
d ln W =
∑i
∑ ni= N
i
i
d E= 0= d
∂ ln W
∂ ni
d N = 0=
d ni
∑ d ni
i
∑ n i εi = ∑ εi d n i
i
i
Berücksichtigung der Nebenbedíngungen:
d ln W =
∑i
∂ ln W
∂ ni
d ln W =
∂ ln W
∂ ni
d ni
α
∑i d ni − β ∑i εi d ni
α − β εi
∑
{¿} d n i = 0
i
, : Lagrangesche Multiplikatoren
Stirlingsche Näherung:
ln
x! ≈ x
ln
x− x
für große x
261
¿ ln
N ! / n1 ! n2 !
¿ ln N ! − ln n1 ! n 2 !
ln W
∑ ln n j !
j
N − N − ∑ n j ln n j −
j
N ln N − ∑ n j ln n j
¿ ln N ! −
¿
N ln
¿
nj
j
∂ n j ln n j
∂ ln W
≈ −∑
∂ ni
∂ ni
j
{
¿− ∑
j
{
}
∂ nj
∂ ln n j
ln n j n j
∂ ni
∂ ni
= δi
j
¿− {ln n i
}
1}
Mit
ln ni  1
folgt
− ln n¿i
n¿
i = e
mit
¿
ni
α − β εi = 0
α− β ε
i
als der wahrscheinlichsten Besetzung.
 = ?
N=
∑ n ¿i = ∑ e α e
i
N
i
− β εi
n
i¿
− β εi
=
e
− β εi
∑e
Boltzmann-Verteilung
i
∑e
i
− β εi
= molekulare Zustandssumme Q
271
!
∂ ln x
1
=
!
∂ x
x
 = ?
Der Mittelwert einer Größe x
x=
∑
i
n xi
i¿
N
kann über die Boltzmannstatistik berechnet und mit dem Mittelwert x aus der
phänomenologischen Thermodynamik verglichen werden.
Daraus erhält man:
β=
1
k T
bzw.
n
i
N
− ε i /kT
¿
=
− ε / kT
gi e
− εi / kT
∑ gi e
g e i
= i
Q
i
gi = Entartung von Zustand i
(z.B. gJ = 2J + 1 bei starrem Rotator)
ni e− ε i /kT
−
= − ε /kT = e
n0 e 0
Δεi
εi − ε 0 / kT
n0 = Zahl der Moleküle im Nullpunktszustand
(Zustand mit tiefster Energie)
281