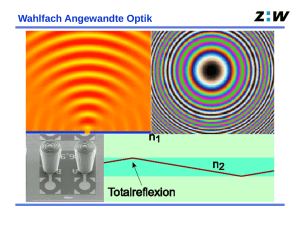
Geometrische Optik
Werbung
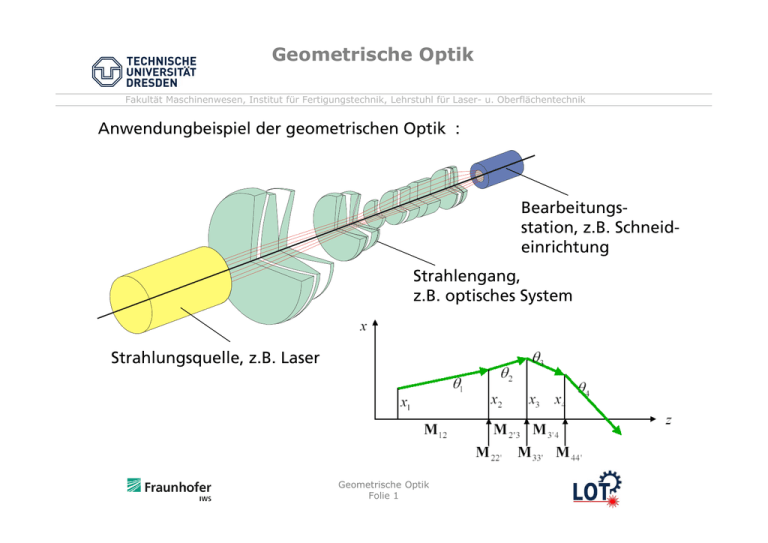
Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungbeispiel der geometrischen Optik : Bearbeitungsstation, z.B. Schneideinrichtung Strahlengang, z.B. optisches System Strahlungsquelle, z.B. Laser Geometrische Optik Folie 1 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Die geometrische Optik oder Strahlenoptik betrachtet elektromagnetische Wellen im sichtbaren Bereich des Spektrums elektromagnetischer Wellen, das Licht. Sie beschreibt die Wechselwirkung von Licht mit Objekten, deren Abmessungen wesentlich größer sind als die Wellenlänge von Licht. FIR 100 NIR 10-2 V I S 10-4 UV 10-6 VUV XR 10-8 FIR NIR VIS UV VUV XR far infrared, fernes Infrarot near infrared, nahes Infrarot visible, sichtbarer Bereich Ultraviolett Vakuum-UV X-ray, Röntgenstrahlen cm Die geometrische Optik ist eine makroskopische Betrachtungsweise; sie genügt um die Funktionsweise von (licht)optischen Instrumenten zu beschreiben. Das Licht wird idealisiert betrachtet: die Wellen- oder Teilchennatur des Lichtes wird vernachlässigt. Die Strahlenoptik gestattet keine Beschreibung der Beeinflußung von Objekten, die mit Licht in Wechselwirkung standen. Geometrische Optik Folie 2 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Die geometrische oder Strahlenoptik folgt Vereinfachungen und dem Fermatschen Prinzip : - - Pierre de Fermat 1601 - 1665 Licht kann durch einzelne Strahlen oder Strahlenbündel beschrieben werden. Ein Strahl beschreibt im homogenen Medium eine gerade, beliebig dünne, Linie, die sich geradlinig, im inhomogenen Medium gekrümmt ausbildet. Die Ausbreitungsgeschwindigkeit des Lichts hängt vom Medium ab. Strahlen stehen senkrecht auf den Phasenflächen eines entsprechenden Wellenmodells. Die Richtung der Strahlen ist umkehrbar. Licht legt zwischen einem Ausgangs- und Endpunkt den Weg zurück, für dessen Überbrückung ein Zeitextremum erforderlich ist. Der Verlauf von Lichtstrahlen ist unabhängig voneinander; Strahlen können sich schneiden, es gilt das Überlagerungs- o. Superpositionsprinzip. Wellenoptik Λ 0 geometrische Optik Geometrische Optik Folie 3 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Geometrische Optik : Wechselwirkung von Licht mit Objekten, damit auch mit Komponenten optischer Systeme, deren Abmessungen wesentlich größer sind als die Wellenlänge von Licht. Beugungs- und Interferenzeffekte sind nicht beschreibbar und werden vernachlässigt : Translation : Reflektion : Brechung (Dispersion) : Einfallslot einfallender Strahl optische Achse Einfallslot einfallender Strahl reflektierter Strahl einfallender Strahl Einfallwinkel Reflexionswinkel Einfallwinkel Grenzfläche Grenzfläche optisches System Brechungswinkel Durchgang von Strahlen Richtungsänderung eines in paraxialer Näherung Strahls durch Umlenkung Geometrische Optik Folie 4 gebrochener Strahl Richtungsänderung eines Strahls durch veränderte Geschwindigkeit Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Reflexion : Brechung : y y P1´(x1´,y1´) P1(x1,y1) ´ s1 0 P1(x1,y1) s1´ P(x,0) Grenzfläche s1 0 x P(x,0) Grenzfläche x s2 P2(x2,y2) sin ´ sin Einfallwinkel = Reflexionswinkel = n2 n1 = const. Snelliussches Brechungsgesetz Quelle : Stoppe, H. Physik Geometrische Optik Folie 5 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Brechung : Nach dem Fermatschen Prinzip ist der Brechungsindex das Verhältnis der Geschwindigkeiten von Licht in beiden Medien : sin sin = n2 n1 = c1 c2 Üblich ist ein Bezug des Brechungsindex auf die Lichtgeschwindigkeit im Vakuum : c0/c1 n = c0/c2 Unter den Bedingungen der geometrischen Optik für optisch transparente Medien. Vakuum Luft Eis Wasser menschl. Auge Ethanol Plexiglas Kronglas Quarz Steinsalz Flintglas Rubin Glas Geometrische Optik Folie 6 1,0 1,00029 1,31 1,33 1,35..1,42 1,37 1,49 1,51 1,54 1,54 1,60 1,76 1,5-1,9 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Abhängigkeit der Wechselwirkungen Absorption, Reflexion und Transmission (A + R + T = 1) von der Wellenlänge; hier Beschränkung auf die Transmission: am Beispiel von Glas mit einem Brechungsindex n = 1,472: Geometrische Optik Folie 7 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Sonderfälle von Reflexion und Brechung : diffuse Reflexion (Streuung) : Totalreflexion : Einfallslot diffuse Strahlung Grenzfläche Grenzfläche Einfallswinkel einfallender Strahl Einfallswinkel < Brechnungswinkel für = (Grenzwinkel) : sin = Geometrische Optik Folie 8 1 n Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Beispiel zur Totalreflexion : Transmission Reflexion Geometrische Optik Folie 9 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Beispiel der Totalreflexion : Strahlengang in Prismenfeldstechern : Grenzwinkel : Wasser/Luft Glas/Luft Kronglas/Luft 48° 45° 42° Quelle : Zeller/Franke Geometrische Optik Folie 10 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Reflexion : ebener Spiegel : gekrümmter Spiegel : konkav konvex ebener Spiegel Gegenstand sphärischer Spiegel Teil einer Kugelfäche Bild Parallelstrahl Brennpunktstrahl g Gegenstandsweite P´ b Bildweite Scheitelpunkt S O P ´ M Krümmungsmittelpunkt F O optische Achse f Brennweite r Krümmungsradius Quelle : Stoppe, H. Physik Geometrische Optik Folie 11 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Reflexion : Kaustik am Hohlspiegel Gegenstand O Parallelstrahl P Brennpunktstrahl M Q Parallelstrahl Q´ Bild F P´ f Parabolspiegel b g Brennweite Krümmungsradius r Bildweite Gegenstandsweite r 1 1 1 Abbildung : + = 2 g b f b PQ β = P´Q´ = - g Quelle : Stoppe, H. Physik Brennweite : f Maßstab : S Scheitelpunkt O optische Achse Geometrische Optik Folie 12 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Reflexion : Kaustik am Hohlspiegel Parabolspiegel Die sphärisch reflektierten Beispiel der ‘klassischen‘ Kaustik, Lichtstrahlen bilden eine sog. hervorgerufen an der Innenseite Kardioide (Herzkurve) eines polierten Hohlzylinders Geometrische Optik Folie 13 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Ausbreitungsgeschwindigkeit des Lichtes : Ausbreitungsgeschwindigkeit : n = n () cn = cn () Darstellung anhand der optischen Dispersion am Prisma : brechender Winkel Ablenkungswinkel Gegenstand 2 Einfallwinkel O Brechungsindex : n = Ausfallwinkel Q sin min sin 2 2 Ablenkungswinkel : min = (n -1) ne–1 mittlere Dispersion : e = n – n F C Quelle : Stoppe, H. Physik Geometrische Optik Folie 14 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Ausbreitungsgeschwindigkeit des Lichtes : dn d Dispersion : = Hauptbrechzahl o. Abbesche Zahl : ne–1 e = n – n F C Linie C D E F G H K mit n = n (), cn = cn () n d ... n F Brechungsindizes für Spektrallinien nach Fraunhofer ne ( = 546,1 nm) Farbe [nm] rot 643.8469 orange 609,7234 grün 546.0740 blaugrün 479.9914 blau 435.8343 violett 407.8453 violett 403.5642 n() 1,615 1,619 1,623 1,636 1,642 1,649 1,652 [°] 47,8 48,2 48,6 49,9 50,5 51,2 51,5 Angaben für Flintglas DF 621362 Quelle : Schröder, G. Technische Optik Geometrische Optik Folie 15 Geometrische Optik Hauptbrechzahl-Dispersion-Diagramm (Abbe-Diagramm) für optische Gläser Geometrische Optik Folie 16 Quelle : Schröder, G. Technische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Quelle : Schröder, G. Technische Optik Beispiele : Geometrische Optik Folie 17 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : sphärische, dünne Linsen, t « r, r´ : Hauptstrahl Parallelstrahl Gegenstand Brennweite : P r Brennpunktstrahl Abbildung : 1 = 1 + 1 f r´ Q´ O optische Q M F Achse F´ f 1 1 1 = (n-1) + f r r´ M´ Bild f´ g b O b PQ Maßstab : = =- g P´Q´ P´ g Gegenstandsweite b t Bildweite bikonvex/konkav plankonvex/konkav konvex~konkav Quelle : Stoppe, H. Physik Geometrische Optik Folie 18 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : brechender Winkel O Ablenkungswinkel r´ r M P Q g M´ Krümmungsmittelpunkt b Krümmungsradius Gegenstandsweite Brennweite : optische Achse O P´ Q´ Bildweite 1 1 1 = (n-1) f r + r´ Abbildung : 1 = 1 + 1 f g b Maßstab : b PQ = = β P´Q´ g Quelle : Stoppe, H. Physik Geometrische Optik Folie 19 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Linsensysteme : 3-Linsensystem 2-Linsensystem 1-Linsensystem Quelle : Buran GmbH Hohenwarsleben 2011 Geometrische Optik Folie 20 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Abbildungsfehler : brechender Winkel O Ablenkungswinkel M M´ optische Achse O P´ Farblängenfehler einer für 2 Wellenlängenbereiche für 3 Wellenlängenbereich bikonvexen Sammellinse korrigierte Farblängenfehler korrigierte Farblängenfehler eines achromat. Linsensystems eines apochrom. Linsensystems Quelle : Buran GmbH Hohenwarsleben 2011 Geometrische Optik Folie 21 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : sphärische, dicke Linsen : n Gegenstand nL allgemeiner Fall : n = nL = n´ n´ Objektbrennweite : 1 (nL-n´) (nL-n) (nL-n)(nL-n´) t = nr´ - nr nnL f rr´ P r´ r Bildbrennweite : F´ O Q MF optische Achse S H K K´ H´ f M´ S´ O b t f´ = - n´ f n Abbildung : f´ g Gegenstandsweite Q´ P´ Bildweite Bild 1= f f´ + g b Maßstab : = b n´ nn Quelle : Stoppe, H. Physik Geometrische Optik Folie 22 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : Beschreibung von sphärischen, dicken Linsen mit einem Satz von sechs Kardinalpunkten auf der optischen Achse : - erster und zweiter Brennpunkt (Fokus), - erster und zweiter Hauptpunkt, - erster und zweiter Knotenpunkt. ein vor Eintritt in das System achsenparalleler Strahl schneidet die optische Achse nach dem System im zweiten Brennpunkt; ein in umgekehrter Richtung durchlaufender, achsenparalleler Strahl schneidet die optische Achse vor dem System im ersten Brennpunkt : P F´ Q F S H f H´ Q´ S´ f´ P´ Geometrische Optik Folie 23 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : ein in das System eintretender, achsenparalleler Strahl und ein resultierender, das System verlassender Strahl wird vorwärts bzw. rückwärts fortgeschrieben, beide schneiden sich in einem Punkt; die Menge der Schnittpunkte für alle Achsenabstände der eintretenden Strahlen bilden die zweite Hauptebene; der Schnittpunkt der zweiten Hauptebene mit der optischen Achse ist der zweite Hauptpunkt : Hauptpunkte H und H´ Bestimmung der Hauptpunkte H und H´per Messung und Bezug zum Linsenscheitel Geometrische Optik Folie 24 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : ein auf den ersten Knotenpunkt gerichteter (i. a. schiefer) Strahl verlässt das System unter demselben Winkel vom zweiten Knotenpunkt ausgehend : Knotenpunkte K und K´ für paraxiale Strahlen sind sie die Hauptebenen sphärische Flächen, senkrecht zur optischen Achse durch die Hauptpunkte, ist der Brechungsindex des Mediums auf beiden Seiten außerhalb des Systems gleich, (z. B. Luft), dann sind die Knotenpunkte identisch mit den Hauptpunkten; die Abstände zwischen Hauptpunkten und Brennpunkten vor und nach dem System sind gleich. Geometrische Optik Folie 25 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : P sphärische, dünne Linsen, t « r, r´ : Q´ Q sog. „Linsenmacherformel“ : 1 1 1 + = r r´ f F f nL -1 n f´ F´ P´ P F´ dicke Linsen : Q F S H H´ n t 1 1 1 1- n + = r r´ f´ r r´ L n´ f´ = f n S´ f´ f sog. „Linsenmacherformel“ : Q´ nL n -1 P´ Problem : von welchem Punkt aus werden die Brennweiten f und f´ angetragen ? Geometrische Optik Folie 26 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Brechung : y P1(x1,y1) Parallelstrahl Brennpunktstrahl Mittelpunktstrahl Mittelpunktstrahl Brennpunktstrahl Parallelstrahl P(x,0) s1 0 Grenzfläche s2 O x F O Optisches Banksystem : P2(x2,y2) sin sin = n2 n1 = const. Snelliussches Brechungsgesetz Quelle : Stoppe, H. Physik; Dr. Martin Henschke Gerätebau Geometrische Optik Folie 27 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Optisches System : Komponenten sind hauptsächlich dünne und dicke Linsen zusammengesetzte Linsen, ebene, sphärische oder parabolische Spiegel und Prismen. Die Komponenten bilden eine gemeinsame optische Achse; die Auslegung eines optischen Systems kann auf der Annahme der paraxialen Näherung und der Gesetzmäßigkeiten der geometrischen Optik basieren : Beispiel : zwei dünne Linsen im Abstand e, Gesamtbrennweite f* : f* = ff´ f + f´ - e bei e « f + f´ Geometrische Optik Folie 28 1 1 1 = + f* f f´ Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Konventionen des Matrixformalismus: 1. 2. 3. 4. 5. 6. Die Strahlrichtung läuft von links nach rechts, in positiver Richtung der z-Achse. Der Radius einer konvexen Fläche ist positiv, R > 0, derjenige einer konkaven Fläche negativ, R < 0. Die Steigung ist positiv, wenn sich der Strahl von der Achse entfernt, negativ, wenn er sich darauf zubewegt. Eine Gegenstand- oder Bildweite ist positiv (negativ), wenn sie vor (hinter) dem abbildenden Element liegt. Gegenstandsgrößen werden oberhalb (unterhalb) der z-Achse positiv (negativ) gezählt. Reflektive Optik wird behandelt, indem der Strahlengang nach jedem Element umgeklappt wird. Quelle : Meschede Optik, Licht und Laser Geometrische Optik Folie 29 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Ausbreitung von Kugelwellen im Matrixformalismus: Paraxiale Näherung: sin σ ≈ tan σ ≈ σ R= x σ Quelle : Pedrotti Optik für Ingenieure Geometrische Optik Folie 30 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik paraxiale Näherung : ~ sin ~ tan 3,000 Bogenmaß, Sinusfkt., Tangensfkt. Strahlwinkel gegenüber der opt. Achse 3,500 2,500 2,000 1,500 1,000 0,500 0,000 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 Winkel [°] Geometrische Optik Folie 31 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Translation : Durchgang durch ein homogenes Medium Brechung (Dispersion) : Brechung an einer sphärischen Fläche Geometrische Optik Folie 32 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Reflektion : Reflektion an einer sphärischen Fläche Geometrische Optik Folie 33 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Anwendungsfälle der Translation, Brechung : sphärische, dicke Linsen : Geometrische Optik Folie 34 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Beispiel der Ermittlung von Strahlverläufen : 50 sphärische, dicke Linse : hE = 10 mm E = 10° paraxiale Näherung Bogenmaß : 10° = 0,1745 hA = 10,9614 mm A = 0,089° ~ 44 10 10° R 450 0,089° R 300 Geometrische Optik Folie 35 10,9614 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Spezialfälle der Systemmatrix : Geometrische Optik Folie 36 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik ABCD Matrizen für einige optische Grundelemente. Aus: Technische Optik: Laser TU Braunschweig 2004 Geometrische Optik Folie 37 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Zusammenhang zwischen einer gewöhnlichen Kugelwelle, R(z), und einem Gaußschen Strahl, q(z) : Quelle : Pedrotti Optik für Ingenieure Geometrische Optik Folie 38 Geometrische Optik Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Aus: Optik, Licht und Laser, Kap.1, D. Meschede c 1999 B. G. Teubner Stuttgart Leipzig Geometrische Optik Folie 39 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Phasenfronten 0 r I Rz zR L z 0 Krümmungsradius der Phasenfront: 2 z R R z z 1 z Rayleighlänge: zR r0 2 Geometrische Optik Folie 40 Fernfelddivergenz: 0 r0 tan 0 0 r0 zR Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Strahltaille 2r0 2r Linse Fokus 2r(z0) 2rf z Laser zR L z0 f z=0 hemifokaler Resonator mit L = 500 mm Festkörperlaser mit = 1μm Geometrische Optik Folie 41 z0 = 7000 mm f = 1000 mm rf = 0,1 mm Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Geometrische Optik Folie 42 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Größe der Taille L g1g2 1 g1g2 r0 g1 g2 2g1g2 g 1 1 1 2 2 R Krümmungsradius der Spiegel R(z) Krümmung der Phasenfront L Resonatorlänge R L R r0 R(z) L Geometrische Optik Folie 43 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Da “reine Moden” in der Praxis selten vorkommen, wird ein Strahlpropagationsfaktor K (= Strahlqualitätskennzahl, Modenordnung) eingeführt. 2/ 1 r K: 00 00 r0 0 r0 0 b2 b Beugungsmaßzahl 0 < K 1 (K=1 beugungsbegrenzt) damit gilt: r0 r02 zR 0 1 z 2 2 r z r0 1 K zR Anstelle von K wird gelegentlich auch die Größe M² zur Strahlqualitätsdefinition verwendet. Im Rahmen der für die Praxis relevanten Genauigkeit kann für die meisten Laser die Umrechnung K 1/M² verwendet werden. Geometrische Optik Folie 44 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Beispiel einer industriellen Bikonvexlinse: Geometrische Optik Folie 45 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Beispiel einer industriellen Kollimationsund Fokussiereinheit Kollimationseinheit Fokussiereinheit Geometrische Optik Folie 46 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik TEMm,n TEM00 TEM10 Moden höherer Ordnung Falls der Spiegelradius a1, a2 (oder ein entsprechender Blendenradius) größer ist als der Grundmoderadius r00 , treten Moden höherer Ordnung auf : a) Rechtecksymmetrie TEM m,n Intensitätsverteilung wird durch Gauß-HermitePolynome beschrieben Hm,n Hermite-Polynome m,n Zahl der Knoten in x, y - Richtung m,n = 0,1,2 b) Rotationssymmetrie TEM p,l Intensitätsverteilung wird durch Gauß-LaguerrePolynome beschrieben L p,l Laguerre-Polynome p,l Zahl der Knoten in x, y - Richtung p,l = 0,1,2 Geometrische Optik Folie 47 Resonatorkenngrößen Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik Laguerre‘sche Moden (Rotationssymmetrie) Strahlradius : r0 r00 TEM00 b p=0 I=0 Strahldivergenz : 0 00 TEM00 b p=1 I=1 p=2 I=2 Benennung : TEM p,l p=3 I=3 Beispiel : TEM 01 p=4 I=4 b 2p l 1 Geometrische Optik Folie 48 Anfahrt Fraunhofer IWS Dresden Fakultät Maschinenwesen, Institut für Fertigungstechnik, Lehrstuhl für Laser- u. Oberflächentechnik