Ausgewählte Kapitel der Physik
Werbung
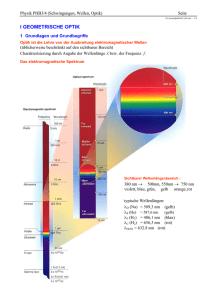
Ausgewählte Kapitel der Physik Optik Geometrische Optik 13.04.2015 Optik • • • • • • • Lichtstrahlen Schatten Reflexion Brechung -----------Polarisation Strahlengang in optischen Geräten 13.04.2015 Optik • Lichtstrahlen Sind divergent, konvergent oder diffus • Schatten Gelten als Beweis für die gradlinige Ausbreitung von Licht Punktförmige Quelle: Kernschatten Ausgedehnte Quelle: Halbschatten und Kernschatten. Was ist Licht? Lichtquanten? Wie schnell fliegen sie? Seit 1983 gilt c0 =299792458 m/s universelle Konstante, unabhängig von der Farbe der Strahlung (= Frequenz). c ist in allen Medien kleiner als im Vakuum. 13.04.2015 Optik • Schatten Bilder aus Bergmann-Schäfer, LB d. Experimentalphysik Bd. 3, Optik Finden Sie Anwendungsbeispiele zu den dargestellten Situationen H..Halbschatten, 13.04.2015 S…Kernschatten , W…Projektionswand Optik • Reflexion • Alle Winkel werden zum Lot gemessen • Einfallender Strahl, Lot und reflektierter Strahl liegen in einer Ebene • Einfallswinkel des Strahls = Ausfallswinkel des Strahls 13.04.2015 Optik • Ebener Spiegel • • • Der ebene Spiegel erzeugt virtuelle = scheinbare Bilder Die Bilder liegen symmetrisch zum Gegenstand scheinbar auf der Hinterseite des Spiegels. • Man hat den Eindruck, dass die Bilder von einem Punkt hinter dem Spiegel kommen. • (Welche Eigenschaften muss ein Spiegel haben, damit er gut spiegelt? ) 13.04.2015 Optik • Ebener Spiegel Mit zwei Spiegeln lassen sich sogar mehrere Bilder eines Gegenstandes erzeugen, da sich auch das virtuelle Bild im zweiten um den Winkel a dazu gekippten Spiegel ebenfalls spiegelt. Ordnet man drei Siegel in Form eines auf der Spitze stehenden Würfels, so erhält man einen Reflektor, der Strahlen aus beliebiger Richtung wieder dorthin reflektiert. (Kfz-Rückstrahler, Spiegel am Mond zur Entfernungsmessung ) 90°-Winkel-Spiegel 2-dimensional 13.04.2015 Optik • Hohlspiegel (konkav, cave= Höhle) • • Hohlspiegel kugelig: „Sphärische Spiegel“ Hohlspiegel paraboloid: „Parabolspiegel“ • Parallel zur optischen Achse einfallende Strahlen werden im Brennpunkt gesammelt • Scheitel (S)– Brennpunkt (F) = Brennweite f • (F) liegt in der Mitte zwischen (M) und (S) • Bei sphärischen Spiegeln gehen nur die achsennahen Parallelstrahlen durch den Brennpunkt (Katakaustik) 13.04.2015 Optik • Hohlspiegel (konkav, cave= Höhle) • Die Gleichungen gelten nur für achsennahe Strahlen • • Reelle Bilder sind stets verkehrt Virtuelle Bilder sind aufrecht • Reelle Bilder können auf einem Schirm aufgefangen werden, virtuelle nicht • • Spiegelteleskope verwenden Hohlspiegel Scheinwerfer positionieren die Lichtquelle im Brennpunkt Parallelstrahlbündel Für konvexe Spiegel gelten ebenso die Reflexionsregeln, allerdings sind Bilder, die hinter dem Spiegel entstehen stets virtuell, aufrecht und verkleinert. 13.04.2015 Optik Reflexion und Brechung nach dem Prinzip von Fermat 13.04.2015 Konstruktion des Strahlengangs: Die Kathete s des Dreiecks OAC bzw. OBC ist für beide die Selbe s = n1*sin(a) = n2*sin(b) Daraus folgt unmittelbar das Brechungsgesetz von Snellius. In der Demonstration erkennt man, dass neben der Brechung auch ein Teil des Strahls nach dem Reflexionsgesetz a = a‘ an der Grenzfläche reflektiert wird. Optik Brechungsgesetz von Snellius Beachte: Der Brechungsindex n oder die Lichtgeschwindigkeit c im Material sind zusätzlich abhängig von der Farbe des Lichts. Unterschiedliche Farben (=Wellenlängen) werden unterschiedlich gebrochen. Weiße Lichtstrahlen laufen nach einer Brechung i.A. auseinander. = Dispersion. 13.04.2015 Optik Lichtbrechung beim Übergang zwischen unterschiedlichen Medien in Zahlen: c0 = Lichtges c hwindigkeit im Vak uum Brec hzahl Brec hzahl Luf t /Vak uum W as ser/Vakuum Brec hungs gesetz n 1 = 1 .00 02 7 n 2 = 1 .33 Luf t ==> W ass er gegeben ist der Einf allswinkel a = 4 5° parallel zur Grenzf läc he 13.04.2015 a = 9 0° c1 = c2 = 1 0 0 c0 n1 c0 n2 8m = 2 .99 8 1 0 8m = 2 .99 7 1 0 8m = 2 .25 4 1 0 n 1 si n( a) s s n 2 si n( b ) n1 b = asi n si n( a) = 3 2.1 27° n2 n1 b = asi n si n( a) = 4 8.7 71° n2 s Optik Grenzwinkel der Totalreflexion Die Weg des Lichtstrahls kann auch in der umgekehrten Richtung durchlaufen werden: Der Strahl kommt aus dem optisch dichteren Medium zur Oberfläche und wird vom Lot weg gebrochen. Wenn der Auftreffwinkel a (alle Winkel werden zum Lot hin gemessen) klein genug ist, wird der Strahl teilweise reflektiert und teilweise durchgelassen. (grüner Strahl) Bei einem sehr großen Winkel kann der Strahl nicht mehr durchtreten, er wird vollständig reflektiert! (roter Strahlengang) Jener Einfallswinkel, bei dem gerade kein Strahl mehr durchkommt, weil er längs der Grenzschicht weiterläuft, heißt Grenzwinkel der Totalreflexion. sin(aG)= n2/n1 Bemerkenswert, aber erst mit dem Wellenbild verständlich, ist jener Einfallswinkel, bei dem reflektierter Strahl und gebrochener Strahl aufeinander senkrecht stehen. Die beiden Strahlen sind dann polarisiert, der reflektierte schwingt parallel zur Grenzfläche, der gebrochene senkrecht dazu. Ist der einfallende Strahl schon linear polarisiert, gibt es keine Reflexion in dieser Richtung (siehe Abb. Bergmann-Schäfer, LB. der Experimentalphysik). Der nach Brewster benannte Polarisationswinkel ist von der Brechzahl der betreffenden Farbe abhängig gemäß: tan(ap) = n2,1 . 13.04.2015 Brechung im Wellenbild Eine andere Erklärung für die Brechung folgt aus der unterschiedlichen Geschwindigkeit der Wellenausbreitung in den einzelnen Medien. Nach Huygens wird jeder von der Wellen zum Mitschwingen angeregte Ort zum Ausgangspunkt einer eigenen Elementarwelle. Diese bilden in ihrer Gesamtheit die Wellenfronten. Lichtstrahlen stehen senkrecht auf den Wellen-Fronten. Eine langsamere Ausbreitung im angrenzenden Medium führt zu einer Annäherung an die Senkrechte, b ist kleiner als der Einfallswinkel a. 13.04.2015 Optik Optik Grenzwinkel der Totalreflexion Ein spezieller Fall liegt vor, wenn der Übergang von einem Material zum anderen allmählich erfolgt. Der Lichtstrahl wird in kleinen Schritten „gebrochen“ . Der Brechungsindex ändert sich nicht schlagartig an einer Grenzfläche, sondern graduell. Solche Fälle liegen bei GradientenindexLichtwellenleitern vor. 13.04.2015 Optik Aus dem Grenzwinkel der Totalreflexion leitet man den Öffnungswinkel des Kegels für die Aufnahme von Lichtstrahlen an der Stirnfläche des LWL ab. Numerische Apertur „NA“. 13.04.2015 Optik • LWL-Herstellung bei Fa. Alcatel 13.04.2015 Optik LWL-Herstellung mit „Chemical Vapour Deposition“ (CVD) 13.04.2015 Optik • LWL-Herstellung bei Fa. Alcatel 13.04.2015 Optik • LWL-Herstellung bei Fa. Alcatel (1992) 13.04.2015 Optik 13.04.2015 Optik • Dispersion der Strahlen mit verschiedenen Wellenlängen Der Brechungsindex ist keine Konstante, er hängt u.A. von der Wellenlänge ab. Unterschiedliche Farben (bzw. Wellenlängen) werden unterschiedlich abgelenkt. Bei „normaler Dispersion“, hat Violett den größeren Brechungsindex, es wird daher am stärker gebrochen, Rot dagegen am wenigsten. Die Farben des ursprünglich weißen Strahls laufen unterschiedlich schnell, ein weißer Rechteckpuls läuft auseinander. 13.04.2015 Optik Dispersion der Strahlen mit verschiedenen Wegen im LWL Besonders bei den StufenindexFasern kann man unterschiedliche Wegstrecken im Strahlenbild erkennen. Die Strahlenbündel werden Moden genannt. Der maximale Unterschied in der Laufzeit tritt auf, wenn der mittlere, gerade Strahl und der extremste Zick-Zack Strahlengang betrachtet wird. (Größenordnung: ns / km) Der Zeitunterschied Dt = (nK-nM)*L/c0 wird mit zunehmender Faserlänge immer größer. Die Stufenindexfaser ist für den Signaltransport über große Längen schlechter geeignet als beispielsweise eine Gradientenindex-Faser. Wird der LWL bis auf die Größenordnung der Wellenlänge verkleinert, so bleibt letztlich nur die mittlere Mode erhalten „Monomode-Faser“ (ca.5µm Durchm.) 13.04.2015 Optik • Dispersion Rechteckige Lichtimpulse, die in Folge zunehmender Dispersionsbeiträge ineinander laufen. Enger aneinander liegende Impulse werden stärker verwischt. 13.04.2015