Volltext

Fakultät für Naturwissenschaft
Spezialisierungspraktikum
Optimierte irreversible Thermodynamik:
Modell einer stochastischen Wärmekraftmaschine
Karsten Leonhardt
Chemnitz, den 11. August 2009
Betreuer:
Prof. Dr. Karl Heinz Hoffmann
Inhaltsverzeichnis
1 Einleitung
5
2 Theoretische Grundlagen
2.1 Thermodynamik . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Zustand, Gleichgewicht und Zustandsänderungen
2.1.2 Wärme . . . . . . . . . . . . . . . . . . . . . . . .
2.1.3 Arbeit . . . . . . . . . . . . . . . . . . . . . . . .
2.1.4 Die Haupsätze . . . . . . . . . . . . . . . . . . . .
2.1.5 Kreisprozess . . . . . . . . . . . . . . . . . . . . .
2.1.6 Endoreversible Thermodynamik . . . . . . . . . .
2.2 Brownsche Bewegung . . . . . . . . . . . . . . . . . . . .
2.2.1 Langevin-Gleichung . . . . . . . . . . . . . . . . .
2.2.2 Langevin-Gleichung in einem Kraftfeld . . . . . .
2.2.3 Fokker-Planck-Gleichung . . . . . . . . . . . . . .
3 Durchführung
3.1 Modell einer stochastische Wärmekraftmaschine .
3.1.1 Isotherme Zustandsänderungen . . . . . .
3.1.2 Adiabatische Zustandsänderungen . . . . .
3.1.3 Konstruktion des Prozesses . . . . . . . .
3.1.4 Wirkungsgrad und maximale Leistung . .
3.2 Ein Kolloid in einem harmonischem Potential . .
3.2.1 Herleitung der Differentialgleichung für die
3.2.2 Maximierung der Arbeit des Kreisprozess .
3.2.3 Berechnung des Wirkungsgrades . . . . . .
3.2.4 Maximale Leistung . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
7
7
7
7
8
8
9
10
11
11
11
12
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
Varianz des Teilchenorts
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
15
15
16
18
18
20
24
24
28
32
33
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Zusammenfassung und Ausblick
37
Literaturverzeichnis
39
3
Inhaltsverzeichnis
4
1 Einleitung
Für die Entwicklung von Verbrennungsmotoren und anderen Wärmekraftmaschinen war
die im 19.Jahrhundert enstandene klassische Thermodynamik sehr entscheidend gewesen.
Um überhaupt solche Maschinen konstruieren zu können war es nötig,thermodynamische
Systeme zu definieren und herauszufinden, welche Größen diese Systeme charakterisieren.
Heute kann jeder mit dem Begriff Temperatur etwas anfangen, jedoch werden im allgemeinen Sprachgebrauch Begriffe wie Temperatur und Wärme oft vermischt. Gerade die
strenge Definition von Zustandsgrößen thermodynamischer Systeme und die Hauptsätze
der Thermodynamik sind die Grundlage vieler technischen Anwendungen. Im Laufe des
letzten Jahrhunderts konnten Ingenieure immer bessere Wärmekraftmaschinen bauen und
ihre Kenndaten wie z.Bsp. der Wirkungsgrad näherten sich den theoretischen Grenzen,
die aus der klassischen Thermodynamik bekannt sind, immer mehr an. Dennoch blieb
lange Zeit eine Lücke zwischen theoretischen und realen Werten. Die Lücke konnte durch
die Entwicklung der irreversiblen Thermodynamik weitgehend geschlossen werden. Man
wusste schon nach der Entwicklung der klassischen Thermodynamik, dass reale Prozesse nie
vollständig die theoretischen Werte erreichen werden. Jedoch brauchte die Entwicklung der
irreversiblen bzw. endoreversiblen Thermodynamik ihre Zeit und sie ist auch heute noch
ein großes Forschungsgebiet. Im Laufe des letzten Jahrhunderts wurden neben makroskopischen Systemen auch mikroskopische Systeme, wie sie u.a. in der Biologie auftreten, immer
interresanter. Bei mikroskopischen Systemen spielen aber oft thermische Fluktuationen eine
Rolle. Deswegen kann die Thermodynamik makroskopischer Systeme nicht ohne weiteres auf
mikroskopische Systeme übertragen werden. Man braucht zur Beschreibung mikroskopischer
Prozesse die Theorie der stochastischen Prozesse. Kann man auf den Grundgleichungen
stochastischer Prozesse thermodynamische Größen sinnvoll definieren? Mit dieser Frage
beschäftigten sich viele Forscher und es konnte das Konzept der stochastischen Thermodynamik entwickelt werden. Eine grundlegende Arbeit schrieb Ken Sekimoto mit [10] in
der er auf der Langevin-Gleichung innere Energie, Wärme und Arbeit definiert. In dieser
Arbeit wird das Modell einer stochastischen Wärmekraftmaschine vorgestellt, dass bereits
in [6] ausgearbeitet wurde. Wir wollen hier aber für alle Hauptresultate die Rechnungen
angeben und die Ergebnisse diskutieren.
5
1 Einleitung
6
2 Theoretische Grundlagen
2.1 Thermodynamik
In der klassischen Thermodynamik[3] ist ein thermodynamisches System ein makroskopisches
System das aus sehr vielen Elementargebilden (Atomen, Elektronen, Photonen, ...) aufgebaut
ist. Somit besitzt das System sehr viele Freiheitsgrade.
2.1.1 Zustand, Gleichgewicht und Zustandsänderungen
Zur Charakterisierung thermodynamischer Systeme dienen makroskopische Observablen,
die sogenannten Zustandsgrößen. Diese Zustandsgrößen sind Observablen, die in einem
physikalischem Experiment gemessen werden können. Man unterscheidet zwei Arten von
Zustandsgrößen.
Extensive Zustandsgrößen sind mengenproportional, d.h. sie verhalten sich additiv bei
der Zusammensetzung von Systemen. Beispiele dafür sind das Volumen V , die Masse m.
Intensive Zustandsgrößen sind dagegen mengenunabhängig. Die Temperatur T und der
Druck p sind intensive Zustandsgrößen.
Ein thermodynamisches System befindet sich im Gleichgewicht, wenn sich die Basis Zustandsgrößen zeitlich nicht mehr ändern. Erfahrungsgemäß strebt jedes abgeschlossene
System von allein in einen Gleichgewichtszustand. Ein abgeschlossenes System tauscht
weder Energie noch Teilchen mit der Umgebung aus und geht auch keine Wechselwirkung
mit äußeren Feldern ein.
Eine Zustandsänderung ist eine Folge von Zuständen, die das System durchläuft. Man
nennt eine Zustandsänderung quasistatisch, wenn sie nur aus einer Folge von Gleichgewichtszuständen besteht. Weiterhin unterscheidet man zwischen reversiblen und irreversiblen
Zustandsänderungen. Eine Zustandsänderung ist reversibel, wenn es sich um eine umkehrbare Folge von Gleichgewichtszuständen handelt, d.h., wenn bei zeitlicher Umkehr
der äußeren Bedingungen eine zeitliche Umkehr der vom System durchlaufenen Zustände
einhergeht. Bei einer irreversiblen Zustandsänderung folgt bei zeitlicher Umkehr der
äußeren Bedingungen nicht die zeitliche Umkehr der vom System durchlaufenen Zustände.
2.1.2 Wärme
Erfahrungsgemäß kann man an einem thermodynamischen System die Temperatur ändern,
ohne Arbeit zu leisten. Aus diesen Erfahrungen postuliert man Wärme als eine eigenständige
Energieform. Wenn wir annehmen das die Wärme wie jede andere Energieform eine extensive
7
2 Theoretische Grundlagen
Variable ist, dann können wir für die Wärmeenergie Ew schreiben:
dEw = T dS
(2.1)
Gl.(2.1) besagt, dass sich die Änderung der Wärmeenergie zusammensetzt aus einer intensiven Größe T und der Änderung einer extensiven Größe dS. Die intensive Größe T kann mit
der im Nullten Haupsatz postulierten intensiven Größe Temperatur identifiziert werden.
Die extensive Größe S ist die Entropie, die die entscheidende Größe für die Unterscheidung
von irreversiblen und reversiblen Zustandsänderungen ist. Für die Änderung der Wärme
∆Q gibt es eine Vorzeichenkonvention:
(
> 0, Wärme wird in das System hineingepumpt
∆Q =
< 0, Wärme wird aus dem System herausgepumpt
(2.2)
2.1.3 Arbeit
Die Arbeit wird definiert wie in der klassischen Mechanik und durch sie kann die Energie
eines Systems verändert werden. Die differentielle quasistatische Arbeit lässt sich schreiben
als:
m
X
δW =
Qi dqi
(2.3)
i=1
Dabei sind die q1 , . . . , qm die generalisierten Koordinaten und die Q1 , . . . , Qm die generalisierten Kraftkomponenten. Anstatt dW wird der Ausdruck δW benutzt, da es sich bei der
differentiellen Arbeit nicht um ein totales Differential handelt [7]. Auch für die Änderung
der Arbeit gibt es eine Vorzeichenkonvention:
(
> 0, am System geleistete Arbeit
∆W =
< 0, vom System geleistete Arbeit
(2.4)
2.1.4 Die Haupsätze
Nullter Haupsatz
Jedes makroskopische System besitzt eine intensive Zustandsgröße, die Temperatur T , die
in einem sich selbst überlassenen, abgeschlossenen System überall denselben Wert annimmt.
Dabei ist die Temperatur T eine skalare Meßgröße. Sind zwei thermodynamische Systeme
in thermischem Kontakt, dann hat die Temperatur der beiden Systeme im Gleichgewicht
denselben Wert.
8
2.1 Thermodynamik
Erster Haupsatz
Es wird eine neue Zustandsvariable eingeführt, die innere Energie U , die den gesamten
Energieinhalt des Systems darstellt. Da Energie weder gewonnen werden noch verloren
gehen kann, muss dU ein totales Differential sein. In einem Kreisprozess gilt also:
I
dU = 0
(2.5)
Der Erste Hauptsatz ist also nichts anderes als der Energieerhaltungssatz. Man kann den
Ersten Hauptsatz nun für verschiedene Systeme anwenden. Für ein offenes System, das
heißt es ist Teilchen-, Arbeits- und Wärmeaustausch erlaubt, gilt:
dU = δQ + δW + δEc
(2.6)
mit δQ Wärmeaustauschkontakt, δW Arbeitsaustauschkontakt und δEc Teilchenaustauschkontakt. Die “δ” weißen darauf hin, dass es sich bei diesen Differentialen um keine vollständigen handelt.
Zweiter Hauptsatz
Es gibt einige Energieumwandlungen die nach dem Ersten Haupsatz der Thermodynamik
zwar erlaubt, aber in der Realität nie beobachtet werden. Der Zweite Hauptsatz schränkt
nun die erlaubten Energieumwandlungen weiter ein. Streng begründet werden kann er erst
im Rahmen der Statistischen Physik. Eine Formulierung des Zweiten Haupsatzes ist die
Clausiussche Aussage:
Es gibt keine periodisch arbeitende Maschine, die lediglich einem kälteren Wärmebad Wärme
entzieht und diese einem heißeren Wärmebad zuführt.
Die mathematische Formulierung des Zweiten Haupsatzes lautet:
dS ≥
δQ
T
(2.7)
Das Gleichheitszeichen in Gl.(2.7) wird für reversible Prozesse angenommen. Aus Gleichung
Gl.(2.7) folgt auch:
δQrev ≥ δQ
(2.8)
Bei irreversiblen Prozessen wird also verwertbare Energie verschenkt.
2.1.5 Kreisprozess
Bei einem Kreisprozess durchläuft ein thermodynamisches System verschiedene Austauschkontakte und kehrt schließlich in seinen Ausgangszustand zurück. Die Umgebung kann sich
dabei durchaus geändert haben.
9
2 Theoretische Grundlagen
Wärmekraftmaschine
Eine Wärmekraftmaschine ist ein thermodynamisches System, das einen Kreisprozess
zwischen zwei Wärmebädern durchläuft, ein Wärmebad bei der Temperatur Th und ein
Wärmebad bei der Temperatur Tc , dabei gilt Th > Tc . Die Maschine nimmt Wärme
∆Q1 > 0 vom wärmeren Wärmebad auf, leistet damit Arbeit ∆W < 0 und gibt Wärme
∆Q2 < 0 an das kältere Wärmebad ab. Damit der Erste Hauptsatz erfüllt wird, muss gelten:
|∆Q2 | < |∆Q1 |. Für eine Wärmekraftmaschine kann man einen sogenannten Wirkunsgrad
definieren, der angibt wie effizient eine Maschine läuft. Der Wirkungsgrad ist definiert als:
η=
−∆W
∆Q1
(2.9)
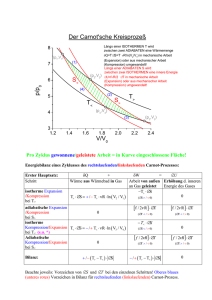
Carnot-Kreisprozess
Der Carnot-Kreisprozess ist ein spezieller reversibler Kreisprozess der aus zwei adiabatischen
und zwei isothermen Zustandsänderungen besteht. Die adiabatische Zustandsänderung ist
charakterisiert durch keinen Wärmeaustausch und die isotherme Zustandsänderung läuft
bei konstanter Temperatur ab. Der Wirkungsgrad der Carnot-Maschine beträgt
ηC = 1 −
Th
Tc
(2.10)
Der Carnot-Wirkungsgrad ist der höchste Wirkungsgrad der von einer reversibel arbeitenden
Maschine, die periodisch zwischen zwei Wärmebädern arbeitet, erreicht werden kann.
2.1.6 Endoreversible Thermodynamik
Die endoreversible Thermodynamik[2] ist ein Konzept um irreversible Prozesse beschreiben
zu können. Man unterteilt das thermodynamische System in intern reversible Subsysteme.
Zwischen den Subsystemen können irreversible Interaktionen stattfinden. Eine wichtige
Anwendung der endoreversiblen Thermodynamik ist die Curzon-Ahlborn-Maschine. Sie
besteht aus zwei Wärmebädern bei den konstanten Temperaturen Th und Tc und einer
reversibel arbeitenden Carnot-Maschine zwischen den Temperaturen Tih und Tic . Es gilt
dabei Th > Tih > Tic > Tc . Die thermischen Verbindungen zwischen den beiden Wärmebädern und der Carnot-Maschine sind irreversibel, man modelliert die Verluste über das
Newtonsche Wärmeleitungsgesetz. Den Wirkungsgrad der Maschine bei maximaler Leistung
bezeichnet man als Curzon-Ahlborn-Wirkungsgrad. Er beträgt
r
ηCA = 1 −
Tc
Th
(2.11)
In [1] konnte gezeigt werden, dass der Curzon-Ahlborn-Wirkungsgrad eine obere Schranke
in der linearen irreversiblen Thermodynamik darstellt.
10
2.2 Brownsche Bewegung
2.2 Brownsche Bewegung
Bewegt sich ein schweres Teilchen der Masse m und der Geschwindigkeit v in einer Flüssigkeit
von leichten Teilchen, so spricht man von einer “brownschen Bewegung”[8] des schweren
Teilchens. Das schwere Teilchen wird von den Molekülen der Flüssigkeit in unregelmäßiger
Weiße gestoßen. Diese Stöße bewirken eine mittlere bremsende Kraft und eine um diesen
Mittelwert fluktuierende stochastische Kraft f (t).
2.2.1 Langevin-Gleichung
Für die Bewegung des Teilchens können wir nun eine Bewegungsgleichung aufstellen. Die
mittlere bremsende Kraft auf das Teilchen wird durch den Term −mζv modelliert, wobei
ζ Reibungskoeffizient genannt wird. Die Bewegungsgleichung für das Problem nennt man
Langevin-Gleichung:
mv̇ = −mζv + f (t)
(2.12)
Dabei ist m die Masse und v die Geschwindigkeit des Teilchens. An die stochastische Kraft
f (t) muss man nun gewisse Annahmen machen, um Aussagen über die Lösung von Gl.(2.12)
machen zu können. Wir nehmen für unsere Brownsche Bewegung an, dass der zeitliche
Mittelwert der stochastischen Kraft verschwindet, da die stoßenden Moleküle der Flüssigkeit
aus allen Richtungen auf das schwere Teilchen wirken.
hf (t)i = 0
(2.13)
Die Autokorrelationsfunktion ist ein Maß, inwieweit eine Funktion von ihrer Vorgeschichte
abhängt. Wir modellieren sie hier mit einer Delta-Funktion, da wir uns für den Zeitverlauf
des schweren Teilchens auf einer weit größeren Skala interessieren als die Korrelationszeit
der stochastischen Kraft.
(2.14)
hf (t) f (t0 )i = λδ (t − t0 )
Der Koeffizient λ ist ein Maß für die Stärke des Schwankungsquadrats der stochastischen
Kraft. Determinierte Lösungen der Gl.(2.12) können nur für die Momente und Kumulanten
der Geschwindigkeit v (t) angegeben werden, da die stochastische Kraft f (t) auch nur
determinierte Aussagen über ihren Mittelwert und der Autokorrelationsfunktion enthält.
Der Reibungskoeffizient ζ und der Koeffizient λ sind über die Einstein-Beziehung miteinander
verknüpft:
λ = 2ζmkB T
(2.15)
Dabei ist kB die Boltzmann-Konstante und T die Temperatur.
2.2.2 Langevin-Gleichung in einem Kraftfeld
Befindet sich das zu beschreibende Teilchen zusätzlich in einem äußeren Kraftfeld K (x),
mit
∂V (x)
K (x) = −
(2.16)
∂x
11
2 Theoretische Grundlagen
wobei V (x) das zum Kraft gehörige Potential ist, dann lautet die Langevin-Gleichung:
mẍ = −mζ ẋ + K (x) + f (t)
(2.17)
Ein wichtiger Speziallfall von Gl.(2.17) ist der Grenzfall starker Dämpfung. Hier ist die
mittlere Bremsende Kraft verursacht durch die Stöße mit den Molekülen sehr viel größer
als die resultierende Kraft auf das schwere Teilchen. Es gilt also mζ ẋ >> mẍ. Die Gl.(2.17)
vereinfacht sich dadurch zu:
mζ ẋ = K (x) + f (t)
(2.18)
Wir betrachten Gl.(2.18) zunächst ohne die stochastische Kraft f (t). Die zeitliche Änderung
des Orts verschwindet genau dann, wenn die Kraft verschwindet. Das Teilchen wird also in
ein Minimum des Potentials streben und dort bleiben. Durch die stochastische Kraft bleibt
das Teilchen selbst im Potentialminimum nicht in Ruhe, sondern wird dort fluktuieren. Wenn
die Amplituden der stochastischen Kraft größer als die lokalen Potentialdifferenzen zwischen
Potentialminimas und -maximas sind, kann das Teilchen von einem lokalen Minimum in
ein anderes gelangen. Würde man die Amplitude der stochastischen Kraft langsam genug
zeitlich verkleinern, so ist Gl.(2.18) geeignet um für komplizierte Potentialverläufe das
globale Minimum zu finden.
2.2.3 Fokker-Planck-Gleichung
Die Langevin-Gleichungen sind stochastische Differentialgleichungen und somit gibt es keine
determinierte Lösung der Gleichungen. Aus den Langevin-Gleichungen lassen sich die sogenannten Fokker-Planck-Gleichungen herleiten, die die Warscheinlichkeitsdichte als Lösung
liefern. Durch die stochastische Kraft und ihren Eigenschaften kann man für Geschwindigkeit
und Ort des Teilchens zu einer bestimmten Zeit nur noch Wahrscheinlichkeiten angeben.
Die Fokker-Planck-Gleichung ist im Gegensatz zur Langevin-Gleichung keine stochastische
Differentialgleichung. Meistens benutzt man zur Herleitung der Fokker-Planck-Gleichung
für eine bestimmte Langevin-Gleichung die Eigenschaften in Gl.(2.13) und Gl.(2.14) für
die stochastische Kraft. Weiterhin nimmt man an, dass die stochastische Kraft einer GaußVerteilung genügt. Die Fokker-Planck-Gleichung zur Langevin-Gleichung in Gl.(2.12) lautet:
∂
∂
kB T ∂ 2
p (v, t)
p (v, t) = ζ
[vp (v, t)] + ζ
∂t
∂v
m ∂v 2
(2.19)
Die Wahrscheinlichkeitsdichte p (v, t) gibt nun an, mit welcher Wahrscheinlichkeit das Teilchen zur Zeit t die Geschwindigkeit [v, v + dv] besitzt. Die Fokker-Planck-Gleichung für die
Langevin-Gleichung in Gl.(2.18) nennt man Smoluchowski-Gleichung. Sie ist Ausgangspunkt
für das in dieser Arbeit vorgestellte Modell einer stochastische Wärmekraftmaschine und
lautet:
∂
∂
∂2
p (x, t) = −µ [p (x, t) K (x)] + µkB T 2 p (x, t)
(2.20)
∂t
∂x
∂x
12
2.2 Brownsche Bewegung
Dabei ist µ := (mζ)−1 die Beweglichkeit des Teilchens. Gl.(2.20) kann auch in der Form
einer Kontinuitätsgleichung geschrieben werden:
∂
∂
p (x, t) = − j (x, t)
∂t
∂x
∂
mit der Wahrscheinlichkeitsstromdichte j (x, t) := µ K (x) − kB T
p (x, t).
∂x
(2.21)
13
2 Theoretische Grundlagen
14
3 Durchführung
Im Gegensatz zu makroskopischen Systemen spielen bei mikroskopischen Systemen thermische Fluktuationen eine Rolle. Die Auswirkung davon ist, dass die Bahn eines Teilchen nicht
mehr determiniert ist. Anstelle der Newtonschen Bewegungsgleichung tritt die LangevinGleichung aus Kap. 2.2.1 bzw. Kap. 2.2.2. Man kann nur noch mit einer gewissen Wahrscheinlichkeit den Ort des Teilchens zu einer bestimmten Zeit angeben. Die zu dem Teilchen
gehörige Wahrscheinlichkeitsdichte wird durch eine Fokker-Planck Gleichung beschrieben.
In [9] konnte gezeigt werden, dass für die Bahn eines einzelnen Teilchens eine „stochastische
Entropie“ definiert werden kann, die dann ein konsistentes Bild für die Entropieproduktion
entlang einer einzelnen zufälligen Trajektorie eines Teilchens liefert. Damit können wir eine
thermodynamische Beschreibung für mikroskopische Teilchen verwenden. In dieser Arbeit
wollen wir einen Kreisprozess für kolloidartige Teilchen konstruieren, bestehend aus zwei
isothermischen und zwei adiabatischen Zustandsänderungen. Dabei wollen wir zunächst
wichtige thermodynamische Größen mit Hilfe der Fokker-Planck-Gleichung definieren. Anschließend analysieren wir die isothermen und die adiabatischen Zustandsänderungen und
geben danach die Konstruktion des Kreisprozesses an. Weiterhin wollen wir das System am
Punkt maximaler Leistung betrachten. Als Beispiel betrachten wir am Ende ein Kolloid in
einem harmonischen Potential.
3.1 Modell einer stochastische Wärmekraftmaschine
Die Wahrscheinlichkeitsdichte p (~x, τ ) eines mikroskopisches Teilchen in einem zeitabhängigen Potential V (~x, τ ) bei der Temperatur T lässt sich im überdämpften Fall durch die in
Kapitel 2.2.3 beschriebene Smoluchoswki-Gleichung (2.20) beschreiben. Wir geben sie hier
im 3 dimensionalen Fall an:
∂
p (~x, τ ) = −∇µ [− (∇V (~x, τ )) − kB T ∇] p (~x, τ ) = −∇~j (~x, τ )
∂τ
(3.1)
Dabei ist µ die Beweglichkeitsmatrix und kB die Boltzmann-Konstante. Die Wahrscheinlichkeitsdichte p (~x, τ ) gibt an, mit welcher Wahrscheinlichkeit das Teilchen sich am Ort ~x
zur Zeit τ befindet. Für ein einzelnes Teilchen führen wir nun wie in [9] die zeitabhängige
“System-Entropie” s (τ ) wie folgt ein:
s (τ ) = −kB ln p (~x, τ )
(3.2)
Diese Entropie ist abhängig von p (~x, τ ) und somit von der Startverteilung p (~x, 0), die
wiederum Informationen über das gesamte Ensemble beinhaltet. Die mittlere Entropie
15
3 Durchführung
S (τ ) = hs (τ )i wird dann zu:
Z
S (τ ) = −kB
p (~x, τ ) ln p (~x, τ ) dV
(3.3)
Wir können nun noch weiter eine mittlere innere Energie einführen:
Z
E (τ ) =
p (~x, τ ) V (~x, τ ) dV
(3.4)
Diese Definition ist nur korrekt für den Fall der überdämpften Langevin-, bzw. FokkerPlanck-Gleichung, die wir hier gewählt haben. Im nicht überdämpften Fall müsste die
kinetische Energie des Teilchens mit berücksichtigt werden.
3.1.1 Isotherme Zustandsänderungen
Für die isothermen Zustandsänderungen halten wir die Temperatur T in Gl.(3.1) fest. Die
isotherme Zustandsänderung findet in der Zeit ti ≤ τ ≤ tf statt. In dieser Zeit soll sich das
Potential V (~x, τ ) ändern. Mit Hilfe der gemittelten System-Entropie in Gl.(3.3) und der
mittleren inneren Energie in Gl.(3.4) können wir eine Kombination aus Ersten und Zweiten
Haupsatz aufschreiben:
∆E = T ∆S + W − Wirr
(3.5)
∆E ist die Energie- und ∆S die Entropieänderung. Weiterhin ist W die verrichtete bzw.
geleistete Arbeit und Wirr ist die irreversible Arbeit, die bei der Zustandsänderung als
nutzbare Arbeit verloren geht. Nach Gl.(2.7) kann man den Term T ∆S als reversible Wärme
∆Qrev auffassen. Da aber auch die Gl.(2.8) gilt können wir T ∆S − Wirr als irreversible
Wärme ∆Q interpretieren. Für die Arbeit und die irreversible Arbeit wollen wir nun die
entsprechenden Ausdrücke herleiten. Dazu müssen wir uns zunächst die Energie- und
Entropieänderung anschauen:
Zte ∆E =
∂E
∂τ
dτ
Gl.(3.4)
=
ti
(3.6)
ti
Zte ∆S =
ti
16
Zte Z h
i
ṗ (~x, τ ) V (~x, τ ) + p (~x, τ ) V̇ (~x, τ ) dV dτ
∂S
∂τ
dτ
Gl.(3.3)
=
Zte Z
−kB
ti
ṗ (~x, τ ) [ln p (~x, τ ) + 1] dV dτ
(3.7)
3.1 Modell einer stochastische Wärmekraftmaschine
Wir stellen Gl.(3.5) nach W um und setzen jeweils die rechte Seite von Gl.(3.6) und Gl.(3.7)
ein.
W = Wirr − T ∆S + ∆E
Zte Z h
i
= Wirr +
ṗ (~x, τ ) V (~x, τ ) + p (~x, τ ) V̇ (~x, τ ) dV dτ
(3.8)
ti
Zte Z
+ kB T
ṗ (~x, τ ) [ln p (~x, τ ) + 1] dV dτ
ti
Zte Z
= Wirr +
p (~x, τ ) V̇ (~x, τ ) dV dτ
ti
Zte Z
+
ṗ (~x, τ ) [V (~x, τ ) + kB T (ln p (~x, τ ) + 1)] dV dτ
(3.9)
ti
Wir formen den dritten Term in Gl.(3.9) um. Zunächst setzen wir Gl.(3.1) in der Form
ṗ (~x, τ ) = −∇~j ein. Danach führen wir partielle Integration aus:
Zte Z
ṗ (~x, τ ) [V (~x, τ ) + kB T (ln p (~x, τ ) + 1)] dV dτ =
ti
−
Zte Z ∇~j [V (~x, τ ) + kB T (ln p (~x, τ ) + 1)] dV dτ =
ti
Zte Z
−
∇ ~j [V (~x, τ ) + kB T (ln p (~x, τ ) + 1)] dV dτ
ti
|
{z
}
= 0, siehe [4]
Zte Z
+
~j [∇V (~x, τ ) + kB T ∇ (ln p (~x, τ ) + 1)] dV dτ =
ti
Zte Z
ti
)
Zte (Z ~ −1~
∇p
(~
x
,
τ
)
jµ
j
~j ∇V (~x, τ ) + kB T
dV dτ = −
dV dτ
p (~x, τ )
p (~x, τ )
ti
Im letzten Schritt haben wir benutzt, dass sich ∇V (~x, τ ) durch Gl.(3.1) folgendermaßen
umformen lässt:
µ−1~j
∇p (~x, τ )
∇V (~x, τ ) = −
− kB T
p (~x, τ )
p (~x, τ )
17
3 Durchführung
Damit lässt sich Gl.(3.8) schreiben als:
Zte Z
W = Wirr +
)
Zte (Z ~ −1~
jµ j
p (~x, τ ) V̇ (~x, τ ) dV dτ −
dV dτ
p (~x, τ )
ti
(3.10)
ti
Jetzt müssen wir noch bestimmen, welcher der beiden Terme für die Irreversibilität verantwortlich ist. Der rechte Term in Gl.(3.10) enthält die Wahrscheinlichkeitsstromdichte ~j.
Diese Wahrscheinlichkeitsstromdichte ist dafür verantwortlich, dass sich die Wahrscheinlichkeitsdichte p (~x, τ ) zeitlich ändert. Da die reversible Thermodynamik von zeitlich unveränderlichen Wahrscheinlichkeitsdichten ausgeht, können wir den rechten Term in Gl.(3.10)
mit der irreversiblen Arbeit identifizieren:
Wirr
)
Zte (Z ~ −1~
jµ j
=
dV dτ
p (~x, τ )
(3.11)
ti
Zte Z
W =
p (~x, τ ) V̇ (~x, τ ) dV dτ
(3.12)
ti
3.1.2 Adiabatische Zustandsänderungen
Die adiabatischen Zustandsänderungen laufen unendlich schnell ab und sind somit nur eine
idealisierte Beschreibung realer thermodynamischer Prozesse, die sehr schnell ablaufen und
kaum Wärme mit der Umgebung austauschen. In diesem Modell werden die adiabatischen
Zustandsänderungen durch Sprünge im Potential V (~x, τ ) realisiert. Da für die Zustandsänderung keine Zeit vergeht, kann sich weder die Wahrscheinlichkeitsdichte p (~x, τ ) noch die
mittlere System-Entropie zeitlich verändern. Durch den Sprung im Potential ändert sich
aber die innere Energie:
Z
∆E = p (~x, τ ∗ ) [V (~x, τ ∗ + 0) − V (~x, τ ∗ − 0)] dV
(3.13)
Auch für diese Zustandsänderung gilt Gl.(3.5), die sich hier vereinfacht zu:
∆E = W
(3.14)
3.1.3 Konstruktion des Prozesses
Der Kreisprozess soll nun aus zwei isothermen und zwei adiabatischen Zustandsänderungen
bestehen. Im folgenden wird beschrieben, wie die Schritte nacheinander ablaufen sollen:
1. Schritt:
isotherme Zustandsänderung bei der Temperatur T = Th in der Zeit 0 < τ < t1
18
3.1 Modell einer stochastische Wärmekraftmaschine
2. Schritt:
adiabatische Zustandsänderung zur Zeit τ = t1 . Dabei ändert sich die Temperatur
von Th auf Tc . Es gilt dabei Th > Tc . Die Wahrscheinlichkeitsdichte ändert sich nicht,
aber das Potential springt an dieser Stelle.
3. Schritt:
isotherme Zustandsänderung bei der Temperatur T = Tc in der Zeit t1 < τ < t1 + t3 .
4. Schritt:
adiabatische Zustandsänderung zur Zeit τ = t1 + t3 . Dabei ändert sich die Temperatur
von Tc auf Th . Auch hier ändert sich die Wahrscheinlichkeitsdichte wie im 2. Schritt
nicht, aber das Potential springt wieder.
Wir wollen nun bestimmen, wie sich die gesamte Arbeit W im Kreisprozess zusammensetzt.
Da es sich um einen Kreisprozess handelt, darf sich die Entropie und die Energie nach
jeweils vollständigen Durchläufen nicht geändert haben. Es gilt also:
∆E
ges
=
∆S ges =
4
X
∆E (i) = 0
(3.15)
∆S (i) = 0
(3.16)
i=1
4
X
i=1
Dabei gibt i den i. Schritt des Kreisprozesses an. Weiterhin wissen wir, dass sich bei den
adiabatischen Zustandsänderungen die Entropie nicht ändert, also ∆S (2) = ∆S (4) = 0.
Daraus folgt aber nach Gl.(3.16), dass ∆S (1) = −∆S (3) =: ∆S ist. Die gesamte Arbeit im
Kreisprozess ergibt sich nun nach Gl.(3.8):
W =
W =
4
X
W (i) =
i=1
(1)
Wirr
+
4
X
i=1
(3)
Wirr −
(i)
Wirr −
4
X
Ti ∆S (i) +
i=1
(Th − Tc ) ∆S =
4
X
∆E (i)
i=1
ges
Wirr
− ∆T ∆S
(3.17)
Aus Gl.(3.17) sehen wir, dass nur die isothermen Zustandsänderungen Anteil an der Gesamtarbeit W im Kreisprozess haben. Einfluss auf den Wert der Gesamtarbeit hat neben
(1)
(3)
ges
der gesamten irreversiblen Arbeit Wirr
:= Wirr + Wirr auch die Temperaturdifferenz
∆T := Th − Tc . Die Wärmeaufnahme vom Wärmebad bei der Temperatur Th während eines
gesamten Durchlaufes des Kreisprozess beträgt:
(1)
Q(1) = ∆E (1) − W (1) = Th ∆S − Wirr
(3.18)
19
3 Durchführung
3.1.4 Wirkungsgrad und maximale Leistung
Der Wirkungsgrad für diesen Prozess kann nach Gl.(2.9) in folgender Form geschrieben
werden:
η=
−W
ηC
=
=
(1)
Q(1)
∆T ∆S Wirr
−
ηC

−W
−W


ηC


(1)
Wirr
 

1
∆T
 

∆S
ges  − 
ges  ηC
Wirr
Wirr
1−
1−
∆T ∆S
∆T ∆S

(3.19)
Wir wollen nun einen Ausdruck für die maximale Leistung bestimmen und den Wirkunsgrad
am Punkt maximaler Leistung berechnen. Wir gehen zurück zu der in Gl.(3.1) angegebenen
Smolouchowski-Gleichung und wählen die Darstellung als Kontinuitätsgleichung ṗ (~x, τ ) =
−∇~j (~x, τ ). Der Term für die irreversible Arbeit in Gl.(3.11) enthält die Integration über
die Zeit und den Ort. Wenn wir für die Zeit die Transformation
τ̃ =
τ − ti
te − ti
(3.20)
wählen, dann gilt 0 ≤ τ̃ ≤ 1. Die Gl.(3.1) können wir nun auch umrechnen auf die neue
Zeitvariable τ̃ . Es gilt:
∂
∂ ∂ τ̃
1
∂
=
=
∂τ
∂ τ̃ ∂τ
te − ti ∂ τ̃
τ (τ̃ ) = (te − ti ) τ̃ + ti
Damit wird Gl.(3.1) zu:
1
∂
p (~x, τ (τ̃ )) = −∇~j (~x, τ (τ̃ ))
te − ti ∂ τ̃
(3.21)
Wenn wir nun
p̃ (~x, τ̃ ) := p (~x, τ (τ̃ ))
~˜j (~x, τ̃ ) := (te − ti ) ~j (~x, τ (τ̃ ))
(3.22)
(3.23)
als transformierte Wahrscheinlichkeitsdichte und transformierte Wahrscheinlichkeitsstromdichte definieren, dann lässt sich Gl.(3.1) schreiben als:
∂
˜
p̃ (~x, τ̃ ) = −∇~j (~x, τ̃ )
∂ τ̃
(3.24)
Die Gl.(3.24) hat nun die gleiche Form wie Gl.(3.1) und deshalb kann der Ausdruck für die
irreversible Arbeit in Gl.(3.11) auch umgerechnet werden auf die transformierten Größen.
20
3.1 Modell einer stochastische Wärmekraftmaschine
Aus dτ = (te − ti ) dτ̃ und Gl.(3.22), Gl.(3.23) folgt nun für die irreversible Arbeit:
Wirr


1 ~˜
1 ~˜
)
Zte (Z ~ −1~
Z1 
Z
j (~x, τ̃ ) µ−1
j (~x, τ̃ ) 


jµ j
te − ti
te − ti
=
dV dτ = (te − ti )
dV dτ̃


p (~x, τ )
p̃ (~x, τ̃ )


ti
0
Wirr
1
=
te − ti
)
Z1 (Z ~˜
˜
Airr
j (~x, τ̃ ) µ−1~j (~x, τ̃ )
dV dτ̃ =
p̃ (~x, τ̃ )
te − ti
0
(3.25)
Durch die Transformation kann der Ausdruck für die irreversible Arbeit in die zeitunabhängige Wirkung Airr , die linear mit der Zeitspanne te − ti der isothermen Zustandsänderung
skaliert, überführt werden. Für beide isothermen Zustandsänderungen in unserem Kreisprozess ergibt sich also:
(i)
(i)
Wirr =
Airr
, i = 1, 3
ti
(3.26)
und damit die gesamte Arbeit nach Gl.(3.17) zu:
(1)
(3)
A
A
W = irr + irr − ∆T ∆S
t1
t3
(3.27)
Die Leistung ist definiert als:
(1)
(3)
A
A
∆T ∆S − irr − irr
−W
t1
t3
P =
=
t1 + t3
t1 + t3
(3.28)
Wir wollen zunächst überprüfen, ob es Zeiten t∗1 , t∗3 gibt, für die die Leistung maximal wird.
Dazu berechnen wir die ersten und zweiten partiellen Ableitungen der Leistung nach den
Zeiten t1 , t3 . Nachfolgend ist i, j ∈ {1, 3} ; i 6= j.
∂W
∂P
W
−1
∂W
∂ti
=
+
=
+P
∂ti
t1 + t3 (t1 + t3 )2
t1 + t3 ∂ti
2
2
1
∂P
∂P
∂ 2P
∂W
1
∂ W
−1
∂ W
=
+P −
+
=
+2
∂t2i
t1 + t3 ∂t2i
∂ti
t1 + t3 ∂t2i
∂ti
(t1 + t3 )2 ∂ti


2

∂ 2P
1
∂W
1 
∂
W
∂P
−1
∂P
∂P

=
=
+P −
+
+
∂tj ∂ti
t1 + t3  ∂tj ∂ti ∂tj  t1 + t3 ∂ti
∂tj
(t1 + t3 )2 ∂ti
| {z }
−
=0
21
3 Durchführung
∂P ∂P Für
=
= 0 wird
∂t1 t∗
∂t3 t∗
1
3
∂ 2 W ∂t2i t∗ ,t∗
∂ 2 P = − ∗ 1∗
∂t2i t∗ ,t∗
t1 + t3
1
3
(i)
=−
3
und
2Airr
≤0
∗3 ∗
ti (t1 + t∗3 )
∂ 2 P =0
∂ti ∂tj t∗ ,t∗
1
3
Damit wird die Hesse-Matrix H an der Stelle t∗1 , t∗3
 2 
∂ P ∂ 2 P  ∂t2 ∗ ∗ ∂t ∂t ∗ ∗ 
1 3 t ,t 

1
1 3  = −2
H t∗ ,t∗ =  2 t1 ,t3
2 ∂
P
∂
P
1 3

 t∗1 + t∗3
2 ∂t3 ∂t1 t∗ ,t∗
∂t3 t∗ ,t∗
1
3
1

(1)
A
 ∗irr3
 t1


0
3

0 

(3) 
Airr 
t∗3 3
negativ definit und somit wird die Leistung an der Stelle t∗1 , t∗3 maximal, wenn dort auch die
ersten partiellen Ableitungen verschwinden. Als nächstes berechnen wir die Werte für t∗1 , t∗3 .
∂P !
=0
∂ti ∗
ti
(1)
A
I : − ∗irr2 + P = 0
t1
(3)
II : −
III = I − II : −
(i)
A
+
− ∗irr
ti 2
Airr
+P =0
t∗3 2
(1)
Airr
t∗1 2
+
(3)
Airr
t∗3 2
(i)
(j)
(i)
(j)
v
u (1)
t∗1 u
A
= 0 ⇒ ∗ = t irr
(3)
t3
Airr
Airr
A
− irr
∗
ti
t∗j
= 0 · (t∗1 + t∗3 )
∗
∗
t1 + t3
∆T ∆S −
(i)
⇒ (t∗1 + t∗3 )
Airr Airr Airr
+ ∗ + ∗ = ∆T ∆S
ti
tj
t∗i 2
(i)
(i)
(j)
Airr t∗j Airr Airr
⇒ 2 ∗ + ∗ ∗ + ∗ = ∆T ∆S
ti
ti ti
tj
q
(i) (j)
(i)
Airr Airr
III Airr
⇒2 ∗ +2
= ∆T ∆S
ti
t∗i
q
q
(i) 2
2Airr
(i)
(i) (j)
(j)
(i)
∗
⇒ ti =
Airr + Airr Airr =
1 + Airr /Airr
∆T ∆S
∆T ∆S
22
(3.29)
3.1 Modell einer stochastische Wärmekraftmaschine
(i) ∗
Die irreversible Arbeit der einzelnen isothermen Zustandsänderungen Wirr und die gesamte
ges ∗
irreversible Arbeit im Kreisprozess Wirr
beträgt bei maximaler Leistung:
(i) ∗
Wirr =
(i)
Airr
t∗i
1
∆T ∆S
2q
=
1+
(j)
(i)
Airr /Airr
1
ges ∗
Wirr
= ∆T ∆S
2
(3.30)
(3.31)
Somit wird die Arbeit W ∗ im Kreisprozess nach Gl.(3.17) zu:
1
W ∗ = − ∆T ∆S
2
(3.32)
und die Gesamtzeit für einen Durchlauf des Kreisprozess beträgt:
t∗1
+
t∗3
2
=
∆T ∆S
q
2
q
(1)
(3)
Airr + Airr
(3.33)
Damit wird die maximale Leistung nach Gl.(3.28):
2
1
∆T ∆S


q
P ∗ = q 2

(1)
(3)
Airr + Airr

(3.34)
und der Wirkungsgrad bei maximaler Leistung wird nach Gl.(3.19) zu:
η∗ =
mit:
ηC
2 − γηC

(3.35)

1
γ=
1+
q
(3)
(1)
Airr /Airr

(3.36)
Der Wirkungsgrad bei maximaler Leistung enthält den Koeffizienten γ, der das Verhältnis
(i)
der irreversiblen Wirkungen Airr beinhaltet. Wenn die Mobilitätsmatrix µ isotrop ist, dann
(3)
(1)
ist sie nur noch von der Temperatur abhängig und es gilt Airr /Airr = µ (Th ) /µ (Tc ). Wenn
die Mobilitätsmatrix auch nicht von der Temperatur abhängig ist, dann gilt γ = 12 . In der
Gl.(3.34) für die maximale Leistung treten die irreversiblen Wirkungen nicht im Verhältnis
auf und man benötigt das explizite Potential V (~x, τ ) um diese zu berechnen. Wenn man
sich für das Potential nur die Ortsverteilung vorgibt, kann man über optimale Steuerung
bzw. Variationsmethoden die zeitliche Steuerung des Potentials berechnen, für die die
irreversiblen Wirkungen minimal werden.
23
3 Durchführung
3.2 Ein Kolloid in einem harmonischem Potential
Wir untersuchen nun eine spezielle stochastische Wärmekraftmaschine im eindimensionalen
Ortsraum. Es handelt sich dabei um ein Kolloid in einem harmonischem Potential, dessen
Stärke jedoch zeitlich veränderlich ist. Das Potential wollen wir schreiben als:
V (x, τ ) = λ (τ ) x2 /2
(3.37)
wobei λ (τ ) eine beliebige zeitabhängige Funktion ist. Auf das Kolloid wirkt zusätzlich eine
stochastische Kraft, deren zeitlicher Mittelwert Null und die zusätzlich delta-korreliert ist.
Die Bewegung des Teilchen wird nun im überdämpften Fall durch die Langevin-Gleichung
in Gl.(2.18) beschrieben. Die zugehörige Fokker-Planck-Gleichung ist die Smoluchowski∂
Gleichung in Gl.(2.20). In diesem Fall lautet die Kraft K (x, τ ) = − V (x, τ ) = −λ (τ ) x
∂x
und die Smoluchowski-Gleichung lässt sich schreiben als:
∂
∂
∂2
p (x, τ ) = µλ (τ )
[xp (x, τ )] + µkB T 2 p (x, τ )
∂τ
∂x
∂x
(3.38)
3.2.1 Herleitung der Differentialgleichung für die Varianz des
Teilchenorts
Kennt man die Lösung von Gl.(3.38), so weiß man mit welcher Wahrscheinlichkeit sich
das Kolloid im Intervall [x, x + dx] zur Zeit τ befindet. Da sich unser Kolloid in einem
harmonischen Potential befindet, ist die Varianz
w (τ ) = hx2 (τ )i − hx (τ )i2 =
Z∞

x2 p (x, τ ) dx − 
−∞
2
Z∞
xp (x, τ ) dx
(3.39)
−∞
eine wichtige Größe, wie wir im folgenden noch sehen werden. Deshalb leiten wir aus Gl.(3.38)
eine Bewegungsgleichung für die Varianz her. Dafür benötigen wir den Ortsmittelwert
hx (τ )i des Kolloids und das zweite Moment hx2 (τ )i. Um eine Bewegungsgleichung für den
Ortsmittelwert hx (τ )i zu erhalten, betrachten wir die Gl.(3.38) zu einer festen Zeit und
multiplizieren sie mit x. Danach integrieren wir über den gesamten Ortsraum.
Z∞
∂
x p (x, τ ) dx = µλ (τ )
∂τ
−∞
Z∞
∂
x [xp (x, τ )] dx + µkB T
∂x
−∞
Z∞
x
∂2
p (x, τ ) dx
∂x2
−∞
Die linke Seite in Gl.(3.40) wird zu:
Z∞
−∞
24
∂
x p (x, τ ) dx =
∂τ
Z∞
−∞
∂
∂
[xp (x, τ )] dx =
hx (τ )i
∂τ
∂τ
(3.40)
3.2 Ein Kolloid in einem harmonischem Potential
und ist somit die zeitliche Ableitung des Ortsmittelwertes hx (τ )i des Kolloids. Der erste
Term auf der rechten Seiten in Gl.(3.40) lässt sich wie folgt auswerten:
Z∞
µλ (τ )
∂
x [xp (x, τ )] dx = µλ (τ )
∂x
Z∞
∂
p (x, τ ) dx
∂x
−∞
n
o
∞
2
= µλ (τ ) hx (τ )i + µλ (τ ) x p (x, τ ) −∞ −2hx (τ )i
|
{z
}
−∞
xp (x, τ ) + x2
=0
= −µλ (τ ) hx (τ )i
Der zweite Term in Gl.(3.40) verschwindet:
Z∞
µkB T
−∞
n ∂
∞
∂2
x 2 p (x, τ ) dx = µkB T x p (x, τ )−∞ −
∂x
| ∂x {z
}
=0
Z∞
o
∂
p (x, τ ) dx
∂x
−∞
|
{z
}
∞
=p(x,τ )
=0
−∞
=0
Somit liefert uns Gl.(3.40) folgende Bewegungsgleichung für den Ortsmittelwert des Kolloids:
∂
hx (τ )i = −µλ (τ ) hx (τ )i
∂τ
Diese Gleichung wird gelöst durch:
hx (τ )i = hx (0)ie
−µ
Rτ
(3.41)
λ(t)dt
(3.42)
0
Wenn wir also für unser Potential eine explizite Zeitabhängigkeit λ (τ ) einsetzen, dann
können wir eine Formel für den Ortsmittelwert unseres Kolloids angeben.
Wir müssen nun noch eine Bewegungsgleichung für das zweite Moment hx2 (τ )i herleiten.
Wir betrachten die Gl.(3.38) wieder zu einer festen Zeit und multiplizieren sie mit x2 .
Danach integrieren wir über den gesamten Ortsraum.
Z∞
∂
x
p (x, τ ) dx = µλ (τ )
∂τ
2
−∞
Z∞
∂
x
[xp (x, τ )] dx + µkB T
∂x
2
−∞
Z∞
x2
∂2
p (x, τ ) dx
∂x2
(3.43)
−∞
Auf der linken Seite von Gl.(3.43) ergibt sich:
Z∞
−∞
∂
x
p (x, τ ) dx =
∂τ
2
Z∞
∂ 2
∂ 2
x p (x, τ ) dx =
hx (τ )i
∂τ
∂τ
(3.44)
−∞
25
3 Durchführung
Der erste Term auf der rechten Seite von Gl.(3.43) lässt sich wie folgt auswerten:
Z∞
Z∞
∂
∂
µλ (τ )
x2
[xp (x, τ )] dx = µλ (τ )
x2 p (x, τ ) + x3 p (x, τ ) dx
∂x
∂x
−∞
−∞
n
o
∞
= µλ (τ ) hx2 (τ )i + µλ (τ ) x3 p (x, τ )−∞ −3hx2 (τ )i
|
{z
}
=0
2
= −2µλ (τ ) hx (τ )i
Der zweite Term auf der rechten Seite von Gl.(3.43) vereinfacht sich zu:
Z∞
Z∞
o
n ∂
2
∞
∂
2
2 ∂
p
(x,
τ
)
p
(x,
τ
)
dx
p
(x,
τ
)
dx
=
µk
T
x
µkB T
x
−2
x
B
−∞
∂x2
∂x
| ∂x {z
}
−∞
−∞
=0
= −2µkB T
n
xp (x, τ ) |∞
−∞
|
{z
=0
}
Z∞
−
p (x, τ ) dx
o
−∞
|
{z
=1
}
= 2µkB T
Wir erhalten somit für das zweite Moment folgende Bewegungsgleichung:
∂ 2
hx (τ )i = −2µλ (τ ) hx2 (τ )i + 2µkB T
(3.45)
∂τ
Wir können nun mit Gl.(3.41) und Gl.(3.45) eine Bewegungsgleichung für die Varianz
aufstellen:
∂ 2
∂
∂
w (τ ) =
hx (τ )i −
hx (τ )i2
∂τ
∂τ
∂τ
∂ 2
∂
=
hx (τ )i − 2hx (τ )i hx (τ )i
∂τ
∂τ
2
= −2µλ (τ ) hx (τ )i + 2µkB T + 2µλ (τ ) hx (τ )i2
= −2µλ (τ ) hx2 (τ )i − hx (τ )i2 + 2µkB T
∂
w (τ ) = −2µλ (τ ) w (τ ) + 2µkB T
(3.46)
∂τ
Die Differentialgleichung für das zweite Moment und die Differentialgleichung für die Varianz
sind identisch. Die Funktionen für das zweite Moment und für die Varianz fallen aber nur
dann zusammen, wenn der Ortsmittelwert zur Zeit Null hx (0)i = 0 ist. Denn dann ist der
Ortsmittelwert nach Gl.(3.42) für alle Zeiten Null.
Im folgenden nehmen wir nun an, dass hx (0)i = 0 gilt, damit wir w (τ ) = hx2 (τ )i benutzen
können. Die mittlere Energie im System lässt sich nach Gl.(3.4) nun schreiben als:
Z∞
Z∞
1
1
E (τ ) =
p (x, τ ) V (x, τ ) dx = λ (τ )
p (x, τ ) x2 dx = λ (τ ) w (τ )
(3.47)
2
2
−∞
26
−∞
3.2 Ein Kolloid in einem harmonischem Potential
Die mittlere Arbeit bei isothermer Zustandsänderung wird somit nach Gl.(3.12) zu:


Ztf  Z∞
Ztf

1
W =
p (x, τ ) V̇ (x, τ ) dx dτ =
w (τ ) λ̇ (τ ) dτ
(3.48)


2
ti
−∞
ti
Somit ist die mittlere Arbeit abhängig von der Funktion λ (τ ). Wir haben dadurch die
Möglichkeit, die mittlere Arbeit dieses Kreisprozesses zu maximieren, indem wir die optimale
Funktion λ (τ ) finden. Wir wollen nun einen Kreisprozess konstruieren, wie er in Kapitel
3.1.3 beschrieben wird. Die erste Isotherme soll sich bei der Temperatur Th befinden und
die zugehörige Zeitfunktion des Potential bezeichnen wir mit λ1 (τ ). Die zweite Isotherme
soll sich bei der Temperatur Tc befinden und die Zeitfunktion des Potential bezeichnen
wir hier mit λ3 (τ ). Die beiden Adiabaten, die die zwei Isothermen miteinander verbinden,
laufen unendlich schnell ab, so dass sich hier die Varianz w (τ ) nicht ändern kann und somit
auch das Potential V (x, τ ) konstant bleibt. Wir suchen nun die Funktionen λ1 (τ ) und
λ3 (τ ) für welche die Arbeit W bei den isothermen Zustandsänderungen maximal wird. Wir
formen zunächst Gl.(3.48) um, damit wir Ausdrücke für die irreversible Arbeit Wirr , die
Energieänderung ∆E und die Wärme Q erhalten.
1
W =
2
Ztf
1
w (τ ) λ̇ (τ ) dτ =
2
Ztf
ti
Gl.(3.46)
=
∂
1
[w (τ ) λ (τ )] dτ −
∂τ
2
ti
tf 1
1
w (τ ) λ (τ ) −
2
2
ti
Ztf
Ztf
λ (τ ) ẇ (τ ) dτ
ti
T
1 ẇ (τ )
−
ẇ (τ ) dτ
w (τ ) 2µ w (τ )
ti
tf 1
1
= w (τ ) λ (τ ) − T
2
2
ti
Ztf
ẇ (τ )
1
dτ +
w (τ )
4µ
ti
Ztf
ẇ2 (τ )
dτ
w (τ )
ti
t
Zf 2
tf 1
tf
1
1
ẇ (τ )
W = w (τ ) λ (τ ) − T ln [w (τ )] +
dτ
2
2
4µ
w (τ )
ti
ti
(3.49)
ti
Wir können nun die drei Terme identifizieren:
tf
1
∆E = w (τ ) λ (τ )
2
ti
tf
1
T ∆S = T ln [w (τ )]
2
ti
t
f
Z 2
1
ẇ (τ )
Wirr =
dτ
4µ
w (τ )
(3.50)
(3.51)
(3.52)
ti
Die Gl.(3.49) kann nun also in der Form wie in Gl.(3.8) geschrieben werden.
27
3 Durchführung
3.2.2 Maximierung der Arbeit des Kreisprozess
Wenn wir nun die Arbeit maximieren wollen, dann ist das äquivalent mit der Minimierung
der irreversiblen Arbeit in Gl.(3.52). Diese können wir schreiben als
Ztf
L (w (τ ) , ẇ (τ )) dτ
Wirr =
(3.53)
ti
ẇ2 (τ )
setzen. Die Euler-Lagrange-Gleichung liefert nun die
w (τ )
Bedingung[5], für welches w (τ ) die irreversible Arbeit extremal wird.
wenn wir L (w (τ ) , ẇ (τ )) =
d ∂L
∂L
−
=0
dt ∂ ẇ
∂w
1
ẇ2
d ẇ
− 2 −2
=0
4µ
w
dt w
ẇ2
ẅ
ẇ2
− 2 −2 +2 2 =0
w
w
w
2
ẇ − 2wẅ = 0
(3.54)
Löst man die Differentialgleichung in Gl.(3.54), erhält man die optimale Funktion für die
Varianz. Die Lösung dieser Gleichung lautet:
w (τ ) = c1 (c2 + τ )2
(3.55)
Dabei sind c1 , c2 Konstanten, die über die Randbedingungen festgelegt werden. Die isotherme
Zustandsänderung bei der Temperatur Th soll in der Zeit 0 ≤ τ ≤ t1 ablaufen und die
isotherme Zustandsänderung bei der Temperatur Tc in der Zeit t1 ≤ τ ≤ t1 + t3 . Es soll nun
gelten w (0) = w (t1 + t3 ) = wa und w (t1 ) = wb . Da es sich um einen Kreisprozess handelt,
muss die Varianz am Anfang und am Ende des Kreisprozesses gleich sein. Wir bestimmen
nun die Funktion w1 (τ ), die zur Isothermen bei T = Th gehört:
I : w1 (0) = wa = c1 c22
II : w1 (t1 ) = wb = c1 (c2 + t1 )2 = c1 c22 (1 + t1 /c2 )2 = wa (1 + t1 /c2 )2
r
r
II
wb
⇒
−1=
− 1 = t1 /c2
I
wa
r
wb
−1
wa
⇒
= 1/c2
t1
r
2
wb
τ
2
2
⇒ w1 (τ ) = c1 c2 (1 + τ /c2 ) = wa 1 +
−1
t1
wa
28
(3.56)
3.2 Ein Kolloid in einem harmonischem Potential
Nun benötigen wir noch die Funktion w3 (τ ), die zur Isothermen bei T = Tc gehört:
I : w3 (t1 ) = wb = c1 (c2 + t1 )2
II : w3 (t1 + t3 ) = wa = c1 (c2 + t1 + t3 )2
r
r
II
wa
c2 + t1 + t3
t3
=
=
=1+
I
wb
c2 + t1
c2 + t1
t3
⇒ c2 + t1 = r
wa
−1
wb
t3
− t1
⇒ c2 = r
wa
−1
wb
r
2
wa
wb
−1
wb
⇒ c1 =
t23
r
2 
2
wa
wb
−1


wb
 r t3

⇒ w3 (τ ) =
−
t
+
τ
1
 wa

t23
−1
wb
r
2
wa
τ − t1
⇒ w3 (τ ) = wb 1 +
−1
t3
wb
(3.57)
Die Zeitfunktionen λ1 (τ ) und λ3 (τ ) erhalten wir durch umstellen von Gl.(3.46) nach λ.
Wir führen für bessere Übersicht folgende Faktoren ein:
r
wb
−1
wa
wa
β=
µkB Th t1
α=
(3.58)
(3.59)
29
3 Durchführung
λ1 (τ ) =
=
λ3 (τ ) =
=
1
1
kB Th −
ẇ1
w1 (τ )
2µ
τ
1 − αβ 1 + α
kB Th
t1
2
wa
τ
1+ α
t1
1
1
kB Tc −
ẇ3
w3 (τ )
2µ
Tc t1
t1
τ
+ αβ α + 1 +
1−
α
kB Th Th t3
t3
t1
2
wa
t1
τ
α+1+
1−
α
t3
t1
(3.60)
(3.61)
Geben wir die Zeitfunktionen λ1 (τ ) und λ3 (τ ) in Einheiten von kB Th /wa an und die
Zeit τ in Einheiten von t1 , so ist λ1 (τ ) nur noch von den beiden Faktoren α und β
abhängig. Die Funktion λ3 (τ ) hängt zusätzlich zu diesen beiden Faktoren noch von dem
Temperaturverhältnis Tc /Th und dem Zeitverhältnis t1 /t3 ab. In Abb.3.1 ist der Verlauf
3.5
w1(τ)
w3(τ)
3
w/wa
2.5
2
1.5
1
0
0.5
1
τ/t1
1.5
2
Abbildung 3.1: Varianzfunktionen w1 (τ ) und w3 (τ ) bei folgenden Parametern:
α = 0.8, t1 /t3 = 1
der Varianzfunktionen und in Abb.3.2 der Verlauf der beiden Zeitfunktionen, zur Steuerung
30
3.2 Ein Kolloid in einem harmonischem Potential
1.8
λ1(τ)
λ3(τ)
1.6
λ/(kBTh/wa)
1.4
1.2
1
0.8
0.6
0.4
0
0.5
1
τ/t1
1.5
2
Abbildung 3.2: Varianzfunktionen λ1 (τ ) und λ3 (τ ) bei folgenden Parametern:
α = 0.8, β = 1, TThc = 21 , t1 /t3 = 1
des harmonischen Potentials dargestellt. In Abb.3.2 sehen wir auch deutlich den Sprung
der Steuerfunktion, genau bei der Adiabate. Da es sich um einen Kreisprozess handelt
und λ1 (0) 6= λ3 (t1 + t3 ) ist, haben wir an der Stelle τ = t1 + t3 noch einen Sprung in der
Steuerfunktion. Wir wollen den Betrag der Sprungstelle zur Zeit t1 mit ∆λt1 und zur Zeit
ttot := t1 + t3 mit ∆λttot bezeichnen. Es ergeben sich folgende Ausdrücke dieser beiden
Größen:
t1
Tc
kB Th 1 − Th + 1 − t3 αβ (1 + α)
∆λt1 =
wa
(1 + α)2
Tc
t1
kB Th ∆λttot =
1−
+ 1−
αβ wa
Th
t3
(3.62)
(3.63)
Je kleiner die Verhältnisse Tc /Th und t1 /t3 , desto größer sind die beiden Sprünge in der
Steuerfunktion.
31
3 Durchführung
Die minimale irreversible Arbeit können wir nun nach Gl.(3.52) berechnen:
(1)
Wirr
(3)
1
= 2 wa α 2
µt1
Wirr =
1
wa α 2
µt23
Zt1
dτ =
√ 2
1
1 √
wa α 2 =
( wa − wb )
µt1
µt1
0
tZ
1 +t3
dτ =
√ 2
1
1 √
wa α2 =
( wa − wb )
µt3
µt3
(3.64)
(3.65)
t1
(3.66)
Führen wir nun die irreversible Wirkung
Airr =
√ 2
1 √
( wb − wa )
µ
(3.67)
(i)
ein, so können wir die irreversible Arbeit schreiben als Wirr =
1
Airr . Die maximale Arbeit
ti
im Kreisprozess lässt sich nun nach Gl.(3.17) schreiben als:
1
1
+
W =
Airr − ∆T ∆S
(3.68)
t1 t3
1
wb
mit ∆T = Th − Tc und ∆S = ln
. Durch Einführung einer „reduzierten Zeit“
2
wa
tr =
1
t1
1
+
1
t3
=
t1 t3
t1 + t3
(3.69)
sieht man, dass die Arbeit W nur von dieser reduzierten Zeit abhängt. Wenn die reduzierte
Zeit den Wert
Airr
t0r =
(3.70)
∆T ∆S
annimmt, dann ist die Arbeit W im Kreisprozess Null. Für kleinere Werte der reduzierten
Zeit verbraucht die Maschine sogar Arbeit.
3.2.3 Berechnung des Wirkungsgrades
Für den Wirkungsgrad brauchen wir noch die Wärmeaufnahme Q(1) der Maschine vom
Wärmereservoir bei T = Th . Diese berechnet sich nach Gl.(3.18) zu:
(1)
Q(1) = Th ∆S − Wirr = Th ∆S −
Airr
t1
(3.71)
Der Wirkungsgrad unserer Maschine berechnet sich nach Gl.(2.9) nun zu:
∆T ∆S − Atirr
−W
r
η = (1) =
Q
Th ∆S − Atirr
1
32
(3.72)
3.2 Ein Kolloid in einem harmonischem Potential
Wenn wir die Zeiten der isothermen Zustandsänderung gegen Unendlich gehen lassen,
also t1 , t3 → ∞, dann verschwindet die irreversible Arbeit und wir erhalten den Carnot
Wirkungsgrad ηC = ∆T /Th = 1 − Tc /Th . Wir erkennen dadurch, dass jeder real ablaufende
thermodynamische Kreisprozess niemals den Carnot-Wirkungsgrad erreichen kann, da die
Zustandsänderungen immer in einer endlichen Zeit ablaufen.
3.2.4 Maximale Leistung
Die Leistung des Prozess ist definiert als
P =
−W
∆T ∆S
Airr
∆T ∆S Airr
=
−
=
−
t1 + t3
t1 + t3
tr (t1 + t3 )
t1 + t3
t1 t3
(3.73)
In jedem reversiblen Prozess wäre die Leistung Null, da die Zeiten der Zustandsänderungen
gegen unendlich gehen. Wir wollen nun die Werte von t1 , t3 bestimmen, für die wir die
maximale Leistung erhalten:
Airr
∂P
∆T ∆S
=−
=0
2 + 2
∂t1
t1 t3
(t1 + t3 )
Airr
∆T ∆S
∂P
=−
=0
2 +
∂t3
t1 t23
(t1 + t3 )
∂P
∂P
Airr 1
1
Airr
⇒
−
=
−
= 2 2 (t3 − t1 ) = 0
∂t1 ∂t3
t1 t3 t1 t3
t1 t3
⇒ t1 = t3
∂P
∆T ∆S Airr
1 Airr ∆T ∆S
⇒
=−
+ 3 = 2
−
=0
∂t1
4t21
t1
t1 t1
4
4Airr
⇒ t∗1 = t∗3 = 2t∗r =
∆T ∆S
(3.74)
(3.75)
Bereits in Kapitel 3.1.4 konnten wir zeigen, dass für t∗1 , t∗3 , bei denen die ersten partiellen
Ableitungen der Leistung nach den Zeiten t1 , t3 verschwinden, die Leistung maximal wird.
Wir erhalten die maximale Leistung wenn beide isothermen Zustandsänderungen die Zeit
benötigen, die in Gl.(3.75) berechnet wurde. Die Arbeit W ∗ , die Wärmeaufnahme vom
wärmeren Wärmereservoir Q(1) und der Wirkungsgrad η ∗ bei maximaler Leistung betragen:
Q(1)∗
η∗ =
1
∆T ∆S
2
1
(3Th + Tc ) ∆S
4
=
1
W ∗ = − ∆T ∆S
2
1
1
= Th ∆S − ∆T ∆S = (3Th + Tc ) ∆S
4
4
2 ∆T
2∆T
2ηC
ηC
Th
=
=
=
Tc
3Th + Tc
−ηC + 4
2 − 21 ηC
3 + Th
(3.76)
(3.77)
(3.78)
33
3 Durchführung
Die maximale Leistung selbst wird zu:
2

2
1
1
2
∆T ∆S
∆T ∆S
1
ln wb − ln wa
4
 4

∗
P =
= µ √
(∆T )2
√  = µ √
√
Airr
wb − wa
64
wb − wa
(3.79)
Die maximale Leistung skaliert mit P ∼ (∆T )2 und ist abhängig von der Mobilität µ und
den Randbedingungen der Varianzfunktion. Der erste Term in Gl.(3.79) kann bereits aus
(1)
(3)
Gl.(3.34) gewonnen werden, wenn man Airr = Airr setzt. Der Wirkungsgrad bei maximaler
Leistung in Gl.(3.78) ist unabhängig von den Randbedingungen der Varianzfunktionen. Der
Carnot-Wirkungsgrad ηC ist nur begrenzt durch das Temperaturverhältnis Tc /Th . Wenn
dieses Verhältnis gegen Null geht, dann geht der Carnot-Wirkungsgrad gegen 1. Dann
hat aber der Wirkungsgrad in Gl.(3.78) den maximalen Wert 2/3. Der Wirkungsgrad
in Gl.(3.78) wurde schon in Kapitel 3.1.4 gewonnen. Als Voraussetzung haben wir dort
eine isotrope und temperaturabhängige Mobilitätsmatrix festgestellt. Da diese spezielle
stochastische Wärmekraftmaschine in einem eindimensionalen Ortsraum arbeitet und
die Mobilität nicht temperaturabhängig gewählt wurde, sind die Voraussetzungen, damit
der Faktor γ = 12 in Gl.(3.35) gewählt werden kann, erfüllt. Somit bestätigt Gl.(3.79)
die allgemeinere Formel für den Wirkungsgrad in Gl.(3.35). Der Wirkungsgrad ηCA der
Curzon-Ahlborn-Maschine bei maximaler Leistung in Gl.(2.11) ist ein wichtiges Ergebnis
der endoreversiblen Thermodynamik. In [1] konnte gezeigt werden, dass in der linearen
irreversiblen Thermodynamik der Wert in Gl.(2.11) eine obere Grenze für den Wirkungsgrad
bei maximaler Leistung darstellt. Wir drücken nun den Wirkungsgrad ηCA aus durch den
Carnot-Wirkungsgrad ηC :
p
ηCA = 1 − 1 − ηC
(3.80)
In Abb.3.3 sind der Carnot Wirkungsgrad ηC , der Curzon-Ahlborn-Wirkungsgrad ηCA
und der Wirkungsgrad der stochastischen Wärmekraftmaschine η ∗ am Punkt maximaler
Leistung über dem Carnot-Wirkungsgrad aufgetragen. Der Curzon-Allborn-Wirkungsgrad
fällt mit dem Carnot-Wirkungsgrad bei minimalem und maximalen Carnot-Wirkungsgrad
zusammen. Der Wirkungsgrad der stochastischen Wärmekraftmaschine ist bei niedrigem
Carnot-Wirkungsgrad nahezu identisch mit dem Curzon-Ahlborn-Wirkungsgrad. Ab einem
Carnot-Wirkungsgrad von ungefähr 0.4 wächst der Curzon-Ahlborn-Wirkungsgrad schneller
als der Wirkungsgrad der stochastischen Wärmekraftmaschine.
34
3.2 Ein Kolloid in einem harmonischem Potential
1
η*
ηCA
ηC
0.8
η
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
ηC
Abbildung 3.3: Wirkungsgrad der stochastischen Wärmekraftmaschine η ∗ im Vergleich mit
dem Wirkungsgrad ηCA der Curzon-Ahlborn-Maschine und dem CarnotWirkungsgrad, am Punkt maximaler Leistung
35
3 Durchführung
36
4 Zusammenfassung und Ausblick
In dieser Arbeit wurden zunächst thermodynamische Größen auf der überdämpften FokkerPlanck-Gleichung definiert. Das erste wichtige Ergebnis ist der Ausdruck für die irreversible
Arbeit in Gl.(3.11). Dieser Ausdruck gilt universell für alle Prozesse, die sich mit der
überdämpften Fokker-Planck-Gleichung beschreiben lassen und die eine isotherme Zustandsänderung durchlaufen. Durch eine Transformation konnte die Gl.(3.11) so umgeformt
werden, dass es uns möglich war einen Ausdruck für die maximale Leistung in Gl.(3.34)
und den Wirkungsgrad bei maximaler Leistung in Gl.(3.35), welcher unabhängig von den
Randbedingungen der Fokker-Planck-Gleichung ist, anzugeben. Der Wirkungsgrad bei maximaler Leistung enthält lediglich noch einen Faktor, der abhängig ist von dem Verhältnis
der irreversiblen Wirkungen der beiden isothermen Zustandsänderungen im Kreisprozess.
Ist die Mobilitätsmatrix isotrop und temperaturunabhängig, so nimmt dieser Faktor den
Wert 12 an. Der hier berechnete Wirkungsgrad unterscheidet sich grundlegend von dem
Wirkungsgrad der Curzon-Ahlborn-Maschine bei maximaler Leistung, der als eine obere
Grenze in der makroskopischen endoreversiblen Thermodynamik gilt. Gerade für einen
großen Carnot-Wirkungsgrad ist der hier berechnete Wirkungsgrad deutlich geringer als
der Curzon-Ahlborn Wirkungsgrad. Der Grund sind unter anderem die hier auftretenden
thermischen Fluktuationen. Weiterhin haben wir uns hier nicht auf eine lineare Beschreibung
der irreversiblen Vorgänge beschränkt.
Als Beispiel haben wir uns danach eine stochastische Wärmekraftmaschine in einem harmonischen Potential angeschaut. Zunächst haben wir eine Differentialgleichung für die Varianz
des Teilchenortes hergeleitet, da diese Größe sehr wichtig für alle anderen thermodynamischen Größen war. Wir konnten danach Ausdrücke für die Entropie, die Arbeit und
die irreversible Arbeit finden. Mit Hilfe der Variationsrechnung konnten wir eine zeitliche
Steuerung des harmonischen Potentials finden, für die die irreversible Arbeit minimal
und somit die Arbeit im Kreisprozess maximal wurde. Die Ausdrücke für die maximale
Leistung und des Wirkungsgrades bei maximaler Leistung für dieses Biespiel bestätigten
die allgemeinen Ausdrücke.
Zu untersuchen bleibt die genaue Größe für die irreversiblen Wirkungen Airr für beliebige
Potentiale. Mit Hilfe der Theorie der optimalen Steuerung partieller Differentialgleichungen
könnte man für Potentiale mit vorgegebener Ortsverteilung die Zeitverteilung bestimmen,
für die die irreversiblen Wirkungen minimal werden. In diesem Fall kann man Ergebnisse
aber sehr wahrscheinlich nur noch mit numerischen Mitteln bestimmen. Die Frage ist, ob es
für eine weite Klasse von Ortsverteilungen des Potentials eine universelle untere Grenze der
irreversiblen Wirkungen gibt.
37
4 Zusammenfassung und Ausblick
38
Literaturverzeichnis
[1] Broeck, C. Van den: Thermodynamic Efficiency at Maximum Power. Physical
Review Letters, 95(190602), 2005.
[2] Hoffmann, K. H., J. M. Burzler und S. Schubert: Endoreversible Thermodynamics. Journal of Non-Equilibrium Thermodynamics, 22:311 –355, 1997.
[3] Nolting, Wolfgang: Grundkurs Theoretische Physik 4. Springer-Verlag Berlin
Heidelberg New York, 2003.
[4] Nolting, Wolfgang: Grundkurs Theoretische Physik 3, Kapitel 3.3 Magnetisches
Moment, Seite 176. Springer-Verlag Berlin Heidelberg New York, 2004. Hilfssatz 3.39.
[5] Schmiedl, Tim und Udo Seifert: Optimal finite-time processes in stochastic thermodynamics. Physical Review Letters, 98(108301), 2007.
[6] Schmiedl, Tim und Udo Seifert: Efficiency at maximum power: An analytically
solvable model for stochastic heat engines. Europhysics letters, 81, 2008. 20003.p120003.p6.
[7] Schwabl, Franz: Statistische Mechanik, Kapitel 3.2.2.3 Die Nichtintegrabilität von
δQ und δA, Seiten 86–87. Springer-Verlag Berlin Heidelberg New York, 2006.
[8] Schwabl, Franz: Statistische Mechanik, Kapitel 8. Brownsche Bewegung, Stochastische Bewegungsgleichungen und Fokker-Planck-Gleichungen, Seiten 417 – 428. SpringerVerlag Berlin Heidelberg New York, 2006.
[9] Seifert, Udo: Entropy production along a stochastic trajectory and an integral
fluctuation theorem. Physical Review Letters, 95(040602), 2005.
[10] Sekimoto, Ken: Langevin Equation and Thermodynamics. Progress of Theoretical
Physics, 130:17–27, 1998.
39