Lösung 10

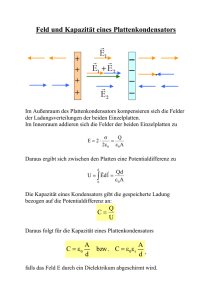
Physik II
Übung 10 - Lösungshinweise
Stefan Reutter
Moritz Kütt
Franz Fujara
SoSe 2012
Stand: 04.07.2012
Aufgabe 1 Lolli
Die kleine Carla hat von einem netten Onkel einen großen, runden Lolli geschenkt bekommen.
Da Carlas Mama ihr eingeschärft hat, dass sie keine Sachen von Fremden Männern annehmen
soll, oder, wenn doch, diese zumindest eingehend untersuchen soll, überprüft sie ihr Geschenk
zunächst mit einem Multimeter. Dabei stellt sie fest, dass der kugelförmige Lolli an seiner Oberfläche ein Potential von 450 V besitzt und in einem Abstand von 20 cm immerhin noch ein
Potential von 150 V. Nimm an der Lolli sei homogen geladen.
a) Wie groß ist der Radius des Lolli?
b) Wie groß ist die auf ihm befindliche Ladung?
c) Spielt es eine Rolle wie die Ladungen auf dem Lolli verteilt sind, also ob sie sich etwa nur auf
der Oberfläche befinden?
Natürlich schleckt das vorsichtige Mädchen nicht an dem geladenen Lolli. Stattdessen verwendet
sie ihn, um ihrem Papa einen Streich zu spielen. Erst danach macht sie sich genüsslich über die
Süßigkeit her.
Lösungshinweise:
Außerhalb der Kugel ist das elektrische Feld, wie wir schon mehrfach mit Hilfe des Gaußschen
Integralsatzes gezeigt haben, gleich dem einer Punktladung der gleichen Ladung im Mittelpunkt
der Kugel. Der Radius der Kugel sei R und d = 20 cm
a) Wir berechnen das elektrische Potential der Kugel
φ(R) =
φ(R + d) =
1
q
!
= U0 = 450 V
4πε0 R
q
1
!
4πε0 R + d
= U1 = 150 V
Dividiert man die erste Zeile durch die zweite ergibt sich
R+d
R
=
R=
U0
U1
d
U0
U1
−1
= 10 cm
1
Die Ladung erhält man, indem man dieses Ergebnis in eine der Gleichungen einsetzt
q = 4πε0 RU0 = 5 × 10−9 C
Aufgabe 2 Zylinderkondensator
Zwei lange leitende Zylindermäntel mit Radien R i < R a sind koaxial angeordnet. Der innere ZyR
lindermantel trägt eine Flächenladungsdichte σ, der äußere eine Flächenladungsdichte −σ R i .
a
Berechne für einen Teil der Zylinder mit Länge l
a) Die Spannung zwischen den Zylindern
b) Die Kapazität dieses Kondensators pro Längeneinheit
c) Die in ihm gespeicherte Energie pro Längeneinheit
Lösungshinweise:
Das Feld zwischen den Leitern muss aus Symmetriegründen radial nach außen zeigen. Integriert
man also über einen Zylinder der Länge l und Radius R i < r < R a muss das Feld auf seiner
Mantelfläche konstant sein während es auf den beiden Stirnseiten verschwindet.
Nach Gaußschem Integralsatz ergibt sich (siehe Übung 8, Aufgabe 7)
E=
σR i
ε0 r
Die Spannung erhält man aus der Potentialdifferenz zwischen innen und außen (Vorsicht Vorzeichen)
U=
ZR a
Edr =
σR i
ε0
ln
Ra
Ri
Ri
b) Die Kapazität pro Länge C ist definiert als
C=
=
Q
=
Ul
2πε0
ln
2πlR i σ
Ul
Ra
Ri
c) Die gespeicherte Energie ergibt sich analog zum Plattenkondensator zu
W=
Q2
2C l 2
=
πR2i σ2 ln
Ra
Ri
ε0
2
Aufgabe 3 Es fließt heraus und bleibt doch drinnen
Aus einer kugelförmigen Fläche mit dem Radius r = 12 cm wird ein elektrischer Fluss φ =
250 Vm ermittelt.
a) Welche Ladung muss sich im Inneren der Kugel befinden?
b) Wenn die Kugeloberfläche leitend ist, und die Ladung homogen auf ihr verteilt - wie groß ist
danan die Feldstärke direkt über der Oberfläche?
Lösungshinweise:
a)
φ=
I
~ · dA
~=
E
Q
"0
−9
Q = φ"0 = 2.2 × 10
C
b) Leitend bedingt homogen verteilt, das wiederum bedingt die Kugelsymmetrie des Problems.
Daher können wir den Betrag des Feldes über den Gauss’schen Satz ausrechnen, die Richtung
ist dann senkrecht zur Kugeloberfläche.
φ=
I
~ · dA
~
E
~ | · |A
~|
φ = |E
kV
φ
≈ 1.4
E=
2
m
4πr
Aufgabe 4 Dielektrikum im Plattenkondensator
Ein Plattenkondensator besteht aus zwei Platten mit einer Fläche von jeweils A = 500 cm2 . Die
Platten haben den Abstand d = 4 mm. Der Kondensator wird auf 100 V aufgeladen, anschließend von der Spannungsquelle getrennt.
a) Bestimme die elektrische Feldstärke zwischen den Platten und die Flächenladungsdichte auf
den Platten sowie die elektrostatische potentielle Energie.
Ein Dielektrikum (" r = 4) wird zwischen die Platten geschoben, es füllt den Raum zwischen den
Platten vollständig aus.
b) Wie groß ist nun die Feldstärke?
c) Wie groß ist die Potentialdifferenz zwischen den Platten?
d) Berechne die Flächenladungsdichte der gebundenen Ladungen (Ladungen an der Oberfläche
des Dielektrikums)?
3
Lösungshinweise:
a)
E=
U
= 25000
V
d
m
−7
σ = "0 E = 2.2 × 10 C/m2
1
1 "0 A 2
W = C U2 =
U = 1.1 × 10−6 J
2
2 d
b)
ED =
E
"r
= 6250
V
m
c)
U = E D d = 25 V
d)
σ
σ =σ b +
"
r 1
σ b =σ 1 −
= 1.66 × 10−7 C/m2
"r
Aufgabe 5 Dielektrizitäts-Hamburger
Ein Plattenkondensator mit der Kapazität C und dem Plattenabstand d wird mit zwei Dielektrika
("1 , "2 ) gefüllt. Jedes Dielektrikum hat eine Dicke d2 . Auf den Platten befinden sich die Ladungen
Q bzw. −Q.
d/2
d/2
ε1
ε2
a) Wie groß ist die elektrische Feldstärke in jedem Dielektrikum?
b) Wie groß ist die Potentialdifferenz zwischen den Platten?
c) Zeige, dass die Kapazität des gefüllten Kondensators durch folgende Formel gegeben ist:
Cd =
2"1 "2
"1 + "2
C
4
d) Zeige, dass man das System auch als zwei in Reihe geschaltete Kondensatoren betrachten
könnte.
Lösung:
a) Das elektrische Feld ohne Dielektrikum ist
E=
Q
Cd
Wir wissen, dass ein Dielektrikum das Feld wie folgt absenkt:
E
ED =
"r
Damit sind die beiden Felder
E D1 =
E D2 =
E
"1
E
"2
b) Die Differenz der Potentiale auf beiden Seiten eines Dielektrikums ist Ui = Ei · di . Für die
übereinanderliegenden Dielektrika müssen die beiden Potentialdifferenzen addiert werden. Damit ergibt sich
U = E D1
d
2
+ E D2
d
2
=
Q
1
"1
2C
+
1
"2
c) Wir berechnen direkt die Kapazität:
CD =
=
=
=
Q
U
Q
Q
2C
1
"1
+ "1
2
2
1 1
("
"1 "2 1
2"1 "2
"1 + "2
+ "2 )
C
C
5
d)
C D1 =2"1 C
C D2 =2"2 C
1
1 −1
CD =
+
C D1 C D2
−1
1
1
+
=
2"1 C 2"2 C
1
=C · 2 · 1
+ "1
"
=
2"1 "2
1
2
C
"1 + "2
Aufgabe 6 Nochmal ein Plattenkondensator
Ein Plattenkondensator mit der Fläche A, Plattenabstand d wird auf die Spannung U aufgeladen.
Anschließend wird er von der Spannungsquelle getrennt. Nun wird eine Platte mit der Fläche
A p = A2 und der Dielektrizitätszahl " r = 2 in den Kondensator eingeschoben.
A
d
εr
a) Weshalb muss das elektrische Feld im Dielektrikum und im freien Plattenzwischenraum den
gleichen Wert haben?
b) Zeige, dass die Ladungsdichte auf der Grenzfläche zwischen Leiter und Dielektrikum (σld )
genau doppelt so groß ist wie die auf der Grenzfläche Leiter - Luft (σl l ), also σl d = 2σl l .
c) Zeige, dass die neue Kapazität den Wert
3"0 A
2d
hat.
d) Zeige, dass die neue Spannung zwischen den Platten den Wert 23 U hat.
Lösungshinweise:
a) Jede Platte ist eine Äquipotentialfläche, da sie leitend ist. Zwischen den Platen muss daher
überall die gleiche Potentialdifferenz herrschen, auch dort wo das Dielektrikum ist. Da das Feld
in jeder Hälfte des Kondensators homogen ist, ergibt sich U = Ed und damit muss E auf beiden
Seiten gleich sein.
6
b) Für das Feld in der Nähe eines von einem Dielektrikum umhüllten Leiters (bzw. von einer
Seite umhüllt) gilt
σ
E=
" r "0
σ = E" r "0
Das Feld ist im ganzen Kondensator gleich, daher gilt für die Flächenladungsdichten
σ1 = E" r "0
σ2 = E"0
σ1 = 2σ2
c) Wir können den Kondensator als zwei parallelgeschaltete Kondensatoren betrachten. Die
Kapazität der einzelnen Kondensatoren wird dann einfach addiert.
C1 =
C2 =
" r "0 A2
d
"0 A2
d
C D =C1 + C2 =
"0 A
2d
(1 + " r ) =
3"0 A
2d
d) Der Kondensator hat die ganze Zeit die Ladungsmenge, die er zum Zeitpunkt der Aufladung
hatte. Diese ist
Q = Ca U =
"0 A
d
Die neue Spannung ist dann also
UD =
Q
CD
=
2Qd
3"0 A
=
2
3
U
Aufgabe 7 Diskussion: Der Ampèretiger
Wie ist die Definition des Ampère? Wie die des Coulomb? Warum ist das Ampere die Basiseinheit
und nicht das Kuhlomb?
Lösungshinweise:
Das Ampere ist die Stärke eines konstanten elektrischen Stroms, der, durch zwei parallele, geradlinige, unendlich lange und im Vakuum im Abstand von 1 Meter voneinander angeordnete Leiter
7
von vernachlässigbar kleinem, kreisförmigen Querschnitt fließend, zwischen diesen Leitern je 1
Meter Leiterlänge die Kraft 2 × 10−7 Newton hervorrufen würde.
Das Coulomb ist definiert als 1 Ampere × 1 Sekunde.
Eigentlich ist es viel sinnvoller, das Coulomb (d.h. die Ladung) als Basiseinheit zu definieren,
das auf Grund der Existenz der Elementarladung sehr gut definiert ist. In der Tat gibt es auch
Bestrebungen, das Ampere über den Ladungsfluss zu definieren. Die historische Definition geht
auf eine Zeit zurück, zu der man sich der Elementarladung nicht bewusst war.
Aufgabe 8 Diskussion: Das Alte Leiden
Was ist eine Leidener Flasche? Erkläre ihre Funktionsweise.
Lösungshinweise:
Bei einer Leidener Flasche handelt es sich um nichts anderes als einen simplen Kondensator. Zumeist ist es ein Glaszylinder, der beidseitig mit einer Metallschicht bedeckt ist. Das Glas fungiert
dabei als Isolator. Frühe Experimentatoren hatten es hierbei in erster Linie auf die Speicherung der elektrischen Ladung abgesehen: eine frühe Batterie bestand aus mehreren parallelen
Leidener Flaschen.
8