Winkelfunktionen/Trigonometrie: Lernziele I. Grundlagen: A. Sie

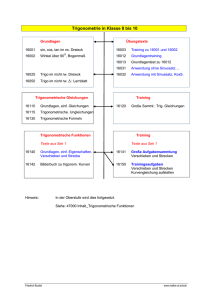
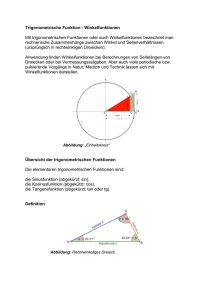
Mathematik
bla
Winkelfunktionen/Trigonometrie: Lernziele
I. Grundlagen:
A.
Sie können Winkel in Grad oder in Bogenlängen angeben.
B.
Sie kennen die Definition der Sinus-, Cosinus- und Tangensfunktion im rechtwinkligen Dreieck
und am Einheitskreis.
C.
Sie können Funktionswerte der Winkelfunktionen und ihrer Umkehrfunktionen mit dem
Taschenrechner berechnen.
D.
Sie kennen die Beziehungen zwischen den Winkelfunktionen (sinx) +(cosx) = 1 ,
tan x = sinx/cosx und können diese bei Termumformungen anwenden.
2
2
II. Winkelfunktionen
E.
Sie können die Graphen der Sinus-, Cosinus- und Tangensfunktion zeichnen.
F.
Sie können zu einer gegebenen Winkelfunktion die Periode und die Amplitude angeben.
G.
Sie können bei der Sinus- und der Cosinusfunktion die Wirkung der Parameter, welche die
Amplitude und die Periode beeinflussen (z.B. y = a sin(bx) ) , beschreiben und die
entsprechenden Graphen zeichnen, bzw. zu gegebenen Graphen den Funktionsterm
bestimmen.
H.
Sie können Winkelfunktionen in x-Richtung verschieben und erkennen die auftretenden
𝜋
Identitäten (z. B. cos (𝑥 − ) = sin⁡(𝑥) )
2
III. Trigonometrie
I.
Sie können Aufgaben mit Winkelberechnungen am rechtwinkligen Dreieck lösen.
J.
Sie können den Sinussatz und den Cosinussatz anwenden, um Berechnungen an beliebigen
Dreiecken durchzuführen.
IV. Trigonometrische Terme und Gleichungen
K.
Sie können mithilfe der Additionstheoreme und der Beziehungen unter D. trigonometrische
Terme umformen und vereinfachen.
L.
Sie verstehen, weshalb trigonometrische Gleichungen mehrere Lösungen haben.
M.
Sie können einfache trigonometrische Gleichungen lösen und die Ergebnisse in Grad oder
Bogenlängen angeben.
F:\1_GYMER\_Unterricht\AUFGABEN\03_4 Winkelfunktionen\Lernziele.docx
1