Suprafluidität und die Teilchenzahldarstellung von Bosonen

Suprauidität und die Teilchenzahldarstellung von
Bosonen
Alexander Schuckert
13. Januar 2015
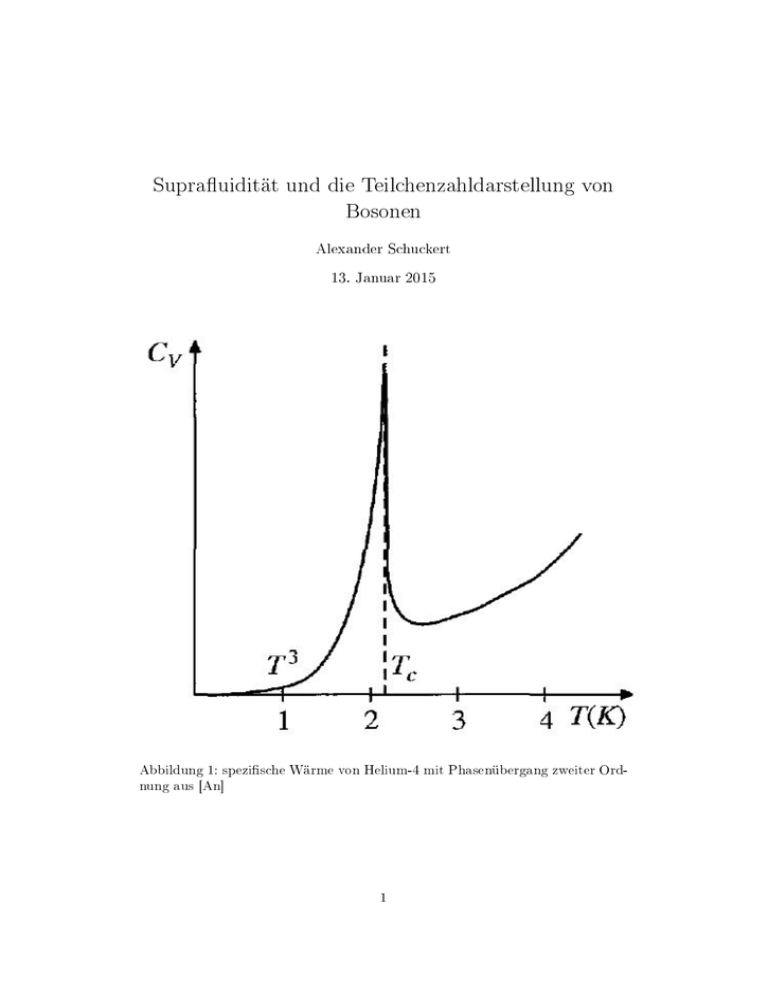
Abbildung 1: spezische Wärme von Helium-4 mit Phasenübergang zweiter Ordnung aus [An]
1
2
INHALTSVERZEICHNIS
Inhaltsverzeichnis
1 Einleitung
1.1 Historische Entwicklung . . . . . . . . . . . . . . . . . . . . . . .
3
3
2 Teilchenzahldarstellung von Bosonen
2.1 Motivation . . . . . . . . . . . . . . . . .
2.2 Der Fockraum . . . . . . . . . . . . . . .
2.3 Erzeugungs-und Vernichtungsoperatoren
2.4 Operatoren in zweiter Quantisierung . .
.
.
.
.
4
4
4
5
5
3 Das freie Bosonengas
3.1 Die spezische Wärme von He-4 und des idealen BECs . . . . . .
6
7
4 Das schwach wechselwirkende Bosegas
4.1 Anregungsspektrum von Helium und Suprauidität . . . . . . . .
8
10
5 Literaturverzeichnis
11
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1 EINLEITUNG
1
3
Einleitung
Diese Arbeit soll in das Phänomen der Suprauidität bei Helium-4 und die damit
verbundene Betrachtung der Bose-Einstein-Kondensation in der Teilchenzahldarstellung von Bosonen einführen. Dabei wird zunächst letztere eingeführt, bevor
dann durch die Betrachtung eines schwach wechselwirkenden Bosegases eine erste
Erklärung für das Phänomen der verschwindenen Viskosität bei Helium-4 gegeben werden kann.
1.1 Historische Entwicklung
Im Jahr 1925 sagte Albert Einstein die Bose-Einstein-Kondensation voraus. Dies
war das Ergebnis einer vorher geführten Korrespondenz mit Satyendranath Bose,
dem Einstein seine Arbeit zur Quantenstatistik der Photonen per Brief zusandte.
Einstein übernahm dessen Idee und wandte sie auch auf Atome an, nachdem er
dafür gesorgt hatte, dass Boses Arbeit unter dessen Namen veröentlicht wurde.
Knapp dreizehn Jahre später entdeckte Pyotr Leonidovich Kapitsa, dass üssiges
Helium 4 unterhalb von 2, 17K so gut wie keine Viskosität besitzt - die Suprauidität war entdeckt und wurde 1978 mit dem Nobelpreis belohnt. Dieser Eekt
wurde bald der bosonischen Natur von He-4 zugeschrieben.
Umso gröÿer war dann die Überraschung, als das gleiche Phänomen auch bei He3 festgestellt wurde, einem Fermion. Diese Entdeckung machten 1972 Oshero,
Lee und Richardson jedoch bei der um drei Gröÿenordnungen tieferen Temperatur von 2, 8mK. Die Erklärung hierfür liefert ein ähnlicher Mechanismus wie die
Bildung von Cooperpaaren in der Supraleitung - anstatt von Elektronen bilden
hier zwei He-3 Atome ein bosonisches Paar. Da die Paarwechselwirkung dieser
beiden Atome aber sehr schwach ist und bei höheren Temperaturen von der thermischen Energie der Atome überlagert wird, tritt die Suprauidität erst bei sehr
viel kleineren Temperaturen auf als bei He-4.
1995 wurde dann auch das erste Bose-Einstein-Kondensat im Labor erzeugt. Dies
wurde durch die von Steven Chu, Claude Cohen-Tannoudji und William Daniel
Phillips pionierten Methoden zur Kühlung von Gasen durch Laserkühlung möglich. An der Erzeugung des ersten BEKs war auch Wolfgang Ketterle, ein Alumni
der Universität Heidelberg beteiligt, der zusammen mit Eric Allen Cornell und
Carl Edwin Wieman für diese Leistung den Nobelpreis 2001 erhielt.
Helium-4 wird heute dank seiner einmaligen Eigenschaften auch in vielen technischen Anwendungen verwendet. Im Large Hadron Collider am CERN wird die
nahezu perfekte thermische Leitfähigkiet zur Kühlung der supraleitenden Magnete verwendet.
Desweiteren werden heute Bose-Einstein-Kondensate routinemäÿig in kalten Quantengaselabors in aller Welt erzeugt - unter anderem auch an der Universität Heidelberg in den Gruppen von Selim Jochim, Matthias Weidemüller und Markus
Oberthaler. Auch am MPI für Kernphysik wird die Bose-Einstein-Kondensation
untersucht.
2 TEILCHENZAHLDARSTELLUNG VON BOSONEN
2
4
Teilchenzahldarstellung von Bosonen
2.1 Motivation
Um ein Mehrteilchensystem von Bosonen(Teilchen mit ganzzahligem Spin) zu
beschreiben, ist eine neue Formulierung der Quantenmechanik nötig. Dieser Fakt
entsteht aus dem Umstand, dass in der Einteilchendarstellung der Quantenmechanik die Teilchenzahl immer erhalten ist, bei Mehrteilcheninteraktionen bei
hoher Energie jedoch Erzeugung und Vernichtung von Teilchen aufgrund der relativistischen Energie-Masse Äquivalenz möglich sein sollte.
Dieser Gedankengang führt zur sogenannten ÿweiten Quantisierung", die ihren
Namen durch den Umstand erhielt, dass in ihr nicht nur die quantenmechanischen Observablen quantisiert sind, sondern auch die Wellenfunktion an sich.
Dies markiert den Übergang zur voll relativistischen Quantenfeldtheorie, welche
in Gestalt des Standardmodells der Elementarteilchenphysik die erfolgreichste
mikroskopische Theorie der Physik liefert.
Zur Formulierung der Teilchenzahldarstellung sind zwei Postulate nötig:
• Zustände wechselwirkender Teilchen können in nichtwechselwirkende Ba-
siszustände expandiert werden.
• Die Mehrteilchenphysik wird vollständig durch die Gesetze der Elementar-
teilchenphysik beschrieben
Das erste Postulat bedeutet in der Sprache der Quantenfeldtheorie, dass der Vakuumzustand, also der Zustand, in dem keine Teilchen enthalten sind, tatsächlich
leer ist und keine Vakuumuktuationen enthält. In einer interagierenden Theorie
gilt dies jedoch nicht mehr und das erste Postulat ist nicht mehr gültig, da dann
insbesondere keine Modenexpansion der Felder in Auf-und Absteigeoperatoren
mehr möglich ist.
2.2 Der Fockraum
In der zweiten Quantisierung wird die Wellenfunktion durch die Besetzungszahlen
der Eigenzustände eines Operators charakterisiert.
|Ψi = |n0 , n1 , ...i
(1)
Wobei die ni die Besetzungszahlen des i-ten Eigenzustands kennzeichnen.
Die Gesammtteilchenzahl ist dabei gegeben durch
∞
X
ni
(2)
i=0
Das Vakuum wird dabei als Zustand deniert, in dem keiner der Eigenzustände
besetzt ist:
|0i = |0, 0, ...i
(3)
2 TEILCHENZAHLDARSTELLUNG VON BOSONEN
5
Für Fermionen gilt wegen des Paulisches Aussschlussprinzips: nFi ermion ∈ {0, 1}
Diese Einschränkung gilt für Bosonen nicht: nBoson
∈N
i
Da die Bose-Einstein-Kondensation auf einer groÿen Besetzung des Grundzustandes beruht ist daher kein vergleichbares Phänomen bei Fermionen beobachtbar.
2.3 Erzeugungs-und Vernichtungsoperatoren
Um nun die Teilchenzahl modizieren zu können, werden der Erzeugungsoperator a† und der Vernichtungsoperator a eingeführt. Ihre Wirkung auf die i-te
Besetzungszahl ist dabei wie folgt:
a†i |n0 , ..., ni , ...i =
√
ai |n0 , ..., ni , ...i =
ni + 1 |n0 , ..., ni + 1, ...i
(4)
√
(5)
ni |n0 , ..., ni − 1, ...i
Die Normierung impliziert dabei die Dention des Teilchenzahloperators:
Ni = a†i ai
(6)
Man kann sich schnell auch von den für die beiden Operatoren geltenden Kommutatorrelationen
[a†i , a†j ] = 0 = [ai , aj ]
(7)
[ai , a†j ] = δij
(8)
überzeugen. Diese Kommutatorrelationen sind gleichzeitig denierende Eigenschaft von Bosonen. Für Fermionen gelten die gleichen Beziehungen als Antikommutatoren.
2.4 Operatoren in zweiter Quantisierung
Die Konstruktion diagonaler Operatoren erfolgt durch Zählen der Teilchen in den
Eigenzuständen des Operators, multipliziert mit dem Eigenwert und summiert
über alle Zustände. Für einen diagonalisierten Hamiltonoperator gilt dann
H=
∞
X
Ei a†i ai .
(9)
i=0
Desweiteren kann man zeigen, dass sich Einteilchen- bzw. Zweiteilchenoperatoren
aus den Einteilchenmatrixelementen mit Potenzial v wie folgt ergeben:
VEinteilchen =
X
hi|v|ji a†j ai
(10)
i,j
VZweiteilchen =
1 X
hi, j|v|k, mi a†i a†j ak am
2
(11)
i,j,k,m
Die hier präsentierte Methode kann nun verwendet werden, um ein freies Bosonengas zu betrachten.
6
3 DAS FREIE BOSONENGAS
3
Das freie Bosonengas
In einem Gas nichtinteragierender, nichtrelativistischer Bosonen sind die Eigenenergien durch die kinetische Energie geben:
Ek =
(h̄k)2
2m
(12)
Der Hamiltonoperator ist dann nach Gleichung 9 in Impulsdarstellung gegeben
durch:
∞
H=
(13)
Ek a†k ak
X
k=0
Die Besetzungszahlen sind dabei gegeben durch die Bose-Einstein-Verteilung, die
aus der Quantenstatistik zu
1
nk =
exp
Ek −µ
kB T
(14)
−1
∂U
bestimmt ist. µ = ∂N
kennzeichnet dabei das chemische Potential, welches als
Ableitung der freien Energie nach der Gesamtteilchenzahl deniert ist. Anschaulich ist µ die Energie, die dem System bei Hinzufügen eines Teilchens gegeben(oder abgezogen) wird.
Integriert man obige Verteilung über alle Impulse und betrachtet das Verhalten
des chemischen Potentials mit der Temperatur, so stellt man fest, dass es eine
kritische Temperatur Tc gibt, für die das chemische Potential verschwindet. Sie
kann zu
2
Tc =
2πh̄2
kB m
n
2, 612
3
(15)
bestimmt werden. Für Helium-4 beträgt diese kritische Temperatur 3,1K, was
schon in der gleichen Gröÿenordnung wie der Phasenübergang bei 2,17K liegt,
wenn auch noch 50% daneben.
Betrachtet man nun die Besetzung des Grundzustandes
n0 =
1
exp − kBµT
,
−1
(16)
so erkennt man, dass diese für µ− > 0 gegen unendlich geht. Der Grundzustand
wird also für T − > Tc makroskopisch besetzt. Man sagt die Teilchen kondensieren
aus. Der Anteil der sich im Grundzustand bendlichen Teilchen für Temperaturen
kleiner Tc ist dabei durch
n0
=1−
N
gegeben.
T
Tc
2
3
(17)
3 DAS FREIE BOSONENGAS
7
3.1 Die spezische Wärme von He-4 und des idealen BECs
Nicht nur die kritische Temperatur und die Phasenübergangstemperatur von He4 und des idealen BECs passen nicht so recht zusammen. Auch die Gestalt des
Phasenübergangs unterscheidet sich. Dies lässt sich am besten am Verlauf der
spezischen Wärmen erkennnen. Man erkennt, dass das ideale Bose-EinsteinKondensat keine gute Beschreibung suprauiden Heliums ist. Dies ist aber eigentlich recht leicht ersichtlich, da in Helium die zwischenatomaren Kräfte recht
stark sind und daher Wechselwirkungen nicht vernachlässigt werden können. Dies
soll nun im Folgenden besser gemacht werden.
Abbildung 2: Die spezische Wärme von He-4. Die charakteristische Form wie
der griechische Buchstabe λ war der Ursprung der Bezeichnung dieses Vorgangs
als λ -Übergang. Bei der Phasenübergangstemperatur divergiert die spezische
Wärme, was der deninierenden Eigenschaft eines Phasenübergangs 2.Ordnung
nach Ehrenfest entspricht., aus [An]
Abbildung 3: Die spezische Wärme eines idealen Bose-Einstein-Kondensats. Bei
der kritischen Temperatur ist sie nicht stetig dierenzierbar, die denierende
Eigenschaft eines Phasenübergangs 3.Ordnung, aus [An]
8
4 DAS SCHWACH WECHSELWIRKENDE BOSEGAS
4
Das schwach wechselwirkende Bosegas
Wir erweitern den in Gleichung 9 dargestellten freien Hamiltonoperator mit einer
Zweiteilchenwechselwirkung. Die in Gleichung 11 dargestellte Form des Potentials
wird noch fouriertransformiert:
H=
X k2 †
1 X
bk bk +
Vq b†k+q b†k−q bp bk
2m
2V
k
(18)
k,p,q
Dabei ist m die Masse der RTeilchen, V das Volumen, q der Impulsübertrag der
Wechselwirkung und Vq = d3 xe−iqx V (x) die Fouriertransformierte des ortsabhängigen Potentials.
Das Ziel der nun folgenden Rechnung ist, den Hamiltonoperator auf eine Diagonalform zu bringen und dabei den rechts stehenden Wechselwirkungsterm auszuwerten.
Dabei wird extensiv die Annahme ausgenutzt, dass trotz der Wechselwirkung
eine Bose-Einstein-Kondensation stattndet, ab einer bestimmten Temperatur
also für die Besetzung n0 des Grundzustandes gilt:
(19)
n0 ≈ N
Die erste Näherung, die nun gemacht werden kann ist, dass die Wechselwirkung
von Teilchen mit k 6= 0 untereinander vernachlässigt werden kann. Es werden
also nur Wechselwirkungen von kondensierten Teilchen untereinander und von
kondensierten mit nichtkondensierten berücksichtigt.
Desweiteren kann auch für die Auf-und Absteigeoperatoren des Grundzustandes
wie folgt genähert werden:
b†0 |N0 , ...i =
p
p
N0 + 1 |N0 + 1, ...i ≈ N0 |N0 , ...i
p
p
b0 |N0 , ...i = N0 |N0 + 1, ...i ≈ N0 |N0 , ...i
Wodurch direkt
(20)
(21)
(22)
[b0 , b†0 ] = 0
folgt. Die√Wirkung der beiden Operatoren kann nun also einfach als Multiplikation mit N0 betrachtet werden.
Es können nun in der Summe des Wechselwirkungsterms nur noch folgende Fälle
auftreten:
1. Alle Impulse sind null
2. Drei Impulse sind null: Auf Grund von Impulserhaltung nicht möglich
3. Zwei Impulse sind null: Dafür gibt es
= 6 Möglichkeiten
√
4. Ein Impuls ist null: Dieser Term ist von der Ordnung N0 und kann ver-
nachlässigt werden
4
2
4 DAS SCHWACH WECHSELWIRKENDE BOSEGAS
Fall 1 trägt einen Term
9
V0 N02
2V
(23)


X
N0  X
2
[V0 + Vk ]b†k bk +
Vk (b†k b†−k + bk b−k )
2V
(24)
bei, wohingegen Fall 3 folgendes beiträgt:
k6=0
k6=0
Nun kann auch noch die Grundzustandsbesetzung durch die Gesamtteilchenzahl
ausgedrückt werden:
X †
bk bk
(25)
N = N0 +
k6=0)
=>
N02
2
= N − 2N
X
b†k bk +
b†k bk b†k0 bk0
X
(26)
k,k0 6=0
k6=0
Der letzte Term ist dabei von der Ordnung (N − N0 )2 und kann daher vernachlässigt werden. Einsetzten von 26 in 23 von N0 ≈ N in 24 und anschlieÿendes
Einsetzen von 23 und 24 in den Hamiltonian liefert:
H=
X k2 †
V0 N 2 N X
N X
bk bk +
+
Vk b†k bk +
Vk (b†k b†−k + bk b−k )
2m
2V
V
2V
k
k6=0
(27)
k6=0
Der nun verbleibende Nichtdiagonalterm(der ganz rechte) kann nun beseitigt
werden, in dem man einen neuen Auf-und Absteigeoperator βk bzw. βk† und zwei
reelle Funktionen uk und vk einführt, sodass für die alten Operatoren gilt:
Daraus folgt
†
bk = uk βk − vk β−k
(28)
b†k = uk βk† − vk β−k
(29)
(30)
Setzt man diesen Ansatz in den Hamiltonian 27 ein, so erhält man eine zweite
Bedingung für die uk und vk unter der der Hamiltonian diagonal wird.
Unser Endergebnis lautet dann:
u2k − vk2 = 1
X
V0 N 2 1 X k 2
N Vk
H=
−
+
+ Ek +
Ek βk† βk
2V
2
2m
V
k6=0
k6=0
{z
} |
{z
}
|
Grundzustandsenergie
(31)
Quasiteilchen
Das neue Vakuum ist dabei das Vakuum der Quasiteilchenanregung. Diese haben
die Energie
Ek =
k2
2m
2
N k 2 Vk
+
Vm
!1
2
.
(32)
Für kleine k kann diese Energie linear genährt werden:
r
Ek ≈
V0
k
Vm
Die Quasiteilchen sind also für kleine k Phononen mit linearer Dispersion.
(33)
4 DAS SCHWACH WECHSELWIRKENDE BOSEGAS
10
4.1 Anregungsspektrum von Helium und Suprauidität
Abbildung 4: Das Anregungsspektrum von Helium-4 zeigt tatsächlich für kleine
k ein lineares Dispersionsspektrum. Für gröÿere k entsteht jedoch ein lokales
Minimum. Dieses wird durch das von Landau entwickelte Rotonenmodell erklärt,
für das er 1962 den Nobelpreis erhielt, aus [An]
Diese Vorhersage kann nun mit dem Anregungsspektrum von Helium verglichen werden. Mit der linearen Dispersionsrelation kann man nun die Suprauidität unter folgender Überlegung erklären:
Betrachte ein sich durch die Flüssigkeit bewegendes makroskopisches Objekt mit
Impuls P = M ∗ v und Energie E = 12 ∗ M ∗ v 2 . Dieses wird nun bei Durchgang
durch die Flüssigkiet nur dann abgebremst, indem es Phononen anregt. Nach der
Anregung hat das Objekt die neue Geschwindigkeit
v0 = v −
h̄k
M
(34)
und die neue Energie
1
h̄k 2
1
E 0 = M v 02 = M (v −
) ≈ E − h̄kv
2
2
M
(35)
Für die Energiedierenz muss aber auch gelten:
!
∆E = E − E 0 = h̄vk = Ek = h̄ck
(36)
Daraus folgt nun, dass eine Phononenanregung nur für Objektgeschwindigkeiten
v > c möglich ist. Das schwach wechselwirkende Bosegas also für Fieÿgeschwindigkeiten kleiner der Schallgeschwindigkeiten suprauide ist. Für Helium-4 beträgt diese c ≈ 60 ms .
11
5 LITERATURVERZEICHNIS
5
Literaturverzeichnis
Literatur
[La] Landau,Lifshitz: Quantum Mechanics
[An] James F.Annett: Superconductivity, Superuids, Condensates
[Schw] Franz Schwabl: Quantenmechanik für Fortgeschrittene
[Mu] A.Muramatsu:
Fortgeschrittene
Quantenmechanik
http://www.
itp3.uni-stuttgart.de/lehre/Archiv/Courses_upto_ss13/
Fortgeschrittene_Quantentheorie_WS_2011.2012/Kapitel5.pdf