6 Partiell geordnete binäre Bäume: Heap (Haufen) Motivation Heap

6 Partiell geordnete binäre Bäume: Heap (Haufen)
Motivation
für manchen Anwendungen nur partielle Ordnung der
Elemente statt vollständiger nötig, z.B.
Prioritätsschlange: nur das minimale (oder maximale)
Element
k Maximalwerte aus Menge mit n >> k Elementen
(Rangfolgebestimmung von Suchmaschinen!)
Die typische Operationen:
Achtung, nicht mit
enqueue()
"Freispeicher-Halde"
findMin()
("heap")verwechseln!!
-
dequeueMin()
Gesucht Datenstruktur, die alle Operationen auch im
schlechtesten Fall in logarithmischer Zeit O(log n) ausführt
Verschiedene Realisierungen, hier binärer Heap
hs / fub – alp3-24-Heap 1
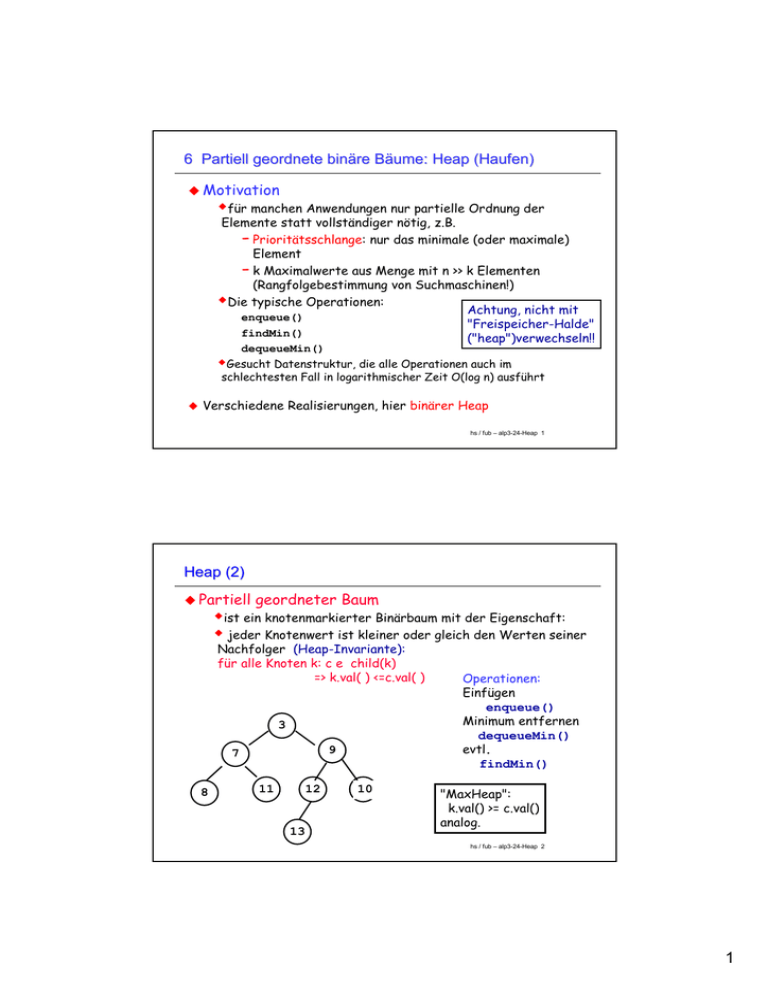
Heap (2)
Partiell
geordneter Baum
ist ein knotenmarkierter Binärbaum mit der Eigenschaft:
jeder Knotenwert ist kleiner oder gleich den Werten seiner
Nachfolger (Heap-Invariante):
für alle Knoten k: c e child(k)
=> k.val( ) <=c.val( )
3
9
7
8
11
12
13
10
Operationen:
Einfügen
enqueue()
Minimum entfernen
dequeueMin()
evtl.
findMin()
"MaxHeap":
k.val() >= c.val()
analog.
hs / fub – alp3-24-Heap 2
1
Binärer Heap
Logarithmische
3
Laufzeit?
Kann Baum entarten?
9
4
3
JA
6
5
12
10
4
13
5
Ziel:
Baum möglichst ausgeglichen
halten
z.B. Binominal Heap, Fibonacci Heap
hier: Binärer Heap
hs / fub – alp3-24-Heap 3
Binärer Heap
Zusätzliche
Strukturinvariante:
Fast vollständiger binärer Baum
4
5
6
15
16
9
25
14
7
12
11
h
20
8
Höhe h : 2h <= n < 2h+1 => h <= log n
Einige Beispiele aus Goodrich/ Tamassia (s. Lit.-Liste)
hs / fub – alp3-24-Heap 4
2
Beispiel
Kein
binärer Heap
4
5
6
13
15
16
25
14
7
12
11
20
8
hs / fub – alp3-24-Heap 5
Binäre Heaps
Kein
binärer Heap
4
5
6
9
15
16
25
14
7
12
11
20
8
hs / fub – alp3-24-Heap 6
3
Binärer Heap
Einfügen
(enqueue)
1 3
2
4
5
8
8 13
9
7
11
9
17
6
18
3
10 7
12
(i) vollständiger Baum
=> Knoten hier einfügen
2
10
(ii) Heap-Eigenschaft
wiederherstellen
hs / fub – alp3-24-Heap 7
Binärer Heap
enqueue()
1 3
2
4
8 13
5
8
11
9
9
7
2
18
6
12
3
10 7
17
10
while (parent > val) {exchange();}
("upheap")
O(log n) Vertauschungen
hs / fub – alp3-24-Heap 8
4
Binärer Heap
Vollständiger
Baum: Feldrepräsentation
1 3
2
4
3
0
5
8
8 13
1
9
7
13
11
9
17
3
10 7
12
6
18
10
7
9
8
2
3
4
17 12
5
6
10
7
13 11 18
8
9
10...
15
Reguläre Struktur: Nachfolger des Knoten i sind die Knoten 2*i
und 2*i+1, Vorgänger von i : i/2 
hs / fub – alp3-24-Heap 9
Imperative Implementierung
public class VectorHeap implements... {
// model:
// data Ord t => POTree t = E | N(POTree t) t (POTree t)
// inv E = True
// inv(N l x r) = (if l /= E then x<=root l else True) &&
(if r /= E then x<=root r else True) &&
inv l && inv r
//
&& and POTree is complete.
Object [] vheap;
// the array implementing the tree
private int size;
//number of nodes
private int length;
//a.length
private int current;
// the current node
private final int ROOT = 1;
// the root
hs / fub – alp3-24-Heap 10
5
Binary heap:
heap: enqueue
public void enqueue(Comparable val) throws
java.lang.Exception {
// requires : // effects: inserts val into this as a leaf into the
// only possible position which maintains completeness
// of tree and maintains heap invariant
// if count > size throws an execption
if (sizet== vheap.length -1) throw new
java.lang.Exception("heap full");
size++;
int i = size;
while (i > 1 && vheap[parent(i)].compareTo(val)>0)
{ vheap[i] = vheap[parent(i)];
i = i/2;
}
vheap[i] = val;
}
hs / fub – alp3-24-Heap 11
Binärer Heap:
Heap: dequeue
Minimum entfernen.
dequeue
1 2
2
4
8 13
5
8
11
9
9
3
7
17
6
12
3
10 7
1) Inv. "fast
vollständig" herstellen:
-> letztes Element als
Wurzel.
2) Heap-Invariante
herstellen.
18
10
muss hier entfernt (Vollständigkeit)
und passend eingefügt werden (Heap-Eigenschaft)
hs / fub – alp3-24-Heap 12
6
Beispiel: dequeue
2
1
2
4
8 13
9
3
5
8
11
9
18
7
6
3
10 7
12
17
10
hs / fub – alp3-24-Heap 13
Beispiel: dequeue
1
3
2 18
4
8 13
5
8
11
9
9
7
6
12
3
solange ein Kind mit
kleinerem Wert existiert:
Tausche mit kleinerem
der Kinder.
10 7
17
10
hs / fub – alp3-24-Heap 14
7
"downheap"
downheap"
1
2
4
8 13
9
7
5
8
11
9
3
18
6
3
10 7
12
17
10
hs / fub – alp3-24-Heap 15
Beispiel
1
2
4
8 13
11
9
9
7
5
8
3
17
6
12
3
10 7
18
10
hs / fub – alp3-24-Heap 16
8
Binärer Heap:
Heap: dequeue
Noch
ein Beispiel
1
2
4
8 13
7
4
5
5
6
6
12
3
10 7
10
11
9
3
10
hs / fub – alp3-24-Heap 17
3
1
4
2 5
4
8 13
7
5
10
6
6
12
3
10 7
11
9
10
Tauschoperationen: 10 <-> 3, 4 <-> 10, 5 <-> 10
hs / fub – alp3-24-Heap 18
9
Binärer Heap
Laufzeit:
enqueue() und dequeue():
findMin() :
Sortieren
O(log n)
O(1)
mit Heap: n*log n Operationen.
Konstruktion
eines Heap: n log n Schritte.
Geht das bessser?
Ja
hs / fub – alp3-24-Heap 19
Konstruktion eine Heap mit n = 2k Elementen
(n+1)/2 Elemente zu Heap-Knoten machen.
hs / fub – alp3-24-Heap 20
10
n+1 / 4 Elemente hinzunehmen zu n-1/4 heaps
verschmelzen.
Heap-Eigenschaft
herstellen (downheap)
1
2
1) enqueue(9)
2) enqueue(8)
enqueue (14)
11
HeapHeap-Konstruktion
"Bottom-up"-Konstruktion
benötigt O(n) Schritte.
(n+1)/2 Knoten einfügen
(n+1)/4 Knoten einfügen und downheap
(n+1)/8 Knoten einfügen und downheap
.....
n Einfügeoperationen, n/2 upheaps => O(n)
hs / fub – alp3-24-Heap 23
12