Statistische Analyse von Messergebnissen

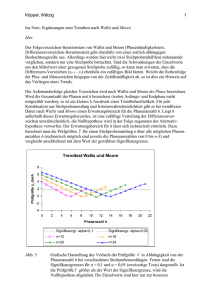
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
Stand: 17.02.2003
Seite 1 / 8
Im Abschnitt "Grundlagen der Statistik" wurde u.a. beschrieben, wie nach der Durchführung
eines statistischen Experiments, beispielsweise einer textilen Prüfung die gewonnenen
Daten ausgewertet werden. Man berechnet zunächst statistische Kenngrößen wie Mittelwert,
Median (zur Lagebestimmung), Varianz, Standardabweichung und Variationskoeffizient (zur
Bestimmung der Streuung) sowie Vertrauensbereiche und untersucht für die Daten, falls
mehrere Merkmale erfasst wurden, Korrelation und Regression. Hinzu kommt
– vgl. den Abschnitt "Grafische Darstellung und Interpretation von Messergebnissen" - in der
Regel eine grafische Darstellung der Ergebnisse (z.B. Histogramm, Boxplot).
Mit Hilfe der so gewonnenen Daten lassen sich weitere Kenntnisse über die geprüfte Grundgesamtheit durch statistische Tests und Analysen gewinnen. Im Vordergrund stehen hier
einerseits Vergleiche von Stichprobenparametern mit Soll- oder Erfahrungswerten. Andererseits werden Parameter verschiedener Messreihen miteinander verglichen.
Auf weitere sogenannte parameterfreie Tests gehen wir an dieser Stelle nicht ein.
Aus den Stichprobenparametern berechnet man zunächst sogenannte Test- oder Prüfgrößen unter der Annahme, dass die der Berechnung zugrundeliegende Zufallsvariable ähnlich wie bei der Berechnung der Vertrauensbereiche - eine bestimmte Verteilung besitzt.
Dann werden Prüfhypothesen formuliert, die mathematisch meist Ungleichungen sind, die
auf einen Vergleich der Prüfgröße mit Quantilen der entsprechenden Verteilung
hinauslaufen, und diesen eine Alternative gegenübergestellt. Die Nullhypothese wird mit H0
bezeichnet, die Alternativhypothese mit HA. Dabei wird die Alternativhypothese so formuliert,
dass immer entweder H0 oder HA zutrifft.
Durch den konkreten Vergleich von Prüfgröße und Quantil wird zwischen beiden Hypothesen
entschieden. Dabei wird ähnlich wie bei der Berechnung der Vertrauensbereiche
vrogegangen, d.h. man verwendet c2-, t- oder F- Verteilung. Hierbei können zwei Arten von
Fehlern auftreten:
Fehler 1. Art: Die Nullhypothese wird abgelehnt, obwohl sie richtig ist.
Fehler 2. Art: Die Nullhypothese wird beibehalten, obwohl sie falsch ist.
Man muss darauf achten, dass die Nullhypothese so formuliert ist, dass sie exakt geprüft
werden kann. In der Regel wird man die den Ausnahmefall beschreibende Hypothese als
Alternative formulieren.
Die Wahrscheinlichkeit α dafür, eine richtige Nullhypothese abzulehnen, wird vorgegeben. α
heißt daher Irrtumswahrscheinlichkeit oder Signifikanzniveau.
Mit β bezeichnet man hingegen die Wahrscheinlichkeit für einen Fehler zweiter Art. 1-β nennt
man auch die Power des entsprechenden Tests.
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
Stand: 17.02.2003
Seite 2 / 8
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
Damit sind folgende Szenarien möglich:
Entscheidung
des Tests
Realität:
H0 ist richtig
HA ist richtig
H0 wird beibehalten
Richtige Entscheidung mit
Wahrscheinlichkeit
1-α
Fehler 2. Art mit
Wahrscheinlichkeit β
H0 wird abgelehnt
Fehler 1. Art
Signifikanzniveau α
Richtige Entscheidung
mit der Power
1-β
In der Praxis ist es in der Regel schwierig, die beiden Fehlerwahrscheinlichkeiten optimal
aufeinander abzustimmen. Unmittelbar beeinflusst man nur den Fehler erster Art, da man
das Signifikanzniveau α vor der Durchführung eines Tests festzulegen hat.
1.)
Tests für den Mittelwert
Möchte man bei der Herstellung eines Produkts einen bestimmte Eigenschaft erreichen, z.B.
dass ein Garn eine bestimmte Feinheit besitzt, so wird man eine Stichprobe aus der
Produktion prüfen und den Mittelwert mit dem gewünschten Sollwert (oder einem
Erfahrungswert) x0 vergleichen. Weicht der Stichprobenmittelwert vom Sollwert ab, was
normalerweise der Fall ist, so wird man wissen wollen, ob man diese Abweichung als zufällig
hinnehmen kann (Nullhypothese) oder nicht. Hierzu führt man folgenden Test durch:
Man vergleicht die Prüfgröße, das ist die mit dem Kehrwert des Standardfehlers für den
Mittelwert gewichtete Differenz, für
a. kleine Stichproben (Umfang kleiner als 50) mit Quantilen der t-Verteilung
b. große Stichproben (Umfang größer oder gleich 50) mit Quantilen der
Standardnormalverteilung
Im ersten Fall spricht man von einem t-Test , im zweiten von
einem G(auss)-Test.
Unter einem Quantil versteht man in Abhängigkeit von α den
Wert, den die Zufallsvariable mit der Irrtumswahrscheinlichkeit α unterschreitet.
Flächeninhalt = α
1
0.5
Dazu gibt man sich eine Irrtumswahrscheinlichkeit α (meist
5%) vor und bestimmt aus Tabellen (oder Tabellenkalkulationsprogrammen) die zugehörigen Quantile, die im Falle der
2
t-Verteilung auch noch von den Freiheitsgraden (hier Stichprobenumfang –1) abhängen.
Quantil der Standardnormalverteilung: uα
0
x
2
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
Stand: 17.02.2003
Seite 3 / 8
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
Es kommt nun darauf an, ob der Sollwert eingehalten oder lediglich nicht unter- bzw.
überschritten werden darf. Im ersten Fall lautet die Nullhypothese µ = x0 . Man führt einen
zweiseitigen Test durch, d.h. für den Sollwert x0 berechnet man die Prüfgröße und prüft, ob
sie zwischen zwei Quantilen liegt:
x − x0
s
n ≤ tn−1;1− α / 2 bzw.
x − x0
n ≤ u1−α / 2 .
s
Die Betragsfunktion im Zähler sichert die zweiseitige Abgrenzung, da tn-1;α = -tn-1;1-α.
Ansonsten reicht ein einseitiger Test:
x − x0
x − x0
n ≤ tn−1;1−α bzw.
n ≤ u1− α , falls die Nullhypothese x ≤ x 0 lautet, oder
s
s
x − x0
x − x0
n ≥ tn−1; α bzw.
n ≥ uα , falls die Nullhypothese x ≥ x 0 lautet.
s
s
Sind die Ungleichungen nicht erfüllt, so wird die Nullhypothese verworfen, man geht davon
aus, dass die Alternativehypothese (hier das Gegenteil) anzunehmen ist.
2.)
Test für Varianz und Standardabweichung
Auch für die Varianz bzw. die Standardabweichung, die beispielsweise die Gleichmäßigkeit
eines Garns beschreiben, geht man ähnlich wie beim Mittelwert vor. Man vergleicht für eine
einen Sollwert s 0 die Prüfgröße (n − 1)
s2
mit den Quantilen der χ 2-Verteilung. (χ 2 –Test)
2
s0
Zweiseitiger Test zur Nullhypothese σ = s 0: χ
2
n −1; α / 2
s2
≤ (n − 1) 2 ≤ χ2n−1;1− α / 2
s0
Einseitiger Test zur Nullhypothese σ ≥ s 0: χ2n −1; α ≤ (n − 1)
s2
s20
s2
σ ≤ s 0: (n − 1) 2 ≤ χ2n−1;1− α
s0
Beispiel:
Drehungsmessung an einem Viskosekreppgarn:
Probe Nr.
Drehungen
pro 500mm
x = 1105,2
1
2
3
4
1090 1110 1125 1050
x − µ0
30.95
6
7
8
1057 1110 1141 1136
α = 5%
s = 30.95
Nullhypothese: µ0 =1108, Prüfgröße:
5
9
10
1123 1110
t9;0.975 = 2.26
10 = 0.286 . Der t-Test liefert:
Die Prüfgröße ist kleiner als das t-Quantil also wird die Nullhypothese nicht verworfen.
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
Stand: 17.02.2003
Seite 4 / 8
2
Für die Standardabweichung liefert der χ -Test mit s = 30.95 und α = 1% sowie den
2
2
Quantilen χ 9;0.005 = 1,73 bzw. χ 9;0.995 = 23.58 zur Nullhypothese σ0 = 35 wegen der
Prüfgröße: 9
3.
957.9
= 7,04 dass die Nullhypothese nicht verworfen werden darf.
1225
Vergleichstests:
Diese Gruppe von Tests beschäftigt sich mit dem Vergleich der Ergebnisse zweier
Stichproben, beispielweise wenn die Produktionsergebnisse mehrerer Maschinen oder
verschiedener Tage verglichen werden sollen. Auf Vergleiche von Parametern von drei und
mehr Stichproben im Rahmen der Varianzanalyse gehen wir hier nicht ein.
Zum Vergleich zweier Varianzen führt man einen F-Test durch. Die Prüfgröße ist der Quotient der Varianzen, der zwischen den entsprechenden F-Quantilen liegen muss, damit die
Nullhypothese: "Die Varianzen (bzw. Standardabweichungen) sind gleich." beibehalten wird.
Die F-Quantile hängen neben der Irrtumswahrscheinlichkeit von den jeweiligen Stichprobenumfängen n1 der ersten und n2 der zweiten Stichprobe ab. Es ist zu prüfen, ob
fn1−1;n2 −1;α / 2
s12
≤ 2 ≤ fn1 −1;n 2 −1;1−α / 2 gilt. Die Power des Tests erhöht sich, wenn man die größere
s2
der Varianzen in den Zähler setzt und nur die Nullhypothese σ1 ≤ σ2 prüft. Wenn diese nicht
verworfen wird, ist die Gleichheit der Varianzen nicht widerlegt, d.h. wenn gilt:
s12
≤ fn1 −1;n2 −1;1−α (einseitiger F-Test).
s22
Kann die Gleichheit der Varianzen nicht widerlegt werden, so spricht von einer vorliegenden
Varianzhomogenität.
Beispiel:
Bei der Feinheitsbestimmung an zwei gleichen Ringspinnmaschinen hatten Stichproben
ergeben:
x1 = 20,1 s1 = 0,176 bei n1 = 10 und x2 = 20,1 s2 = 1,193 bei n2 = 10. Wir prüfen, ob die
Nullhypothese σ1 ≤ σ2 mit einem einseitigen F-Test zur Irrtumswahrscheinlichkeit α = 1% :
s22 1,422
Wegen 2 =
= 45,71 ≥ 3,179 = f9;9;0,99 muss die Nullhypothese verworfen werden und
s1 0,031
davon ausgegangen werden, dass die Varianz der zweiten Produktion signifikant größer ist.:
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
Stand: 17.02.2003
Seite 5 / 8
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
Die Varianzhomogenität beeinflusst den Vergleich von zwei Mittelwerten. Liegt eine
Varianzhomogenität vor, so testet man die Nullhypothese: Die Erwartungswerte sind gleich:
µ1 = µ2 , durch einen T-Test, d.h. man vergleicht die Prüfgröße
x1 − x2
n1n2
n1 +n2
(n1 + n2 − 2)
(n1 − 1)s12 + (n 2 − 1)s22
mit dem Quantil t n1+ n2 −2;1−α / 2 . Ist sie größer als das Quantil, so wird die Nullhypothese
verworfen.
Liegt keine Varianzhomogenität vor, verwendet man die Prüfgröße
x1 − x 2
s12 s22
+
n1 n2
, die man mit
dem Quantil t m;1− α / 2 , wobei m die größte ganze Zahl ist, die kleiner oder gleich
(
s12
n1
( )
s21
1
n1 − 1 n1
2
2
+ ns22
+
)
2
1
n2 −1
( )
s 22
n2
2
ist. (Asymptotischer t-Test).
Beispiel:
Es werden die Garndrehungen von Rotorgarn (20 tex) überprüft, produziert auf 2
Rotorspinnmaschinen gleichen Typs und Einstellungen. Es soll herausgefunden werden, ob
die Abweichungen zufällig sind oder ob sie so beschaffen sind, dass die Maschinen
nachgestellt werden müssen.
Stichprobe
Maschine 1 T/m
Maschine 2 T/m
1
2
3
4
5
901
905
891
889
899
888
881
879
890
879
897
6,78
883
5,22
Mittelwerte:
Standardabweichungen:
F-Test auf Varianzhomogenität (α = 5%) :
s22 6,782
=
= 1,687 ≤ 6,388 = f4;4;0,95 , also gehen
s12 5,222
wir von gleichen Varianzen aus.
T-Test auf gleiche Erwartungswerte (α = 5%):
x1 − x2
n1n2
n1 +n2
(n1 + n2 − 2)
(n1 − 1)s21 + (n 2− 1)s22
man muss demnach von unterschiedlichen Erwartungswerten ausgehen.
= 3,66 > 2,31 = t8;0,975 ,
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
Stand: 17.02.2003
Seite 6 / 8
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
4.
Anpassungstests:
Die bisher beschrieben Tests gehen implizit davon aus, dass die untersuchten Merkmale
normalverteilt sind. Dies muss insbesondere für kleine Stichproben (Umfang geringer als 50)
aber zunächst einmal durch einen sogenannten Anpassungstest statistisch gesichert
werden. Wir beschreiben hierzu einen Schnelltest von David, weiter Tests findet man in der
Literatur im Anhang.
Der Schelltest von David geht vom Verhältnis der Spannweite R zur Standardabweichung s
aus. Eine Normalverteilung ist statistisch gesichert, wenn der Quotient R/s innerhalb
bestimmter Grenzen liegt, hier einige Beispiel für Irrtumswahrscheinlichkeiten von 1% bzw.
5%.
Stichprobenumfang
Untere Schranke
Obere Schranke
q Signifikanzniveau α q
0,005
0,025
0,025
0,005
5
1,98
2,09
2,78
2,81
7
2,22
2,33
3,28
3,37
10
2,46
2,59
3,78
3,94
20
2,94
3,09
4,63
4,91
100
4,03
4,21
6,11
7,60
Beispiel.:
Für die weiter oben bereist behandelte Drehungsprüfung soll die Normalverteiltheit getestet
werden:
Probe Nr.
Drehungen
pro 500mm
x = 1105,2
Die Prüfgröße
1
2
3
4
1090 1110 1125 1050
s = 30.95
5
6
7
8
1057 1110 1141 1136
α = 5%
9
10
1123 1110
R = 1141 – 1050 = 91
R
91
=
= 2,94 liegt zwischen den Tabellewerten 2,59 und 3,28. Daher
s 30,95
kann die Nullhypothese "Die Grundgesamtheit ist normalverteilt." nicht widerlegt werden.
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
5.
Stand: 17.02.2003
Seite 7 / 8
Ausreißertests:
Bei der Auswertung von Stichproben insbesondere von kleinem Umfang können Einzelwerte,
die von den übrigen Messwerten stark abweichen, das Ergebnis, speziell den ermittelten
Mittelwert und die Streuung, verfälschen. Daher sind sie vorab zu prüfen. Lassen sich
Messfehler, Rechenfehler, Schreib- und Datenerfassungsfehler nachweisen, sind diese
Fehler zu korrigieren, sofern die richtigen Einzelwerte verfügbar sind, andernfalls sind sie bei
der Auswertung wegzulassen.
Auch stark abweichende Einzelwerte, die beispielsweise durch Verfahrensänderungen oder
Maschinenumstellungen verursacht sind, werden bei der statistischen Auswertung nicht
berücksichtigt. Allerdings sind in einem Prüfprotokoll die weggelassenen Einzelwerte und der
Grund für die Nichtberücksichtigung festzuhalten.
Kann das starke Abweichen von Einzelwerten nicht wie zuvor beschrieben begründet
werden, so wendet man Ausreißertest an, wenn man mit Hilfe eines solchen Tests
entscheiden will, ob ein abweichender Einzelwert noch der Gesamtheit angehören kann, aus
der die anderen Einzelwerte stammen.
Weist der Test nach, dass Abweichung nicht zufällig war, so bezeichnet man den Wert als
Ausreißer und lässt ihn in der weiteren Auswertung weg. Im Prüfprotokoll ist dann
anzugeben, dass dieser Einzelwert durch einen Ausreißertest eliminiert wurde. Die
wiederholte Anwendung eines Ausreißertests auf die verbleibenden Einzelwerte ist nicht
zulässig. Weist z.B. ein Punktdiagramm darauf hin, dass mehrere Einzelwerte
"ausreißverdächtig" sind, ist ein Test zur gleichzeitigen Elimination mehrerer Ausreißer
anzuwenden.
Verbietet es sich grundsätzlich bei einem Prüfverfahren Einzelwerte wegzulassen, so kann
man als alternatives Lagemaß den ausreißerunabhängigen Median verwenden.
Bei normalverteilten Einzelwerten ist für Stichprobenumfänge n < 30 der Ausreißertest nach
Dixon ein geeigneter Test. Dieser prüft, ob der größte (bzw. der kleinste) Einzelwert einer
Stichprobe als Ausreißer angesehen werden kann. Dazu werden die Einzelwerte nach
aufsteigender Größe geordnet und ein Prüfwert nach einer der Formeln in der folgenden
Tabelle errechnet.
Übersteigt bei gewähltem Signifikanzniveau α der berechnete Prüfwert den Tabellenwert, so
kann der entsprechende Stichprobenwert als Ausreißer angesehen werden.
Das virtuelle Bildungsnetzwerk für Textilberufe
Statistische Analyse von
Messergebnissen
Stand: 17.02.2003
Seite 8 / 8
© 2003 Hochschule Niederrhein
Autor: Prof. Dr. Rudi Voller
Beispiel:
Chromgehalt eines chromschwarz gefärbten Wollgarns
Der Chromgehalt eines chromschwarz gefärbtem Wollgarns wurde viermal bestimmt:
0,53% 0,59% 0,41% 0,58%
Der kleinste Wert x (1) = 0,41% wird als ausreißerverdächtig angesehen. Da keine Erklärung
für diesen niedrigen Wert vorliegt, wird der Dixon-Test auf dem Signifikanzniveau α = 0,05
angewandt. Gemäß der Tabelle ist für n = 4 mit x (1) als ausreißerverdächtigem Einzelwert
der Prüfwert für Ausreißer nach unten
x(2) − x (1)
x (n) − x(1)
=
0,53 − 0,41
= 0,667
0,59 − 0,41
kleiner als der Tabellenwert 0,765. Der ausreißerverdächtige kleinste Wert x (1) = 0,41 darf
also nicht als Ausreißer angesehen und fortgelassen werden.