Die schiefe Ebene

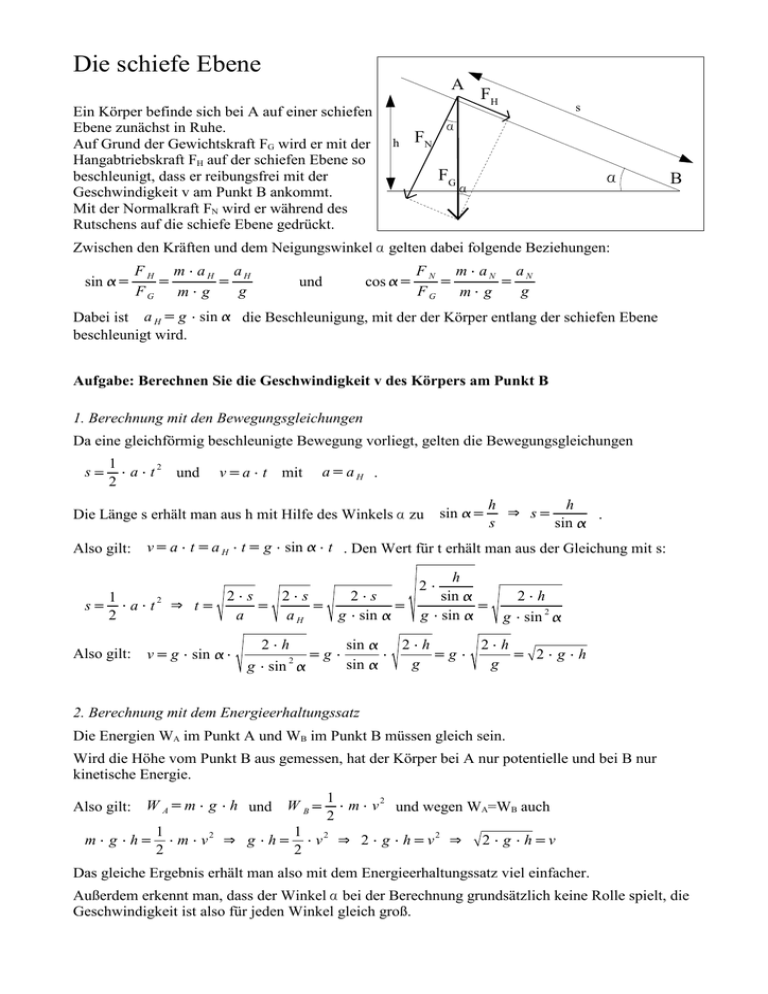
Die schiefe Ebene
A
Ein Körper befinde sich bei A auf einer schiefen
Ebene zunächst in Ruhe.
Auf Grund der Gewichtskraft FG wird er mit der
Hangabtriebskraft FH auf der schiefen Ebene so
beschleunigt, dass er reibungsfrei mit der
Geschwindigkeit v am Punkt B ankommt.
Mit der Normalkraft FN wird er während des
Rutschens auf die schiefe Ebene gedrückt.
h
FH
FG
m aH
m g
aH
g
Dabei ist a H g sin
beschleunigt wird.
FN
B
gelten dabei folgende Beziehungen:
cos und
s
FG
Zwischen den Kräften und dem Neigungswinkel
sin FH
m aN
m g
FN
FG
aN
g
die Beschleunigung, mit der der Körper entlang der schiefen Ebene
Aufgabe: Berechnen Sie die Geschwindigkeit v des Körpers am Punkt B
1. Berechnung mit den Bewegungsgleichungen
Da eine gleichförmig beschleunigte Bewegung vorliegt, gelten die Bewegungsgleichungen
s
1 2
a t und
2
a aH .
v a t mit
Die Länge s erhält man aus h mit Hilfe des Winkels
Also gilt:
s
v a t a H t g sin
1
a t2
2
Also gilt:
2 s
a
t
v g sin h
s
s
h
sin .
t . Den Wert für t erhält man aus der Gleichung mit s:
2 s
aH
2 h
g sin 2 sin zu
2 s
g sin g
sin sin h
sin g sin 2
2 h
g
g
2 h
g sin 2 2 h
g
2 g h
2. Berechnung mit dem Energieerhaltungssatz
Die Energien WA im Punkt A und WB im Punkt B müssen gleich sein.
Wird die Höhe vom Punkt B aus gemessen, hat der Körper bei A nur potentielle und bei B nur
kinetische Energie.
Also gilt: W A m g h und W B m g h
1
m v2
2
g h
1 m v 2 und wegen WA=WB auch
2
1 2
v
2
2 g h v2
2 g h v
Das gleiche Ergebnis erhält man also mit dem Energieerhaltungssatz viel einfacher.
Außerdem erkennt man, dass der Winkel bei der Berechnung grundsätzlich keine Rolle spielt, die
Geschwindigkeit ist also für jeden Winkel gleich groß.