Ψ2 Ψ2 rr 1s 2s (Elektronendichte)

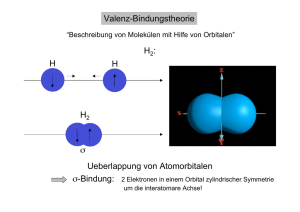
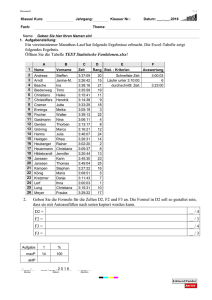
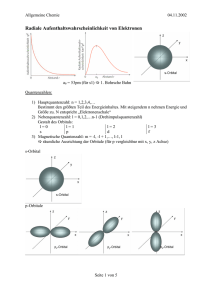
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.
Einführung
1.1
Atomorbitale
Die Atome im Molekülverband werden durch Elektronen verknüpft. Die Elektronen eines
Atoms zeigen Wellennatur. Der für die wellenmechanische Atomtheorie fundamentale mathematische Ausdruck ist die Schrödinger-Gleichung. Sie beschreibt die Beziehung der Wellenfunktion ψ eines Elektrons mit seiner Energie E. Wendet man diese Gleichung auf die Elektronen eines Atoms an, so ist sie nur für diskrete Energieeigenwerte E1, E2, E3, usw. lösbar.
Löst man die Schrödinger-Gleichung für ein Elektron und einen bestimmten Energiezustand
E1, so erhält man eine Wellenfunktion ψ oder einen aus mehreren Gleichungen für ψ bestehenden Satz von Wellenfunktionen. Die Funktion ψ hat ein positives oder negatives Vorzeichen. Eine anschauliche Bedeutung für die Funktion ψ selbst gibt es nicht. Das Quadrat von
ψ2 ist jedoch für einen bestimmten Energiezustand ein Maß für die Aufenthaltswahrscheinlichkeit eines Elektrons im Molekül.
Für ein Atom und eines seiner Elektronen begrenzt ψ2 einen bestimmten Raum um den
Atomkern, in welchen man das Elektron mit größter Wahrscheinlichkeit findet. Diese durch
ψ2 beschriebene Ladungsdichteverteilung eines Elektrons um den Kern wird als Atomorbital
oder Elektronenwolke bezeichnet. Wo die Elektronenwolke am dichtesten ist, hält sich das
Elektron am wahrscheinlichsten auf.
1.1.1
s-Orbitale
Ein s-Orbitale ist kugelsymmetrisch.
2
Ψ (Elektronendichte)
1s
y
Vorzeichen:
überall +
r
x
Ψ
2
2s
Vorzeichen:
überall +
z
r
1
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.1.2
p-Orbitale
Die p-Orbitale sind rotationssymmetrisch be-
y
züglich einer y- bzw. z-Koordinate. Es gibt drei
p-Orbitale: px, py und pz mit hantelförmigem
Umriss. Die ψ-Funktionen der p-Orbitale haben
je einen positiven und negativen Bereich, was
_
+
px-Orbital
x für die LCAO (siehe 1.2.1.1) von Bedeutung ist.
In den Orbitalen, d. h. der graphischen Dar-
stellung von ψ2, wird das Vorzeichen der Wellenfunktion ψ angegeben. Die Größe ψ2 selbst
z
1.1.3
hat naturgemäß nur ein positives Vorzeichen.
Elektronenkonfiguration leichter Elemente
Energiezustände E1 und E2: 1s, 2s, und 2p-Orbitale.
E
2px
2py
2pz
2s
1s
Regeln zur Besetzungsreihenfolge:
1) Energie:
Zuerst werden die energieärmsten Orbitale besetzt.
2) Pauli-Prinzip: Bis zu zwei Elektronen können ein Orbital besetzen. Im Falle einer
Doppelbesetzung müssen die Elektronenspins antiparallel ein.
3) Hund-Regel:
Ist ein Satz entarteter (d. h. energiegleicher) Orbitale verfügbar, z. B. 2px,
2py, 2pz, so werden alle Orbitale erst einzeln belegt, bevor eines doppelt
besetzt wird.
2
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.2
Atom
1s
2s
2px 2py 2pz
Symbol
H
↑
1s
He
↑↓
1s2 ≡ <He>
Li
↑↓
↑
<He> 2s
Be
↑↓
↑↓
<He> 2s2
B
↑↓
↑↓
↑
C
↑↓
↑↓
↑
↑
N
↑↓
↑↓
↑
↑
↑
<He> 2s2 2p3
O
↑↓
↑↓
↑↓
↑
↑
<He> 2s2 2p4
F
↑↓
↑↓
↑↓
↑↓
↑
<He> 2s2 2p5
Ne
↑↓
↑↓
↑↓
↑↓
↑↓
<He> 2s2 2p6
<He> 2s2 2p
<He> 2s2 2p2
Kovalente Bindung
Durch Überlappung von Atomorbitalen entstehen kovalente Bindungen zwischen Atomen
(Elektronenpaarbindung). Die Metall- und die ionische Bindung sind für die organische
Chemie ohne Bedeutung.
1.2.1
σ -Bindungen
1.2.1.1 Wasserstoff (H2)
•
Valence Bond (VB) Theorie: In den Molekülen vermitteln Elektronenpaare zwischen
den Atomkernen die chemische Bindung; Symbolik: Ein Punkt ist ein ungepaartes
Elektron, ein Strich ein Elektronenpaar.
H·
1s1
+
·H
H H
1s1
σ2
3
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
•
Molekülorbital (MO) Theorie: Durch Linearkombination von Atomorbitalen ψ1 und
ψ2 (LCAO), d. h. Addition oder Subtraktion der Wellenfunktionen, entstehen neue
Molekülorbitale σ und σ*. Diese werden entprechend den in Abschnitt 1.1.3
erläuterten Regeln besetzt:
σ* = ψ1 – ψ2;
σ = ψ1 + ψ2
E
σ∗
+
1s
Energiegewinn (2 x)
σ
1s
bindendes Molekülorbital
σ-MO (σs,s-MO)
antibindendes Molekülorbital
σ∗-MO
_
+
Vorzeichen: überall +
Nullstelle
Der Energiegewinn ergibt sich aus der Bruttoenergieabsenkung aller beteiligten Elektronen.
1.2.1.2 Fluor (F2)
F·
·F
+
+
px
_
+
px
F
2
σp,p
2p1
2p1
_
F
_
+
_
σp,p-MO
4
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.2.1.3 Fluorwasserstoff (HF)
F·
+
2p1
_
·H
F H
1s1
2 -MO
σp,s
_
+
+
+
1.2.2
π -Bindung: Sauerstoff (O2)
σ-Bindungen sind rotationssymmetrisch bezüglich der Kernverbindungsachse ("Einfachbindungen"). Eine π-Bindung ist nicht rotationssymmetrisch und besitzt entlang der Kernverbindungsachse eine Knotenebene ("Nullstelle"). Eine Doppelbindung besteht aus einer σ- und
einer π-Bindung.
O·
·O
·
+
·
O O
eine σ- und
eine π-Bindung
σ-Bindung:
_
+
_
+
_
+
px
σp,p-MO
+
+
+
_
_
_
pz
pz
πp,p-MO
px
_
π-Bindung:
Ψ2 = 0 entlang der
Kernverbindungsachse
Achtung: Aus didaktischen Gründen ist dies ein stark vereinfachtes Bild von O2. Es handelt sich eigentlich um ein Diradikal.
5
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.2.3
Hybridisierung
1.2.3.1 Methan (CH4)
sp3-Hybridisierung:
C·
2 ·H
+
·
H
?
keine stabile Verbindung!
C
H
2x σs,p-MO
Experiment: CH4 ist stabil
H
H
vier gleiche Bindungen in den Ecken eines Tetraeders
C
(Winkel: 109°28' ≈ 109.5°)
H
H
Lösung: neue Theorie → Hybridisierung
C:
2s2
2p2
vier gleiche Orbitale ≡
4 sp3-Hybridorbitale
Mathematik: 1 sp3 ≡ 25% s + 75% p
Energie:
E
px
py
pz
∑=0
4 x sp3
s
Methan: 4 x σs,sp3 -MO
_
_
+
C: sp3
H: s
+
σsp3 ,s -MO
Die vier sp3-Hybridorbitale sind entartet und in die Ecken eines Tetraeders gerichtet.
6
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
Auch andere Formen von Hybridisierung sind denkbar:
sp2-Hybridorbital: sp2 ≡ 1/3 s + 2/3 p
Energie:
E
py
px
pz
∑=0
pz
3 x sp2
s
Geometrie: trigonal planar, Winkel: 120°
+
_
+
in xy-Ebene
(z-Achse: pz-Atomorbital)
_
_
+
sp-Hybridorbital: sp ≡ 50% s + 50% p
Energie:
E
px
py
∑=0
pz
2 x sp
s
py
pz
Geometrie: linear, Winkel: 180°
+
_
_
+
x
2 sp-Orbitale entlang der x-Achse
(y,z-Achsen: py, pz-Atomorbitale)
7
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.2.3.2 Ethan (C2H6): C–C-Einfachbindung
H
H
·
·
·C· ·H
·
·
·
·
H· ·C·
·
·
H
H
1s1
H
H
H
+
H
C
C
H
H
σsp 3, s
4 x sp3
H
_ C
H
C _
H
σsp 3, sp3
Winkel: 109°28'
H
H
H
σsp 3, sp3 -MO
C-C-Einfachbindung
zwei eckenverknüpfte Tetraeder
1.2.3.3 Ethen (C2H4): C–C-Doppelbindung
H
H
C
planar, Winkel H,C,H ≈ 120°
C
sp2-Hybridisierung am C: 3 sp2 + 1 pz Orbital
H
H
H
+
+
H
C
_
C
_
H
+
H
C
H
σs, sp2
H
σsp2 , sp 2
_
H
C
H
π p, p-MO
pz
C=C besteht aus:
1 σsp 2, sp 2 -MO
1 π p, p-MO
kantenverknüpfte Tetraeder
Der C–C-Abstand beträgt im Ethen 134 pm und im Ethan 154 pm. Ein σ(sp2,sp2)-MO besitzt
also mehr s-Charakter als ein σ(sp3,sp3)-Molekülorbital.
8
Prof. Christoffers, Vorlesung Organische Chemie für Verfahrensingenieure, Umweltschutztechniker und Werkstoffwissenschaftler
1.2.3.4 Ethin (C2H2): C–C-Dreifachbindung
H
H
C
linear, Winkel: 180°, Abstand C-C: 120 pm
H
C
+
σs,sp
σsp,sp
z
+
sp-Hybridisierung am C: 2 sp + 1 py + 1 pz Orbital
H
z'
_
+ _
+
_
pz
x
+ _
py
y
y'
H
πp
y, py
+
_
+
_
+ πp
z,p z
H
-MO
Die C–C-Dreifachbindung im Ethin besteht aus einem bindendem σ(sp,sp)-Molekülorbital
sowie zwei bindenden π(p,p)-Molekülorbitalen. Die beiden π-Orbitale stehen orthogonal zueinander, eines in der x,y-Ebene, das andere in der x,z-Ebene. Die beiden C–H-Einfachbindungen kommen durch bindende σ(sp,s)-Molekülorbitale zustande.
9