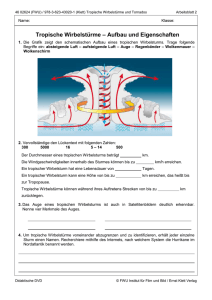
Tropische Wirbelstuerme
Werbung

Die Dynamik tropischer Wirbelstürme Roger K. Smith Universität München Inhalt ¾ Allgemeine, beobachtete Struktur ¾ Dynamische Prozesse Primäre Zirkulation Dynamik des Auges Reibungseinflüsse und sekundäre Zirkulation Intensivierung von Wirbeln Der WISHE Mechanismus ¾ Ein minimales Hurrikanmodell ¾ Offene Fragen und Probleme 1 Hurrikan Mitch, Oktober 1998 Taifune Zyklone Entstehungsgebiete Tropische Zyklone Hurrikane Tropische Zyklogenese benötigt eine Wassertemperatur von über 26.5 Grad C 2 Bahnen tropischer Wirbelstürme (1979-1988) Gemittelte Bahnen tropischer Wirbelstürme 3 Zugbahnen der Hurrikane 1998 4 Hurrikan Forschungsflugzeug NOAA WD-P3 5 Radarbild vom Heckradar Schematischer Querschnitt durch einen Hurrikan Cirrus Cirrus Auge Eyewall Spiralbänder 6 Vertikal-radialer Schnitt durch einen Hurrikan Isothermen Äquivalentpotentielle Temperatur θe warm Houze Fig. 10.11 Flüsse latenter Wärme Isotachen Aus Wallace and Hobbs (1977) Kräftebilanz in einem Wirbel Rotationsachse Primäre (tangentiale) Zirkulation niedrigster Druck im Zentrum Druckgradientkraft r v Zentrifugalkraft und Corioliskraft Gradientwindbalance v2 1 ∂p + fv = r ρ ∂r 7 Primäre (tangentiale) Zirkulation z Gradientwindbalance v2 1 ∂p′ + fv = r ρ ∂r warm kühl v(r,z) Hydrostatisches Gleichgewicht 8 0=− 1 ∂p′ + σ, ρ ∂z σ= g(T − To ) To r Thermischer Wind ⇒ 2v ∂v g ∂T +f = +… r ∂z To ∂r Grossaufnahme des Auges 8 Dynamik des Auges z Gradientwindbalance v2 1 ∂p′ + fv = r ρ ∂r warm 0=− 1 ∂p′ +σ ρ ∂z − v(r,z) 8 ∂ p′(z,0) = ∂z p′(z, ∞) − p′(z,0) = ∫ ∞ 0 ∫ ∞ 0 kühl v2 ρ + fv dr r r ∂ v ρ + fv dr < 0 ∂z r 2 ∂v <0 ∂z Reibungsbedingte sekundäre Zirkulation sekundäre Zirkulation Druckgradient -kraft r v v Zentrifugalkraft und Corioliskraft werden durch Reibung verringert 9 Dynamik des Spinups von Wirbeln ¾ Basisprinzip: - Erhaltung des absoluten Drehimpulses: M = rv + r2f/2 r v v = M/r − rf/2 Wenn r abnimmt, nimmt v zu! Spinup benötigt radiale Konvergenz Dynamik des Spindowns von Wirbeln Vertikaler Schnitt ∂V ∂t V ∂w <0 ∂z 8 ∂w >0 ∂z Grenzschicht Divergenzfreie Höhe 10 Auftrieb in einem Wirbel ⇒ Auftrieb warm ∂w <0 ∂z Tv Tv ∂w >0 ∂z 8 Reibungsschicht Divergenzfreie Höhe Auftriebskraft ∝ horizontaler (virtueller) Temperaturunterschied Theorie des “Wind-induced Surface Heat Exchange” (WISHE) M = rv + 12 r 2f warm Auge M, θe = const Tv (r, p) ∝ θ*e (r, p) θe1 θe2 v θeb1θeb2 8 Antizyklonisch Erhöhung vom V => Druckabnahme: Beides => Erhöhung des Flusses latenter Wärme => Verstärkung des radialen θe Gradienten => Erhöhung der Konvergenz => Zunahme von V … u.s.w. ABER kein unbegrenzter Prozess! 8 Flüsse latenter Wärme ∝ Cq|Vs|(q*(Ts,p) – qb) Ts 8 q* ∼ r* = εe * (T) p − e * (T) 11 Die Parameterisierung hochreichender Konvektion Mc2 Mc2 Mc2 – Μ2 Me Abwind Md4 Mc4 Schicht-1 Mc4 Schicht -3 Mc4 – Md4 – Μ4 Schicht -b Gitterbox Mc4 durch Schliessungsansatz 12 Maximale tangentiale Windgeschwindigkeit in der mittleren Schicht Vmax (ms−1) 4 = Ooyama 2 = Arakawa 3 = Emanuel 1 = Explizit Zeit (Std) Einige offene Fragen und Probleme ¾ Wie verhalten sich komplexe Modelle? ¾ Asymmetrische Spinup-Mechanismen ¾ Wechselwirkung mit Trögen in der oberen Atmosphäre ¾ Scherung des Horizontalwindes mit der Höhe ¾ Einfluss des Bodens: z.B. Ozeanoberfläche, das Verhalten des Austauschkoeffizienten in Bodennähe bei starkem Wind (> 20 m/s) ¾ Starkniederschläge ¾ Initialisierung von Vorhersagemodellen ¾ Umwandlung tropischer Zyklone im extratropische Systeme 13