4.9.7 Konstruktion der Suffixbäume

4.9.7
Konstruktion der Suffixbäume
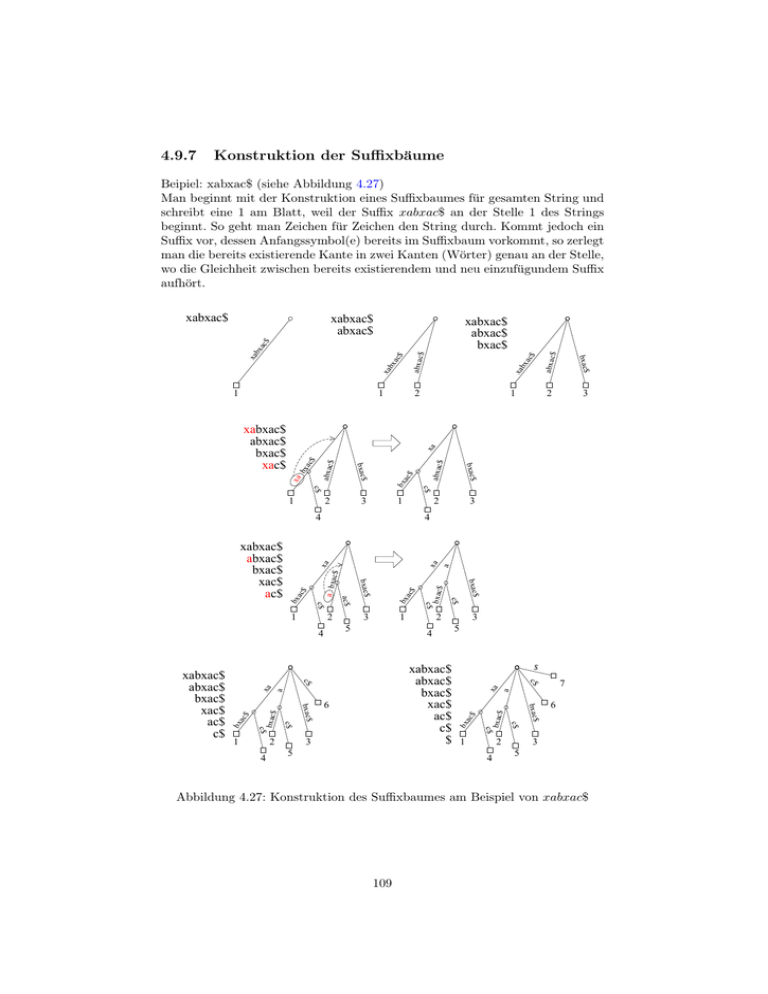
Beipiel: xabxac$ (siehe Abbildung 4.27)
Man beginnt mit der Konstruktion eines Suffixbaumes für gesamten String und
schreibt eine 1 am Blatt, weil der Suffix xabxac$ an der Stelle 1 des Strings
beginnt. So geht man Zeichen für Zeichen den String durch. Kommt jedoch ein
Suffix vor, dessen Anfangssymbol(e) bereits im Suffixbaum vorkommt, so zerlegt
man die bereits existierende Kante in zwei Kanten (Wörter) genau an der Stelle,
wo die Gleichheit zwischen bereits existierendem und neu einzufügundem Suffix
aufhört.
xabxac$
abxac$
1
$
abxac
$
bx
ac
$
$
7
xa
a
$
bx
ac
1
2
4
6
c$
3
5
bxac$
bx
ac
$
a
xa
xa
a bx
ac$
bxac$
$
abxac
bx
ac
xa
bx
ac
$
xa
a
6
$
b x ac$
xabxac$
abxac$
bxac$
xac$
ac$
c$
$
3
5
c$
bxac$
2
4
c$
$
c$
1
c$
bx
ac
3
bxac$
b x ac$
4
bxac$
3
5
c$
c$
2
3
c$
ac$
bxac$
2
4
1
2
4
c$
1
2
1
4
xabxac$
abxac$
bxac$
xac$
ac$
c$
1
c$
bxac$
3
c$
2
1
xabxac$
abxac$
bxac$
xac$
ac$
xa
bx
ac
2
xa
xabxac$
abxac$
bxac$
xac$
$
$
ab x ac
$
xa
bx
ac
1
bxac$
xa
bx
ac
$
xabxac$
abxac$
bxac$
ab x ac
xabxac$
3
5
Abbildung 4.27: Konstruktion des Suffixbaumes am Beispiel von xabxac$
109
Naiver Algorithmus zu Konstruktion von Suffixbäumen. Konstruiere
Folge T1 , T2 ,..., Tn von Bäumen, wobei Ti alle Suffizies S[1..n], S[2..n],..., S[i..n]
enthält. D.h., der Baum T1 hat nur eine Kante und enthält nur einen Suffix
S[1..n] = S (Abbildung 4.28), T2 enthält Suffizies S[1..n], S[2..n] usw.
T1 :
1
Abbildung 4.28: Erster Schritt bei der Aufbau eines zunächst leeren Suffixbaumes
Ti+1 wird aus Ti wie folgt konstruiert:
1: Durchlaufe Ti mit dem Suffix Si+1 (= S[i + 1..n]) wie beim Matching
Algorithmus bis man "stecken bleibt".
Also (Abbildung 4.29): Si+1 = αβ, wobei α ist ein maximaler Präfix,
der als Markierung eines Knotens u (d.h. Beschriftung des Weges
von Wurzel bis u) plus Präfix α0 , der Markirung γ einer von u
ausgehender Kante e = (u, v) auftritt.
2: Wir schaffen ein neues Blatt w mit dem Index i + 1
3: Falls α0 = ε (leeres Wort) (Abbildung 4.30):
schaffe eine neue Kante e0 = (u, v) und beschrifte sie mit β
Sonst (Abbildung 4.31): sei γ = α0 β, wobei α0 6= ε, δ 6= ε
schaffe neuen Knoten x
spalte Kante e in e1 = (u, x) und e2 = (x, v)
schaffe neue Kante e0 = (x, w)
beschrifte e1 mit α0 , e2 mit δ, e0 mit β
Wurzel
α
α' γ
u
α'
γ
v
Abbildung 4.29: α0 ist Präfix eines existierenden Suffixes im Baum
110
Wurzel
α
α'=ε (leeres Wort)
u
γ
β
w
v
i+1
Abbildung 4.30: α0 = ε (Leeres Wort)
Wurzel
α
γ=α'δ, α'≠ε, δ≠ε
u
γ
β
w
i+1
α'
δ
x
v
Abbildung 4.31: γ = α0 δ, wobei α0 6= ε, δ 6= ε
111
Laufzeit
Für jeden Suffix Si (|Si | = n−i+1) wird eine Suche durchgeführt, die O(n−i+1)Zeit kostet. Schritte 2 und 3 benötigen
konstante Zeit, also O(1).
!
n
X
Insgesamt : O
n − i + 1 = O n2
i=1
{z
|
Pn
j=1
j=
}
2
n(n+1)
≈ n2
2
Speicherbedarf
Die Größe des entstehenden Baumes (Speicherbedarf), einschließlich der Beschriftungen der Kanten ist O(n2 ).
Best case ist nur dann zu erwarten wenn alle Zeichen gleich sind (S = an ),
so liegt der Speicherbedarf bei O(n) und der Baum sieht wie auf der Abbildung 4.32 aus:
Abbildung 4.32: Suffixbaum mit dem Speicherbedarf O(n)
Sonst aber kommt es an Θ(n2 ) heran, was für große Texte (Buch, DNA-Analyze)
nicht akzeptabel ist.
In der Praxis wird eine andere Konstruktion/Modifikation des Suffixbaumes verwendet, die in linearer Zeit konstruiert werden kann und linearer Speicherplatz
benötigt. Dabei handelt es sich um das Algortihmus von Ukkonen (AU). Wir
werden den Algorithmus nicht näher betrachten, da er sehr kompliziert ist.
4.9.8
Anwendungen von Suffixbäumen
1 Stringmatching
Konstuktion des Suffixbaumes mit AU mit anschließender Suche nach P
liefert alternativen O(n + m)-Algorithmus.
1a Finden einer Menge von Strings {P1 , .., Pl } in einem Text S
Zu finden sind alle Vorkommen von Mustern im Text S.
Das ist machbar in Vorverarbeitungszeit O(n) mit AU. Laufzeit für eigentPk
liche Suche beträgt O(m + k), wobei m = i=1 |Pi |, k ist Anzahl aller
Vorkommen.
2 Datenbank von Texten S1 , ..., Sl
Zu finden sind alle Vorkommen eines Musters P in Texten S1 , ..., Sl .
112
Dafür werden die Texte zusammengestellt getrennt durch spezielle Trennzeichen $i die weder im Text noch im Muster vorkommen: S1 $1 S2 $2 ..$l−1 Sl .
Ohne dieser Trennzeichen wäre es möglich ein Muster so zu finden, dass
sein Präfix in Sj und sein Suffix in Sj+1 liegt.
Dafür bauen wir einen Suffixbaum auf. Vorverarbeitungszeit beträgt O(n),
Pl
n = i=1 |Sl |, Suchzeit ist O(m + k), wobei m = |P | und k ist Anzahl
aller Vorkommen.
3 Suche nach dem längsten gemeinsamen Teilwort
Gegeben sind Strings S1 und S2 .
Zu finden ist das längste gemeinsame Teilwort.
Idee:
- konstruiere einen Suffixbaum wie in o.a. Anwendung 2. für S1 und S2
- markiere jeden inneren Knoten v mit 1, falls sein Unterbaum einen Suffix
von S1 enthält und mit 2 falls einen Suffix von S2 . D. h. in v endet sich
ein Teilwort von S1 (oder S2 )
- finde tiefsten Knoten, der mit 1 und 2 markiert ist, wobei die Tiefe =
Länge der Beschriftungen von der Wurzel bis dorthin. Mit AU lässt sich
das Problem in O (|S1 | + |S2 |) Zeit lösen.
Ungestritten gibt es viele weitere Anwendungen. Einige der wichtigen davon
finden sich in der Bioinformatik.
4.9.9
Anwendungen in der Bioinformatik
Definition 4.9.2 (DNA-Moleküle (deutsch: DNS - Desoxyribonukleinsäure)).
Moleküle, die die Erbinformation eines Organismus enthalten und sind Doppelketten aus folgenden Bausteinen (Molekülen) {A, T, C, G} (Adenin, Thymin,
Cytosin, Guanim). Einzelne Bausteine heißen Nukleotide. Ein Molekül besteht
aus ≈ 109 − 1010 Nukleotiden.
Dabei gibt es zwei Zuordnungen: A ↔ T und C ↔ G.
Definition 4.9.3 (Genom). Gesamtkette der DNA-Moleküle, die gesamte Erbinformation enthält (mehr dazu kann man z.B. bei http://de.wikipedia.
org/wiki/Genom nachlesen).
Definition 4.9.4 (Protein). Ein String über einem 20-elementigen Alphabet
(die Zeichen des Alphabets sind die Aminosäuren). Die Länge eines solchen
Strings kann mehrere Hunderte sein. (z.B.: bei Bakterien: 500-1500, bei Menschen (Säugetieren) ≈ 100.000).
Definition 4.9.5 (Genetischer Code). Codierung eines Aminosäurenbausteins
im Protein durch jeweils ein Tripel von aufeinanderfolgenden Nukleotiden.
Beispiel (Genetischer Code). TTT - Phenylamin, GTT - Valin
Da es um die Tripeln handelt, ist es wichtig bei der Decodierung eines DNAAbschnittes an der richtigen Stelle anzufangen (man weiß nicht genau, am Anfang des DNA-Stücks der Tripel ’sauber’ oder innendrin getrennt wurde).
Definition 4.9.6 (Sequenzierung). Bestimmung der Folge von Nukleotiden eines DNA-Moleküls.
113
Den ganzen Genom erhält man durch das Überlappen einzelner Stücke (Abbildung 4.33). Bisher (Stand: 2004) ist es technisch möglich Stücke der Länge
300-500 zu identifizieren. Dabei soll man bedenken in welche Richtung die Einzelstücke bei dem Überlappen gerichtet werden sollen.
Abbildung 4.33: Rekonstruktion eines Genoms durch das Überlappen der DNAFragmente
Es gibt also folgendes Problem (theoretisch) zu lösen: gegeben sind viele Teilworte, gesucht ist das kleinste gemeinsame Oberwort.
Dieses Problem ist NP-schwer und ist ein gutes Beipiel für die o.a. Anwendung
1.a (Finden einer Menge von Mustern in einem Text) 4.9.8. Dabei ist der Text
ein bereits sequinziertes DNA-Stück. Jedes neue Fragment wird gegen den Text
getestet, ob nicht bereits vorhanden. Ist es nicht der Fall, so sucht man nach
einer Überlappung mit dem Ende des Textes.
114