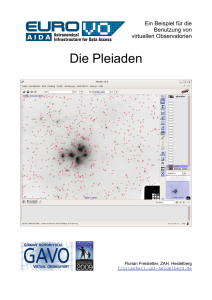
Astrophysikalisches Praktikum fuer Fortgeschrittene: Photometrie

Fortgeschrittenen-Praktikum
Versuch Photometrie und
Spektroskopie
Cornelia Heinitz
Kepler Center for Astro and Particle Physics
Institut für Astronomie und Astrophysik
Sand 1
72076 Tübingen
Stand: 14. Juli 2016
http://www.uni-tuebingen.de/de/4203
Inhaltsverzeichnis
1
Vorbemerkung
3
2
Einführung
2.1 Koordinatensysteme . . . . . . . . . . . . . . . . . . . .
2.2 Teleskope . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.1 Öffnungsverhältnis . . . . . . . . . . . . . . . .
2.2.2 Das Auflösungsvermögen . . . . . . . . . . . .
2.2.3 Refraktoren . . . . . . . . . . . . . . . . . . . .
2.2.4 Reflektoren . . . . . . . . . . . . . . . . . . . .
2.2.5 Teleskopmontierungen . . . . . . . . . . . . . .
2.2.6 Aktive und adaptive Optiken . . . . . . . . . . .
2.3 Bilddetektoren . . . . . . . . . . . . . . . . . . . . . . .
2.3.1 Grundlagen des CCD . . . . . . . . . . . . . . .
2.3.2 CCDs in der Astronomie . . . . . . . . . . . . .
2.4 Spektroskopie . . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Beugungstheorie am Gitter . . . . . . . . . . . .
2.4.2 Die Dispersion . . . . . . . . . . . . . . . . . .
2.4.3 Das Auflösungsvermögen . . . . . . . . . . . .
2.5 Strahlungstheorie . . . . . . . . . . . . . . . . . . . . .
2.6 Strahlungsintensität und Strahlungsfluss . . . . . . . . .
2.6.1 Strahlung im thermodynamischen Gleichgewicht
2.6.2 Effektivtemperatur und Leuchtkraft . . . . . . .
2.6.3 Helligkeiten und Farben . . . . . . . . . . . . .
2.7 Farben-Helligkeits-Diagramm . . . . . . . . . . . . . .
2.8 Spektralklassen . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
4
6
6
7
9
10
13
16
19
19
22
23
24
26
27
27
27
28
29
30
30
31
3
Versuchsaufbau
3.1 Spiegelteleskop . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Der 10 C-Gitterspektrograph . . . . . . . . . . . . . . . . . . . . . . .
3.3 CCD-Kameras STL-1001E und HX916 . . . . . . . . . . . . . . . . .
34
34
35
38
4
Versuchsdurchführung
4.1 Vorbereitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Sternspektroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Photometrie eines Sternhaufens . . . . . . . . . . . . . . . . . . . . . .
39
39
40
46
5
Literatur
49
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A Mögliche Beobachtungsobjekte
50
B Wellenlängenkalibration
51
C Starke Linien in Sternspektren.
52
D Aufbau des Versuchsprotokolls
56
2
1
Vorbemerkung
Der Versuch “Photometrie und Spektroskopie” soll grundlegende Methoden zur Aufnahme und Auswertung astronomischer Daten verständlich machen. Dabei soll insbesondere auf die auch sonst in der Physik anwendbaren technologischen Grundlagen
eingegangen werden. Neben einem Verständnis für die Funktionsweise der Instrumente sind die praktische Anwendung, die wissenschaftliche Motivation und die zugrunde
liegende Physik der Anwendungsbeispiele das Entscheidende.
Astronomische Kenntnisse auf dem Niveau der Einführungsvorlesung sind für die
Durchführung des Versuchs zwinged erforderlich, Erfahrung im Umgang mit Computern ist vorteilhaft, aber keineswegs notwendig. Wir haben versucht, in dieser Anleitung die für die Durchführung des Versuchs notwendigen Informationen zusammenzustellen. Darüber hinausgehende Informationen finden Sie in der zitierten Literatur.
Die Programmbefehle zur Steuerung der Kamera und der verwendeten Software sind
alle aufgeführt, es wird aber nicht erwartet, dass Sie damit ohne weitere Einweisung
vor Ort zurechtkommen. In der Astronomie ist es immer noch gebräuchlich, Einheiten,
die nicht dem SI-System entstammen, zu verwenden. Prominente Beispiele sind das
Ångström als Wellenlängeneinheit oder der Tag als Zeiteinheit. Diese Anleitung folgt
dieser Gepflogenheit, lassen Sie sich bitte nicht von etwas ungewohnten Einheiten abschrecken. . .
Um Ihnen die Vorbereitung des Versuchs zu vereinfachen, haben wir in diese Einleitung einfache Aufgaben eingestreut. Sie sollten diese Aufgaben vor dem Praktikum
gelöst haben, die Lösung ist Teil Ihres Praktikumsprotokolls. Im Ausgleich für diese
Vorarbeit kann die Nachbereitung des Versuches wesentlich kürzer ausfallen.
2
Einführung
Im Gegensatz zu allen anderen Naturwissenschaften ist die Astronomie eine rein empirische Wissenschaft. Es ist den Astronomen unmöglich, die Gegenstände ihrer Untersuchungen unter kontrollierten Bedingungen zu manipulieren oder Experimente mit
ihnen anzustellen. Die alleinige Information, die zur Wissensgewinnung dient, liegt in
der Form der von astrophysikalischen Quellen beobachteten Strahlung vor. Die Kunst
der Astronomie als Wissenschaft liegt darin, die in der Strahlung steckende Information
auszuwerten.
Die von astronomischen Quellen beobachtete Strahlung ist meist sehr schwach,
Strahlungsflüsse von 10−29 W cm−2 s−1 (=1 mJy [milli Jansky], astronomische Einheit
für Strahlungsflüsse) im optischen oder einigen wenigen Photonen pro cm2 und Sekunde im Röntgenbereich sind üblich1 . Zusätzlich ist unser Beobachtungsstandort auf
der Erde ein äußerst ungünstiger – die detektierte Strahlung muss vor der Beobachtung
die Erdatmosphäre passieren, die Erde ist keine ruhende Plattform, sondern dreht sich
usw. . . Der Drang zur Untersuchung immer schwächerer Objekte führte im 20. Jahrhundert zur Entwicklung immer größerer Teleskope und zur Entwicklung sehr lichtempfindlicher Detektoren. In dieser Einführung möchten wir Sie mit den Grundlagen
1 Eine in der Astrophysik der kosmischen Strahlung gebräuchliche Einheit ist die der detektierten Teil-
chen, die pro Quadratkilometer und Jahr gemessen werden – die Detektionsgrenze für den Teilchenfluss
liegt hier im Bereich von ungefähr 10−2 Teilchen km−2 a−1 . . .
3
dieser Detektoren, soweit sie für das Praktikum von Bedeutung sind, vertraut machen.
Wir werden uns dabei zunächst mit astronomischen Teleskopen beschäftigen und dann
auf die Detektoren für elektromagnetische Strahlung eingehen.
2.1
Koordinatensysteme
Das Aufsuchen von astronomischen Objekten erfordert die Festlegung eines Koordinatensystems. Es ist dabei sinnvoll, ein System zu definieren, das vom Beobachtungsort
und der Zeit unabhängig ist. Da wir es in der Astronomie, abgesehen von Objekten innerhalb unseres Sonnensystems, mit sehr großen Entfernungen zu tun haben, können
wir ein Koordinatensystem auf einer unendlich großen Himmelskugel festlegen und so
auf zwei Koordinaten einschränken. Die Änderung der Koordinaten aufgrund der täglichen bzw. jährlichen Erddrehung ist sehr klein, da die Entfernung der Objekte viel
größer als der Erdbahnradius ist (der nächste Stern, Proxima Centauri, hat eine Entfernung von etwa 270000 Erdbahnradien).
Abbildung 1: Himmelskugel mit Himmelskoordinaten (Quelle: Unsöld & Baschek, 1988,
Abb. 2.2.3).
Da die Ausrichtung der Rotationsachse der Erde im Raum (nahezu) fest ist, ist eine Projektion des äquatorialen Systems auf die Himmelskugel ein geeignetes orts- und
zeitunabhängiges Bezugssystem. Die Schnittlinie zwischen der Himmelskugel und der
Äquatorebene ist ein Großkreis, der als Himmelsäquator bezeichnet wird. Die Verlängerung der Erdachse definiert die Himmelspole (siehe Abb. 1). Der Winkelabstand eines
Sterns von der Äquatorebene wird durch die Erdrotation nicht beeinflusst. Dieser Winkel wird auf einem Großkreis, der durch beide Himmelspole und den Stern verläuft, dem
sog. Stundenkreis, abgetragen und als Deklination δ bezeichnet. Gemessen wird von der
Äquatorebene aus, positive Winkel bezeichnen Objekte auf der Nordhalbkugel, negative
solche auf der Südhalbkugel. Dies ist die erste Koordinate. Die zweite Koordinate wird
4
auf dem Äquator gegen den Uhrzeigersinn gemessen. Wir benötigen aber noch einen
Bezugspunkt, der von der Erdrotation unabhängig ist. Die Wahl dieses Punktes ist im
Prinzip beliebig, es macht aber Sinn, einen Punkt mit besonderen Eigenschaften auszuwählen. Die projizierte Bahn der Sonne, die Ekliptik, schneidet den Himmelsäquator an
den Punkten der Tagundnachtgleichen. Einer dieser beiden Schnittpunkte, nämlich der
Frühlingspunkt, wird als Bezugspunkt gewählt. Früher befand sich dieser im Sternbild
Widder und wird daher auch Widderpunkt (ϒ) genannt. Der Winkel zwischen Objekt
und Frühlingspunkt auf dem Äquator wird in Stunden angegeben. Damit haben wir die
zweite Koordinate, die Rektaszension α (oder auch R.A.).
Die Präzession der Erdachse bewirkt eine Änderung der Koordinaten, für eine präzise Katalogisierung benötigen wir also noch die Angabe desjenigen Zeitpunktes, die
sog. Epoche, an dem der Frühlingspunkt definiert wurde, z.B. 1950 oder 2000. Es gibt
noch weitere Effekte, die die Koordinaten beeinflussen, auf die hier aber nicht weiter
eingegangen werden soll.
Aufgabe 1: Verschaffen Sie sich die Koordinaten der Objekte aus der Objektliste
(Tab. 7), z.B. unter Zuhilfenahme der Datenbank SIMBAD (http://simbad.
u-strasbg.fr/Simbad).
5
O du vielwissendes Rohr, kostbarer
als jedes Szepter! Wer dich in seiner
Rechten hält, ist er nicht zum König,
nicht zum Herrn über die Werke
Gottes gesetzt!
Johannes Kepler
Dioptrice, 1611
2.2
Teleskope
Von den in der Einleitung dargestellten Gegebenheiten lassen sich die folgenden Anforderungen an astronomische Teleskope ableiten: Teleskope müssen über
• eine möglichst hohe Lichtausbeute,
• ein gutes Auflösungsvermögen
• und natürlich eine sehr gute Bildqualität
verfügen. Es gibt zwei verschiedene Klassen von Teleskopen, mit denen diese Anforderungen erreicht werden können. Zum einen sind dies die Refraktoren, bei denen mit
Hilfe von Linsensystemen eine Abbildung erreicht wird, zum anderen die Reflektoren,
bei denen das Gleiche mit Hilfe der Kombination von sphärisch oder parabolisch geschliffenen Spiegeln erreicht wird.
2.2.1
Öffnungsverhältnis
Abbildung 2: Herleitung des Abbildungsmaßstabs.
Beiden Arten von Teleskopen ist gemein, dass sie das sich im Unendlichen befindliche
astronomische Objekt mit einem Objektiv oder Hohlspiegel des Durchmessers D und
der Brennweite f in eine Fokalebene projizieren, in der das Bild des Objekts untersucht
wird. Abbildung 2 zeigt als Beispiel den Strahlengang eines einfachen Reflektors. Das
Verhältnis D/ f bezeichnet das Öffnungsverhältnis des optischen Systems, beim Photoapparat ist das Inverse des Öffnungsverhältnisses, f /D, als die Blendenzahl bekannt.
Aus Abbildung 2 kann die Bildausdehnung a eines im Unendlichen unter dem Winkel
ω erscheinenden Objekts abgelesen werden:
a = 0.0175 ω f
(1)
wobei ω im Gradmaß gemessen wird. Ein Teleskop mit einer Auffangfläche ∼ D2 konzentriert also die aufgefangene Energie eines flächenhaften Objekts auf einer Fläche
6
∼ f 2 . Das Verhältnis dieser Größen definiert daher die Lichtstärke:
2
D
Lichtstärke ∝
f
(2)
Die Lichtstärke bei flächenhaften Objekten ist also nur vom Öffnungsverhältnis abhängig (also von der “Blendenzahl”, wie beim Photoapparat). Für ein punktförmiges Objekt
wie z.B. einen Stern gilt hingegen
Lichtstärke ∝ D2
(3)
Die meisten astronomischen Objekte sind sehr weit entfernt, also punktförmig, so dass
astronomische Teleskope große Durchmesser haben sollten, um möglichst viel Licht
aufzusammeln.
2.2.2
Das Auflösungsvermögen
Die Auflösung astronomischer Teleskope ist durch die Beugung des von den Sternen
ausgesandten kohärenten Lichts begrenzt. Aus der Beugungstheorie erhält man für die
Intensitätsverteilung I(θ) einer kreisförmigen Blende mit Radius r im Winkelabstand θ
(z.B. Born & Wolf, 1980; Kitchin, 1984)
Iθ ∝
π2 r4
(J1 (2m))2
2
m
(4)
wobei
πr sin θ
(5)
λ
und durch J1 (2m) die Besselfunktion erster Art der Ordnung eins bezeichnet wird. In
Abbildung 3 ist J1 (2m)/m dargestellt.
Die Intensität ist also Null in konzentrischen Ringen mit Radius
m=
θ≈
1.220 λ
,
d
2.233 λ
,
d
3.238 λ
,...
d
(6)
wobei d = 2r der Durchmesser des Beugungsscheibchens ist. Die innerste Beugungszone bezeichnet man als Airy-Scheibchen, nach dem englischen Royal Astronomer George B. Airy, der als erster Gleichung 4 hergeleitet hat. Abbildung 4 stellt die AiryScheibchen für zwei gleich helle Punktquellen im Abstand 4.46 λ/d dar. Die Abbildung
eines Sterns mit einem astronomischen Teleskop führt also zu einer ausgedehnten Scheibe mit Radius 1.22 λ/d, die von Beugungsringen umgeben ist.
Zur Charakterisierung der Auflösung eines Teleskops wird meist das von Lord Rayleigh eingeführte Kriterium verwendet. Das Rayleigh-Kriterium besagt, dass zwei gleich
helle Objekte gerade dann noch auflösbar sind, wenn das Intensitätsmaximum der Beugungsfigur des einen Objekts genau in das erste Intensitätsminimum der Beugungsfigur
des zweiten Objekts fällt. Damit ist die Auflösung α gerade
α[rad] =
1.220 λ
.
d
7
(7)
1.0
J1(2m)/m
0.8
0.6
0.4
0.2
0.0
-0.2
0
2
4
6
m
Abbildung 3: Graph der Funktion J1 (2m)/m, deren Quadrat
die Intensitätsverteilung an einer
kreisförmigen Blende beschreibt
(Glg. 4).
Abbildung 4: Beugungsbild zweier gleich
heller Punktquellen im Abstand 4.46 λ/d
an einer kreisförmigen Blende, wie in der
Astronomie üblich als Negativ dargestellt
(schwärzer entspricht also heller).
8
Aufgabe 2: Berechnen Sie die Auflösung in Bogensekunden eines Teleskops mit einem Teleskopdurchmesser von d = 0.8 m bei einer Wellenlänge von 5700 Å.
Wie diese Herleitung zeigt, ist das Rayleigh-Kriterium nur eine grobe Näherung für
das tatsächliche Auflösungsvermögen eines Instruments. Die tatsächlich erreichbare
beugungsbegrenzte Auflösung hängt sehr vom Intensitätsverhältnis der beobachteten
Objekte ab (eine sehr schwache Quelle ist in der Umgebung eines sehr hellen Objekts
natürlich schwerer zu detektieren als ein vergleichsweise helles Objekt). Zusätzlich ist
bei erdgebundener Beobachtung die Erdatmosphäre der eigentlich die Auflösung begrenzende Faktor (siehe Abschnitt 2.2.6). Daher ist für praktisches Arbeiten α ≈ λ/d
eine ausreichende Näherung.
2.2.3
Refraktoren
Mit der Demonstration des Fernrohrs zum “Näherholen” entfernter Gegenstände auf
dem Campanile von San Marco in Venedig am 21. August 1609 durch Galileo Galilei begann die naturwissenschaftliche Nutzung der Teleskope. Galilei hatte Gerüchte
über die Entdeckung eines holländischen Glasmachers, Hans Lippershey, vernommen
und sich ein eigenes kleines Fernrohr durch die Kombination einer Sammel- und einer
Streulinse gebaut. In Verneinung der eigentlichen Urheberschaft dieses Instrumentes
wird die Kombination einer Sammel- und einer Streulinse ein “galileisches Fernrohr”
genannt; seinem geschickten Marketing hatte Galilei eine Gehaltsverdoppelung zu verdanken. Als Alternative zum Galileischen Fernrohr schlug Johannes Kepler in seiner
Dioptrice, 1611, die Kombination zweier Sammellinsen vor, das “keplersche Fernrohr”.
Im Gegensatz zum galileischen Fernrohr besitzt das keplersche eine echte Fokalebene,
d.h. es kann für quantitative astronomische Messungen und nicht nur zur Beobachtung
benutzt werden.
Obwohl sich Refraktoren in einigen Bereichen, zum Beispiel als Feldstecher, durchgesetzt haben, werden Refraktoren in der Astronomie als Instrumente heute nicht mehr
eingesetzt. Der Hauptgrund dafür ist, dass der Maximaldurchmesser eines Refraktors
bei ∼ 1 m liegt, also bei einer vergleichsweise kleinen Lichtsammelfläche. Die Begründung für diesen kleinen Maximaldurchmesser ist, dass größere Linsen nur sehr schwer
herstellbar und im Gebrauch aufgrund ihres hohen Eigengewichtes nur sehr schwer stabilisierbar sind. Bei der Änderung der Pointierungsrichtung eines Teleskops verformen
sich Linsen sehr stark, da sie im Gegensatz zu einem Spiegelsystem nicht unterstützt
werden können – etwas weniger akademisch ausgedrückt bedeutet hier “sehr starke
Verformung” nichts anderes als “zerbrechen”. Ferner muss zur Herstellung einer Linse
großen Durchmessers ein Glasblock entsprechenden Durchmessers ohne Lufteinschlüsse hergestellt werden, was große Kosten verursacht. Desweiteren entspricht die Baulänge eines Refraktors seiner Brennweite, was zu großen, unhandlichen und instabilen
(Durchbiegung!) Instrumenten führt. Schließlich muss auch noch berücksichtigt werden, dass der Brechungsindex von Glas wellenlängenabhängig ist, was zu Bildfehlern
führt (chromatische Aberration).
Aus diesen Gründen haben sich in der Astronomie seit Mitte des 20. Jahrhunderts
Reflektoren auf breiter Linie durchgesetzt. Die in manchen Sternwarten, so auch der
Tübinger Sternwarte, noch vorhandenen Refraktoren haben nur noch Museumswert und
werden für die aktive Forschung nicht eingesetzt2 . Die einzige Ausnahme bildet hierbei
2 Der
Tübinger Refraktor wird in der Öffentlichkeitsarbeit für Sternführungen eingesetzt.
9
die Spezialanwendung der Astrometrie, also der Vermessung von Sternpositionen, bei
der Refraktoren mit typischen Durchmessern < 30 cm als sogenannte Meridiankreise
eine Nische gefunden haben. Auch diese Instrumente wurden seit 1985 mehr und mehr
von satellitengestützten Instrumenten, so zum Beispiel dem europäischen HipparcosSatelliten, ersetzt.
Einen sehr schönen Überblick über den historischen Wettstreit um den weltgrößten
Refraktor gibt der Artikel aus Sterne und Weltraum (August 2011) im Anhang dieser
Anleitung auf Seite 55.
2.2.4
Reflektoren
Wie bereits oben dargestellt, bestehen Reflektoren aus der Kombination eines konischen, fokussierenden Hauptspiegels mit weiteren Spiegeln zur Bestimmung der Lage
des Fokus.
Abbildung 5: Strahlengang des newtonschen Teleskops (Newton, 1730, Fig. 29).
Weit verbreitet in der Amateurastronomie sind Reflektoren mit dem Strahlengang,
der 1671 von Isaac Newton erfunden wurde (Abb. 5). Hier wird das Licht mit einem parabolischen Hauptspiegel fokussiert. Die vom Hauptspiegel kommenden Strahlen werden durch einen zweiten, plan geschliffenen Fangspiegel aus dem Teleskoptubus reflektiert. Der Brennpunkt befindet sich also am Ende des Tubus, weit entfernt vom Hauptspiegel. Dies hat den Nachteil, dass die Baulänge des Teleskops in der Größenordnung
der Brennweite liegt. Ferner müssen die Detektoren weit vom Schwerpunkt des Teleskops entfernt angebracht werden, was mechanisch wenig sinnvoll ist.
Bei neueren Teleskopen haben sich – auch im Amateurbereich – daher andere Strahlengänge durchgesetzt, bei denen das vom Hauptspiegel ausgehende konvergente Strahlenbündel durch einen Fangspiegel auf ein zentrisch im Hauptspiegel angebrachtes Loch
zurückreflektiert wird. Der Fokus befindet sich dann nahe des Hauptspiegels, das heißt
nahe am Schwerpunkt des Teleskops. Ferner ist die Baulänge des Teleskops nur noch
∼ f /2. Eine solche Anordnung bezeichnet man als Cassegrain-Strahlengang.
Allerdings hat auch der Cassegrain-Strahlengang noch den Nachteil, dass der Fokus
nicht ortsfest ist. Mit anderen Worten muss die Instrumentierung am Teleskop selbst angebracht werden, was für schwere Detektoren nicht verwirklichbar ist. In einem solchen
Fall gibt es weitere Teleskopkonstruktionen, bei denen mit verschiedenen Spiegelanordnungen tatsächlich ein raumfester Fokus erreicht werden kann. Daher werden Großteleskope meist mit mehreren möglichen Strahlengängen konzipiert, die je nach Anforde10
Abbildung 6: Spiegelkonfigurationen eines
8 m-VLT-Units. Der “Nasmyth-Fokus” bezeichnet die Lage des raumfesten Brennpunkts bei azimutaler Montierung des Teleskops (siehe Abb. 2.2.5; Quelle: ESO).
rung des Instruments ausgewählt werden können. Abbildung 6 zeigt beispielhaft die bei
den 8 m-Teleskopen des “Very Large Telescope” des Europäischen Süd-Observatoriums
(ESO) verfügbaren Strahlengänge.
Da der Spiegel bei Reflektoren auf der Rückseite unterstützt werden kann, sind seiner maximalen Größe nur technologische, nicht aber prinzipielle Grenzen gesetzt. Diese
Grenzen werden durch das zur Herstellung vorgesehene Material und die bei der Spiegelherstellung eingesetzten Verfahren bestimmt.
Das für den Hauptspiegel verwendete Material ist im Prinzip frei wählbar, da die
Reflektivität des Spiegels durch eine auf die Spiegeloberfläche aufgedampfte Schicht
(meist aus Aluminium) gewährleistet werden kann. Dieses Material sollte möglichst
einfach schleifbar und sehr gut polierbar sein sowie einen kleinen thermischen Ausdehnungskoeffizienten besitzen, um eine stabile Oberflächenform auch während der Temperaturschwankungen der Beobachtungsnacht zu gewährleisten. Aus diesen Gründen
kommen in der Praxis für Teleskopspiegel heute ausschließlich glasartige Substanzen
in Frage3 . Normales (Kron-)Glas wird wegen seines großen thermischen Ausdehnungskoeffizienten dabei nur für Kleinteleskope benutzt, für Teleskope größerer Bauart werden Quarzglas und Glaskeramiken benutzt. Eine klassische in der Astronomie beliebte
Glaskeramik ist Zerodur, das einen fast vernachlässigbaren Ausdehnungskoeffizienten
hat. Unter verschiedenen Markennamen werden solche Glaskeramiken außerhalb der
Astronomie zum Beispiel zur Herstellung von Küchenherden verwendet, die ja auch
3 Einige
Spezialteleskope verwenden als Hauptspiegel ein rotierendes Quecksilberbad. Diese können
natürlich nur für Beobachtungen im Zenit verwendet werden, sind aber um Größenordnungen billiger als
konventionelle Teleskope (zumindest in Ländern mit geringen Umweltauflagen. . . ).
11
bei extremen Temperaturunterschieden nicht durch innere Spannungen zerstört werden
sollen.
Bis in die 1970er Jahre hinein wurden auch große Teleskopspiegel mit konventionellen Methoden hergestellt. Dazu wurde zunächst ein möglichst luftblasenfreier Glasblock
als Ausgangspunkt genommen. Dieser wurde dann mit immer feinerem Schleifpulver
(Korund und -derivate) in die endgültige Spiegelform geschliffen. Den Abschluss dieses
sehr zeitaufwendigen Verfahrens bildete eine Endpolierung auf die notwendige mittlere Oberflächenrauhigkeit der Endoberfläche von wenigen nm (kleiner als die mittlere
Wellenlänge von sichtbarem Licht). “Zeitaufwendig” bedeutet hier einige Jahre.
Ein großer Nachteil dieses klassischen Verfahrens ist, dass der Spiegelrohling beim
Schleifen großen internen Belastungen ausgesetzt ist und daher sowie aus Stabilitätsgründen beim späteren Einsatz eine vergleichsweise große Dicke haben muß. Die dadurch bedingte hohe Masse des Teleskopspiegels führt dazu, dass sich der Spiegel im
Einsatz nur langsam an die Außentemperatur anpasst, und stellt hohe Anforderungen
an die Teleskopmontierung. Bohrungen in der Spiegelrückseite können diese Nachteile zum Teil ausgleichen und zudem die Stabilität des Spiegels gegenüber plastischen
Verformungen erhöhen. Ferner kann beim Spiegelschleifen eine kurze Brennweite nur
schwer erreicht werden, da dafür sehr viel Material vom Spiegelrohling entfernt werden
muss.
Aus diesen Gründen war der maximale Teleskopdurchmesser von den 1930er Jahren bis in die 1980er Jahre hinein auf kleiner als 6 m begrenzt, mit nur zwei Instrumenten mit Durchmessern größer als 4.50 m: dem berühmten 5 m (200 in) Teleskop
auf dem Mt. Palomar bei Los Angeles und dem russischen 6 m-Teleskop im Kaukasus.
Aufgrund großer thermischer Probleme ist letzteres nur zur Spektroskopie verwendbar.
Mit der Entwicklung neuartiger Techniken zur Spiegelherstellung konnte seither der
maximale Spiegeldurchmesser auf ∼10 m vergrößert werden, das heißt, es wurde eine Vervierfachung der Sammelfläche erreicht. Eine dieser Techniken besteht darin, den
Hauptspiegel aus mehreren kleinen Segmenten zusammenzusetzen. Ein Beispiel hierfür sind die zwei Keck-Teleskope auf dem Mauna Kea in Hawaii mit einem effektiven
Teleskopdurchmesser von 10 m (Abb. 7).
Alternative Techniken, bei denen Spiegel großen Durchmessers am Stück hergestellt
werden, basieren im Wesentlichen auf der Tatsache, dass die Oberfläche einer rotierenden Flüssigkeit näherungsweise ein Paraboloid ist, dessen Oberfläche in Zylinderkoordinaten durch
r2 ω2
(8)
z − z0 =
2g
gegeben ist, wobei g die Oberflächenbeschleunigung, ω die Umdrehungsfrequenz und
z0 die z-Koordinate des Scheitelpunktes des Paraboloids ist. Die Oberfläche der rotierenden Flüssigkeit entspricht also schon der angestrebten Teleskopoberfläche. Am MirrorLab der University of Arizona in Tucson unter Roger Angel wurde daher die Methode des sogenannten “Spin Casting” entwickelt. Hier wird das später den Spiegel bildende Material in einem rotierenden Ofen geschmolzen. Die Rotationsgeschwindigkeit
des Ofens bestimmt hierbei die spätere Brennweite des Spiegels, die vergleichsweise
klein sein kann. Durch kontrolliertes Abkühlen des Spiegels bei weiterhin rotierendem
Ofen kann erreicht werden, dass der dabei entstehende Spiegelrohling eine Form hat,
die schon sehr nahe an der endgültigen Spiegelform liegt. Zudem ist der Spiegelrohling weitestgehend frei von inneren Spannungen, so dass wesentlich dünnere und damit
12
Abbildung 7: Der aus Segmenten zusammengesetzte Hauptspiegel
des 10 m-Keck I-Teleskops auf Hawaii (Quelle: W.M. Keck Observatory).
leichtere Spiegel kleiner Wärmekapazität hergestellt werden können. Beispiele für mit
der Technik des Spin Casting hergestellte Spiegel finden sich in den 8 m-Teleskopen des
Very Large Telescope des Europäischen Südobservatoriums.
Aufgabe 3: Mit welcher Winkelgeschwindigkeit (in Einheiten ◦ /s oder sinnvoller) muss ein
Ofen rotieren, um bei einem Spiegel mit 10 m Durchmesser ein Öffnungsverhältnis von
D/ f = 1/5 zu erreichen? Tip: Die Normalform der Parabel kann in einer Form geschrieben werden, die die Brennweite enthält (Bronstein & Semendjajew (1987)):
y=
2.2.5
1 2
x
4f
(9)
Teleskopmontierungen
Nach der Teleskopoptik selbst ist die Montierung eines Teleskops von besonderer Bedeutung. Die Teleskopmontierung hat die Aufgabe, das Teleskop sicher und genau an
jede beobachtbare Stelle des Himmels zu pointieren und dann der Himmelsdrehung
nachzuführen. Genau bedeutet hier, dass jeder sichtbare Himmelsausschnitt mit einer
Genauigkeit im Bereich weniger Bogensekunden wiederholbar erreicht wird.
Die Katalogisierung von Sternen mit Hilfe des in Abschnitt 2.1 beschriebenen äquatorialen Systems ist der erste Schritt. Der zweite besteht darin, die Objekte an einem
Teleskop einzustellen. Traditionell wurden Teleskopmontierungen mit zwei beweglichen Achsen ausgestattet, von denen die eine, die Pol- oder Stundenachse, parallel zur
Erdachse aufgehängt wird und die andere, die Deklinationsachse, senkrecht zur Stundenachse. Eine solche Teleskopmontierung heißt parallaktische Montierung (Abb. 8,
links), wie dies technisch verwirklicht werden kann zeigt Abbildung 9. Da sich der
Himmel scheinbar um die Erdachse dreht, hat ein solcher Aufbau den Vorteil, dass nach
13
Abbildung 8: Parallaktische (links) und azimutale Montierungen (Quelle: Karttunen
et al., 1990, Abb. 3.16).
Abbildung 9: Technische Realisierungen der parallaktischen Montierung: a deutsche
Montierung, b Kniemontierung, c englische Achsenmontierung, d englische Rahmenmontierung und e Gabelmontierung. S bezeichnet die Stundenachse, D die Deklinationsachse, F ist das Fernrohr und G ein eventuell notwendiges Gegengewicht (Quelle:
Weigert & Zimmermann, 1976, S. 109).
14
Abbildung 10: Links: Die azimutale Montierung eines der 8 m-Teleskope der Europäischen Südsternwarte. Rechts: Das fertig aufgebaute 8 m-Teleskop in Chile. Beachten
Sie die Größe der Struktur! (Quelle: ESO).
der Pointierung des Teleskops dieses nur noch mit konstanter Winkelgeschwindigkeit
um die Stundenachse gedreht werden muss.
Da wir uns mit dem Teleskop nicht in einem raumfesten Bezugssytem befinden, benötigen wir für die Einstellung eines Himmelsobjektes nun doch eine Zeitangabe, die
die Drehung des zeitunabhängigen Himmelssystems relativ zum Bezugssystem der Teleskopmontierung beschreibt. Bei der parallaktischen Montierung kann die Deklination
direkt an der Deklinationsachse eingestellt werden. Für den Winkel in der Äquatorebene definieren wir uns den Stundenwinkel (siehe auch Abb. 1). Dieser ist der Winkel
im Uhrzeigersinn, gemessen in Stunden, zwischen dem Meridian (Großkreis von Süden
durch beide Himmelspole) und dem Objekt auf dem Äquator. Der Stundenwinkel für
ein Objekt ist also sowohl orts- als auch zeitabhängig.
Der Stundenwinkel des Frühlingspunktes wird als Sternzeit bezeichnet. Diese beschreibt die wahre Rotation der Erde. Nach einem siderischen Tag hat die gesamte Himmelskugel mit allen Sternen wieder die gleiche Stellung erreicht. Da die Erde während
eines Tages auch ein Stück auf ihrer Bahn um die Sonne zurücklegt, ist ein siderischer
Tag etwas kürzer als ein synodischer Tag, der Zeit zwischen zwei Meridiandurchgängen
der Sonne. Zur Frühlings-Tagundnachtgleiche entspricht Mitternacht 12:00 Uhr Sternzeit, zur Herbst-Tagundnachtgleiche 0:00 Uhr.
Aufgabe 4: Mit welcher Winkelgeschwindigkeit muss ein Teleskop dem Sternhimmel nachgeführt werden, um die Erdrotation auszugleichen? Gehen Sie von einer Jahreslänge
von 365.25 Tagen aus. . . Wie lang ist ein Sterntag? Überlegen Sie sich mit Hilfe der Koordinaten der Objektliste (Tab. 7) einen Beobachtungsplan für die Praktikumsnacht, d.h.
welche Objekte können wann beobachtet werden?
Der Nachteil der auf die Pole ausgerichteten Montierungen ist, dass diese sehr schwer
zu bauen sind, da das Gewicht des Teleskops auf einer unter einem Winkel zur Erdgra15
vitation stehenden Achse lastet. Daher werden moderne Großteleskope heute meist mit
einer sogenannten azimutalen Montierung ausgestattet, bei denen das Teleskop auf einer
in der Senkrechten beweglichen Achse auf einem Drehtisch lagert (Abb. 8, rechts). Der
Name “azimutale Montierung” kommt daher, dass die Teleskopachsen das Instrument
in der Höhe über dem Horizont (engl. “Altitude”) und im Azimut, dem von der NordSüd-Richtung ausgehend am Horizont gemessenen Winkel, bewegen. Der Übergang auf
azimutale Montierungen war aufgrund der Entwicklung sehr gut steuerbarer Schrittmotoren und schneller Computer möglich, da es heute keine Probleme mehr bereitet, ein
Teleskop auch bei gleichzeitiger Drehung um zwei Achsen sicher nachzuführen. Ein
Beispiel für die technische Realisierung einer azimutalen Montierung ist in Abbildung
10 zu sehen.
2.2.6
Aktive und adaptive Optiken
In diesem Abschnitt soll noch kurz auf technologische Entwicklungen, die hauptsächlich seit den 1980er Jahren Einzug in die optische Astronomie gehalten haben, eingegangen werden. Diese Entwicklungen zielen darauf, den Einfluss von Störquellen auf
astronomische Optiken weitestgehend auszugleichen. Solche Störquellen sind insbesondere das durch die Erdatmosphäre verursachte “Zwinkern” der Sterne, das astronomische “Seeing” und die Verformung der Teleskopoptik unter ihrem Eigengewicht.
Seeing und adaptive Optiken Ein großer Nachteil der erdgebundenen Astronomie
ist, dass astronomische Objekte durch die Erdatmosphäre hindurch beobachtet werden
müssen. Kleinste Schwankungen in Temperatur und Druck, normalerweise in Luftzellen
von ∼50 cm Durchmesser, führen zu kleinen Änderungen im Brechungsindex der Luft.
Diese Änderungen führen dazu, dass von einem Stern ausgehende Lichtstrahlen geringfügig andere Wege durch die Erdatmosphäre nehmen – damit ist das Bild eines Sterns
auf dem Erdboden nicht mehr punktförmig, sondern verwaschen. Dieser Effekt, das
astronomische “Seeing”, ist das bekannte Flackern von Sternen, das besonders bei horizontnahen Objekten gut zu beobachten ist. Es führt dazu, dass die effektive Auflösung
großer Teleskope durch die Erdatmosphäre und nicht etwa durch den Teleskopdurchmesser bestimmt ist.
Aufgabe 5: Ab welchem Durchmesser ist dies der Fall, ab welchem Teleskopdurchmesser
wird also die nutzbare Auflösung des Teleskops vom Seeing bestimmt? Nehmen Sie für
diese Abschätzung einen Wert von 0.1 Bogensekunden für das Seeing an.
Der in der Aufgabe genannte Wert von 0.1 Bogensekunden wird nur an den besten
astronomischen Beobachtungsstandorten, zum Beispiel auf Hawaii oder in den chilenischen Anden (Abb. 11) erreicht, wo aufgrund lokaler meteorologischer Bedingungen
eine sehr geringe Luftunruhe herrscht. Zur Erforschung kleinster Strukturen in astronomischen Aufnahmen ist eine effektive Auflösung im Bogensekundenbereich allerdings zu grob, und, wie Sie gerade gezeigt haben, weit von der beugungsbegrenzten
Auflösung der Großteleskope entfernt. Mit konventionellen Teleskopen kann diese nur
im Weltraum erreicht werden (zum Beispiel mit dem Hubble Space Telescope), auf dem
Erdboden muss versucht werden, das Seeing durch direkten Eingriff in die Teleskopoptik zu korrigieren. Diese Korrekturen fasst man unter dem Stichwort “Adaptive Optik”
zusammen.
16
Abbildung 11: Standort des “Very
Large Telescope” auf dem Paranal
nahe Antofagasta in Chile (Quelle:
ESO).
Die oben angesprochenen Schwankungen des Brechungsindex in der Luft führen
dazu, dass eine außerhalb der Erdatmosphäre ursprünglich parallele Wellenfront in der
Atmosphäre verformt wird (Abb. 12, unten). Diese Verformung führt dann zum beobachteten “Flackern” des Sterns. Wäre es möglich, die Verformung der Wellenfront auszugleichen, dann wäre eine wesentlich bessere Abbildungsqualität gewährleistet. Mit
der Entwicklung schneller Elektroniken rückt eine solche Korrektur zunehmend in den
Bereich des technisch Machbaren. Zur Zeit eingesetzte adaptive Optiken analysieren
das Bild einer Testpunktquelle mit Hilfe eines Wellenfrontsensors. Durch kleine Verformungen des Fangspiegels wird dann die Wellenfront wieder “parallelisiert”. Solche
Korrekturen müssen sehr schnell erfolgen und eine Genauigkeit von ∼ λ/2 haben, wo
λ die Wellenlänge des beobachteten Lichts ist. Daher funktionieren sie zur Zeit hauptsächlich im langwelligen Bereich, zum Beispiel bei Beobachtungen im nahen Infraroten. Da die Testpunktquelle hell genug sein muss, um die Verformung der Wellenfront
zu messen, kommt häufig ein “künstlicher Stern” als Testquelle zum Einsatz, der durch
Resonanzübergänge in einer ∼50 km hohen Natriumschicht in der Erdatmosphäre mit
einem auf die NaD-Linie eingestellten Laser erzeugt wird. In Deutschland wird an der
Entwicklung adaptiver Optiken insbesondere am Max-Planck-Institut für Astronomie in
Heidelberg und an der Europäischen Südsternwarte in Garching bei München geforscht.
Erste Systeme sind am Very Large Telescope des ESO und am 10 m Keck Observatory
auf Hawaii in Einsatz.
Aktive Optiken Die Möglichkeit, dünne Spiegel herzustellen, reduziert nicht nur die
Masse des Teleskopspiegels, sondern erlaubt es auch, Ungenauigkeiten in der Teleskopoptik auszugleichen. Diese Ungenauigkeiten entstehen zum Beispiel durch die schon
in Abschnitt 2.2.4 angesprochene Verformung des Teleskopspiegels bei Temperaturänderungen und durch die plastische Verformung des Teleskops und insbesondere des
17
Abbildung 12: Prinzipien der aktiven und adaptiven Optik (Quelle: ESO).
Abbildung 13: Die Spiegelhalterung
eines der 8 m-Teleskope des “Very Large Telescope” mit den aktiven Elementen zur Verformung des
Hauptspiegels (Quelle: ESO).
18
Hauptspiegels während der astronomischen Beobachtungen (Abb. 12, oben). Die Methode der aktiven Optik macht sich die leichte Verformung der dünnen Spiegel zu Nutze, indem sie den Spiegel durch gezielte Verformungen in seiner Idealform hält. Eine
große Zahl (∼ 80–100) sogenannter Aktuatoren auf der Rückseite des Spiegels zieht
und drückt dabei den Spiegel auf die Idealform. Durch ständige Überwachung einer
Referenzpunktquelle, z.B. eines hellen Sterns, kann dadurch die Qualität der Gesamtoptik nahezu ideal gehalten werden. Abbildung 13 zeigt als Beispiel die Spiegelhalterung
eines der Teleskope des VLT.
2.3
Bilddetektoren
Ist das Licht eines astronomischen Objekts einmal mit dem Teleskop gesammelt worden, muss es physikalisch analysiert werden. Auch mit dem Auge sind quantitative
astronomische Messungen möglich, zum Beispiel basiert die in der Astronomie heute
noch verwendete Skala für die Lichtintensität auf der (grob) logarithmischen Empfindlichkeit des Auges. Für genaue Messungen ist das Auge allerdings nicht geeignet. Mit
der Erfindung der Photographie Mitte/Ende des 19. Jahrhunderts gelang es, einen Detektor zu entwickeln, der unabhängig vom individuellen Beobachter ist und der fähig ist,
Licht über einen längeren Zeitraum aufzuintegrieren. Außerdem war es mit der Photographie erstmals möglich, Messungen aufzuzeichnen und später auszuwerten. Aus diesen Gründen waren photographischer Film und Photoplatten bis Ende der 1970er Jahre
der vorherrschende astronomische Bilddetektor, bevor sie nach der Entwicklung elektronischer Detektoren, insbesondere des Charge Coupled Device (CCD), mehr und mehr
verdrängt wurden. Nur noch für einige sehr spezielle Bereiche war die Photographie bis
vor wenigen Jahren noch unentbehrlich, insbesondere weil es möglich war, sehr große
lichtempfindliche Flächen (Photoplatten bis 36 cm×36 cm) herzustellen. Hersteller wie
Kodak sind heute jedoch nicht mehr bereit, für wenige Platten pro Jahr die Produktion
noch aufrecht zu erhalten. In den letzten Jahren wurden Arrays von CCD-Detektoren
entwickelt, die so auch die letzte Anwendung der Photoplatte übernehmen können. Das
CCD ist daher für optische Anwendungen in der Astronomie der Bilddetektor schlechthin.
2.3.1
Grundlagen des CCD
Das Charge Coupled Device wurde 1969 von W.S. Boyle und G.E. Smith von den Bell
Laboratories erfunden, das Patent für das CCD wurde 1974 erteilt. Einen Überblick über
die Entwicklungsgeschichte des CCD gibt McLean (1997).
Das CCD ist ein Halbleiterdetektor, der aus einer zweidimensionalen Anordnung
von Siliziumdioden besteht. Die einfallenden Photonen erzeugen innerhalb des Festkörpers Elektron-Loch-Paare, wenn ihre Energie ausreicht, um die Elektronen vom
Valenz- in das Leitungsband des Halbleiters anzuheben (innerer Photoeffekt), wenn die
Photonenenergie also größer als die Bandlücke des Halbleiters ist. Für einen SiliziumHalbleiter beträgt die Bandlücke 1.12 eV (Tab. 1). Die freigesetzten Ladungen können
an der Grenzschicht zwischen p- und n-dotiertem Silizium durch äußere Spannungen
in Potentialmulden gesammelt werden, um somit ein Ladungsbild über längere Belichtungszeiten aufzubauen. Die erzeugte Ladungsmenge ist dem einfallenden Lichtfluss
auf das betrachtete Bildelement (Pixel) proportional.
19
Tabelle 1: Bandlücken für verschiedene Halbleitermaterialien (nach McLean, 1997,
Tab. 6.2).
Material
CdS
CdSe
GaAs
Si
Ge
PbS
InSb
Temperatur
[K]
295
295
295
295
295
295
295
77
Bandlücke
[eV]
2.4
1.8
1.35
1.12
0.67
0.42
0.18
0.23
Abbildung 14: Schematischer Aufbau und Prinzip des Ausleseverfahrens bei einem dreiphasigen CCD. Die unter den Elektroden angesammelten Ladungen werden durch stufenweise Änderung der an den Pixeln anliegenden Potentiale verschoben (McLean, 1997, Fig. 6.9)
20
Abbildung 15: Vergleich der Effektivität
von Detektoren in der Astrophysik. Die
als Signal auswertbare Lichtmenge in Prozent des einfallenden Lichtes (logarithmische Skala) ist gegen die Wellenlänge aufgetragen.
Aufgabe 6: Schätzen Sie ab, wie viele Elektronen pro Photon bei Licht der Wellenlänge
λ = 4686Å in einem Si-Halbleiter entstehen. Warum ist es nicht möglich, einen solchen
Halbleiter als CCD für Infrarot-Strahlung im K-Band bei λ = 2.2 µm zu verwenden?
Welches Material würden Sie wählen?
Nach Beendigung der Belichtung werden durch geeignetes Verändern der Potentiale
die Ladungsverteilungen der Pixel Zeile für Zeile an den Bildrand geschoben und über
einen Verstärker hintereinander ausgelesen (Abb. 14). Dabei werden die angesammelten Ladungen in Spannungen umgewandelt, die durch einen Analog-Digital-Wandler
digitalisiert und vom Computer als Daten übernommen werden.
Für die Astronomie sind CCD-Chips insbesondere wegen der im folgenden aufgelisteten Eigenschaften interessant:
Effizienz: Der Quantenwirkungsgrad (quantum efficiency) guter CCDs beträgt bis zu
∼100%, das heißt, nahezu 100% aller auf das CCD auftreffenden Photonen werden registriert. Das bedeutet eine etwa hundertfach höhere Empfindlichkeit gegenüber den konventionellen Photoplatten. Abbildung 15 zeigt den Wirkungsgrad
verschiedenartiger Detektoren in Abhängigkeit von der Wellenlänge.
Linearität: Außer der höheren Empfindlichkeit bietet das CCD gegenüber der “normalen” Photographie den Vorteil der Linearität: Die gemessene Ladungsmenge ist
proportional zur Strahlungsintensität. Es ist also nicht nötig, eine Schwärzungskurve zu erstellen (die eine zusätzliche Ungenauigkeit einführt). Die Gewinnung
qualitativ hochwertiger Aufnahmen mit Photoplatten erfordert viel Übung und
Erfahrung. CCDs dagegen sind sehr einfach zu handhaben. Ein weiterer Vorteil
der CCDs liegt darin, dass die Aufnahmen sofort in digitaler Form für die weitere Bearbeitung (Bildverarbeitung) am Computer vorliegen. Photoplatten müssen
entwickelt und für eine Weiterverarbeitung digitalisiert werden.
Spektrale Empfindlichkeit: Gewöhnliche CCD-Chips haben ihre Maximalempfindlichkeit im roten Wellenlängenbereich. (600 nm–700 nm, siehe Abb. 15). Mit speziellen Beschichtungen und durch Verwendung von “back illuminated” CCDs ist
es möglich, den Empfindlichkeitsbereich zu kürzeren Wellenlängen hin auszudehnen. Heute gibt es CCDs, die bis in den Röntgenbereich empfindlich sind.
Geringer Untergrund: Auch ohne Lichteinfall tritt ein sogenannter Dunkelstrom auf,
da eine gewisse Zahl von Elektronen allein aufgrund ihrer thermischen Energie
21
ins Leitungsband gelangt und sich im Bild als Rauschen bemerkbar macht. Der
Dunkelstrom ist daher temperaturabhängig. In der Praxis wird der Dunkelstrom
durch Kühlung des CCD-Chips reduziert. Dies geschieht mit Flüssig-Stickstoff
oder bei einfacheren Kameras mit Hilfe eines Peltier-Elements. Bei modernen
CCDs ist der Dunkelstrom inzwischen so weit reduziert, dass auch sehr lange
Aufnahmen ohne wesentliche Störung möglich sind.
CCDs registrieren auch einfallende hochenergetische Teilchen kosmischen Ursprungs oder von umgebender Radioaktivität. Ein solches Ereignis hinterlässt eine sehr große Ladungsmenge auf dem getroffenen Pixel, so dass dieses für die
laufende Aufnahme nicht mehr verwendbar ist. Diese sogenannten Cosmics sind
die eigentliche Begrenzung bei Langzeitbelichtungen. Belichtungszeiten über eine Stunde sind meist nicht sinnvoll. Längere Aufnahmen müssen in Einzelaufnahmen aufgeteilt werden.
Dynamik: Die minimale messbare Intensität ergibt sich aus dem Dunkelstrom, die maximale messbare Intensität aus dem maximalen Speichervermögen des einem Pixel zugeordneten Potentialtopfs. Für in der Astronomie verwendete CCDs beträgt
dieser dynamische Bereich ungefähr 1000:1, bei einer normalen Photoplatte lediglich 30:1, das heißt, es können auf einer Aufnahme helle (z.B. Sterne oder
helle Nebel) wie auch dunkle Gebiete (z.B. Filamente) quantitativ untersucht werden. Die Bildtiefe des im Rechner repräsentierten Bildes hängt vom verwendeten
Analog-Digital-Wandler ab, dessen Dynamik größer sein sollte als die Dynamik
des CCD. Sie beträgt meist zwischen 16 und 32 bit.
Auslesezeit: Beim Auslesen des Chips muss darauf geachtet werden, dass das registrierte Ladungsmuster nicht verwischt wird. Die Auslesegeschwindigkeit kann
daher nicht beliebig gesteigert werden. Die Auslesezeit der hier verwendeten Kamera beträgt etwa 2–3 s. Für einen großen Chip benötigt man leicht einige Minuten. Zur Registrierung schnellerer Prozesse sind Standard-CCDs daher nicht
geeignet. Für schnelle Photometrie werden daher immer noch fast ausschließlich
Photomultiplier verwendet. Die Entwicklung rauscharmer und schneller Ausleseelektronik ist zur Zeit ein aktuelles Thema. Am Institut für Astronomie und
Astrophysik sind wir z.B. an der Entwicklung der schnellen Ausleseelektronik
für Röntgen-CCDs für Satelliten beteiligt.
2.3.2
CCDs in der Astronomie
Derzeit bestehen astronomische CCDs aus ungefähr 320×512 bis zu 8k×8k Pixeln.
Die typischen Pixelgrößen betragen zwischen 7µm und 20µm. Die Gesamtdetektorfläche ist also im Vergleich zu konventionellen Photoplatten (Größe bis zu 32 cm×32 cm)
sehr klein, das heißt, der abgebildete Himmelsbereich beträgt (an astronomischen Teleskopen) nur bis zu einigen Bogenminuten. Für viele astronomische (Einzel-)Objekte
ist dies jedoch keine Einschränkung, da deren Winkelausdehnung sehr gering ist. Lediglich großflächige Himmelsdurchmusterungen – wie z.B. die Palomar Sky Survey,
die mit Hilfe von Schmidt-Kameras (Bildfeld 6◦ × 6◦ ) gemacht wurde – sind bisher nur
mit erheblichem Aufwand möglich (CCD Arrays). Das räumliche Auflösungsvermögen
wird von der Pixelgröße und vom Abbildungsmaßstab der Optik bestimmt. Um das
22
Auflösungsvermögen des Instruments bei guten atmosphärischen Bedingungen auszunutzen, sollten die einzelnen Pixel weniger als 100 des Himmels abbilden.
Typische Anwendungsgebiete des CCD in der modernen Astronomie sind die Bildgewinnung und die Messung von Sternhelligkeiten (Photometrie). Ferner werden CCDs
als Strahlungsdetektoren in der Spektroskopie eingesetzt:
Bilder werden meist mit Filtern aufgenommen. Im Licht einer einzelnen Emissionslinie aufgenommene Bilder werden beispielsweise dazu benutzt, den Ionisationszustand verschiedener Objekte zu untersuchen.
Spektroskopie: Das CCD dient als hochempfindlicher linearer Detektor, bei dem das
vom Spektrographen erzeugte Spektrum des Objekts auf das CCD abgebildet
wird.
Lichtkurven (CCD-Photometrie): Quantitative Flussbestimmungen aus einer Folge
von CCD-Aufnahmen werden zu einer Lichtkurve zusammengesetzt.
Positionsmessung (Astrometrie) dient zur Messung von Winkelabständen von Himmelskörpern anhand von Bildern.
In diesem Versuch werden wir exemplarisch die ersten beiden oben aufgelisteten Punkte
behandeln.
2.4
Spektroskopie
Die Aufgabe eines Spektrographen besteht darin, die Intensitätsverteilung des Lichts
als Funktion der Wellenlänge darzustellen. Während beim Prismenspektrographen das
Spektrum durch Lichtbrechung entsteht, erfolgt dies beim Gitterspektrographen durch
Lichtbeugung. Dabei muss der Spektrograph so effizient wie möglich sein, da die Lichtquellen sehr schwach sein können.
Moderne Spektrographen werden heutzutage fast ausschließlich mit einem Gitter
anstatt eines Prismas als dispergierendem Element gebaut, da ein Prismenspektrograph
eine ungleichförmige Dispersion zeigt, während sie beim Gitterspektrographen in guter
Näherung linear ist. Darüberhinaus werden anstelle von lichtdurchlässigen Gittern meist
Reflexionsgitter verwendet, mit welchen die Interferenzen des reflektierten anstatt des
transmittierten Lichtes beobachtet werden.
Es gibt mehrere Vorteile der Reflexionsgitter gegenüber Transmissionsgittern: Zum
einen wird bei einem Reflexionsgitter verhindert, dass Licht ein von Luft verschiedenes Medium passieren muss und dadurch Störungen des Spektrums durch chromatische
Aberration auftreten. Desweiteren sind Reflexionsgitter einfacher und damit billiger herzustellen. Der Hauptvorteil der Reflexionsgitter liegt aber vor allem darin, dass sie “geblazed” werden können, das heißt, dass ein großer Teil des zur Verfügung stehenden
Lichts in eine Ordnung gebeugt werden kann. Dieses Verfahren ermöglicht daher eine
beachtliche Verringerung von Lichtverlusten am Beugungsgitter.
Für die Qualität eines Spektrographen sind vor allem die folgenden zwei Kriterien
ausschlaggebend: Zum einen sorgt eine hohe Winkeldispersion für ein möglichst weit
auseinander gezogenes Spektrum. Zum anderen bestimmt das Auf lösungsvermögen eines Gitters, ob zwei eng benachbarte Spektrallinien gerade noch trennbar sind. Im Folgenden wird die Beugungstheorie des Gitters besprochen, um danach auf die beiden
23
Abbildung 16: Geometrie der Beugung am
Doppelspalt: benachbarte Ordnungen liegen um λ/a = sin β − sin ε auseinander; a
ist der Abstand der parallelen Gitterstriche,
ε der Einfallswinkel und β der Ausfallswinkel (Schmidt, 1995)
Qualitätspunkte Dispersion und Auflösungsvermögen näher einzugehen. Als weiterführende Literatur sei auf Schmidt (1995) und Staudt (1993) verwiesen.
2.4.1
Beugungstheorie am Gitter
Die Beugungstheorie eines Reflexionsgitter entspricht der eines Transmissionsgitters.
Zur besseren Veranschaulichung wird im Folgenden die Beugungstheorie anhand eines
Transmissionsgitters beschrieben. Entsprechend Abbildung 16 ergeben sich am Beugungsgitter Intensitätsmaxima, wenn der Gangunterschied ∆ = a (sin β − sin ε) benachbarter Strahlen einem ganzzahligen Vielfachen n der Wellenlänge λ entspricht:
sin β − sin ε =
nλ
a
(10)
Benachbarte Ordnungen liegen um sin β − sin ε = λa auseinander. Somit ist die Lage
der jeweiligen Hauptmaxima bei der Interferenz monochromatischen Lichtes der Wellenlänge λ an einem Gitter unabhängig von der Anzahl der Gitterspalte N, wohl aber
abhängig von der jeweiligen Wellenlänge des verwendeten Lichtes. Das Maximum erster Ordnung für langwelliges Licht entsteht somit unter größerem Winkel als jenes für
kurzwelliges Licht. Zwischen den Hauptmaxima erhält man entsprechend Abbildung
17 jeweils N − 2 kleine Nebenmaxima, die mit zunehmender Spaltenzahl N schwächer
werden, was gleichzeitig zur Folge hat, dass sich die Linienschärfe der Hauptmaxima
erhöht.
Bei den bisherigen Überlegungen wurde davon ausgegangen, dass die einzelnen Gitterspalte beliebig schmal seien und daher nur eine Elementarwelle von ihnen ausginge.
Dies ist in der Praxis jedoch nicht der Fall: die Kugelwellen, welche von einem Gitterspalt ausgehen, interferieren zusätzlich miteinander. Dadurch wird das Interferenzbild
eines Gitters durch das eines Einzelspaltes moduliert. Die Funktion des Interferenzbildes am Einzelspalt wird dann zur Einhüllenden des Gitterinterferenzbildes, so dass
die Hauptmaxima des Gitters unterschiedliche Intensitäten haben. Zum Beispiel können
Gittermaxima an der Stelle eines Minimums vom Einzelspalt völlig ausgelöscht werden.
Vor allem aber enthält das Maximum nullter Ordnung, welches keine Beugungsinformation enthält, die größte Lichtmenge.
24
Abbildung 17: Beugung am Gitter; n = ±1, ±2, ±3, . . .: Ordnung des Spektrums ; g:
Abstand der parallelen Gitterstriche; α: Ausfallswinkel, ∆: Gangunterschied (Staudt,
1993)
Bei einem Reflexionsgitter kann man dies umgehen, indem die einzelnen Spalte
entsprechend Abbildung 18 als keilförmige Stufen mit dem Blazewinkel Θ ausgeführt
werden, so dass die auf die unterschiedlichen Stufen eintreffenden Strahlen mit einem
Gangunterschied ∆ = na sin(Θ + δ) reflektiert werden. Maxima n-ter Ordnung entstehen, analog zum normalen Gitter, wenn der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge beträgt. Somit kann die Hauptmenge des Lichtes, welche ursprünglich keine Information enthielt, als Informationsträger genutzt werden.
Zur Bestimmung des mit einem Blazegitter beobachtbaren Spektralbereichs betrachten wir zunächst den Fall einer monochromatischen Lichtquelle. Fällt Licht mit der Wellenlänge λB unter dem Einfalls- bzw. Ausfallswinkel δ auf die Blaze-Spiegelflächen, so
gilt
ε = δ−Θ
und
β = Θ+δ
(11)
und daher
∆ nλB
=
= sin(Θ + δ) = sin(2Θ + ε)
(12)
a
a
Damit stehen die Wellenlänge λB , der Reflexionswinkel δ und der Blazewinkel Θ in
enger Beziehung zueinander. Durch minimale Änderung des Reflexionswinkels δ verschiebt sich die Lage der Spektrallinie innerhalb einer Ordnung entsprechend. Durch
eine Änderung des Einfallswinkels durch Drehen des Gitters im Strahlengang ist es also
möglich, abschnittweise einen sehr breiten Wellenlängenbereich zu detektieren.
Für nicht-monochromatisches Licht ist die Intensitätsverteilung des Spektrums durch
die Beugung am Gesamtgitter bestimmt. Diese Verteilung bezeichnet man als die Blazefunktion des Blazegitters. Ihre Breite bei halber Intensität ist als sogenannter nutzbarer
Wellenlängenbereich λ/b definiert (Abb. 19). Es gilt
∆λ =
λB
n
(13)
wobei n die Beugungsordnung und die Blazewellenlänge λB die zentrale Wellenlänge
ist. Ein maximal großer nutzbarer Wellenlängenbereich ergibt sich daher bei n = 1.
25
einfallender
Strahl
G
G
N
N
N
ε
reflektierter
Strahl
β
−δ
δ
Θ
δ
Θ
.
∆
.
Θ+δ
.
.
Θ
a
.
a
Abbildung 18: Strahlengang am Blazegitter: eintreffende Strahlen werden mit einem
Gangunterschied ∆ = na sin(Θ + δ) reflektiert, G: Gitternormale, N: Spiegelflächennormale, Θ: Blazewinkel, δ: Ein- bzw. Ausfallswinkel
Abbildung 19: In “erster Ordnung geblazedes” Gitter (Schmidt, 1995).
26
2.4.2
Die Dispersion
Die Dispersion ist ein Maß dafür, um welchen Wellenlängenanteil sich das Spektrum
einer Ordnung mit zunehmendem Winkel ändert. In der folgenden Herleitung sei der
Einfachheit halber der Einfallswinkel gleich Null. Beugungsmaxima entstehen nach
Gleichung 10 dann für
a sin β
.
(14)
λ=
n
wobei β der Ausfallswinkel, a der Abstand der Gitterstriche und n die Ordnung des
Spektrums ist. Damit ist
dβ
n
=
(15)
dλ a cos β
Da β im Allgemeinen klein und damit cos β ≈ 1 ist, bleibt daher die Dispersion innerhalb
einer Ordnung praktisch konstant. Dies ist ein entscheidender Vorteil des Dispersionsgitters gegenüber dem Prisma, welches eine nichtlineare Dispersion zeigt. Üblicherweise wird die Dispersion in Å/mm angegeben.
2.4.3
Das Auflösungsvermögen
Zur Herleitung der spektralen Auflösung eines Spektrographen geht man von der Annahme aus, dass die Intensitätsverteilungen zweier Linien mit den Wellenlängen λ und
λ + ∆λ gerade dann noch getrennt wahrgenommen werden können, wenn das Hauptmaximum der einen Linie mit dem ersten Minimum der anderen Linie zusammenfällt. Das
Verhältnis
λ
(16)
A=
∆λ
wird als das Auflösungsvermögen des Spektrographen bezeichnet. Für einen Gitterspektrographen erhält man
λ
= Nn
(17)
∆λ
wobei N die Zahl der Gitterstriche und n die Beugungsordnung ist.
Das spektrale Auflösungsvermögen hängt somit theoretisch nur von der zu analysierenden Ordnung und der Anzahl der Gitterstriche des Beugungsgitters ab. Praktisch
wird die spektrale Auflösung eines Spektrographen allerdings zusätzlich von einer Reihe von Faktoren beeinträchtigt. Neben den Eigenschaften des Gitters sind dies insbesondere die Auflösung der optischen Anordnung des Spektrographen und die Breite des
Eintrittsspaltes. Auf diese Punkte soll hier jedoch nicht weiter eingegangen werden.
2.5
Strahlungstheorie
Die elektromagnetische Strahlung eines astronomischen Objektes ist die wesentliche
Informationsquelle, die uns für eine Untersuchung der physikalischen Eigenschaften zur
Verfügung steht. Für die folgenden Aufgaben benötigen wir daher eine Beschreibung
des Strahlungsfeldes.
27
Abbildung 20: Definition der Intensität (Quelle:
Unsöld & Baschek, 1988, Abb. 4.2.1).
2.6
Strahlungsintensität und Strahlungsfluss
Betrachten wir eine strahlende Fläche wie z.B. die Oberfläche eines Sterns, dann ist die
Intensität Iν die Energie ∆E des Strahlungsfeldes, die im Frequenzintervall [ν, ν + ∆ν],
im Zeitintervall [t,t + ∆t] in den Raumwinkel ∆ω um die Flächennormale ~n und durch
das Flächenelement senkrecht zu ~n am Ort~r mit der Fläche ∆A verläuft (Abb. 20):
Iν (ν,~n,~r,t) :=
∆E
∆ν∆t∆ω∆A cos ϑ
Der Strahlungsfluss Fν in Richtung ~n ergibt sich aus der Integration über alle Raumwinkel:
Z Z
2π
π
Fν =
0
Iν cos ϑ sin ϑdϑdϕ
0
Für ein isotropes Strahlungsfeld ist der Strahlungsfluss also gleich Null. Auf der
Sternoberfläche kommt die Strahlung nur aus einer Hemisphäre (aus dem Sterninneren),
Einstrahlung von außen kann abgesehen von sehr engen Doppelsternen vernachlässigt
werden. Die Ausstrahlung eines Sternes ist also:
Fν+ =
Z π/2 Z 2π
0
0
Iν cos ϑ sin ϑdϑdϕ
Die mittlere Intensität I¯ν einer projizierten Sternscheibe ist gegeben durch (Abb. 21):
2
πR I¯ν =
Z 2π Z π/2
0
0
Iν (ϑ, φ)R2 cos ϑ sin ϑdϑdϕ
Kürzt man mit R2 und vergleicht mit der Definition der Ausstrahlung, dann ist
πI¯ν = Fν+ ,
28
Abbildung 21: Mittlere Intensität einer Sternscheibe (Quelle: Unsöld & Baschek, 1988,
Abb. 4.2.3).
d.h., die mittlere Intensität der Sternscheibe ist proportional zum Strahlungsfluss an der
Sternoberfläche. Befindet sich der Stern (Radius R) in einer großen Entfernung r vom
Beobachter, so gilt für den im Detektor registrierten Strahlungsstrom fν :
fν = Fν R2 /r2 .
Die Intensität der Gesamtstrahlung I sowie der Gesamtstrahlungsfluss F ergeben sich
aus der Integration über alle Frequenzen.
2.6.1
Strahlung im thermodynamischen Gleichgewicht
Die Intensität eines Gases im thermodynamischen Gleichgewicht lässt sich durch die
plancksche Strahlungsformel angeben (Strahlung eines „schwarzen Körpers“, Abb. 22):
Bν (T ) =
1
2hν3
.
2
c ehν/kT − 1
Die gesamte Ausstrahlung lässt sich also schreiben als
Abbildung 22: Planckfunktion, wiensches Verschiebungsgesetz.
F + = πB(T ),
und ist nach dem stefan-boltzmannschen Strahlungsgesetz proportional zur vierten Potenz der Temperatur:
F + = πB(T ) = σT 4
mit der Strahlungskonstante σ = 5.67 · 10−8W m−2 K −4 = 5.67 · 10−5 erg s−1 cm−2 K−4 .
29
2.6.2
Effektivtemperatur und Leuchtkraft
Sterne sind nicht im thermodynamischen Gleichgewicht, die Energieverteilung entspricht
daher auch nicht der eines schwarzen Körpers. Die plancksche Strahlungsformel kann
aber trotzdem zur groben Beschreibung herangezogen werden. Aus dem Vergleich des
Gesamtstrahlungsstroms eines Sternes mit dem eines schwarzen Körpers kann man die
Effektivtemperatur definieren:
4
σT 4 = πB(T ) = F = σTeff
Die Effektivtemperatur eines Sternes ist also die Temperatur, die ein schwarzer Körper
haben müsste, um die gleiche Energie pro Fläche und Zeiteinheit abzustrahlen.
Die gesamte Energie pro Zeiteinheit, die von einem Stern emittiert wird, die Leuchtkraft, ergibt sich durch die Multiplikation des Gesamtstrahlungsstroms mit der Sternoberfläche:
4
.
L = 4πR2 F = 4πR2 σTeff
2.6.3
Helligkeiten und Farben
Die astronomische Helligkeitsdefinition orientiert sich einerseits an der logarithmischen
Empfindlichkeit des Auges und andererseits an der antiken Helligkeitseinteilung von
Hipparch. Die scheinbare Helligkeit eines Objekts mit dem Strahlungsstrom s1 relativ
zu einem Strahlungsstrom s2 ist definiert als:
m1 − m2 = −2.5 log(s1 /s2 ).
Beispiele sind Wega (α Lyr) mit einer visuellen Helligkeit von 0.m 14, Sirius mit −1.m 6
und die Sonne mit −26.m 8. Neben der spektralen Energieverteilung eines Objektes hängt
die Helligkeit auch noch von dem Empfindlichkeitverlauf des Instruments ab. Idealerweise hängt diese wiederum nur von dem verwendeten Filter ab. Helligkeitsangaben in
den verschiedenen Filtern werden mit einem entsprechenden Index gekennzeichnet. Wir
verwenden ein Filtersystem, das sich an das von Johnson und Morgan definierte anlehnt
(Abb. 23).
U Ultraviolett: λeff = 3500 Å
B Blau: λeff = 4350 Å
V Visuell: λeff = 5550 Å
R Rot: λeff = 7100 Å
I Infrarot: λeff = 9700 Å
Die Differenz aus zwei Filterhelligkeiten wird als Farbe bezeichnet, wobei immer
mkurzwellig − mlangwellig angegeben wird. Wegen der relativen Definition der Helligkeiten
können wir den Nullpunkt wählen. Dieser ist auf Wega bezogen, die in allen Farben den
Wert 0 haben soll.
30
Abbildung 23: Filterfunktionen des JohnsonSystems (U, B,V, R, I) (Quelle: Unsöld & Baschek, 1988, Abb. 4.4.1).
2.7
Farben-Helligkeits-Diagramm
Das Farben-Helligkeits-Diagramm (FHD, Abb. 24) ist das Fundamentaldiagramm der
stellaren Astrophysik. Die Farbe ist ein Maß für die Effektivtemperatur.
Aufgabe 7: Erklären Sie mit Hilfe von Schwarzkörper-Sternen den Zusammenhang von Farbe
und Temperatur. Warum gibt es bei sehr heißen Sternen keine Farbänderung mit der
Temperatur mehr?
Die Helligkeit ist ein Maß für die Leuchtkraft, hier geht aber auch die Entfernung ein.
Erstellt man ein Farben-Helligkeits-Diagramm eines Sternhaufens, sind die Helligkeitsunterschiede zwischen den Sternen direkt ein Maß für die Leuchtkraftunterschiede, da
alle Sterne in erster Näherung gleich weit entfernt sind (die Haufenausdehnung ist viel
kleiner als die Haufenentfernung).
Abbildung 24: Farben-Helligkeits-Diagramm
(Quelle: Unsöld & Baschek, 1988, Abb. 4.5.2).
Das Farben-Helligkeits-Diagramm ist äquivalent zum Hertzsprung-Russell-Diagramm
(HRD), wo der Spektraltyp (s.u.), der ebenfalls ein Maß für die Effektivtemperatur
ist, gegen die Helligkeit aufgetragen ist. Eine weitere Variante stellt das physikalische
Hertzsprung-Russell-Diagramm mit Effektivtemperatur und Leuchtkraft als Achsenparametern dar. Sterne nehmen im HRD bzw. FHD charakteristische Positionen ein. Vergleiche von Sternpositionen im HRD mit theoretischen Entwicklungsrechnungen erlauben z.B. die Bestimmung des Entwicklungszustandes eines Sterns. Da Sterne in Sternhaufen alle gleich alt sind, erlaubt der Vergleich des FHDs des Haufens mit theoretischen FHDs (Isochronen) eine Altersbestimmung. An dieser Stelle lohnt es sich, den
sehr schönen Artikel über offene Sternhaufen aus Sterne und Weltraum (August 2011)
auf Seite 65 im Anhang dieser Anleitung zu lesen.
31
2.8
Spektralklassen
Sternspektren spiegeln die physikalischen Bedingungen in der äußeren Hülle wider.
Durch Vergleich von beobachteten Spektren mit theoretischen kann man z.B. die Effektivtemperatur, die Oberflächenschwerebeschleunigung und die chemische Zusammensetzung bestimmen. Dies erlaubt, bei bekannter Entfernung, z.B. die Einordnung ins
HRD. Um nicht bei jedem neuen Stern eine detaillierte Spektralanalyse durchführen zu
müssen, ist eine Klassifikation der Sternspektren sinnvoll. Neue Objekte müssen dann
nur in dieses Schema eingeordnet werden, um deren Parameter bestimmen zu können.
Abbildung 25: Schematisches HRD mit Leuchtkraftklassen (Quelle: Karttunen et al., 1990,
Abb. 9.9).
Gebräuchlich ist heute die Spektralklassifikation nach Morgan und Keenan, die eine
zwei-parametrige Klassifikation (Abb. 25) nach Spektraltyp und Leuchtkraftklasse definiert haben. Der Spektraltyp wird nach der Havardklassifikation mit den Buchstaben O,
B, A, F, G, K und M gekennzeichnet, wobei jede Spektralklasse noch in zehn Unterklassen von 0 bis 9 unterteilt wird. In jüngster Zeit ist die Einführung von zwei weiteren
Spektralklassen, L und T, für sehr rötliche Objekte notwendig geworden. Die Einteilung
in die Klassen erfolgt über die Vermessung von Linienstärken verschiedener Spektrallinien (Abb. 26). Der Spektraltyp ist ein direktes Maß für die Effektivtemperatur.
Aufgabe 8: Welcher Effektivtemperatur entspricht die Spektralklasse B, welcher M? Wieso
nimmt die Stärke der Balmerlinien mit zunehmender Effektivtemperatur erst zu und
dann wieder ab (Abb. 27)?
Der zweite Parameter, die Leuchtkraftklasse (I: Überriesen bis V: Zwerge) orientiert
sich an den Linienbreiten. Bei gleichem Spektraltyp nimmt z.B. die Linienbreite der
Balmerlinien mit abnehmender Leuchtkraftklasse ab.
Aufgabe 9: Welches ist die Spektralklasse der Sonne?
32
Abbildung 26: Spektralklassifikation (Quelle:
Seeds, 1997, Abb. 7-16).
Abbildung 27: Linienstärken verschiedener
Elemente in Abhängigkeit von der Temperatur.
33
3
Versuchsaufbau
Die Spektroskopie von Sternen werden wir mit dem 10 C-Reflexionsspektrographen
am 0,8 m-Reflektor des Instituts für Astronomie und Astrophysik, Abteilung Astronomie, durchführen. Der Versuchsaufbau besteht aus dem 0,8 m-Reflektor, dem 10 CReflexionsspektrographen und einer CCD-Kamera, die als Detektor für das aufgenommene Spektrum dient. In den nächsten Abschnitten werden Sie diese Komponenten genauer kennenlernen.
3.1
Spiegelteleskop
Abbildung 28: Der Tübinger 0,8m Reflektor.
Das Tübinger 0,8 m-Spiegelteleskop (Tab. 2) wurde 2003 von der Firma Astro Optik Philipp Keller hergestellt und montiert, es befindet sich in einer 5 m durchmessenden Kuppel der Firma Baader (Abb. 28). Das Teleskop ist parallaktisch in einer Gabel montiert, besitzt einen Friktionsantrieb und ist vollständig computergesteuert. Die
Nachführung wird zusätzlich durch hochauflösende Encoder in Echtzeit korrigiert. Allerdings liegt aufgrund der extrem präzisen Mechanik auch ohne Encoder der RMSNachführfehler bereits weit unter einer Bogensekunde pro Minute. Nähere Informationen finden sich unter http://www.astrooptik.com.
34
Tabelle 2: Technische Daten des Tübinger 0,8 m-Reflektors.
Öffnung D
Brennweite f
Öffnungsverhältnis f /D
Hauptfernrohr
800 mm
6400 mm
8
Abbildung 29: Aufbau des 10 C Spektrographen Quelle: (Optomechanics Research,
1997).
3.2
Der 10 C-Gitterspektrograph
Bei dem in Tübingen verwendeten Spektrographen handelt es sich um einen 10 CReflexionsgitterspektrographen der Firma Optomechanics Research, Inc., Vail, Arizona
(Abb. 29, Tab. 3).
Die Eintrittsspaltanordnung des Spektrographen besteht aus drei Einzelspalten. Durch
den mittleren, etwas längeren Spalt tritt das Licht, welches von dem zu untersuchenden
Objekt (z.B. Sonne, Stern, Flatfield) ausgesandt wird, ein. Zu beiden Seiten des Zentralspaltes ist jeweils ein kürzerer Spalt mit derselben Breite wie der Hauptspalt angebracht.
Es stehen zwei Spaltanordnungen unterschiedlicher Breite (50 µm und 100 µm) zur Verfügung. Das Licht der Vergleichslampen tritt mittels einer optischen Anordnung, bestehend aus Linse, Umlenkspiegel und Lichtleitern, auf die beiden Nebenspalte. Damit
kann simultan zum Spektrum des astronomischen Objekts das Spektrum einer bekannten Quelle aufgenommen werden. Dieses Spektrum kann dann zur Wellenlängenkalibration des astronomischen Spektrums verwendet werden. Am Tübinger Spektrograph
werden als Vergleichslampen eine Quecksilber- und eine Neon-Lampe verwendet. Abbildung 30 zeigt das Emissionslinienspektrum dieser Lampen. Tabelle 8 auf S. 51 im
Anhang listet die genaue Lage der Emissionslinien der Kalibrationslampen auf. Astronomischer Konvention entsprechend werden dabei die Ionen mit römischen Zahlen numeriert: Hg I entspricht also neutralem Quecksilber, Hg II entspricht Hg+ und so weiter.
Hinter der Spaltanordnung befindet sich ein Blaufilter, welcher durch einen Filterschieber wahlweise aus dem Strahlengang genommen werden kann. Er ist im Wellen35
Tabelle 3: Technische Daten des 10 C-Gitterspektrographen.
Gewicht
Kamera
Brennweite
Öffnungsverhältnis
Kollimator
Brennweite
Hauptspalt
Abmessungen
∼ 4.5 kg
f = 135 mm
f /D = 2.8
f = 225 mm
50 µm × 1.5 mm
100 µm × 1.5 mm
Neigung gegenüber der opt. Achse 35◦
Projektion auf Kamera
40 µm bzw. 80 µm
900 µm = 100 pixel
Nebenspalte
Abmessungen
Breite wie Hauptspalt ×0.75 mm
Projektion auf Kamera
455 µm ∼ 50 pixel
Gitter 1
Abmessung
25 mm × 25mm
Linienzahl
g1 = 600/mm
Maximum 1. Ordnung
5000 Å
Dispersion
1.04 Å/pixel
¯
∆λ
5.97 Å
λ/∆λ
840 bei 5000 Å
Überlappung
300 Å
Gitter 2
Abmessung
25 mm × 25mm
Linienzahl
g2 = 1200/mm
Maximum 1. Ordnung
5000 Å
Dispersion
0.54 Å/pixel
¯
∆λ
2.85 Å
λ/∆λ
1754 bei 5000 Å
Überlappung
160 Å
Hg Vergleichslampe
Typ
Osram Hg 100
Brennspannung
45 V
Betriebsstrom
1A
Leistung
22. . . 44 W
Ne Vergleichslampe
Typ
Osram Ne/10
Brennspannung
30 V
Betriebsstrom
1A
Leistung
30 W
Blaufilter
Opazität
5100 Å–5500 Å
Linienfreiheit
in 1. Ordnung < 7500 Å
Abmessungen
12.5 mm× 16.5 mm × 3 mm
36
log relativer Fluß
2
1
0
4000
Hg 4078
Hg 4047
Hg 4358
4500
5000
5500
o
Wellenlänge/A
Hg 4916
Ne 5330/41
Ne 5400
Hg 5461
Hg 5770
Hg 5791
Ne 5852
Ne 5881
6000
Abbildung 30: Hg/Ne-Kalibrationsspektrum, aufgenommen mit dem 1200er Gitter.
Ne 4314
Ne 5944
Ne 5975
Ne 6029
Ne 6074
Ne 6096
Ne 6143
Ne 6164
Ne 6217
Ne 6266
Ne 6305
Ne 6334
Ne 6383
Ne 6402
6500
Ne 6506
Ne 6532
Ne 6599
Ne 6678
Ne 6717
37
Tabelle 4: Technische Daten der STL-1001E Kamera.
Format
1024 × 1024 pixel
Pixelgröße 24 µm × 24 µm
Chipgröße 24,5 mm × 24,5 mm
Kühlung
∆T = 40◦ C
Tabelle 5: Technische Daten der HX916 Kamera.
Format
Pixelgröße
Chipgröße
1300 × 1030 pixel
6,7 µm × 6,7 µm
8,7 mm × 6,9 mm
längenbereich unterhalb von 5100 Å opak, also lichtundurchlässig, während er 90 % der
Strahlung oberhalb von 5500 Å transmittiert. Mit dem Blaufilter wird bei einer Wellenlänge oberhalb von 7500 Å eine Kontamination der Linien erster Ordnung durch jene
zweiter Ordnung vermieden.
Der 10 C-Gitterspektrograph ist mit zwei Blazegittern ausgestattet, welche Gitterkonstanten von g1 = 600/mm und g2 = 1200/mm haben. Das von diesen Gittern erzeugte Spektrum wird schließlich mit einer Kameralinse auf den zur Detektion des
Spektrums verwendeten CCD-Detektor der Kamera HX916 gelenkt.
3.3
CCD-Kameras STL-1001E und HX916
Die am 0,8 m-Teleskop als abbildendes Instrument und Detektor für den Spektrographen
eingesetzten CCD-Kameras sind handelsübliche Kameras vom Typ STL-1001E (Tab. 4)
der kalifornischen Santa Barbara Instrument Group (SBIG) bzw. HX916 (Tab. 5) von
Starlight XPress. Die CCD wird mit einem Peltier-Element gekühlt. Am CCD-Chip lassen sich so ca. 30-40◦ C unter der Umgebungstemperatur erreichen. Die Belichtungszeit
lässt sich von 0.01 s bis 3600 s mit einer Genauigkeit von 0.01 s einstellen und wird
durch einen mechanischen Shutter realisiert. Die Bedienung der Kamera erfolgt über
MaximDL.
38
“My dear Watson, try a little analysis
yourself”, said he, with a touch of
impatience. “You know my methods.
Apply them, and it will be instructive
to compare results”.
Conan Doyle
The Sign of the Four
4
4.1
Versuchsdurchführung
Vorbereitung
Diskutieren Sie die in den vorherigen Abschnitten beschriebenen Grundlagen:
• Koordinatensysteme
• Aufbau astronomischer Teleskope
• Eigenschaften und Vergleich verschiedener Bilddetektoren
• Prinzip des CCD
• Prinzip des Gitterspektrographen
• Farben-Helligkeits-Diagramm
• Spektralklassifikation
Um es noch einmal zu wiederholen: Lösen Sie die in die vorherigen Abschnitte eingestreuten Aufgaben vor dem Versuch und bringen Sie ihre Lösungen am Tag der Versuchsdurchführung mit!
Das Praktikum besteht aus zwei Teilen. Der erste Praktikumstag bzw. -abend ist
der Datenaufnahme gewidmet. Zu diesem Termin sollten Sie bereits Kenntnis über den
allgemeinen Inhalt des Versuchs sowie das verwendete Teleskop haben. Da wir nicht
viele brauchbare Beobachtungsnächte zur Verfügung haben, müssen wir jede zur Verfügung stehende Nacht nutzen. Das erfordert von Ihnen und von uns ein hohes Maß an
Flexibilität. Denken Sie bitte - insbesondere im Winter - auch an ausreichend warme
Kleidung.
Am zweiten Tag beschäftigen wir uns nach einem Testat, bei dem wir auch die
von Ihnen mitgebrachten Aufgaben und eventuell noch ungeklärte Fragen besprechen,
mit der Datenauswertung: Wir werten die Spektren und die Photometrie aus. Gleich zu
Beginn schon der Hinweis, dass Sie sich Mehrarbeit ersparen, wenn Sie bei der Auswertung die folgenden Punkte berücksichtigen:
• Ziehen Sie die sich öffnenden Plotfenster nicht mit der Maus größer/kleiner.
• Schließen Sie diese Fenster nicht einfach.
• Denken Sie daran, Dezimalzahlen mit Punkten, nicht Kommas, zu trennen.
• Kein close_print ohne vorigen open_print-Befehl; ansonsten müssen Variablen eventuell neu gesetzt werden.
• Die für die Photometrie verwendete Routine kennt kein Zurück. Sorgfältiges Arbeiten hilft, nicht von vorne beginnen zu müssen.
39
Im Folgenden stellen wir die einzelnen Arbeitsschritte dar. Sie sollten diesen Abschnitt gelesen haben, so dass Sie die Reihenfolge der Arbeitsschritte verstehen. Die
aufgelisteten Programmbefehle dienen als Referenz für die Versuchsausführung, Sie
müssen sie jetzt noch nicht verstehen oder gar auswendig lernen!
4.2
Sternspektroskopie
Zur Aufnahme der Sternspektren wird der in 3.1 beschriebene 0,8 m-Reflektor mit dem
10 C-Spektrographen und der Kamera HX916 verwendet. Dieses Teleskop befindet sich
in der Beobachtungskuppel auf dem Gelände des Instituts. Die Vorbereitung der Beobachtung wird an Ort und Stelle erklärt, dazu gehören:
1. Vorbereitung des Teleskops und Spektrographen
2. Vorbereitung der Kuppel
3. Vorbereitung der Rechner
Das Programm MaximDL dient einerseits zur Steuerung der Kamera (Belichtung, Kühlung, usw.), andererseits sind damit auch einige Datenreduktionen machbar. Im Praktikum werden mit diesem Programm die Belichtungen durchgeführt, während die Auswertungen der aufgenommenen Bilder mit einem speziellen Bildverarbeitungsprogramm
(IDL) erfolgen. Zum Hochfahren des CCD sind die folgenden Schritte durchzuführen:
1. Das Programm MaximDL starten. Es kann einige Sekunden dauern, bis die Verbindung zum CCD hergestellt ist.
2. Im Kamera-Setup die Temperaturregelung einstellen, Setpoint −30◦ C einstellen.
Dieser Wert wird u.U. nicht erreicht, eine Messung ist nur dann sinnvoll, wenn
Temperaturen unter 0◦ C erreicht werden können. Sollte dies im Sommer nicht
der Fall sein, werden Ihnen die prinzipiellen Schritte der Aufnahme erklärt. Die
nachfolgende Datenauswertung muss dann leider “aus der Konserve” erfolgen.
Warten Sie einige Minuten, bis sich die Temperatur des CCD stabilisiert hat.
Um eine CCD-Aufnahme zu erhalten, wird wie folgt vorgegangen:
1. Settings
2. Autodark aktivieren
3. Expose
4. In der Dialogbox ist die Belichtungszeit (in sec) einzugeben
Während der ersten ∼ 10 s der Belichtung muss außerdem das Licht der Vergleichslampen aufgenommen werden. Nach der Belichtung wird das Bild automatisch ausgelesen,
in den PC übertragen und dann dargestellt.
Anschließend ist das Bild zu speichern mit File-Save Filename (mit Extension FIT angeben!), um die Daten auf einen anderen Rechner transferieren zu können.
Das FITS-Format (Flexible Image Transport System) ist ein Datenformat, das sich für
CCD-Bilder in der Astronomie allgemein durchgesetzt hat. Im Vergleich zu anderen
40
Bildformaten (z.B. GIF oder Jpeg) verzichtet es auf Datenkompression und anderen
Platz sparenden “Schnickschnack”. Daher können FITS-Dateien sehr groß werden. Ein
Vorteil des FITS-Formates ist, dass es maschinenunabhängig ist und außer den reinen
Bilddaten weitere Informationen wie zum Beispiel die Beobachternamen, eine Identifikation des beobachteten Objektes, des Teleskops usw. enthält.
Für den Versuch sind die folgenden Aufnahmen zu machen:
• Eine oder mehrere Aufnahmen von Sternspektren mit gleichzeitigem Vergleichsspektrum. Die jeweilige Belichtungsdauer ist abhängig von der Himmelshelligkeit, Richtwert sind 60 bis 600 s.
• Mehrere Dunkelstromaufnahmen (“Dark Frames”). Diese sind mit gleicher Belichtungszeit wie die vorher ausgewählte Spektralaufnahme zu machen.
Flatfield-Aufnahmen entfallen an dieser Stelle, da diese bereits in der Dämmerung
von einem sternenfreien Gebiet des Himmels gemacht werden müssten, wofür im Rahmen des Praktikums ein zu kurzes Zeitfenster zur Verfügung steht.
Auswertung
Die folgenden Auswerteschritte führen Sie an einem LINUX-Rechner durch. Ihre
Aufgabe ist es, anhand der Wellenlängenliste (Tab. 8) und des in Abbildung 30 auf Seite 37 gezeigten Kalibrationsspektrums die sichtbaren Kalibrationslinien zu identifizieren und diese in Ihrem Ausdruck zu markieren. Da der Spektrograph in guter Näherung
eine lineare Dispersion hat, können Sie anschließend mit Hilfe einer linearen Regression
den Spektrographen eichen.
Die Auswertung der Aufnahmen erfolgt mit der Interpretersprache IDL (Interactive
Data Language) der Firma Research Systems, Boulder, CO, die seit September 2000
zu Kodak gehört. IDL kann sowohl in einem interaktiven Modus betrieben werden als
auch komplette Programme ausführen. Der große Vorteil von IDL liegt in der einfachen
Behandlung von Datenfeldern (Arrays), wodurch es besonders für die Bildverarbeitung
prädestiniert ist.
Starten Sie zunächst IDL durch den Befehl idl. Das Programm meldet sich mit
dem Prompt
IDL>
Laden Sie das CCD-Bild des Sternspektrums in ein Array namens image und zeigen Sie es in einem Fenster an:
IDL> image=readfits(’filename.fits’,header)
IDL> ccd_tv,image
IDL> shade_surf,image
41
Starten Sie nun die Routine show_xy, mit der Sie sich die x/y-Koordinate der aktuellen Cursorposition im Bildfenster anzeigen lassen können. Notieren Sie sich jeweils
eine y-Position für die Eichspektren und für die Ober- und Unterkante des Sternspektrums:
IDL> ccd_tv,image
IDL> show_xy
Sie verlassen die Routine show_xy durch einen Klick mit der rechten Maustaste
in das Bildfenster. Speichern Sie die notierten Werte in Variablen. Achten Sie bei den
Variablen für das Sternspektrum darauf, welche Variable den kleineren, welche den höheren Wert enthält - dies spielt beim nächsten Schritt eine Rolle. Hier ein Beispiel mit
den Variablen yeich und yspek:
IDL>
IDL>
IDL>
IDL>
yeich1
yeich2
yspek1
yspek2
=
=
=
=
396
112
230
250
Kopieren Sie jeweils eine Zeile aus dem Bild, um den Intensitätsverlauf im Eichspektrum und im Sternspektrum in einem Array zu speichern. Erläuterung: Sie greifen
auf das zweidimensionale Array image zu mit dem x-Index * = alle Elemente und dem
zuvor gespeicherten y-Index. Die Arrays eicharr und spekarr enthalten nun den
jeweiligen Intensitätsverlauf:
IDL>
IDL>
IDL>
IDL>
eicharr1 = image[*,yeich1]
eicharr2 = image[*,yeich2]
spekarr = image[*,yspek1]*1.0
for k=1,yspek2-yspek1+1 do
spekarr = spekarr + image[*,yspek1+k]*1.0
IDL> spekarr = spekarr / (yspek2-yspek1+1)
Plotten Sie den Inhalt der Arrays in einem Bildschirmfenster. Hinweis: Mit /ylog
wählen Sie eine logarithmische Darstellung, mit ystyle=1 weisen Sie IDL an, die
y-Grenzen der Grafik auf die tatsächlichen Minimum- und Maximum-Werte zu setzen.
IDL> plot,eicharr1,/ylog,ystyle=1
IDL> oplot,eicharr2
IDL> plot,spekarr,ystyle=1
Erzeugen Sie nun einen Ausdruck von diesen Plots. Auf den Ausdrucken sollten
die Achsen beschriftet sein und der Plot einen Titel haben. Der Ausdruck wird auf
Postscript-Druckern erfolgen. Dazu ist der Plot in eine Datei (hier eichplot.ps)
zu schreiben, welche anschließend auf dem Drucker ausgegeben wird (lange Zeilen geben Sie über den Rand hinaus ein, es erfolgt automatisch ein Umbruch in die nächste
Zeile):
42
IDL> open_print,’eichplot.ps’,/postscript
IDL> plot,eicharr1,/ylog,ystyle=1,title="Eichspektrum",
ytitle="Intensitaet",xtitle="Pixelnummer"
IDL> close_print,/ghost
Nach dem letzten Befehl erscheint das Programm Ghostview, welches die Datei
eichplot.ps auf dem Bildschirm darstellt. Über den Menüpunkt “File/Print...” kann
die Datei auf dem angegebenen Drucker ausgedruckt werden, eventuell ist der Druckername zuvor zu ändern.
Plotten Sie nun das Eichspektrum noch einmal auf dem Bildschirm (mit den Pfeiltasten lassen sich vorherige Befehle nochmals aufrufen), und rufen Sie die Routine
show_xy auf, um die x-Positionen der Spektrallinien der Eichlampen zu bestimmen.
Notieren Sie diese auf Ihrem Ausdruck.
IDL> plot,eicharr1,/ylog,ystyle=1,title="Eichspektrum",
ytitle="Intensitaet",xtitle="Pixelnummer"
IDL> show_xy
Bestimmen sie mit Hilfe einer Cross-Correlation (c_correlate) die Verschiebung
zwischen den beiden Eichspektren. Wie groß ist die Verschiebung, die Sie für das Sternspektrum berücksichtigen müssen? indgen(41)-20 erzeugt dabei ein Feld, belegt
mit Integerwerten von -20 bis +20. Der x-Wert des Peaks gibt die Verschiebung an.
Falls Sie das Gefühl haben, die Verschiebung ist mehr als nur 20 Pixel, ändern sie die
Grenzen des indgen(41)-20-Befehls entsprechend ab.
IDL> shift = indgen(41)-20
IDL> fit = c_correlate(eicharr1,eicharr2,shift)
IDL> plot,shift,fit
Anschließend versuchen Sie, diese Linien durch Vergleich mit dem Eichspektrum
(Abb. 30) zu identifizieren. Beachten Sie, dass die Linienintensitäten nicht unbedingt
im gleichen Verhältnis zu stehen brauchen wie in der Vorlage, wichtig ist das Verhältnis
der Linienabstände!
Notieren Sie sich zu jeder identifizierten Linie die Wellenlänge. Tragen Sie Ihre
gemessenen Pixelnummern und die Wellenlängen der identifizierten Linien in jeweils
ein Array ein. Addieren sie die Verschiebung des Sternspektrums bzgl. der Eichspektren
auf pixarr auf. Beispiel: Pixelwerte in pixarr und Wellenlängenwerte in wvlarr:
IDL> pixarr=[7,26,76,122,186,231,249,345,371,432,506,542]
IDL> pixarr = pixarr + Verschiebung
IDL> wvlarr=[6143,6164,6217,6266,6334,6383,6402,6506,6532,
6599,6678,6717]
Plotten Sie Pixel gegen Wellenlänge. Wenn Ihre Identifizierung richtig war, sollte
sich eine Gerade ergeben:
43
IDL> plot,pixarr,wvlarr,ystyle=1,psym=2
Sollte sich keine Gerade ergeben, so überprüfen Sie zunächst, ob Sie in beide Arrays
gleich viele Werte eingetragen haben. Sie können die Einträge korrigieren, indem Sie
den betreffenden Befehl mit den Pfeiltasten wieder aufrufen, und dann editieren. Wenn
kein Tippfehler vorliegt, ist vermutlich die Identifizierung falsch. Versuchen Sie, eine
bessere Identifizierung zu finden und korrigieren Sie Ihre Werte, bis sich eine Gerade
ergibt. Drucken Sie Ihre Eichkurve zur Dokumentation wieder aus:
IDL> open_print,"eichgerade.ps",/postscript
IDL> plot,pixarr,wvlarr,ystyle=1,title="Eichgerade",
ytitle="Wellenlaenge (A)",xtitle="Pixelnummer",psym=2
IDL> close_print,/ghost
Zur Bestimmung der Geradengleichung führen Sie eine lineare Regression durch.
Dies erledigt die IDL-Funktion poly_fit. Sie führt eine Polynom-Anpassung an die
Wertepaare durch, der Grad des Polynoms ist als Parameter zu übergeben. Für eine Gerade ist der Grad 1. Rückgabewert der Funktion ist ein Array (hier a) mit den PolynomParametern:
IDL> a=poly_fit(pixarr,wvlarr,1)
Lassen Sie sich die Parameter anzeigen:
IDL> print,a
Die erste angezeigte Zahl ist der y-Achsen-Abschnitt der Eichgeraden, also die Wellenlänge für Pixel 0. Die zweite Zahl ist die Steigung der Geraden, also der Eichfaktor
in Å/Pixel.
Nun ist das Sternspektrum mit einer Wellenlängeneichung zu versehen. Dazu müssen Sie zunächst die Größe des Arrays mit dem Sternspektrum wissen:
IDL> help,spekarr
SPEKARR
FLOAT
= Array[765]
Die zweite Zeile ist die Ausgabe des help-Befehls. In diesem Fall handelt es sich
also um ein Array mit 765 Werten. Erzeugen Sie nun ein Array mit den Pixelwerten von
0 bis 764 (findgen(765)) und wenden Sie darauf die Geradengleichung mit den
gefundenen Eichparametern an:
IDL> lambda=a[0]+a[1]*findgen(765)
Das Ergebnis ist ein Array mit den Wellenlängenwerten (hier lambda) zu jedem Pixelwert des Sternspektrums.
44
IDL> open_print,"eichgerade.ps",/postscript
IDL> plot,pixarr,wvlarr,ystyle=1,title="Eichgerade",
ytitle="Wellenlaenge (A)",xtitle="Pixelnummer",psym=2
IDL> oplot,findgen(765),lambda
IDL> close_print,/ghost
Plotten Sie Ihr Sternspektrum mit Wellenlängenskala zunächst auf dem Bildschirm
und drucken Sie es anschließend aus. Drucken Sie auch das Eichlampenspektrum mit
Wellenlängeneichung aus:
IDL> open_print,"sternspektrum.ps",/postscript
IDL> plot,lambda,spekarr,ystyle=1,title="Sternspektrum",
ytitle="Intensitaet",xtitle="Wellenlaenge (A)"
IDL> close_print,/ghost
IDL> open_print,"eichspektrum.ps",/postscript
IDL> plot,lambda,eicharr1,ystyle=1,/ylog,title="Eichspektrum",
ytitle="Intensitaet",xtitle="Wellenlaenge (A)"
IDL> close_print,/ghost
Rufen Sie wieder die Routine show_xy auf und bestimmen Sie die Wellenlängen
der Absorptionslinien:
IDL> plot,lambda,spekarr,ystyle=1,title="Sternspektrum",
ytitle="Intensitaet",xtitle="Wellenlaenge (A)"
IDL> show_xy
Identifizieren Sie die wichtigsten Linien anhand Anhang C. Zusätzlich können Sie
die NIST Atomic Spectral Database zu Hilfe nehmen (http://physics.nist.
gov/PhysRefData/ASD/lines_form.html). Sollte show_xy keine Koordinaten anzeigen, identifizieren Sie sie von Hand mit Hilfe der Ausdrucke. Vergleichen Sie
die gemessene Wellenlänge mit der tabellierten Wellenlänge. Falls dort eine Differenz
von mehr als 1 Å auftritt, kann es sein, daß die CCD-Kamera nicht völlig parallel zum
Spektrum ausgerichtet war. Sie werden dann im CCD-Bild eine Differenz der Pixelpositionen für einzelne Spektrallinien im oberen und unteren Eichspektrum feststellen.
Etwa die Hälfte dieser Differenz ergibt sich damit als Abweichung zwischen Eichspektrum und Sternspektrum. Berücksichtigen Sie diesen Offset bei der Identifizierung der
übrigen Linien.
Tip: Sie können auch mit dem Cursor alle in der Tabelle angegebenen Linienpositionen anfahren und nachsehen, ob sich dort im Sternspektrum eine Absorption befindet.
Aufgabe 10: Stellen Sie anhand Ihrer Ausdrucke dar, wie die Aufnahmen reduziert und wellenlängenkalibriert wurden. Welcher ist der Spektraltyp des aufgenommenen Sterns?
Aufgabe 11: Was ist physikalisch der qualitative Unterschied des Spektrums der Vergleichslampen und dem der Sterne? Warum sehen Sie also im Spektrum der Sterne Absorptionslinien, in dem der Vergleichslampen Emissionslinien? Was für Informationen können aus den aufgenommenen Sternspektren gewonnen werden?
45
Abschließend vergleichen Sie die beobachteten Spektren mit einem Sonnenspektrum vom NOAO. Erstellen Sie in gewohnter Weise einen Ausdruck mit Achsbeschriftung, markieren und identifizieren Sie die signifikantesten Spektrallinien. Hierzu ist es
von Vorteil, den dargestellten Plotbereich mittels xrange=[3500,4500] schrittweise abzutasten.
IDL> .r read_solspec
Das Sonnenspektrum können sie mit einer Gaussfunktion glätten:
IDL> smoothed_flux=gaussfold(WAVE_SOL,FLUX_SOL,6)
IDL> plot,WAVE_SOL,smoothed_flux
4.3
Photometrie eines Sternhaufens
Die Photometrie wird ebenfalls mit unserem 0,8 m-Reflektor durchgeführt. Die Inbetriebnahme wird an Ort und Stelle erklärt. Zur Datenaufnahme verwenden wir eine
STL-1001E-Kamera, deren Bedienung nahezu identisch zu der bei der Spektroskopie
verwendeten ist. Ein Unterschied ist ein Filterrad (Tab. 6), in dem verschiedene Filter
untergebracht sind. Die Ansteuerung des Filterrads geschieht über das Steuerprogramm
MaximDL.
Tabelle 6: Filterbestückung der STL-1001E Kamera.
Filter
Bandbreite [Å]
Rot (R)
5800 - 6800
Grün (V)
4500 - 5800
Blau (B)
3900 - 5000
Luminance (L) 4000 - 6800
Clear (C)
3000 - 10000
Eine Verbesserung des Ergebnisses der Photometrie würden Flatfield-Aufnahmen
ermöglichen, die für alle verwendeten Filter in der Dämmerung aufgenommen werden.
Wie auch bei der Spektroskopie, entfällt dieser Schritt in der Beobachtungsnacht aus
zeitlichen Gründen.
Das Teleskop wird nun auf einen offenen Sternhaufen ausgerichtet und dieser photometriert.
Aufgabe 12: Nehmen Sie den Sternhaufen in den Filtern B und V auf. Mehrere kürzere Aufnahmen sind besser als eine lange. Aktivieren Sie bei den Aufnahmen die AutodarkFunktion, um eine automatische Darkkorrektur vorzunehmen. Notieren Sie sich am besten auch gleich die Belichtungsdauer.
46
Auswertung
Zur Auswertung werden wir wieder IDL verwenden. Mit Hilfe des Programms
MakeFHD erfolgt die Auswertung automatisch. Folgen Sie den vom Programm vorgegebenen Schritten, achten Sie also auf Bildschirmmeldungen.
IDL> .r MakeFHD
Zuerst werden die mit verschiedenen Filtern aufgenommenen Bilder eingelesen und
Flatfield-korrigiert. Nun müssen die Helligkeiten in den verschiedenen Filtern an die
Helligkeiten der Standartfilter angepasst werden. Dazu markiert man mehrere Sterne,
die man in der Literatur (z.B. SIMBAD, Webda) identifizieren kann und vergleicht die
Helligkeitsangaben in B und V aus der Literatur mit denen der Aufnahmen. Anschließend gibt man fuer B und V Korrekturwerte an.
Sternkataloge:
• SIMBAD (http://simbad.u-strasbg.fr/Simbad)
• Webda (http://www.univie.ac.at/webda/navigation.html)
Hier eine kleine Anleitung für den Umgang mit Webda:
1. Display the Page of the Cluster: Name des Clusters eintragen
2. cluster chart
3. chart form
4. Achsen anpassen (eventuell auch die maximale Helligkeit)
5. Sterne auswählen, B und V notieren
6. Grafik für das Protokoll ausdrucken
Der nächste Schritt besteht darin, die einzelnen Aufnahmen exakt aufeinander auszurichten. Hierzu ist es notwendig, auf den einzelnen Bildern jeweils denselben Referenzstern zu markieren.
Jetzt werden die Haufen-Sterne auf einem Bild von Hand identifiziert und ihre Helligkeiten auf allen Bildern automatisch bestimmt. Sterne nahe am Rand werden dabei
von der Software ignoriert. Die (B-V)-Helligkeiten der Sterne werden berechnet und
ein Farben-Helligkeits-Diagramm erzeugt. Die interstellare Extinktion muss der Literatur entnommen und angegeben werden.
Um den Abstand des Sternhaufens von der Erde zu berechnen, muss der Entfernungsmodul V −Mv bestimmt werden. Aus den erzeugten Postscript-Plots des FHD und
47
der ZAMS (Alter-Null-Hauptreihe) bestimmt man per Augenmaß einen ersten Schätzwert für V − Mv , gibt ihn an und optimiert ihn iterativ derart, dass sich das FHD der
Sterne an die ZAMS anschmiegt.
Um das Alter des Sternhaufens zu berechnen, bestimmt man die absolute Helligkeit der hellsten Sterne des FHD, die sich gerade noch auf der Hauptreihe befinden.
Die zweite Methode besteht darin, wiederum iterativ das FHD des Sternhaufens mit
berechneten Isochronen in Übereinstimmung zu bringen.
Aufgabe 13: Was erkennt man im Plot des FHD ?
Wie groß sind Entfernung und Alter des Sternhaufens ?
Vergleichen Sie Ihre Ergebnisse mit Literaturwerten und diskutieren Sie eventuelle Abweichungen.
Damit sind wir mit der Photometrie fertig.
48
5
Literatur
Born M., Wolf E., 1980, Principles of Optics,
Pergamon, Oxford, New York, 6th edition
Bronstein I.N., Semendjajew K.A., 1987, Taschenbuch der Mathematik, Harri Deutsch
Karttunen H., Kröger P., Oja H., et al., 1990,
Astronomie, Springer, Berlin, Heidelberg
Kitchin C.R., 1984, Astrophysical Techniques,
Adam Hilger, Bristol, Philadelphia, 1st edition
McLean I.S., 1997, Electronic Imaging in
Astronomy, Wiley-Praxis, Chichester, New
York
Newton I., 1730, Opticks, Vol. 4th, William
Innys, London reprint: Dover Publications,
1952
Optomechanics Research 1997, Model 10 C
Cassegrain Spectrograph, Tucson
Schmidt W., 1995, Optische Spektroskopie,
VCH, Weinheim
Seeds M., 1997, Foundations of Astronomy,
Wadsworth Publishing Company, 4. edition
Staudt G., 1993, Experimentalphysik II, Attempto, Tübingen 2. Auflage
Unsöld A., Baschek B., 1988, Der Neue Kosmos, Springer Verlag, 4. edition
Weigert A., Zimmermann H., 1976, Brockhaus
ABC der Astronomie, VEB F.A. Brockhaus,
7. edition
49
A
Mögliche Beobachtungsobjekte
Tabelle 7: Verzeichnis von Beobachtungsobjekten.
Name
M11
M29
M35
M36
M37
M38
M52
NGC 6819
α Aql
α Aur
α Cyg
β Cyg
β Gem
α Lyr
α Ori
η UMa
Typ
offener Haufen
offener Haufen
offener Haufen
offener Haufen
offener Haufen
offener Haufen
offener Haufen
offener Haufen
Stern
Stern
Stern
Stern
Stern
Stern
Stern
Stern
50
B
Wellenlängenkalibration
Tabelle 8: Laborwellenlängen der Hg- und Ne-Kalibrationslampen nach Kurucz
(http://cfa-www.harvard.edu/amdata/ampdata/kurucz23/sekur.
html).
Ion
Hg I
Hg I
Ne I
Hg I
Hg I
Ne I
Ne I
Ne I
Ne I
Hg I
Hg I
λ [Å]
4046.559
4077.827
4314.252
4358.323
4916.062
5116.503
5330.777
5341.094
5400.562
5460.731
5769.593
Ion
Hg I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
λ [Å]
5790.660
5852.488
5881.895
5944.834
5975.534
6029.997
6074.338
6096.163
6143.062
6163.594
6217.281
51
Ion
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
Ne I
λ [Å]
6266.495
6304.789
6334.428
6382.991
6402.246
6506.528
6532.882
6598.953
6678.331
6717.043
C
Starke Linien in Sternspektren.
Wasserstoff
Hα
Hβ
Hγ
Hδ
Hε
Hζ
Hη
Hθ
6563 Å 4861 Å 4340 Å 4102 Å 3970 Å 3889 Å 3835 Å 3798 Å
Hι
Hκ
H13
H14
H15
H16
H17
H18
3771 Å 3750 Å 3734 Å 3722 Å 3712 Å 3704 Å 3697 Å 3692 Å
Helium
He I
He I
He II
He II
3820 Å
4387 Å
3923 Å
4686 Å
3965 Å
4471 Å
4100 Å
4861 Å
4009 Å 4026 Å 4144 Å
5876 Å
4199 Å 4340 Å 4542 Å
5411 Å 6678 Å
Kohlenstoff
C II
4267 Å
C III 4069 Å 4123 Å 4187 Å 4340 Å 4375 Å 4515 Å 4650 Å
C IV 4441 Å 4650 Å 4786 Å
Stickstoff
N II
3995 Å 5005 Å 5679 Å
N III 4100 Å 4640 Å
N IV 4057 Å
52
Sauerstoff
OI
6158 Å
O II
3749 Å 4119 Å 4317 Å 4320 Å 4349 Å 4415 Å 4417 Å 4649 Å
O III 3444 Å 3760 Å 4069 Å
O IV 4786 Å
O V 4123 Å 4157 Å 4187 Å
Natrium
Na I 5890 Å 5896 Å
Silizium
Si II
4128 Å 4130 Å
Si III 4552 Å
Si IV 4089 Å
Calcium
Ca I
4227 Å 4289 Å 4303 Å 4435 Å 4455 Å 5016 Å 5262 Å
Ca I 5270 Å 5589 Å 5857 Å 6122 Å 6439 Å 6718 Å
Ca II 3934 Å 3968 Å
53
Eisen
Fe I
3930 Å 4005 Å 4045 Å 4064 Å 4144 Å 4250 Å 4260 Å 4272 Å
Fe I
4325 Å 4384 Å 4405 Å 4528 Å 4668 Å 4891 Å 4958 Å 5255 Å
Fe I 5269 Å 5616 Å 6609 Å 6663 Å 6678 Å
Fe II 3914 Å 3938 Å 3945 Å 4179 Å 4233 Å 4385 Å
verschiedene Metalle
Mg I
Mg II
Sc II
Ti I
Ti I
Ti II
3838 Å
4481 Å
4247 Å
4523 Å
4640 Å
4164 Å
5167 Å 5173 Å 5184 Å
Cr I
Cr II
Mn I
Sr II
Sr III
Eu II
4254 Å 4646 Å 4651 Å
4242 Å
3807 Å 4031 Å 4033 Å 4034 Å 4041 Å
4077 Å 4215 Å 4305 Å
4335 Å
4205 Å
4527 Å 4533 Å 4545 Å 4617 Å
4982 Å 5036 Å 6258 Å
4300 Å 4395 Å 4400 Å 4408 Å 4444 Å 4468 Å
54
Moleküle
CH
CN
CN
4300 Å 3883 Å 4216 Å
TiO
TiO
TiO
TiO
TiO
TiO
4585 Å 4761 Å 4954 Å 5000 Å 5167 Å 6159 Å
Emissionslinien in Gasnebeln
[O I]
[O I]
[O I]
[O I]
[O II]
5007 Å 5577 Å 6300 Å 6363 Å 3727 Å
[O III]
[O III]
[O III]
[O III]
4363 Å 4391 Å 4959 Å 5007 Å
[Ne III]
[S II] [Fe III]
[N I] [Cl III] [Cl III]
[N II]
[S II]
3868 Å 4069 Å 4658 Å 5200 Å 5517 Å 5537 Å 5754 Å 6723 Å
Erdatmosphäre
O2
O2
O2
O2
O2
H2 O
6280 Å 6867 Å 6875 Å 6906 Å 7594 Å 7165 Å
55
D
Aufbau des Versuchsprotokolls
1. Ziel und Inhalt des Experiments
• Was soll gezeigt bzw. herausgefunden werden ?
• Was ist der größere Kontext ?
2. Material, Methoden, Durchführung
• verwendetes Material (Teleskop, Kamera, Spektrograph) genau
erläutern
• genaue, detaillierte Experimentbeschreibung
• Skizzen des Aufbaus und Ablaufs, falls erforderlich
• evtl. Probleme und ihre Lösungen schildern
3. Darstellung der Ergebnisse
• Messwertetabelle (z.B. Helligkeiten der Referenzsterne) mit genauer Erläuterung
• graphische Darstellungen mit Beschriftung
• durchgeführte Berechnungen, verwendete Gleichungen (z.B. Entfernungsmodul)
• Aufgaben aus der Anleitung mit Aufgabenstellung und detaillierter Lösung inkl. Lösungsweg
4. Interpretation und Diskussion
• Wurde das gesetzte Ziel erreicht ?
• Was sagt uns das Ergebnis, was kann man daraus lernen ?
• Muss das Experiment verändert werden, um das Ziel zu erreichen ?
• gegebenenfalls Abweichung des Ergebnisses von Literaturwerten diskutieren
56
57
Welt der Wissenschaft: GroSSteleskope
Eine Frage
der Ehre
Der Wettstreit um den weltgrößten Refraktor
Im 19. Jahrhundert entbrannte ein Wettstreit um das größte Linsenfernrohr der Welt.
Zwar gab es gute wissenschaftliche Gründe für leistungsstarke Teleskope, aber in vielen
Fällen ging es hauptsächlich um die nationale Ehre. Oft entschieden nur Millimeter
über den mehr oder weniger ruhmreichen Rekordhalter.
Von Wolfgang Steinicke und Stefan Binnewies
ó Nachdem in der ersten Hälfte
des 19. Jahrhunderts die Herstellung von Linsen und Objektiven
S
Refraktoren berichtet von Erfolgen, aber
Epoche der Astronomie: die gro­
auch von Fehlschlägen und Katastrophen.
ßen Refraktoren. Heute meist nur
Der Startpunkt ist 1824, das Jahr, in dem
noch Museumsstücke, gehörten
Joseph von Fraunhofer neue Maßstäbe im
sie im 19. Jahrhundert zur Standardaus­
stattung jeder bedeutenden Sternwarte.
Fernrohrbau setzte.
perfektioniert wurde, setzte ein
Zunächst für visuelle Beobachtungen
Präzision gegen Öffnung
Wettstreit um den weltgrößten
genutzt, wurden sie später auch für foto­
Ende 1824 erhielt Wilhelm Struve, der Di­
Refraktor ein.
grafische und spektroskopische Zwecke
rektor der Sternwarte Dorpat (heute Tartu
eingesetzt.
in Estland), 22 schwere Kisten aus Deutsch­
ó Neben staatlich finanzierten
Sternwarten in Europa und den
Ein großer Refraktor diente aber noch
land. Sie enthielten Fraunhofers Meister­
USA beteiligten sich auch private
einem anderen Zweck: Er sollte Ruhm und
stück: einen 24,4-Zentimeter-Refraktor
Sponsoren und Amateurastro-
Ehre bringen. So gab es einen andauernden
mit 4,1 Meter Brennweite – den größten
nomen am Bau immer größerer
Wettstreit der Nationen, Sternwarten und
der Welt. Nachdem Struve die Einzelteile
Linsenfernrohre.
Sponsoren um das weltweit größte Lin­
sorgsam zusammengefügt hatte, war das
senfernrohr. Wie im Sport entschieden oft
imposante Gerät an Heiligabend betriebs­
nur wenige Millimeter über den Sieg, und
bereit: ein edler Mahagonitubus auf einer
so mancher Rekordhalter verschwand bald
uhrwerkgetriebenen Montierung mit ge­
wieder in der Bedeutungslosigkeit.
schwungenem Holzstativ (siehe Bild auf
die
S. 46 links). Sein englischer Kollege John
Grenzen des technisch Möglichen – und
Herschel pries es als »probably the very
überschritten sie teilweise. Einige Exem­
best refracting telescope ever made«.
Die
Konstrukteure
erreichten
Zu diesem Beitrag stehen didaktische
plare erinnern eher an Kanonenrohre als
Sogleich begann Struve mit dem Ver­
Materialien auf unserer Internetseite
an Teleskope. Ihre Länge und das enorme
messen von Doppelsternen; im Jahr 1827
www.wissenschaft-schulen.de/
Gewicht von Objektiv, Tubus und Montie­
erschien ein erster Katalog. Zwischen 1835
artikel/1114673 zur Verfügung.
rung erforderten gewaltige Kuppelbauten.
und 1838 versuchte er mit dem Präzisions­
Die folgende kurze Geschichte der großen
instrument die Parallaxe des Sterns Wega
44
August 2011
Sterne und Weltraum
Stefan Binnewies
In Kürze
ie sind Zeugen einer bedeutenden
58
Der 27-Zoll-GrubbRefraktor der Wiener
Universitätssternwarte holte 1883 den Titel
des weltgrößten
Linsenteleskops von
den USA nach Europa
zurück.
www.astronomie-heute.de
August 2011
45
59
35,5-Zentimeter-Objektiv mit 7,6 Meter
Brennweite erstanden. Zwischen Coopers
Refraktor und den Instrumenten von
Fraunhofer und Merz liegen allerdings
Welten. Zunächst erhielt das Teleskop ei­
nen einfachen Holztubus auf azimutaler
Herschel-Montierung, drei Jahre später
versah der irische Optiker und Teleskop­
bauer Thomas Grubb das Gerät mit einem
Eisentubus und setzte es auf eine paral­
laktische Montierung, die auf einer vier
Meter hohen Steinpyramide ruhte (siehe
Bilder rechts oben und Mitte).
Archiv Wolfgang Steinicke
Der Refraktor stand nicht in einer
Kuppel. Vielmehr schützte ein vier Meter
hoher Mauerring das Instrument notdürf­
tig vor Wind und Wetter. Coopers größte
Leistung war die Erstellung des »Markree
Catalogue«, der über 60 000 Sterne entlang
der Ekliptik enthält. Er erschien zwischen
Der von Joseph von Fraunhofer gebaute
1851 und 1856 in vier Bänden; der zuge­
Dorpat-Refraktor ist heute ein Museums-
hörige Atlas blieb unveröffentlicht und
stück.
lagert heute im englischen Cambridge.
Das Schicksal des Markree-Refraktors
ist so seltsam wie sein Aussehen. Nach
zu ermitteln. Der erhaltene Wert war je­
Jahren des Zerfalls kam er 1902 nach
doch noch sehr ungenau. Da zur gleichen
Hongkong – und stand dort wieder im
Zeit Friedrich Wilhelm Bessel – auch mit
Regen. Im Jahr 1941 wurde das Fernrohr
einem Refraktor aus der Fraunhofer’schen
bei einem Luftangriff stark beschädigt,
Werkstatt – einen zuverlässigen Wert für
das Objektiv tat aber bis 1989 im Littrow-
die Parallaxe des Sterns 61 Cygni ermit­
Spektrografen der Sternwarte Manila sei­
telte, gilt Bessel als derjenige, der als Erster
nen Dienst.
Bereits kurz nach der Errichtung des
Transatlantische Rivalen
Dorpat-Refraktors bestellte die Münchner
Die Firma Merz, mittlerweile durch Joseph
Sternwarte bei Fraunhofer ein Gerät mit
Mahler verstärkt, konterte im Jahr 1839.
einem Objektivdurchmesser von 35,6 Zen­
Auf Anweisung von Zar Nikolaus I. hatte
timetern. Bedingt durch Fraunhofers Tod
Wilhelm Struve in Dorpat mit der Planung
im Jahr 1826 konnte der Nachfolger Georg
für ein russisches Nationalobservatorium
Merz aber nur einen 28,5-Zentimeter-Re­
in Pulkowo bei St. Petersburg begonnen.
fraktor liefern, der 1835 in Bogenhausen
Merz & Mahler lieferte dafür einen Re­
aufgestellt wurde. Im gleichen Jahr erhielt
fraktor mit 38 Zentimeter Öffnung und
die Berliner Sternwarte ein Duplikat des
6,9 Meter Brennweite (siehe Bild auf S. 48
Dorpat-Refraktors.
entdeckten
oben links). Die Sternwarte wurde im Au­
Gottfried Galle und Heinrich d’Arrest am
gust 1839 eingeweiht, Struve wurde ihr
23. September 1846 den Planeten Neptun.
ers­ter Direktor. Zentrales Arbeitsgebiet
Das historische Instrument ist heute im
war die Beobachtung von Doppelsternen,
Deutschen Museum in München zu se­
wobei sich besonders Otto Struve her­
hen. Der 28,5-Zentimeter-Merz-Refraktor
vortat, der 1862, zwei Jahre vor dem Tod
steht nach wie vor in Bogenhausen. Stru­
seines Vaters, die Leitung von Pulkowo
ves »Fraunhofer« wurde 1993 in Tartu re­
übernahm.
Damit
stauriert und kann in der alten Sternwarte
besichtigt werden.
Archiv Wolfgang Steinicke
die Entfernung eines Sterns bestimmte.
Der russische Refraktor rief einen neu­
en Konkurrenten auf den Plan: die USA.
Den Titel des weltgrößten Refrak­
Selbstbewusst wollten Astronomen der
tors übernahm derweil ein Unikum im
Neuen Welt der europäischen Übermacht
Drei Gesichter des Markree-Refraktors: auf
irischen Markree Castle. Im Jahr 1831 hat­
in der Astronomie endlich etwas entge­
einer hölzernen Herschel-Montierung
te der Schlossherr und begeisterte Ama­
gensetzen. Eine erste Antwort war der
(oben), parallaktisch montiert mit volumi-
teurastronom Edward Cooper von dem
1845 in Cincinnati aufgestellte 30,5-Zenti­
nösem Steinsockel (Mitte) und in neuem
Pariser Optiker Robert-Aglae Cauchoix ein
meter-Refraktor von Merz & Mahler. Als
Gewand in Hongkong (unten)
46
August 2011
Sterne und Weltraum
60
Die wichtigsten Refraktoren, geordnet nach dem Jahr der Inbetriebnahme
Standort
Sternwarte / Instrument
Dorpat
Sternwarte Dorpat
Land
Jahr
Konstruktion
Durchmesser D Brennweite f
in Zentimetern in Metern
f/D
Höhe in
Metern
67
EST
1824*
Fraunhofer
24,4
4,1
16,8
Markree Castle Privatsternwarte Cooper
IRL
1831*
Cauchoix/Grubb
35,5
7,6
21,5
45
Berlin
D
1835
Merz
24,4
4,3
17,6
47
Berliner Sternwarte
München
Sternwarte Bogenhausen
D
1835
Merz
28,5
4,9
17,2
500
St. Petersburg
Sternwarte Pulkowo
RUS
1839*
Merz & Mahler
38,0
6,9
18,2
75
Cincinnati
University Observatory
USA
1845
Merz & Mahler
30,5
5,3
17,4
247
Cambridge
Harvard College Obs.
USA
1847*
Merz & Söhne
38,1
6,8
17,9
24
Wandsworth
Craig-Refraktor
UK
1852*
Chance/Gravatt
61,0
23,2
38,0
10
Paris
Porro-Refraktor
F
1856
Porro
52,0
15,0
28,8
60
Walworth
Buckingham-Refraktor
UK
1862
Buckingham/Wray
54,0
8,7
16,1
10
Chicago
Dearborn Observatory
USA
1863
Clark
47,0
8,2
17,4
175
Dunsink
South Equatorial
IRL
1868
Cauchoix/Grubb
29,8
5,8
19,5
91
Gateshead
Privatsternwarte Newall
UK
1868*
Cooke
62,5
9,1
14,6
20
Bothkamp
Privatsternwarte v. Bülow
D
1870
Schröder
29,3
4,9
16,7
32
Washington
U.S. Naval Observatory
USA
1873*
Clark
65,5
9,9
15,1
38
Potsdam
Astrophysikalisches Obs.
D
1878
Schröder
29,8
5,2
17,4
100
Dresden
Privatsternwarte
v. Engelhardt
D
1879
Grubb
30,6
3,9
12,6
124
Straßburg
Universitätssternwarte
D (F)
1880
Merz & Söhne / Repsold
48,7
6,9
14,2
144
Princeton
Halsted Observatory
USA
1882
Clark
58,0
9,8
16,9
75
Wien
Universitätssternwarte
Ö
1883*
Grubb
68,6
10,5
15,3
240
St. Petersburg
Sternwarte Pulkowo
RUS
1884*
Clark/Repsold
76,2
13,7
18,0
75
Charlottesville
Leander McCormick Obs.
USA
1885
Clark
66,8
9,9
14,9
259
Nizza
(Mont Gros)
Sternwarte Bischoffsheim
F
1887*
Henry/Gautier
76,9
17,9
23,3
376
USA
Mt. Hamilton
Lick Observatory
1888*
Clark
91,4
17,4
19,0
1283
Meudon
Observatoire de Paris-Meudon F
1891
Henry/Gautier
83,0
16,2
19,5
162
Greenwich
Royal Observatory
UK
1893
Grubb
71,1
8,5
12,0
47
Berlin-Treptow Archenhold-Sternwarte
D
1896
Steinheil/Hoppe
68,0
21,0
30,9
41
William Bay
Yerkes Observatory
USA
1897*
Clark / Warner & Swasey
102,0
19,4
19,0
334
Potsdam
Astrophysikalisches Obs.
D
1899
Steinheil/Repsold
80,0
12,2
15,3
95
Paris
Teleskop der Weltausstellung
F
1900*
Mantois/Gautier
125,0
57,0
45,6
65
Hamburg
Sternwarte Bergedorf
D
1912
Steinheil/Repsold
60,0
9,0
15,0
50
Pittsburgh
Allegheny Observatory
USA
1914
Brashear
76,2
14,4
18,9
370
Potsdam
Sternwarte Babelsberg
D
1915
Zeiss
65,0
10,1
15,5
35
Johannesburg
Yale Observatory
SA
1925
Grubb
66,0
10,6
16,1
1760
Llano del Hato
Obs. Astronómico Nacional
VEN
1972
Zeiss
65,0
10,5
16,2
3600
Hida
Hida Observatory
J
1972
Zeiss
65,0
10,5
16,2
1275
La Palma
Swedish Solar Telescope (SST)
S (SP)
2002
Svenska Bearing
97,0
20,6
21,2
2400
* bedeutet neuer Öffnungsrekord
Nächstes wollte man Pulkowo übertref­
meten Donati 1858 sowie des Orion- und
fen. William Bond, der Direktor des Har­
Andromedanebels erregten Aufsehen.
Schon zwölf Jahre später übertrumpfte
der schottische Ingenieur und Astronom
vard College Observatory in Cambridge,
Im August 1852 stellte John Craig in
Robert Newall Craigs Refraktor. In Gates­
Massachusetts, bestellte also in München
Wandsworth bei London einen neuen
head bei Newcastle errichtete er 1868 einen
bei Merz & Söhne einen Refraktor mit
Rekord auf. Gegenüber Pulkowo und Har­
neuen Rekordhalter (siehe Bild auf S. 48
38,1 Zentimeter Öffnung – ein Millimeter
vard steigerte er die Öffnung um 60 Pro­
unten Mitte). Das parallaktisch montierte
mehr als in Dorpat!
zent. Der Glashersteller Robert Chance in
Gerät, gebaut von Thomas Cooke & Sons
Das Gerät, das heute noch in Harvard
Birmingham fertigte das 61-Zentimeter-
in York, besitzt ein 62,5-Zentimeter-Ob­
zu sehen ist, leistete große Dienste bei
Objektiv; der zigarrenförmige Metalltubus
jektiv mit 9,1 Meter Brennweite. Das neun
der Beobachtung von Kometen, Planeten,
und die bizarre Turmmontierung sind das
Tonnen schwere Instrument war auf einer
Sternen und Nebelflecken (siehe Bild auf
Werk des Ingenieurs William Gravatt (sie­
5,8 Meter hohen Säule montiert. Wegen
S. 48 oben rechts). Besonderen Ruhm ern­
he Bild auf S. 48 unten links). Mechanische
der großen Luftverschmutzung und dem
teten William Bond und sein Sohn George
Probleme und fehlerhaft korrigierte Lin­
miserablen Wetter gelangen Newall nur
für die Entdeckung des Saturnmonds
sen führten jedoch dazu, dass der Refrak­
wenige Beobachtungen. Im Jahr 1891 kam
Hyperion. Auch die Zeichnungen des Ko­
tor bereits 1856 wieder abgebaut wurde.
der 25-Zöller nach Cambridge und tat dort
www.astronomie-heute.de
August 2011
47
Alle Bilder dieser Seite: Archiv Wolfgang Steinicke
61
Ein 38-Zentimeter-Refraktor, von Merz & Mahler in München
hergestellt, wurde 1839 das Hauptinstrument der neuen russischen Nationalsternwarte in Pulkowo.
Mit einem Duplikat des Pulkowo-Refraktors wollten Astronomen
am Harvard College Observatory an die Erfolge ihrer europäischen
Kollegen anknüpfen.
John Craig ließ 1852 in der Nähe von
Der 25-Zoll-Refraktor von Robert Newall,
Mit dem 26-Zoll-Refraktor des U.S. Naval
London ein monströses Turm­teleskop mit
1868 in Gateshead (England) errichtet,
Observatory in Washington entdeckte
einem 61-Zentimeter-Objektiv erbauen.
steht seit 1960 in Penteli, Griechenland.
Asaph Hall 1877 die beiden Marsmonde.
seinen Dienst bei der Beobachtung von
Erst 1893 erhielten die Briten einen grö­
deutsche V 1 beschädigt wurde. Danach
Doppelsternen, bis er in den 1950er Jahren
ßeren Refraktor: das wiederum von Grubb
verlegte man den 28-Zöller nach Herst­
ausgemustert wurde. Der Newall-Refraktor
gebaute Instrument im Royal Greenwich
monceux Castle, später der Sitz des Royal
wurde dann dem Athener Observatorium
Observatory mit 71,1 Zentimeter Öffnung
Greenwich Observatory. Im Jahr 1971 zog
geschenkt und steht seit 1960 in Penteli,
und 8,5 Meter Brennweite. Es besaß eine
er zusammen mit dem gesamten Obser­
nordöstlich von Athen. Seit 1995 ist das
eigenwillige englische Rahmenmontie­
vatorium nach Greenwich um, wo er heu­
betagte Instrument ein Museumsstück,
rung und war in einer zwiebelförmigen
te eine der Hauptattraktionen des Royal
das viele Besucher anlockt.
Kuppel untergebracht, die 1944 durch eine
Observatory ist.
48
August 2011
Sterne und Weltraum
62
Am Harvard College Observatory in
Cambridge war der große Refraktor von
Merz & Mahler unterdessen in die Jahre
gekommen, und die Amerikaner wollten
den Titel unbedingt zurückgewinnen. Mit
Alvan Clark hatten sie nun auch selbst ei­
nen hervorragenden Teleskopbauer. Seine
Firma in Cambridgeport, Massachusetts,
sollte für den Rest des Jahrhunderts den
Markt dominieren.
Im Jahr 1873 lieferte er dem U. S. Naval
Observatory in Washington den neuen Re­
kordhalter: einen Refraktor mit 65,5-Zenti­
Stefan Binnewies
meter-Objektiv und 9,9 Meter Brennweite
(siehe Bild auf S. 48 unten rechts). Vier Jah­
re später machte dieses Gerät Schlagzei­
len, als Asaph Hall damit die Marsmonde
Phobos und Dei­mos entdeckte. Das her­
vorragende Teleskop wurde hauptsächlich
Ein schlanker Riese: der 76,9-Zentimeter-Refraktor der Sternwarte Nizza mit
zur Positionsbestimmung von Planeten,
17,9 Meter Brennweite. Die Optik stammt von den Brüdern Henry.
Monden und Doppelsternen benutzt. Das
Gerät ist heute noch intakt.
Nicht nur der Neid der Europäer hielt
die Entwicklung in Gang, auch die inner­
amerikanische Konkurrenz schlief nicht.
Dies führte zum Bau eines weiteren
Clark-Refraktors, der den 26-Zöller des
U. S. Naval Observatory um 1,3 Zentimeter
übertreffen sollte. Bereits 1870 hatte der
Chicagoer Industrielle Leander McCor­
mick die Idee, den weltgrößten Refraktor
aufzustellen. Doch es vergingen noch
einige Jahre, bis er der University of Vir­
ginia in Charlottesville Mittel für eine
Sternwarte zur Verfügung stellte. Der Bau
verzögerte sich durch allerlei Probleme,
so dass schon vor dessen Vollendung ein
58-Zentimeter-Refraktor am Halsted Ob­
servatory, Prince­ton, in Betrieb ging. Doch
damit nicht genug: Als McCormicks Gerät
auf dem 260 Meter hohen Mt. Jefferson im
April 1885 endlich erstes Licht sah, waren
in Wien und Pulkowo bereits zwei größere
Instrumente in Betrieb gegangen.
Der europäische Dreikampf
Wien hatte den Titel des weltgrößten Re­
fraktors durch einen von Grubb gebauten
27-Zöller mit 10,5 Meter Brennweite 1883
nach Europa zurückgeholt. Der 68,6-Zen­
timeter-Refraktor thront seitdem in einer
Stefan Binnewies
14-Meter-Kuppel auf dem mächtigen Ge­
bäude der Universitätssternwarte an der
Türkenschanze (siehe Bild auf S. 45).
Die Freude in Wien währte indes nur
eineinhalb Jahre, dann gab es einen neu­
en Spitzenreiter. Otto Struve hatte für die
Der 36-Zoll-Refraktor des Lick Observatory wurde mit privaten Mitteln
Sternwarte in Pulkowo bei Alvan Clark &
erbaut. Erst 1888, zwölf Jahre nach dem Tod des Stifters James Lick, wurde
Sons einen imposanten 76,2-Zentimeter-
der Bau der Sternwarte auf dem Mt. Hamilton in Kalifornien vollendet.
www.astronomie-heute.de
August 2011
49
63
Nach wie vor der Rekordhalter: der
Yerkes-Refraktor mit 1,02 Meter Öffnung.
Die Brennweite beträgt 19,8 Meter, die
beweglichen Teile wiegen 20 Tonnen.
Refraktor mit 13,7 Meter Brennweite in
Auftrag gegeben. Im Jahr 1884 ging das
Gerät in einem zylinderförmigen Schutz­
bau in Betrieb. Die Montierung stammte
von der Hamburger Firma Repsold. Der
alte »Merz« musste nun weichen und wur­
de (ohne Objektiv) verkauft. Das Fernrohr
stand später im Deutschen Museum in
München, bis es dort Ende 1944 durch alli­
ierte Bomber zerstört wurde. Noch schlim­
mer erging es der Sternwarte Pulkowo: Sie
wurde 1942/43 während der deutschen
Belagerung von Leningrad verwüstet.
Im Jahr 1887 machte ein neuer Standort
von sich reden: der 360 Meter hohe Mont
Gros nahe Nizza. Das Observatorium war
ein Geschenk des Industriellen Raphaël
Bischoffsheim. Auch er träumte vom welt­
größten Refraktor. Diesmal gelang das Vor­
haben: Mit dem 76,9 Zentimeter-Objektiv
Stefan Binnewies
der Brüder Paul und Prosper Henry wurde
Pulkowo um 7 Millimeter geschlagen
(siehe Bild S. 49 oben). Nizza lag auch mit
einer Brennweite von 17,9 Metern vorn,
und die von Gustave Eiffel konstruierte
Kuppel übertraf mit 26 Meter Durchmes­
ser und 95 Tonnen Masse alles bisher da
Gewesene. Sie war nicht wie sonst üblich
auf Rollen gelagert, sondern schwamm in
einer kreisförmigen Wanne. Mittlerweile
ist das Instrument mitsamt dem neo­
klassizistischen Gebäude renoviert; die
schwimmende Kuppel wurde auf Rollen
gesetzt.
Denkmäler für die Ewigkeit
Während die Messlatte in Europa nun auf
76,9 Zentimeter gelegt worden war, holten
die USA zum finalen Gegenschlag aus. Die
entscheidende Rolle spielten dabei wiede­
rum finanzkräftige Privatpersonen.
Es kam zunehmend in Mode, sich mit
einem großen Teleskop ein Denkmal zu
setzen. So stiftete der durch Grundbesitz
reich gewordene James Lick fast sein ge­
samtes Vermögen, um den weltgrößten
Refraktor auf einem möglichst hohen
Bernd Brinkmann
Der größte Doppelrefraktor steht in
Meudon bei Paris. Die beiden Teleskope
sind übereinander in einem kastenförmigen
Tubus untergebracht.
50
August 2011
Sterne und Weltraum
64
Berg zu errichten. Nach seinem Tod im
Jahr 1876 dauerte es aber noch zwölf Jahre,
ehe das ehrgeizige Projekt Realität wurde.
Dann stand ein 91,4-Zentimeter-Refraktor
auf dem 1283 Meter hohen Mt. Hamilton
bei San José in Kalifornien (siehe Bild S. 49
unten).
Das Lick Observatory war die erste
echte Bergsternwarte. Der 36-Zöller mit
17,4 Meter Brennweite ist in einer 18,3-Me­
ter-Kuppel untergebracht. Die zehn Meter
hohe Säule, welche die schwere deutsche
Montierung trägt, dient zugleich als Grab­
stätte. An ihrem Sockel findet sich die In­
schrift »Here lies the body of James Lick«.
Der Standort mit seiner transparenten,
ruhigen Luft und fast 300 klaren Näch­
ten im Jahr ließ spektakuläre Ergebnisse
erwarten. Und tatsächlich entdeckte im
Jahr 1892 Edward E. Barnard den fünften
Jupitermond (Amalthea). Zusammen mit
Sherbourne W. Burnham beobachtete Bar­
nard Planeten, Doppelsterne und Nebel.
Leider kam es zum erbitterten Streit
mit dem autoritären Direktor Edward
Holden. Burnham und Barnard verließen
deshalb schweren Herzens das Lick Obser­
vatory. Sie hatten bereits ein neues Ziel:
Williams Bay in Wisconsin, 140 Kilometer
nordwestlich von Chicago. Kein besonders
Rainer Sparenberg
guter Standort, aber offenbar der geeig­
nete Platz für ein neues Denkmal, dieses
Mal errichtet zu Ehren von Charles Yerkes.
Der schwerreiche Transportunternehmer
hatte sich in den Kopf gesetzt, Lick noch
zu übertreffen. Es ist das Verdienst von
George Ellery Hale, dass mit dem Geld,
Die deutsche Antwort auf Meudon: der »Große Refraktor« in Potsdam. Im
welches Yerkes der University of Chicago
Jahr 1899 errichtet, wurde das Instrument 2005 umfassend renoviert.
zur Verfügung stellte, ein monumentales
Observatorium errichtet werden konnte.
Bereits im Jahr 1893 wurde das Teleskop
auf der Chicagoer Weltausstellung präsen­
die Festbeleuchtung bei der Eröffnung der
deren Konstruktionen neue Bestmarken
Weltausstellung in Chicago ein.
zu setzen. Hier ist vor allem der Doppel­
tiert – noch ohne Objektiv. Das lieferten
Doch der monströse Yerkes-Refraktor
refraktor zu nennen, bestehend aus visuell
zwei Jahre später Alvan Clark & Sons. Es
war bereits zur Jahrhundertwende ein
und fotografisch korrigierten Objektiven
übertraf erstmals die Ein-Meter-Marke
Auslaufmodell. Sowohl seine Konstruk­
mit unterschiedlichen Öffnungen, aber
und wog 500 Kilogramm. Die Daten des
tion als auch der Standort in nur 334 Me­
ähnlichen Brennweiten. Der visuelle Teil
Instruments sind beeindruckend: 102 Zen­
ter Höhe waren nicht mehr zeitgemäß.
dient dabei als Leitrohr zum Nachführen.
timeter Öffnung, 19,8 Meter Brennweite,
Die neue Astrophysik verlangte nach
Im Jahr 1891 schufen die Brüder Henry
20 Tonnen Masse der beweglichen Teile
lichtstarken Reflektoren auf hohen Ber­
zusammen mit dem Instrumentenbauer
(siehe Bild S. 50 oben).
gen – und Hale lieferte sie. Er schuf nach­
Paul Gautier in dieser Gattung das Maß
Leider hatte der Yerkes-Refraktor kei­
einander das Mount Wilson Observatory
der Dinge: das Teleskop in Meudon bei Pa­
nen guten Start: Kurz nach der Einwei­
mit einem 2,5-Meter-Spiegel (finanziert
ris. Die Objektive haben Durchmesser von
hung im Jahr 1897 rissen die Halteseile
von John Hooker und seit 1917 aktiv) und
83 Zentimeter (visuell) und 62 Zentimeter
des Kuppelbodens, der krachend in die
das Mount Palomar Observatory mit dem
(fotografisch); die Brennweiten betragen
Tiefe stürzte. Zum Glück wurde niemand
legendären Fünf-Meter-Reflektor, der 1948
16,2 beziehungsweise 15,9 Meter. Die in
verletzt. Im Jahr 1933 erregte der 40-Zöl­
in Betrieb ging. Er trägt Hales Namen.
einem kastenförmigen Tubus zusam­
ler erneut Aufsehen: Das Licht des Sterns
Mit einem Durchmesser von etwa
mengefügten Fernrohre werden von einer
Arktur wurde auf eine Fotozelle gelenkt,
einem Meter war die Obergrenze für Re­
deutschen Montierung getragen (siehe
und der dadurch erzeugte Strom schaltete
fraktoren erreicht. Nun galt es, mit beson­
Bild S. 50 unten).
www.astronomie-heute.de
August 2011
51
65
Im Jahr 1899 ging ein vergleichbarer
Doppelrefraktor am neuen Astrophy­
sikalischen Observatorium Potsdam in
Betrieb. Kaiser Wilhelm II. kam persönlich
zur Einweihung. Die Daten sind beein­
druckend: Objektivdurchmesser 80 Zen­
timeter (fotografisch) und 50 Zentimeter
(visuell) bei jeweils 12,2 Meter Brennweite
(siehe Bild S. 51). Die Optik wurde von
Steinheil gefertigt, die deutsche Montie­
rung von Repsold. Seit 2005 ist der »Große
Refraktor« vollständig renoviert (siehe
SuW 4/2008, S. 52).
Leider erfüllte das dunkelgrün lackierte
Monstrum nicht die Erwartungen der
Astrophysiker. Mehrfach mussten beide
Objektive nachgeschliffen werden. Ein
weiteres Problem war der Standort auf
dem nur 96 Meter hohen Telegrafenberg.
Licht- und Luftverschmutzung vereitelten
regelmäßige Beobachtungen. Mit den
gleichen Problemen hatte auch das nur
zehn Kilometer südwestlich von Paris auf
165 Meter Höhe gelegene Observatorium
Meudon zu kämpfen.
Der Potsdamer Refraktor ist das größte
deutsche Linsenfernrohr. Eine in etwa
vergleichbare Größe besaß nur noch das
Treptower »Kanonenrohr« mit 21 Meter
Stefan Binnewies
Brennweite (siehe Bild links). Der kup­
pellose Refraktor mit einer Öffnung von
68 Zentimetern war die Hauptattraktion
der Berliner Gewerbeausstellung von
1897. Das von Steinheil und Hoppe ge­
Mit 21 Meter Brennweite immer noch der längste Refraktor der Welt: das
baute 160 Tonnen schwere Gerät ist heute
»Kanonenrohr« der Archenhold-Sternwarte in Berlin-Treptow.
Teil der Archenhold-Sternwarte.
Nachzügler des 20. Jahrhunderts
Die Pariser Weltausstellung im Jahr 1900
sollte zum Ruhm der Grande Nation etwas
Besonderes bieten: ein Linsenfernrohr,
das alle anderen übertreffen sollte. Schon
angesichts des schlechten Standorts war
dies ein kühner Plan, doch die Ausmaße
ließen das Projekt zu einer teuren Eintags­
fliege ohne wissenschaftlichen Nutzen
werden (siehe Bild links und SuW 12/1978,
S. 403).
Das Objektiv mit 1,25 Meter Durchmes­
ser wog 1,8 Tonnen. Schon beim YerkesArchiv Wolfgang Steinicke
Refraktor hatten sich die gewichtsbedingte
Deformation des Objektivs und eine da­
mit einhergehende Verschlechterung der
optischen Eigenschaften störend bemerk­
bar gemacht. Deshalb entschied man sich
in Paris für einen in Nord-Süd-Richtung
orientierten Horizontalrefraktor – ange­
Nur zum Anschauen, nicht zum Durchschauen geeignet: der Horizontal­
sichts der Brennweite von 57 Metern blieb
refraktor mit 1,25 Meter Öffnung während der Pariser Weltausstellung
auch keine andere Wahl!
52
August 2011
Sterne und Weltraum
66
(identisch mit Pulkowo) sowie 14,4 Meter
Brennweite und dient heute noch der As­
trometrie. Die letzten großen (klassischen)
Refraktoren gingen 1972 in Betrieb. Sie
stehen am Hida Observatory in Japan und
Wolfgang Steinicke ist
auf dem Llano del Hato in Venezuela. Es
Physiker, Autor und seit
sind Standardgeräte von Zeiss mit 65 Zen­
40 Jahren Amateurastro-
timeter Öffnung und 10,5 Meter Brenn­
nom. Seine Schwerpunkte
weite. Das Besondere am venezolanischen
sind die Geschichte der
Refraktor: Mit 3600 Meter Höhe ist er der
Astronomie, insbesondere
weltweit Höchstgelegene.
Ein trauriges Schicksal erlitt das von
die Entdeckungen der Nebel
und Sternhaufen im 19. Jahrhundert, sowie die
Grubb gebaute Yale-Columbia-Telescope
visuelle Deep-Sky-Beobachtung. Er leitet die
(66 Zentimeter Öffnung, 10,6 Meter Brenn­
VdS-Fachgruppe »Geschichte« und ist Mitglied
weite): 1925 in Johannisburg aufgestellt,
der Royal Astronomical Society.
Rainer Sparenberg
kam es 1952 zum australischen Mount
Stromlo Observatory, wo es im Januar 2003
Stefan Binnewies, Inter-
zusammen mit fünf weiteren Geräten von
nist und Pneumologe, ist in
einem Buschfeuer zerstört wurde.
freier Arztpraxis tätig. Seit
Um ein Haar wäre der Yerkes-Refraktor
30 Jahren ist er begeisterter
im Jahr 1928 übertroffen worden. Russ­
Amateur­astronom mit
land hatte bei der Firma Grubb einen
den Schwerpunkten Astro­
41-Zöller für die Pulkowo-Außenstelle in
fotografie und Finsternisex-
Das zweitgrößte Linsenfernrohr der Welt:
Simeis auf der Krim bestellt. Nachdem
kursionen. Zusätzlich arbeitete er an mehreren
das 20 Meter hohe Swedish Solar Telescope
bereits Montierung und Kuppel fertigge­
astronomischen Buchprojekten mit.
auf La Palma
stellt waren (mittlerweile vom Nachfolger
Grubb-Parsons), wiesen die Russen die
Für
Himmelsbeobachtungen
beiden Glasrohlinge mit je 105 Zentimeter
Literaturhinweise
Gussmann, E.-A., Kühn, G.: Der wieder­
erstandene Große Refraktor. Neuer
lenkte
Durchmesser als mangelhaft zurück. Das
ein ebener Spiegel, ein Coelostat, mit zwei
Projekt wurde gestoppt, und Yerkes be­
Meter Durchmesser das Sternenlicht in
hielt seinen Titel.
das waagrecht liegende Teleskop. Selbst
Im Jahr 2002 bekam der Yerkes-Refrak­
der Okularauszug war überdimensional
tor auf seine alten Tage noch einmal un­
und musste auf Schienen bewegt werden.
erwartet Konkurrenz – in Gestalt des Swe­
Beobachtungen waren schwierig und
dish Solar Telescope (SST) auf dem über
entsprechend selten. Selbst bei der Mi­
2400 Meter hohen Roque de los Mucha­
nimalvergrößerung von 500-fach betrug
chos der Kanareninsel La Palma (siehe Bild
das Gesichtsfeld nur drei Bogenminuten.
oben). Das Objektiv ist mit 107 Zentimeter
Die Projektion des Mars auf eine 400 Qua­
Durchmesser sogar größer; die genutzte
dratmeter große Leinwand erwies sich als
Öffnung beträgt aber nur 97 Zentimeter –
Fehlschlag. Nach Ende der Ausstellung
immerhin mehr als beim Lick-Refraktor.
fand das Riesenteleskop keinen Käufer
Gleichwohl kann von einer Renais­
und wurde demontiert; Objektiv und
sance des Refraktors keine Rede sein. Die
Planspiegel kamen in die Pariser Stern­
Zukunft gehört azimutalen Reflektoren,
warte. Seitdem ist der Yerkes-Refraktor
wie dem geplanten European Extremely-
wieder die Nummer eins in der Welt.
Large Telescope mit einem 39-Meter-Spie­
Obwohl weltweit Reflektoren die Ober­
gel, das Ende dieses Jahrzehnts in Betrieb
hand gewannen, wurden auch im 20. Jahr­
gehen soll. Die verbliebenen und zum Teil
hundert vereinzelt große Linsenfernrohre
noch wissenschaftlich arbeitenden groß­
gebaut. Im Jahr 1912 bekam die neue
en Refraktoren haben indes nichts von
Sternwarte
einen
ihrer Faszination verloren. Rund 40 Ge­
60-Zentimeter-Refraktor von Steinheil /
räte haben Öffnungen von 50 Zentimeter
Repsold. Nach seiner Renovierung strahlt
und mehr, sieben davon übertreffen die
das zehn Meter lange Gerät heute wieder
70-Zentimeter-Marke. Der Besucher steht
in altem Glanz.
vor eindrucksvollen Relikten einer bedeu­
Hamburg-Bergedorf
Im Jahr 1914 wurde am Allegheny
tenden Epoche der Astronomie. In Pots­
Observatory in Pittsburgh der von John
dam, Treptow, Wien, Meudon, Nizza oder
Brashear gefertigte Thaw-Refraktor aufge­
am Lick und Yerkes Observatory kann sich
stellt. Er besitzt 76,2 Zentimeter Öffnung
jeder selbst davon überzeugen.
www.astronomie-heute.de
Glanz auf dem Potsdamer Telegrafenberg. In: Sterne und Weltraum 4/2008,
S. 52 – 55
Hartl, G.: Der Refraktor der Sternwarte
Pulkowa. In: Sterne und Weltraum
7–8/1987, S. 397 – 404
King, H.: The History of the Telescope.
Dover Publications, New York 1979
Müürsepp, P.: Die alte Sternwarte Tartu.
In: Sterne und Weltraum 6/1966,
S. 129 – 131
Oberndorfer, H.: Ein Fernrohr-Unikum.
In: Sterne und Weltraum 12/1978,
S. 403 – 404
Riekher, R.: Fernrohre und ihre Meister.
VEB Verlag Technik, Leipzig 1957
Steinicke, W.: Nebel und Sternhaufen.
Geschichte ihrer Entdeckung, Beob­
achtung und Katalogisierung – von
Herschel bis zu Dreyers »New General
Catalogue«. Books on Demand, Norder­
stedt 2009
Steinicke, W., Binnewies, S.: Sternwarten. 95 astronomische Observatorien
in aller Welt. Oculum Verlag, Erlangen
2008
www.klima-luft.de/steinicke
Kataloge, Geschichte und visuelle Beob­
achtung von Deep-Sky-Objekten
August 2011
53
67
Welt der Wissenschaft: Aufbau der Galaxis
Die Sterne dieser lockeren Gruppe sind erst
kürzlich aus einer dichten Wolke aus Gas
und Staub entstanden. Die heißesten unter
ihnen haben mit ihrer Strahlung und ihrem
Wind die Reste der Wolke aufgelöst. Die
gemeinsame Bewegung der Sterne im
Raum bezeugt ihren gemeinsamen
Ursprung. Das Gebilde ist ein »offener
Sternhaufen«, seine offizielle Bezeichnung
ist NGC 4755, und sein glitzernder Anblick
hat ihm den Namen »Schatzkästlein«
eingebracht. Er ist nur zehn Millionen Jahre
alt, seine Entfernung beträgt knapp
2000 Parsec oder 6600 Lichtjahre.
In Kürze
ó Sterne entstehen in Haufen oder
Gruppen entlang der Spiralarme
unserer Galaxis. Die Haufen sind
zunächst in dichte Wolken aus
Staub und Gas eingebettet.
ó Wenn die heißesten Mitglieder
mit ihrer Strahlung und ihren
Winden die Umgebung leer gefegt
haben, werden die offenen Sternhaufen sichtbar und bieten oft ein
herrliches Schauspiel.
ó Offene Sternhaufen leben nicht
lange – im Mittel etwa 300 Millionen Jahre. Danach werden sie
schnell von den Gezeitenkräften
der Milchstraße »aufgerieben«,
und ihre Mitglieder im weiten
Umfeld zerstreut.
30
August 2011
Sterne und Weltraum
68
Offene Sternhaufen
Bausteine der Milchstraße
ESO
Eine Bestandsaufnahme der offenen Sternhaufen in der weiteren Sonnen­umbebung
hat gezeigt, dass es heute in der galaktischen Scheibe etwa 100 000 Exemplare gibt,
und dass rund 40 Prozent aller Sterne der Scheibe ihre Jugend in solchen Haufen
verbringen. Die anderen 60 Prozent bilden sich in »eingebetteten Haufen«, die sich
bereits tief im Innern der Molekülwolken auflösen, aus denen sie entstanden sind.
www.astronomie-heute.de
August 2011
31
69
Von Siegfried Röser und Elena Schilbach
mit Fug und Recht als Bausteine unserer
D
Aussage ergab sich aus der Analyse einer
ie offenen Sternhaufen gehö­
umfassenden Stichprobe naher offener
ren zu den beliebtesten Beob­
Sternhaufen, die wir im letzten Jahrzehnt
achtungsobjekten am Nacht­
durchgeführt haben und von der im Fol­
himmel. Sind sie bloß schöne
genden die Rede ist.
Episoden im weiten Feld der Galaxis, oder
Sternhaufen – wichtige
Entfernungsindikatoren
Galaxis zu bezeichnen. Diese quantitative
D
ie Bestimmung von Entfernungen
im Weltall ist eine grundlegende
Aufgabe, die sich den Astronomen immer wieder stellt. Ohne deren Kenntnis
Aufbau und Entwicklung des Milchstra­
Lockere Ansammlungen mit Gruppendynamik
ßensystems?
Das Band der Milchstraße zieht sich in
zu verstehen. Die trigonometrische
Aus zwei Gründen ist ihr Studium von
einem Großkreis über den Himmel. Es
Entfernungsbestimmung ist der erste
großer Bedeutung: Da alle ihre Mitglieder
ist die Heimat der offenen Sternhaufen,
Schritt ins Weltall, aber ihre Reichweite
praktisch gleichzeitig entstanden sind
die, im Gegensatz zu den Kugelstern­
ist durch den Durchmesser der Erdbahn
und die gleiche chemische Zusammenset­
haufen, stark zur Ebene der Galaxis hin
um die Sonne und die Genauigkeit der
zung haben, sind sie ein natürliches Labor,
konzentriert sind. Die Skalenhöhe ihrer
Messinstrumente begrenzt. Daher konn-
in dem sich Theorien zur Entstehung und
Verteilung – das ist die Höhe über der
te selbst Hipparcos, der astrometrische
Entwicklung der Sterne prüfen lassen;
galaktischen Ebene, bei der die Zahl der
Satellit der ESA, nur Entfernungen bis
und während man früher annahm, dass
Haufen im Vergleich zum galaktischen
etwa 150 Parsec mit einer Genauigkeit
offene Sternhaufen nur weniger als zehn
Äquator um den Faktor 1/e ≈ 0,37 gesun­
von besser als zehn Prozent bestimmen.
Prozent zur stellaren Population der dün­
ken ist – beträgt nur etwa 50 Parsec. Die
Mit einem anderen Verfahren, der
nen Scheibe des Milchstraßensystems bei­
Scheibe, in der sich die Population der
»Hauptreihenanpassung«, lässt sich die
tragen, wissen wir heute, dass die galak­
offenen Sternhaufen befindet, ist somit
Entfernungsbestimmung der offenen
tische Scheibe zu etwa 40 Prozent aus den
als sehr dünn zu bezeichnen, selbst wenn
Sternhaufen auf mehrere tausend Parsec
Zerfallsprodukten aller jemals gebildeten
man ihren Radius nur mit dem Abstand
ausdehnen. Die Methode beruht auf
offenen Sternhaufen besteht. Sie sind also
der Sonne vom Galaktischen Zentrum,
theoretischen Entwicklungsmodellen,
erfüllen sie eine wichtige Funktion bei
wäre zum Beispiel die Energieerzeugung der Sonne und der Sterne nicht
die für jeden Stern gegebenen Alters,
gegebener Masse und chemischer
Zusammensetzung dessen Leuchtkraft und effektive Temperatur liefern.
Daraus lassen sich über die Kenntnis
des Aufbaus der Sternatmosphären für
verschiedene Metallhäufigkeiten die
zugehörigen absoluten Helligkeiten
und Farben berechnen. Trägt man im
Farben-Helligkeits-Diagramm (FHD)
eines neugeborenen Haufens die Farben
und Helligkeiten seiner Mitglieder unter-
A Sonne
schiedlicher Masse ein, so kommen sie
alle auf der Alter-Null-Hauptreihe zu
liegen – die massereichen links oben
(hell und heiß), die massearmen rechts
unten (lichtschwach und kühl.
Später, nach Jahrmillionen der
Entwicklung, bilden die Haufenmit-
galaktisches Zentrum
1000 Parsec
S. Röser, E. Schilbach
glieder eine so genannte Isochrone
(Linie gleichen Alters, siehe Bild oben).
Solche Isochronen wurden für Sternhaufen beliebigen Alters berechnet. Die
für Sternhaufen verschiedenen Alters
berechneten Isochronen unterscheiden
sich in der absoluten Helligkeit und
So verteilen sich die 650 offenen Sternhaufen der in diesem Artikel vorgestell-
im Farbindex, bei denen sie von der
ten Untersuchung auf die galaktische Ebene. Jeder Punkt stellt einen Haufen
Alter-Null-Hauptreihe abweichen. Das
dar und hat etwa dessen gemessene Farbe. Die jüngsten Haufen, in denen
höhere Alter bewirkt ein Abknicken der
noch Sterne der Spektralklassen O und B leuchten, sind als blaue Punkte
Isochrone bei geringerer Helligkeit (oder
dar­gestellt, ihre Verteilung folgt dem Verlauf der galaktischen Spiralarme in
geringerer Masse) und größerem Farbin-
der weiteren Sonnenumgebung. Der Pfeil weist zum Galaktischen Zentrum
dex (oder geringerer Temperatur).
hin, die galaktische Rotation um das Zentrum verläuft im Uhrzeigersinn.
32
August 2011
Sterne und Weltraum
70
Alter-Null-Hauptreihe
Modelle zuverlässig sind. Die Modellparameter müssen zu Anfang
Alter:
mit Hilfe naher Sternhaufen kalibriert werden, für die möglichst
genaue trigonometrische Parallaxen vorliegen. Wie problematisch
10 Mio.
Jahre
das sein kann, zeigt der Streit um die Entfernung der Plejaden.
Der Streit brach nach den Beobachtungen des Hipparcos-Satelliten der ESA zwischen Astrometern und theoretischen Astrophy-
100 Mio.
Jahre
1000 Mio.
Jahre
0
5
10
0,0
0,5
1,0
1,5
2,0
Farbe B–V
In diesem Farben-Helligkeits-Diagramm sind die Alter-NullHauptreihe (schwarz) sowie die berechneten Isochronen (Linien
gleichen Alters) für 10, 100 und 1000 Millionen Jahre alte Sterne
dargestellt. Zum Beispiel liegen auf der blauen Kurve (Alter zehn
Millionen Jahre) Sterne mit 0,4 Sonnenmassen bei MV = 10 mag,
Sterne mit einer Sonnenmasse bei MV = 4,82 mag und Sterne mit
20 Sonnenmassen am oberen Ende der Kurve.
Aus fotometrischen Beobachtungen erhalten wir scheinbare
Helligkeiten und Farben (zum Beispiel V und B – V) für Haufenmit-
sikern aus. Hipparcos hatte die trigonometrischen Parallaxen der
Plejaden gemessen, woraus sich deren Entfernung zu 120,2 ± 1,9
Parsec ergab. Andererseits hatte die Anpassung der Hauptreihe
The Padua Group / Girardi, Marigo et al. / SuW-Grafik
absolute Helligkeit MV in mag
-5
an theoretische Isochronen im Farben-Helligkeits-Dia­gramm stets
mindestens 131,8 ± 2 Parsec ergeben. Die Differenz von mehr
als elf Parsec lässt sich durch die jeweiligen Messfehler nicht
erklären. Wir hoffen nun, dass die bevorstehende astrometrische
Gaia-Mission der ESA diese Diskrepanz auflösen wird.
A. Sandage / SuW-Grafik
-8
NGC2362
h + c Persei
-4
Plejaden (120)
M3
M 41
-2
M 41 M 11
0
M 11
Coma
Hyaden (650)
Praesepe
2
NGC752
M 67 (2500)
NGC188
H+P
752
4
glieder. Die gemessene Sequenz ist gegenüber der für absolute
Sonne
Helligkeiten berechneten, theoretischen Isochrone um einen
festen Betrag senkrecht im FHD verschoben, und zwar um den
Entfernungsmodul V – MV (die Differenz der scheinbaren und der
h + c Persei (1,2)
-6
absolute visuelle Helligkeit MV in mag
-10
6
absoluten Helligkeit in Größenklassen). Die Entfernung R ergibt
sich daraus im Prinzip einfach, und zwar nach der Beziehung
V – MV = 5 log R – 5.
8
-0,4
0
0,4
0,8
1,2
1,6
Die Wirklichkeit ist jedoch komplizierter, da gleichzeitig auch in-
Dieses Farben-Helligkeits-Diagramm zeigt die Lage der Sterne
terstellare Verfärbung und Extinktion bestimmt werden müssen.
verschiedener offener Sternhaufen sowie des Kugelhaufens M 3.
Dies verursacht eine waagerechte und zusätzlich eine senkrechte
Rechts unten liegen kühle, massearme, links oben heiße, masse-
Verschiebung der empirischen Sequenz gegenüber der theore-
reiche Sterne. Alle Sterne eines Haufens haben das gleiche Alter
tischen Isochrone im FHD.
und liegen auf der diesem Alter entsprechenden Isochronen. Aus
Es kommt hinzu, dass das Alter eines untersuchten Hau-
2,0
Farbe B–V
dem Abknickpunkt ihrer Isochronen von der Alter-Null-Hauptreihe
fens zunächst nicht bekannt ist. Deshalb vergleicht man alle
weg, besser noch aus der Lage des Knies lässt sich durch den
möglichen Isochronen mit den Beobachtungen, bis die beste
Vergleich mit theoretischen Isochronen das Alter der Haufen und
Übereinstimmung gefunden ist. Die Methode liefert recht gute
ihre Entfernung ermitteln. Für einige Haufen ist in Klammern das
Abschätzungen für Entfernung, Alter und interstellare Verfärbung
so ermittelte Alter (in Millionen Jahren) angegeben: Es variiert
der Sternhaufen. Voraussetzung ist jedoch, dass die theoretischen
zwischen 1,2 und 2500 Millionen Jahren.
www.astronomie-heute.de
August 2011
33
71
etwa 8500 Parsec, gleichsetzt. (Ein Parsec
ist die Entfernung, aus welcher der mittle­
re Radius der Erdbahn um die Sonne – die
Astronomische Einheit – unter dem Win­
kel von einer Bogensekunde erscheint; sie
entspricht etwa 3,26 Lichtjahren.)
Anders als Kugelsternhaufen erschei­
nen offene Haufen als lockere, unregelmä­
ßige Ansammlungen von Sternen und mit
weniger Mitgliedern, so dass es manch­
mal schwierig ist, sie vom allgemeinen
Sternfeld zu trennen. Aber alle Mitglieder
eines offenen Haufens sind am gleichen
Ort und zur gleichen Zeit entstanden und
erinnern sich während ihres gesamten
Sternenlebens an ihre Geburt: Sie alle ...
ó sind gleich weit von der Erde entfernt,
ó haben die gleiche chemische Zusam­
mensetzung,
ó sind gleich alt und
ó bewegen sich mit annähernd gleicher
ESO
Geschwindigkeit durch den Raum.
Das dynamische Verhalten der Haufen­
mitglieder bewirkt, dass sie für einige Zeit
zusammenbleiben.
Schließlich
Der junge offene Sternhaufen NGC 3603 enthält neben mehr als 50 hellen
jedoch
und massereichen O-Sternen mit insgesamt mindestens 1000 Sonnenmas-
wer­den sie von den Gezeitenkräften der
Milchstraße auseinandergetrieben. Wir
sen auch zahlreiche Sterne, deren Masse geringer ist als diejenige der Sonne.
kennen deshalb keine offenen Sternhau­
Alle Mitglieder sind innerhalb der letzten Million Jahre aus einer riesigen
fen, die so alt wären wie die galaktische
Gas- und Staubwolke entstanden. Das Bild ist ein Komposit aus Aufnahmen
in den Wellenlängenbereichen J, H und Ks im nahen Infrarot, das den Staub
Scheibe selbst.
durchdringt und auch Sterne im Inneren der Wolke sichtbar macht.
Betrachten wir die Verteilung der 650
von uns untersuchten offenen Stern­
haufen in der Sonnenumgebung, pro­
jiziert auf die galaktische Ebene (siehe
Bild auf S. 32). Ein solches Bild würden
Astronomen in der »Black-Eye-Galaxie«
M 64 erhalten, sollten sie mit ihrem
Weltraumteleskop unser Milchstraßen­
system beobachten. Diese Galaxie steht
senkrecht über der Ebene unserer Gala­
xis, und sie ist so weit von uns entfernt,
dass das Bild gerade einer Aufnahme des
Weltraumteleskops Hubble mit der ACSKamera entsprechen würde. Die Darstel­
lung zeigt, dass die jüngsten und hellsten
offenen Sternhaufen die Spiralstruktur
des Milchstraßensystems nachzeichnen.
Dies hängt damit zusammen, dass Sterne
bevorzugt in Spiralarmen entstehen.
Auch
die
jüngsten,
massereichen
Sterne der Spektralklassen O und B zeich­
nen die Spiralstruktur nach, allerdings
nicht in der gleichen Klarheit. Denn ihre
Entfernung lässt sich weniger genau be­
haufen. Deshalb haben die offenen Hau­
fen große Bedeutung für die Bestimmung
astronomischer
Entfernungen
Kasten auf S. 32/33).
34
August 2011
(siehe
NASA / ESA / HST
stimmen als diejenige der offenen Stern­
Sterne und Weltraum
72
Viele eingebettete Sternhaufen
lösen sich schon sehr früh auf
Charles und Elizabeth Lada haben sich
gung steckende Energie der Sterne halb
besonders für die Gesamtmassen der
so groß ist wie ihre potenzielle, durch die
Sterne entstehen in Gruppen oder Hau­
eingebetteten Haufen interessiert. Die Be­
vorhandene Masse und deren Verteilung
fen im Innern von dichten, mit Staub
stimmung der Massen ganzer Sternhau­
bestimmte Energie. Die erforderlichen
angereicherten Molekülwolken. Folglich
fen ist kompliziert, und unterschiedliche
Beobachtungen sind kompliziert und feh­
sind solche Sternentstehungsgebiete im
Methoden führen oft zu widersprüch­
leranfällig. Bei eingebetteten Haufen wird
sichtbaren Licht durch die diffuse Materie
lichen Ergebnissen. Am einfachsten wäre
die Massenbestimmung zusätzlich durch
in ihrer Umgebung weit gehend verhüllt.
es, alle Mitglieder eines Sternhaufens
die Extinktion erschwert. Charles und Eli­
Infrarotes Licht hingegen wird durch
zu zählen,und jedem einzelnen entspre­
zabeth Lada haben die vorhandenen Daten
das Gas und den Staub weit weniger ge­
chend seiner Helligkeit eine Masse zuzu­
aus der Literatur zusammengestellt, die
schwächt, so dass Aufnahmen in diesem
ordnen. Die Addition der Einzelmassen
Haufenmitglieder gezählt, ihre Massen
Wellenlängenbereich den Blick auf gerade
ergäbe dann die Gesamtmasse. Allerdings
bestimmt, zu kleineren Sternmassen ex­
entstehende Sternhaufen gestatten (siehe
lassen sich die Sterne nur bis zu einer be­
trapoliert und damit die in der Grafik auf
die Bilder links und unten).
stimmten Grenzhelligkeit erkennen, und
S. 36 oben dargestellte Massenfunktion
Junge Sterne sind zunächst noch in die
man muss extrapolieren, wie viele schwä­
der ein­gebetteten Sternhaufen abgeleitet.
Gas- und Staubwolken eingebettet, aus de­
chere Sterne es zusätzlich gibt. Die­se Ex­
Sie gibt an, wie viele Haufen der Masse M
nen sie kürzlich entstanden sind. Vor eini­
trapolation ist unsicher. Alternativ nutzt
in den einzelnen Massenintervallen dM
gen Jahren haben die US-amerikanischen
man die Tatsache, dass die Sternhaufen
vorhanden sind.
Astronomen
den
Charles
und
Elizabeth
Gezeitenkräften
der
Milchstraße
Wie aus dieser Grafik ersichtlich, liegen
Lada eine umfassende Sammlung von
ausgesetzt sind. Die am Rand eines Hau­
die Massen eingebetteter Sternhaufen im
Messungen an solchen »eingebetteten
fens liegenden Sterne sind gerade noch
Bereich zwischen 10 und 3000 Sonnen­
Sternhaufen« zusammengestellt, als de­
durch Gravitation an ihn gebunden und
massen, und die Verteilung folgt in die­
ren Prototyp der unten zweimal gezeigte
können nicht entweichen. Deshalb lässt
innere Teil des Orionnebels gilt: Während
sich aus der Größe des Haufens auf seine
sem Bereich einem Potenzgesetz der Form
n(M) = Ma dM mit dem Exponenten
im Optischen wenig mehr als die vier
Masse schließen; die so bestimmten Mas­
a = –1,7. Ein Exponent mit dem Wert a = –2
Trapezsterne sichtbar sind, erscheint im
senwerte heißen »Gezeitenmassen«, von
würde bedeuten, dass jedes Massenin­
Infraroten ein Sternhaufen mit tausenden
ihnen wird noch die Rede sein.
tervall gleich viel zur Gesamtmasse aller
Mitgliedern, von denen die ältesten we­
Auch aus der gemessenen Geschwin­
eingebetteten Sternhaufen beiträgt. Wäre
nige Millionen, die jüngsten nur 500 000
digkeitsverteilung der Mitglieder lässt sich
der Exponent kleiner als –2, so trügen die
Jahre alt sind. Und sehr wahrscheinlich
auf die Masse der Haufen schließen, da im
vielen massearmen Haufen den Löwen­
entstehen dort auch heute noch Sterne.
Gleichgewicht die kinetische, in der Bewe­
anteil. Der Exponent –1,7 besagt, dass die
Der Orionnebel ist uns als farbenprächtiges
Gebilde aus leuchtendem Gas und dunklen
Staubstrukturen vertraut, denn so erscheint
er im sichtbaren Licht. Nur die Trapezsterne
in seiner Mitte und wenige andere sind zu
erkennen, und früher kam niemand auf die
Idee, dass sich in der dichten Wolke noch
weitere Sterne verbergen (linkes Bild). Ganz
anders als im Sichtbaren sieht die Umgebung der Trapezsterne im nahen Infrarot
M. McCaughrean / ESO
aus. Das infrarote Licht durchdringt die
www.astronomie-heute.de
vorgelagerten Staubmassen, und nun zeigt
sich, dass das Trapez in Wahrheit aus den
fünf hellsten Sternen eines großen
Sternhaufens mit mehreren tausend
Mitgliedern besteht (rechtes Bild).
August 2011
35
73
wenigen
massereichen
10 000
eingebetteten
massen gefunden. Erst in den letzten Jah­
ren hat man einige wenige entdeckt. Alle
eingebetteten Sternhaufen sind ähnlich
jung wie NGC 3603 oder der Sternhaufen
um das Trapez im Orionnebel, die ältesten
sind nur etwa fünf Millionen Jahre alt.
Die Auswertung der Sammlung von
Charles und Elizabeth Lada hat gezeigt,
dass in der galaktischen Scheibe die Ent­
stehungsrate der eingebetteten Sternhau­
fen pro Flächeneinheit und pro Million
fen« nach Lada und
Lada lässt sich durch
ein Potenzgesetz
mit dem Exponenten a = -1,7
darstellen. Die
100
dunkle Fläche zeigt
die wenigen in den
letzten Jahren
gefundenen
10
massereichen
1
Sternhaufen, von denen hier die Rede sein
10
wird. Dies führte zu dem Schluss, dass
betteten Sternhau-
später gefundene
massereiche Haufen
1000
Jahre etwa zehnmal so hoch ist wie die
Entstehungsrate der klassischen offenen
lung der »einge-
Lada 2010 / SuW-Grafik
mit Massen größer als etwa 3000 Sonnen­
Anzahl der Sternhaufen pro Massenintervall
samtmasse beitragen. Interessanterweise
werden kaum eingebettete Sternhaufen
Die Massenvertei-
Massenverteilung der
»eingebetteten Sternhaufen«
zu kleineren und größeren Massen extrapoliertes Potenzgesetz
Sternhaufen den Hauptanteil zur Ge­
100
1000
10 000
105
eingebetteten
Sternhaufen.
106
Masse der Sternhaufen in Sonnenmassen
sich etwa 90 Prozent der eingebetteten
Sternhaufen schon nach wenigen Milli­
onen Jahren auflösen und somit nicht zu
offenen Sternhaufen werden. Dieses Phä­
nomen wird als »Kindersterblichkeit« der
eingebetteten Haufen bezeichnet.
Mit den überlebenden zehn Prozent
wollen wir uns in der Folge beschäftigen.
Die­se Haufen haben die sie umgebende
Gas- und Staubwolke im Wesentlichen ver­
loren und sind nun im sichtbaren Licht zu
beobachten. Unsere Untersuchungen aus
den letzten Jahren sprechen dafür, dass
aus diesen zehn Prozent der eingebetteten
Haufen letztlich die klassischen offenen
Sternhaufen hervorgegangen sind.
Klassische offene Sternhaufen
Statistisch aussagefähige Ergebnisse zur
gesamten Population der offenen Stern­
haufen erhält man nur, wenn man eine
große Stichprobe gleicher Qualität mit
wissenschaftlich überprüfbaren Metho­
den untersucht. Eingehende Untersu­
chungen einzelner Objekte wie der Pleja­
den, der Hyaden, von Praesepe oder M 67
haben ihre Bedeutung, aber das Stu­dium
der Gesamtheit der offenen Sternhaufen
in der galaktischen Scheibe erfordert eine
größere Stichprobe.
Vor einigen Jahren haben wir zu­
Die meisten hellen Sterne im Zentralteil
und Potsdam mit einer systematischen
der Plejaden sind Mitglieder des
Untersuchung der offenen Sternhaufen
Haufens, aber die beiden durch Pfeile
in Sonnenumgebung begonnen. Unsere
markierten Sterne stehen im Vorder-
Arbeitsgrundlage war eine vollständige
grund, denn ihre allzu großen Eigenbe-
Himmelsdurchmusterung, bestehend aus
dem Tycho-2-Katalog, der die astrome­
trischen und fotometrischen Messungen
36
August 2011
Reinhold Wittich
sammen mit Kollegen in Kiew, Moskau
wegungen passen nicht zu denen der
Plejaden (siehe das Bild auf S. 38).).
Sterne und Weltraum
74
ED-Apochromaten:
NEU! 1.849,-€*
8x50 Sucher ohne Aufpreis!
(nur ED 127)
des Hipparcos-Satelliten sowie die Daten
der Test in den allermeisten Fällen negativ
des Astrographischen Katalogs aus dem
aus. Jedoch fanden wir 520 Sternhau­
frühen 20. Jahrhundert enthält. Somit
fen, die bereits in einer 1700 Mitglieder
standen uns für 2,5 Millionen Sterne Ei­
zählenden Liste möglicher Sternhaufen
genbewegungen und Fotometrie im Blau­
aufgeführt waren. Zusätzlich entdeckten
en und im Visuellen zur Verfügung.
wir im Tycho-2-Katalog 130 neue Stern­
Tycho-2 ist vollständig bis zur schein­
haufen, die zuvor noch nirgends ver­
baren visuellen Helligkeit V = 11,5 mag.
zeichnet waren, so dass die Gesamtzahl
In diesen Daten haben wir nach der
der bestätigten Haufen 650 beträgt. Ihre
folgenden objektiven Methode offene
Verteilung in der galaktischen Ebene zeigt
Sternhaufen gesucht: Am ganzen Him­
das Bild auf S. 32. Die Untersuchung der
mel haben wir unseren Rechner für jeden
räumlichen Verteilung unserer Stichprobe
Stern heller als V = 9,5 mag prüfen lassen,
ergab, dass sie bis zu einem Abstand von
ob die Sterndichte in seiner Umgebung
850 Parsec von der Sonne vollständig ist.
erhöht war, ob es in einer eventuellen
In diesem Bereich liegen 250 offene Hau­
Dichteerhöhung weitere Sterne gleicher
fen. Daraus können wir auf deren Gesamt­
Eigenbewegung gab und ob diese Sterne
zahl schließen, die sich gegenwärtig in der
im
auf
galaktischen Scheibe befinden. Es sind
einer einheitlichen Isochronen lagen. Es
etwa 100 000 – weitaus mehr als die Zahl
gibt insgesamt etwa 250 000 Sterne heller
der Kugelsternhaufen, die wohl nur einige
als V = 9,5 mag, und erwartungsgemäß fiel
hundert Mitglieder beträgt.
Farben-Helligkeits-Diagramm
Woran erkennt man die echten Haufenmitglieder?
Sternhaufen fallen dadurch auf, dass
an der betreffenden Stelle des Himmels
die Konzentration absolut heller Sterne
frühen Spektraltyps höher ist als in der
ED 127 Carbon
Die Carbonausführung wiegt nur 6,2kg mit Tauschutzkappe
und Rohrschellen, gegenüber 9,9kg im Alutubus! Und das ohne Aufpreis!
Jetzt nur:
898,-€*
979,-€*
ED 80
Art.Nr.:
Öffnung:
Brennweite:
Fotografische Blende:
Auflösungsvermögen:
Max. Grenzgröße:
Max. sinnvolle Vergrößerung:
Bildfeld im APS-C Format**:
Tubuslänge (inkl. Taukappe):
Gewicht:
Optisches Design:
Vergütung der Linsen:
Glasmaterial Objektivlinse:
Auch erhältlich als:
Lieferumfang:
ED 80
ED 127 Carbon
0112104
0112130
80 mm (3,1") 127 mm (5")
480 mm
952,5 mm
f/6
f/7,5
1,45"
0,9"
12,0 MAG
13,0 MAG
160-fach
255-fach
2,86° x 1,9°
1,44° x 0,96°
48 cm
99 cm
3,4 kg
6,2 kg
3 Linsen mit Luftspalt und ED-Element
EMD™ (Enhanced Multilayer Deposition)
HOYA® ED Glas - FCD1
ED 102 (Art.Nr. 0112104) 1.499€*
Optischer Tubus; Prismenschiene 360° rotierbar mit Fotoanschlussgewinde ¼“
und 3/8“ (nur ED 80); Rohrschellen mit Handgriff und Prismenschiene (ED 102/127);
1:10 Crayford-OAZ; 2“ Zenitspiegel; 25mm Okular mit 70° GF; Tauschutzkappe
(ED 127 in Carbon); Staubschutzdeckel; passender Bildfeldebner mit Kamerabajonett für Canon EOS oder Nikon; 8x50 Sucher beleuchtet mit aufrechtem Bild
(nur ED127 Carbon); stabiler Transportkoffer
Optional für ED 80/102:
8x50 Sucher beleuchtet mit aufrechtem Bild. Preis 129,- €
Star Power!
Umgebung; dies allein will aber noch
nicht viel heißen, denn zunächst sind die
Entfernungen der einzelnen Sterne ja un­
bekannt. Ein schönes Beispiel hierfür sind
die Plejaden, deren Zentralteil im neben­
stehenden Bild gezeigt wird. Die beiden
mit Pfeilen markierten Sterne sechster
Größe sind Vordergrundsterne und ge­
stark variable Extinktion kann an einer
Stelle eine höhere Sternkonzentration als
in der Umgebung vortäuschen.
Das erste starke Kriterium dafür, dass
ein offener Sternhaufen ein einheitliches
Gebilde ist, ist das kinematische – die
gemeinsame Bewegung aller seiner Mit­
glieder im Raum. Dies bedeutet, dass die
Radialgeschwindigkeiten und Eigenbewe­
gungen aller echten Mitglieder nur we­
nig um ihren gemeinsamen Mittelwert
streuen. Über die Eigenbewegungen von
Sternen gab es schon immer mehr Infor­
mation, als über deren Radialgeschwin­
digkeiten, deshalb hat man zunächst Ei­
genbewegungen von Sternen verwendet,
um damit Mitglieder offener Haufen zu
finden.
Eigenbewegungen bestimmt man aus
100° Okulare:
Brennweite:
Art.Nr.:
Augenabstand:
Scheinb. Gesichtsfeld:
Feldblende (virtuell):
Optische Elemente:
Gewicht:
Höhe:
Durchmesser:
Preis:
82° Okulare:
9mm
0218409
12,5mm
100°
15,7mm
9
680g
120,0mm
59,0mm
399,- €*
14mm
0218414
14.5mm
100°
24.4mm
9
890g
123,5mm
69,0mm
439,- €*
20mm
0218420
14,4mm
100°
34,8mm
9
990g
122,5mm
69,0mm
519,- €*
Brennw.:
Art.Nr.:
Steck Ø:
Preis:
4,7mm
0218804
1¼"
159,- €*
6,7mm
0218806
1¼"
159,- €*
8,8mm
0218808
1¼"
179,- €*
11mm
0218811
1¼"
179,- €*
Brennw.:
Art.Nr.:
Steck Ø:
Preis:
14mm
0218814
1¼"
179,- €*
18mm
0218818
2"
199,- €*
24mm
0218824
2"
298,- €*
30mm
0218830
2"
329,- €*
Features der 100° und 82° Okulare:
Wasserdicht und stickstoffgefüllt!
Vergütung: EMD™ (Enhanced Multilayer Deposition)
Gehäuse: schwarz eloxiertes Aluminium; Abgedichtet; Stickstoffgefüllt;
Edelstahl, konische Sicherungsnut
Sonstiges: Laserbeschriftung mit Seriennummer; Gummiarmierte Grifffläche; Gummiaugenmuschel umklappbar; Gewinde für Standard 2"
Filter
den Differenzen der Sternpositionen über
mehrere Beob­achtungsepochen hinweg.
Nehmen wir als Beispiel die Plejaden: Wie
www.astronomie-heute.de
© 2011 Meade Instruments Europe GmbH &Co. KG. Alle Rechte vorbehalten. Änderungen und Irrtümer vorbehalten.
*Unverbindliche Preisempfehlung in Euro (D). ** 24 x 16 mm, verwendet bei den meisten Digital-Spiegelreflexkameras
hören nicht zum Sternhaufen. Auch eine
MEADE Instruments Europe GmbH & Co. KG
Gutenbergstraße 2 • 46414 Rhede/Westf.
2011
Tel.: (0 28 72) 80 74 - August
300 • FAX:
(0 28 72)37
80 74 - 333
Internet: www.meade.de • E-Mail: [email protected]
75
100
Mitglieder der Plejaden
die Plejaden in Rektaszension und Deklination untersucht. Dazu
haben wir 20 Schmidt-Platten der Thüringer Landessternwarte
in Tautenburg vermessen, die über einen Zeitraum von 25 Jahren aufgenommen worden waren. Das Ergebnis ist im nebenstehenden Diagramm dargestellt.
Die gemessenen Eigenbewegungen zeigen zwei Konzentra­
tionen. Die allermeisten untersuchten Sterne konzentrieren sich
in der Nähe des Nullpunkts – sie befinden sich in großer Entfernung im Hintergrund. Dagegen gibt die kleine Konzentration
von nur etwa 750 Sternen bei (+20, -40) Millibogensekunden
pro Jahr die gemeinsame Eigenbewegung der echten Plejadenmitglieder wieder. Sterne mit (den Beträgen nach) noch höheren
Eigenbewegungen befinden sich im Vordergrund.
60
40
20
0
-20
-40
Schilbach et al. 1995
zur 17. Größe in einem 16 Quadratgrad großen Feld um
80
Eigenbewegung in Deklination
in Millibogensekunden pro Jahr
W
ir haben die Eigenbewegungen von 40 000 Sternen bis
-60
-80
-100
-100
-50
0
50
100
Eigenbewegung in Rektaszension in Millibogensekunden pro Jahr
der Kasten oben zeigt, haben die allermei­
nen (siehe die Bilder unten rechts und den
Stern. Er ist später entstanden und mas­
sten Sterne in der Umgebung der Plejaden
Kasten auf Seite 32/33).
sereicher, entwickelt sich schneller und
nahezu
verschwindende
Eigenbewe­
Aufgrund der Lage der Isochrone eines
erscheint uns dennoch jünger und blauer
gungen – sie gehören zum Hintergrund.
Haufens im Farben-Helligkeits-Diagramm
als die übrigen Haufenmitglieder auf der
Nur etwa 2,5 Prozent haben stark abwei­
lässt sich sowohl seine Entfernung als auch
Hauptreihe. Solche Sterne werden »Blaue
chende, aber einheitliche Eigenbewe­
die Größe der interstellaren Staubextink­
Nachzügler« genannt, sie liegen oberhalb
gungen und sind echte Mitglieder der Ple­
tion im Vordergrund bestimmen. Dieje­
des Abknickpunkts auf der Hauptreihe,
jaden. Die beiden im Bild auf S. 36/37 mit
nige Isochrone, die zur beobachteten Ver­
und ihre Zahl ist im Vergleich zur Gesamt­
Pfeilen markierten Sterne liegen im Bild
teilung im Farben-Helligkeits-Diagramm
zahl der Haufenmitglieder sehr gering.
oben weder in der Konzentration um den
am besten passt, liefert das Alter des
Alternativ zu dieser Erklärung könnte
Nullpunkt noch bei den Plejaden, sondern
Sternhaufens. Grob gesagt, ist dieses Al­
in einem engen Doppelstern von der mas­
Weil alle Mitglieder eines Haufens gemeinsam entstanden
sind, dienen sie zum Test für unser Verständnis der Sterne.
sereicheren, bereits zu einem Riesen ent­
wickelten Komponente Massenübertra­
gung auf die masseärmere stattgefunden
haben. Letztere entwickelt sich dann als
besitzen große Eigenbewegungen. Also
ter durch den Punkt gegeben, an dem die
müssen sie weit im Vordergrund stehen.
Isochrone von der Alter-Null-Hauptreihe
scheinbar jüngerer, massereicherer Stern.
Weniger eindeutig als dieses dyna­
abzweigt. Auf der Alter-Null-Hauptreihe
mische Kriterium für die Mitgliedschaft
gehört zu diesem Punkt eine ganz be­
Die Population der Sternhaufen
in unserer Umgebung
ist die Forderung, dass die Mitglieder
stimmte Sternmasse. Alle Sterne größerer
Nachdem wir die Mitglieder der 650 Hau­
eines offenen Sternhaufens alle gleich alt
Masse haben die Alter-Null-Hauptreihe
fen unserer Stichprobe mit den verfüg­
sein müssen. Es könnten ja im Haufen im­
bereits verlassen, diejenigen geringerer
baren Daten so gut wie möglich bestimmt
mer wieder neue Sterne entstanden sein,
Masse liegen noch auf ihr. Wenn, wie oben
haben, wenden wir uns den integralen
bis der Vorrat an Gas und Staub durch
angenommen, alle Sterne eines Haufens
Eigenschaften der offenen Sternhaufen in
Sternbildung aufgebraucht ist. Dennoch
gleichzeitig entstanden sind, dürfte es
der Sonnenumgebung zu. Es geht um die
können wir davon ausgehen, dass Sterne
keine Mitglieder geben, die oberhalb des
Fragen: Wie groß, wie massereich, wie alt
in einem Haufen gleichzeitig gebildet
Abknickpunkts auf der Alter-Null-Haupt­
und wie hell sind die offenen Sternhaufen
werden oder zumindest innerhalb eines
reihe liegen. Auf die große Mehrzahl der
in der Milchstraße? Wir wollen die »ein­
Zeitraums entstehen, der kurz ist im Ver­
Fälle trifft dies auch zu.
gleich zu seiner Lebensdauer. Trägt man
Dennoch gibt es in einzelnen Haufen
facheren« Fragen zuerst behandeln.
Die Bestimmung des Alters wurde be­
nämlich die gemessenen scheinbaren
(alle älter als eine Milliarde Jahre) solche
reits besprochen, ähnlich unkompliziert
Helligkeiten und Farben eines Sternfelds
eigentlich verbotenen Mitglieder. Ihre
ergibt sich auch die Gesamtleuchtkraft
um einen offenen Haufen herum in ein
Mitgliedschaft wird durch die Messung ih­
der Sternhaufen. Man beginnt in jedem
Farben-Helligkeits-Diagramm ein, so stellt
rer Eigenbewegung bestätigt. Wie lässt sich
Wellenlängenbereich mit dem jeweils
man fest, dass sich die – zum Beispiel aus
dies erklären? Im zentralen Bereich eines
hellsten Mitglied und schreitet dann
Eigenbewegungen bestimmten – echten
Sternhaufens kommt es immer wieder zu
zu den schwächeren Mitgliedern fort,
Mitglieder des Haufens auf einer gemein­
Kollisionen zwischen Sternen. Wenn zwei
indem man jeweils die Leuchtkraft, das
samen Sequenz anordnen, die seinem Al­
Sterne dabei verschmelzen, bildet sich
heißt die pro Zeiteinheit abgestrahlte
ter entspricht – der so genannten Isochro­
aus der Summe ihrer Massen ein neuer
Energie, aufsummiert. Dabei zeigt sich,
38
August 2011
Sterne und Weltraum
76
dass die Leuchtkraft aller Sternhaufen
Anders als beim Palomar Sky Survey
Molekülwolke Sterne entstehen, geschieht
meist von dem halben Dutzend ihrer
ist die Fotometrie des Two-Micron-All-
dies zuerst im dichtesten Teil. Hier ist
hellsten Sterne bestimmt wird. Wie viele
Sky-Survey (2MASS) im nahen Infrarot
auch die Wahrscheinlichkeit für enge Be­
weitere Mitglieder ein Haufen auch hat,
zwar ausgezeichnet, aber er verzeichnet
gegnungen am größten. Dadurch erhalten
sie tragen zur Gesamtleuchtkraft kaum
keine Eigenbewegungen, ist also auch nur
massearme Sterne sehr bald höhere Ge­
noch bei. Der Grund hierfür ist, dass die
bedingt hilfreich. Die Grenzgröße der von
schwindigkeiten und können sich weiter
massereichen Sterne wesentlich mehr En­
uns benutzten Durchmusterung auf der
vom Zentrum entfernen, während die
ergie pro Masseneinheit erzeugen als die
Basis von Tycho-2 beträgt V = 11,5 mag,
massereichen langsamer bleiben und sich
massearmen.
Die Frage nach der Größe der Stern­
wir können also in den Haufen nur die
stärker zum Zentrum hin konzentrieren.
Verteilung der helleren Sterne bestimmen
Hier entwickeln sie auch bald stellare Win­
haufen scheint einfach zu sein: Man muss
und den Winkeldurchmesser über die Be­
de, die ihre Umgebung so weit leer fegen,
doch nur an den Himmel schauen! Jedoch
stimmung der Mitgliedschaft, sowie den
dass sich dort keine weiteren Sterne mehr
erweist sie sich aus mehreren Gründen
linearen Durchmesser über die Bestim­
bilden.
als ähnlich schwierig wie diejenigen
mung der Entfernung ableiten.
Wenn also Massensegregation vorliegt,
nach der Leuchtkaft oder dem Alter. Ba­
Es ergab sich dabei auch, dass sich in
muss die Durchmusterung so empfindlich
nal ist die Tatsache, dass früher das Ge­
den Sternhaufen die massereichsten und
sein, dass der wesentliche Teil des Massen­
sichtsfeld eines Teleskops die scheinbare
somit hellsten Sterne verstärkt im Zen­
spektrums, bis zu hinreichend massear­
Größe eines Haufens begrenzte. Hatte
trum konzentrieren – dies wird als »Mas­
men Sternen, erfasst wird.
man seinen dichten Zentralteil erfasst,
sensegregation» bezeichnet. Auch Simula­
Wie lässt sich der »Rand« oder der Ra­
so gab man sich zufrieden, und leitete so
tionen der Entwicklung von Sternhaufen
dius eines Haufens physikalisch sinnvoll
einen zu kleinen Haufendurchmesser ab.
zeigen, dass massereiche Sterne sich mit
bestimmen? Eine Definition lautet: Der
Jedoch hat auch eine flächendeckende
der Zeit verstärkt im Zentrum der Haufen
Rand ist dadurch gegeben, dass sich hier
Himmelsdurchmusterung ihre Probleme.
ansammeln. Verständlich ist dies, wenn
die Gravitationswirkung des Haufens
Bei tiefen Durchmusterungen, etwa beim
man annimmt, dass sich eine Gleichver­
und diejenige der Milchstraße gerade die
Palomar Sky Survey, reicht die fotome­
teilung der kinetischen Energie einstellt.
trische Genauigkeit bei weitem nicht
Dann besitzen die massereichen Sterne
aus, um Mitglieder von Nichtmitgliedern
im Mittel geringere Geschwindigkeiten
Diese Farben-Helligkeits-Diagramme
zu unterscheiden, und auch die Quali­
als die massearmen. Letztere bewegen
einiger naher offener Sternhaufen basieren
tät der Eigenbewegungen ist zu gering.
sich also weiter vom Gravitationszentrum
auf den Messungen des Hipparcos-Satel-
Denn geht man in einem Sternhaufen
des Haufens weg, unterliegen dadurch
liten. Aufgetragen ist die absolute Hellig-
von den helleren zu den schwächeren
verstärkt den Gezeitenkräften der Milch­
keit gegen die Farbe. Die durch Einzelsterne
Sternen, so nimmt die Genauigkeit der
straße und gehen dem Haufen leichter
definierte Hauptreihe ist sehr gut erkenn-
Positionsmessungen, und folglich auch
verloren.
bar. Die darüberliegenden Haufenmitglieder sind Doppelsterne, die nicht in
der Eigenbewegungen ab. Das bedeutet: Je
Aber auch im Sternhaufen um das
lichtschwächer und weiter entfernt die zu
Trapez im Orionnebel sind die masse­
vermessenden Sterne sind, desto genauer
reichsten Sterne – trotz seiner Jugend –
Einzelsterne aufgelöst werden konnten. Die
Farbe B2–V1 bezieht sich auf das Genfer
muss die Messung sein. Dieses Problem
bereits im Zentrum konzentriert. Man
fotometrische System, das sich leicht vom
lässt sich nicht umgehen.
kann dies so verstehen: Wenn in einer
Standardsystem unterscheidet.
0
5
Hyaden
Praesepe
Großer Bär
Haar der Berenike
NGC7092
0
Nach van Leeuwen 2009 / SuW-Grafik
absolute Helligkeit MV in mag
absolute Helligkeit MV in mag
Plejaden
Blanco 1
NGC 2516
5
0
0,5
Farbe B2– V1
www.astronomie-heute.de
0
0,5
Farbe B2– V1
August 2011
39
1,0
Allerdings
zeigen
Computersimula­
tionen, dass die Lebenserwartung der
Siegfried Röser, Elena Schilbach/ SuW-Grafik
Anzahl der Sternhaufen pro Million Jahre
77
0,1
0,01
0,001
10
100
1000
Alter der Sternhaufen in Millionen Jahre
Haufen stark von ihrer Masse abhängt: Je
massereicher ein Haufen ist, umso länger
dauert es, bis ihn die Gezeitenkräfte der
Milchstraße »zerrieben« haben. Weiter
finden wir, dass die Massenverteilung aller
Sternhaufen in der Sonnenumgebung von
den massearmen Haufen dominiert wird.
Die Massenfunktion der jüngsten offenen
Sternhaufen ist jener der eingebetteten
Haufen ähnlich (siehe Grafik auf S. 36).
Ein weiterer Befund: Unter den jüngsten
offenen Sternhaufen ist der Anteil derer
mit Massen unter 1000 Sonnenmassen
Die Altersverteilung der offenen Sternhaufen in Sonnenumgebung zeigt,
wesentlich geringer als bei den älteren
dass die Zahl der Haufen ab einem Alter von einigen hundert Millionen
Haufen. Der flache Verlauf der Massenver­
Jahren dramatisch abnimmt. Die rote Kurve stellt einen exponentiellen
teilung bei den jüngsten Haufen bedeutet,
Abfall mit einer Zerfallszeit von 330 Millionen Jahren dar.
dass hier die massereicheren Haufen am
meisten zur Gesamtmasse beitragen.
In der Tat zeigt sich, dass die jüngsten
Waage halten. Innerhalb dieses »Gezeiten­
Ort des Haufens, so ist auch die Haufen­
Haufen im Mittel 4500 Sonnenmassen
radius« gehören die Sterne zum Haufen,
masse gegeben. Damit waren die Massen
besitzen, die durchschnittliche Masse der
außerhalb haben sie ihn verlassen. Wir
aller Haufen unserer Liste bestimmt.
Haufen in Sonnenumgebung beträgt dage­
finden eine Analogie im Sonne-Erde-
gen nur 700 Sonnenmassen. Offenbar ver­
innerhalb des Gezeitenradius des Erde-
Die zeitliche Entwicklung offener Sternhaufen
Mond-Systems, er ist somit ein Trabant
Damit liegen die wichtigsten Informati­
Sternhaufen verlieren ihre Masse zum
der Erde und kein Planet.
onen vor, um die Entwicklung der offenen
Teil durch Entwicklung und Sterben ihrer
Vor fast 50 Jahren hat der amerika­
Sternhaufen in der Sonnenumgebung zu
massereichsten Mitglieder in den ersten
nische Astronom Ivan King eine Theorie
beschreiben. Wir kennen die Häufigkeits­
Millionen Jahren. Allerdings kommt der
entwickelt, wie man aus der Verteilung
verteilung Ihres Alters, ihrer Leuchtkraft
hauptsächliche Massenverlust dadurch zu
der Sterne eines Haufens am Himmel auf
und Masse. Betrachten wir zunächst die
Stande, weil den Haufen vor allem mas­
dessen Gezeitenradius schließen kann.
Altersverteilung der Haufen in der Grafik
searme Sterne durch die Gezeitenwirkung
Die Anwendung dieser Theorie auf Ku­
oben: Ihre Interpretation ist aufschluss­
der Milchstraße entrissen werden.
gelsternhaufen gelingt einfacher als auf
reich. Würden einmal entstandene Haufen
offene Sternhaufen, da der Kontrast zum
nicht zerfallen, so müsste es Sternhaufen
Hintergrund groß und die Mitgliedschaft
geben, die so alt sind wie die galaktische
Der Beitrag offener Sternhaufen
zum Aufbau der Scheibe
leichter bestimmbar ist. Bei offenen
Scheibe (etwa zehn Milliarden Jahre). Dann
Nun schätzen wir ab, wie viele Sterne der
Sternhaufen spielt die Bestimmung der
ließe sich aus der Altersverteilung die Ent­
galaktischen Scheibe sich jemals in einem
Mitgliedschaft die entscheidende Rolle.
stehungsrate der Haufen im Laufe der Zeit
Sternhaufen aufgehalten haben, bevor er
Obwohl der Tycho-2-Katalog keine hohe
direkt ablesen. Dies ist offensichtlich nicht
aufgelöst wurde. Wie die Grafik oben zeigt,
Reichweite besitzt, gelang es uns, die Ge­
so: Ab einem bestimmten Alter nimmt die
erreichen nur wenige Haufen ein Alter
zeitenradien von 236 Haufen zu bestim­
Anzahl der offenen Sternhaufen drastisch
von einer Milliarde Jahren; dagegen kön­
men. Es zeigte sich, dass sie etwa 3,5-mal
ab. Ähnlich wie beim radioaktiven Zerfall
nen Sterne von einer Sonnenmasse und
so groß sind wie die großen Halbachsen
gibt es eine typische Lebenszeit, bei der
weniger um ein Vielfaches älter sein, ohne
der Haufen im Tycho-2-Katalog. Mit die­
die anfängliche Zahl der Haufen um den
dass sie sich merklich verändert haben –
ser Umrechnungsformel konnten wir die
Faktor 1/e = 0,37 abgenommen hat. Unter
die Sterne eines Haufens können dessen
Gezeitenradien aller 650 Haufen unserer
Annahme einer konstanten Bildungsrate
Auflösung bei Weitem überleben.
Liste ableiten.
der Haufen lassen sich aus dem Verlauf
Um den Beitrag der offenen Haufen zur
Aus den Gezeitenradien lässt sich die
der Kurve sowohl diese Bildungsrate als
galaktischen Scheibe abzuschätzen, müs­
Masse der Sternhaufen abschätzen. Derart
auch die typische Lebenszeit ableiten. Die
sen wir das Produkt aus der Bildungsrate
bestimmte Massenwerte werden »Gezei­
Rechnung ergibt, dass sich im Bereich bis
der Haufen mit ihrer mittleren Anfangs­
tenmassen« genannt. Der Gezeitenradius
1000 Parsec um die Sonne im Mittel 1,25
masse über das Alter der Scheibe aufsum­
ist ja dadurch gegeben, dass sich in diesem
Haufen pro Million Jahre bilden, ihre mitt­
mieren. Wie oben beschrieben, beträgt die
Abstand vom Zentrum des Haufens die
lere Lebensdauer beträgt 330 Millionen
Bildungsrate im Umkreis von 1000 Parsec
Gravitationskräfte von Haufen und Milch­
Jahre. Bezogen auf das Alter der Scheibe
um die Sonne 1,25 Haufen pro Million Jah­
straße gerade aufheben. Kennt man die
erleben wir damit heute die 30. bis 40. Ge­
re und ihre mittlere Anfangsmasse 4500
Gravitationswirkung der Milchstraße am
neration der offenen Sternhaufen.
Sonnenmassen. Da die Milchstraßenschei­
Mond-System: Der Mond befindet sich
40
August 2011
lieren die offenen Sternhaufen während
ihres Lebens stark an Masse. Die jüngsten
Sterne und Weltraum
78
IHR SKYWATCHER PARTNER IN ÖSTERREICH
langlebigen, gravitativ gebundenen of­
gleich zu ihrem Durchmesser sehr dünn
fenen Sternhaufen werden.
ist, gehen wir die Frage zweidimensional
Und warum sind eingebettete Haufen
an. Der Wert von 1,25 übersetzt sich damit
mit mehr als 3000 Sonnenmassen so sel­
in 0,4 Haufen pro Quadratparsec und Mil­
ten? Diese Frage haben Pavel Kroupa und
lion Jahre. Nun benötigen wir nur noch
Chris Boily schon 2002 beantwortet: In
das Alter der Scheibe. Sie ist die jüngste
Sternhaufen mit 3000 Sonnenmassen und
Komponente der Galaxis, ihre ältesten
mehr bilden sich viele O- und B-Sterne, die
Sterne sind etwa zehn Milliarden Jahre
ihre Umgebung mit ihren Winden schnell
alt. Damit liefert die oben beschriebene
von Gas und Staub reinigen. NGC 3603
Rechnung für den Beitrag aller jemals ge­
ist hierfür ein gutes Beispiel. Die Chance,
bildeten offenen Sternhaufen zur Massen­
einen massereichen jungen Sternhaufen
dichte der Scheibe den Wert von 18 Son-
zu entdecken, in dem die O- und B-Sterne
nenmassen pro Quadratparsec.
ihre Umgebung noch nicht freigefegt ha­
Aus der Analyse der Sternbewegungen
ben, ist sehr gering. Wenn andererseits in
senkrecht zur galaktischen Scheibe konn­
einem massearmen eingebetteten Haufen
ten die Astronomen Johan Holmberg und
ein massereicher Stern entsteht, so bläst er
Chris Flynn 2004 die gesamte Massendich­
nicht nur Gas und Staub hinweg, sondern
te der Scheibe (Gas, Staub und Sterne) am
auch gleich den ganzen kleinen Haufen
Ort der Sonne bestimmen. Für die Sterne
auseinander. Auf diese Weise kommen
allein ergaben sich 35 Sonnenmassen
die restlichen 60 Prozent der Masse der
pro Quadratparsec. Aber die meisten der
galaktischen Scheibe zu Stande. So könnte
jemals in der Milchstraße gebildeten mas­
es der Sonne also auch ergangen sein. WIEN OPERNGASSE 23.
+43 699 1197 0808
[email protected]
LINZ GÄRTNERSTR. 16.
+43 676 5457 994
[email protected]
BERATUNG, SERVICE, VERKAUF.
WIR LIEFERN WELTWEIT!
NEU GEMINI G53F
5290€
STEREOSKOPISCHES BILD
be, in der sich die Haufen bilden, im Ver­
5290€
PULSAR-2
STEUERUNG
1190€
sereichen Sterne sind inzwischen schon
vergangen und haben einen Großteil ihrer
Masse in Form von Gas und Staub wieder
an die Scheibe abgegeben. Daraus sind be­
reits mehrfach wieder Sterne entstanden.
Wenn wir dies berücksichtigen, ergibt sich,
samt 48 Sonnenmassen pro Quadratpar­
249€
sec in Form von Sternen gebildet wurden.
249€
Demnach haben die offenen Sternhaufen
erforschen am Astronomischen Recheninsti-
jeden anderen Stern gilt also, dass sie mit
tut, Zentrum für Astronomie der Universität
40 Prozent Wahrscheinlichkeit in einem –
Heidelberg die offenen Sternhaufen und ihre
inzwischen längst aufgelösten – offenen
Rolle bei der Entwicklung unserer Galaxis.
SPLER
OKULARE
76€
Sternhaufen entstanden ist.
Prozent der Sterne der Scheibe? Die Beob­
Literaturhinweise
achtungen zeigen immer deutlicher, dass
Bastian, U.: Hipparcos, die wissenschaftliche Ernte beginnt. In: Sterne und
Weltraum 11/1997, S. 938-941
Burbidge, G.: Fred Hoyle – Astrophysiker,
Kosmologe, Querdenker. In: Sterne und
Weltraum 1/2003, S. 26-31
Lada, C., Lada, E.: Embedded Clusters in
Molecular Clouds. In: Annual Review of
Astronomy and Astrophysics 41, 2003,
S. 57-115
Pfau, W.: Streifzüge im HertzsprungRussell-Diagramm. Teil 1 in: Sterne und
Weltraum 6/2006, S. 32–40, Teil 2 in:
Sterne und Weltraum 11/2006, S. 45-52
Sterne nur selten allein entstehen – dem­
nach stammen diese 60 Prozent aller
Sterne vermutlich aus den 90 Prozent aller
eingebetteten Sternhaufen, die das Kin­
desalter nicht überleben.
So schließt sich der Kreis, der bei
den eingebetteten offenen Sternhaufen
begann. Die Massenfunktionen der ein­
gebetteten und der jungen offenen Stern­
haufen haben die gleiche Gestalt. Aber
während man kaum eingebettete Stern­
haufen mit mehr als 3000 Sonnenmassen
findet, gibt es umgekehrt eigentlich zu
wenige junge offene Haufen mit weniger
als 3000 Sonnenmassen. Daraus folgt, dass
massearme eingebettete Haufen schnell
Weitere Literatur im Internet:
www.astronomie-heute.de/
artikel/1114729
OPTIMIERT FÜR SKYWATCHER
Und woher kommen die übrigen 60
3MM, 5MM, 6MM, 9MM,
12MM, 14MM, 18MM
Siegfried Röser und Elena Schilbach
masse beigetragen. Für die Sonne wie für
URSAMINOR
STEUERUNG
BLUETOOTH
AB 99 €
USB+DSLR
AB 87 €
SOFTWARE
AB 29 €
LACERTA
EQHC
HANDBOX
89€
Mit Autoguider
Eingang
FÜR EQ3, EQ5, VIXEN-GP,
ASTRO5 UND ANDERE
STEUERUNGEN
18/48 oder rund 40 Prozent zur Gesamt­
zerfallen und nicht zu vergleichsweise
www.astronomie-heute.de
August 2011 41
WWW.TELESKOP–AUSTRIA.COM
STEREOSKOPISCHES BILD
LACERTA OFF AXIS GUIDER
dass in der galaktischen Scheibe insge­
Diese Version der Praktikumsanleitung wurde 2004-2008 von Thorsten
Nagel erstellt und wird seit 2016 von Cornelia Heinitz weitergeführt.
Grundlage waren die früheren Anleitungen zum Versuch CCD-Kamera
aus dem Fortgeschrittenenpraktikum Experimentalphysik von Jörn Wilms,
Stefan Dreizler, Ralf Geckeler und Martin Bässgen, Kommentare von Jochen Deetjen, sowie die Staatsexamensarbeit von Margit Haberreiter. Ihnen allen sei für diese Vorarbeiten gedankt.