Aufgabe 4.3: Schalten einer induktiven Last Das Beispiel betrifft das

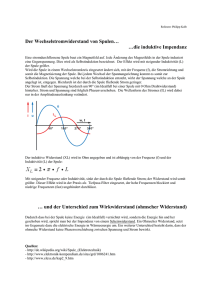
Aufgabe 4.3: Schalten einer induktiven Last
Das Beispiel betrifft das Schalten einer induktiven Last z.B. eines Motors, eines
Elektromagneten, eines Relais oder dergleichen.
Induktive Last
iL(t)
uL(t)
L
R
RL
D
T
U0
»
L
uS(t)
uRL(t)
R
uR(t)
U0
RL
D
S
Fig. 1: Schalten einer induktiven Last L mit einem Transistor T (links). Die Berechnung kann anhand
eines Ersatzbildes erfolgen, in dem der Transistor durch einen Schalter ersetzt wird.
Fig. 1 zeigt ein entsprechendes Schaltbild. Hier wird als induktive Last ein Spule, welche
durch eine Induktivität L und einen, die unvermeidlichen Verluste repräsentierenden,
ohmschen Serienwiderstand R modelliert wird, über einen Transistor T geschaltet. Ein
Transistor im Schalterbetrieb kann in guter Näherung als Schalter betrachtet werden, welcher
über seine so genannte Basis (das ist der im Bild nach links weggehende Anschluss) gesteuert
wird. Bei genügend Basispotential schaltet die so genannte Kollektor-Emitter-Strecke (das ist
die Strecke zwischen den beiden übrigen Anschlüssen) durch und kann durch einen
Kurzschluss ersetzt werden; bei verschwindendem Basispotential kann hier eine
Unterbrechung angenommen werden. Dementsprechend können wir näherungsweise das
rechts im Bild gezeigte Ersatzbild verwenden, wobei der Schalter S hier durch das
Basispotential des Transistors gesteuert wird1. Die beiden noch nicht erwähnten Bauelemente
sind eine Diode D und ein weiterer Widerstand R deren Bedeutung uns in weiterer Folge klar
werden wird. Nehmen wir vorerst an, dass dieser zusätzliche Zweig R-D nicht vorhanden
wäre – er spielt ja beim Schließen des Schalters für unsere induktive Last zunächst auch keine
Rolle. Die ganze Schaltung liegt an einer Gleichspannungsquelle mit dem konstanten Wert
U0.
Nehmen wir an, S wird zu t = 0 geschlossen und die Induktivität möge zu diesem Zeitpunkt
stromlos sein. Die Spannung U0 liegt ab diesem Zeitpunkt an der Serienschaltung RL-L. Das
Aufstellen der Differentialgleichung für diesen Zweig und die Lösung nach den in den
vergangenen Kapiteln beschriebenen liefert nach Berücksichtigung der Anfangsbedingungen
i (t ) 

U0
1  et / 
RL
u L (t )  U 0 e  t / 

1

(1)
L
RL
Neben dieser Anwendung werden Transistoren meist als Verstärker verwendet, hier liegen die Basispotentiale
in einem mittleren Bereich an, wodurch der Strom zwischen Kollektor und Emitter auch effizient „stufenlos“
gesteuert werden kann – mehr dazu in Ihren Elektronik-Vorlesungen.
Wenn der Schalter unendlich lange geschlossen bliebe, würde sich der Strom dem Endwert
U 0 / RL beliebig nähern. (Überlegen Sie sich zur Übung, was im Falle einer idealen Spule mit
RL = 0 passieren würde.) Was passiert nun, wenn der Schalter zu einem Zeitpunkt t1 geöffnet
wird? Da wir vorläufig davon ausgehen, dass der Zweit R-D nicht vorhanden wäre, haben wir
aufgrund des offenen Schalters automatisch die Bedingung i(t )  0, für t  t1 . Die
Induktivität führt allerdings unmittelbar vor dem Öffnen einen endlichen Strom
i (t1 ) 


U0
1  e  t1 /  .
RL
(2)
Da gemäß Stetigkeitsbedingung der Strom in einer Induktivität nicht springen kann, stehen
die beiden Bedingungen miteinander in Widerspruch, welche stimmt also? Tatsächlich kann
die Induktivität den Strom aufrechterhalten, sie erhöht bei „drohendem“ Abreißen des
Stromes nämlich die Spannung an ihren Enden solange, bis der Strom weiter fließt, er bleibt
tatsächlich stetig. Im Falle eines mechanischen Schalters bedeutet dies, dass sich die
Spannung über dem offenen Schalter auf einen Wert steigert, der zur Zündung eines
Lichtbogens führt, welcher den Stromfluss aufrechterhält. Im Falle des Transistors bewirkt die
ansteigende Spannung einen so genannten Durchbruch im Halbleiter, welcher den Transistor
wieder leitend macht – leider ist dieser Effekt jedoch irreversibel, der Transistor ist defekt.
Lichtbögen in mechanischen Schaltern sind mit Materialabtrag verbunden und schädigen den
Schalter auf lange Sicht. In jedem Fall ist man daher bemüht, diesen schädlichen Effekt der
durch die „Entladung“ der Induktivität entsteht, zu vermeiden. Bevor wir eine mögliche
Gegenmaßnahme vorstellen, möchten wir noch kurz an den physikalischen Hintergrund für
die entstehende hohe Spannung erinnern. Formal wird die Spannung an der Spule durch
L di/dt beschrieben. Eine abrupte Stromänderung würde demnach zu unendlich großen
Spannungen führen, was den beschriebenen Spannungsanstieg rechnerisch erklärt. Die
Verknüpfungsbeziehung beschreibt die Selbstinduktion in der Spule, d.h. die Spannung die
durch den, in der Spule selbst fließenden, zeitlich veränderlichen Strom induziert wird.
Letzterer bewirkt das Magnetfeld in der Spule. Wenn dieses Magnetfeld durch einen sich
rapide verringernden Strom zusammenbricht, also einer starken zeitlichen Änderung
unterworfen ist, entsteht entsprechend dem Faradayschen Induktionsgesetz eine große
induzierte Spannung an den Anschlüssen der Spule, welche für die Stetigkeit des Stromflusses
in der Spule gemäß Stetigkeitsbedingung sorgt.
Das bis jetzt ignorierte Glied R-D bietet nun eine Abhilfe. Eine Diode D ist nämlich ein
elektrisches Ventil, das den Strom nur in einer Richtung leitet. Für Ströme in Richtung des
Pfeilsymbols stellt die Diode in guter Näherung einen Kurzschluss dar, andernfalls kann die
Diode als Leerlauf betrachtet werden und eine entgegen der Pfeilrichung im Symbol
orientierte Sperrspannung fällt an ihr ab (verfeinerte Modelle werden Sie in den ElektronikVorlesungen kennen lernen). Bei geschlossenem Schalter S steht über der Diode eine
Spannung in Sperrrichtung, sie leitet nicht und der Strom durch den Serienwiderstand R
verschwindet. Die Sperrspannung an der Diode ist demnach gleich U0. Im parallelen Zweig
RL-L fließt hingegen ein Strom wie oben berechnet. Öffnet der Schalter jetzt zum Zeitpunkt t1,
so muss gemäß Stetigkeitsbedingung der Strom durch die Induktivität weiter fließen und das
ermöglicht ihm die Diode D! Der Stromkreis schließt sich nun nicht mehr über die
Spannungsquelle, sondern über den Zweig R-D so lange, bis die Induktivität entladen ist. Wie
Sie sich leicht ausrechnen können, klingt der Strom gemäß (Sie können die Diode nun durch
einen Kurzschluss ersetzen!)
i (t )  i (t1 ) e (t  t1 ) /  1
mit  1 
(3)
L
RL  R
ab. Die gesamte Spannung an der Spule, uS, ergibt sich aus
u S (t )  u RL (t )  u L (t )  u R (t )  i(t ) R  i(t1 ) R e (t t1 ) /  1 .
(4)
Dementsprechend dreht sich die Richtung der Spannung an der Spule mit dem Öffnen des
Schalters schlagartig um und klingt dann exponentiell (mit einer neuen Zeitkonstante 1) ab!
Die Höhe der Spannungsspitze ist in der praktischen Auslegung wichtig bei der Auswahl des
Schalters bzw. muss R entsprechend dem Schalter dimensioniert werden. Ein kleineres R
bedeutet eine kleinere Spannungspitze, gleichzeitig verlangsamt sich aber auch der
Entladevorgang. Bei der Berechnung der maximal über dem geöffneten Schalter auftretenden
Spannung ist zu beachten, dass sich die Spulenspannung aufgrund der Polaritätsumkehr zur
Betriebsspannung addiert.
Derartige Schaltungen zur Vermeidung von Spannungsspitzen werden im einfachsten Fall
auch ohne Widerstand R realisiert. In diesem Fall erfolgt der Abbau der Energie während des
Entladevorgangs durch den ohmschen Widerstand der Spule und zum geringeren Teil auch
über die Diode (deren ohmschen Anteil wir hier vernachlässigt haben). Die Diode wird auch
als „Freilaufdiode“ bezeichnet, der Vorgang des Abbaus der in der Spule gespeicherten
magnetischen Energie wurde besonders früher mitunter als „Funkenlöschung“ bezeichnet, da
der Funken (Lichtbogen) am Schalter vermieden wurde.
Fig. 2 zeigt den zeitlichen Verlauf des Stromes und der Spannung an der induktiven Last für
ein Zahlenbeispiel mit L = 100 mH, RL = 50 , R = 200 , U0 = 10 V und t1 = 10 ms.
i(t)
0.2
0.1
0
0
0.005
0.01
t in s
0.015
0.02
0.005
0.01
t in s
0.015
0.02
uS(t)
50
0
-50
0
Fig. 2: Verlauf des Stromes und der Spannung an einer Spule (bestehend aus RL und L) bei Einschalten
und anschließendem Ausschalten unter Verwendung einer Freilaufdiode und eines zusätzlichen
Entladewiderstandes R.