Facharbeit - Haus der Astronomie
Werbung

Facharbeit Spektrographie in der Astronomie Wissenschaftliches Arbeiten mit dem hochauflösenden Gitterspektrographen der Sternwarte Lübeck Leistungskurs Physik Carolin Liefke Astronomie AG der Lauenburgischen Gelehrtenschule Ratzeburg Vorwort zum Vorwort Wenn ich jetzt, gut anderthalb Jahre nach der ersten Version dieser Arbeit, die Originalversion in die Hand nehme, durchblättere und lese, dann fällt mir so einiges auf, was man verändern oder verbessern könnte. Deshalb habe ich mich jetzt zu so etwas wie einer zweiten, verbesserten Auflage entschlossen. Eine stark gekürzte Fassung der alten Fassung hat doch tatsächlich ihren Weg in die Zeitschrift “Sterne und Weltraum” gefunden. Daraufhin wurde ich vom Veranstalter der astrobux, einer Tagung zur Astronomie und Raumfahrt, eingeladen, dort über meine Arbeit zu referieren. Schon vorher hatte ich darüber nachgedacht, die alte Version zu überarbeiten. Beim Zusammenstellen des Materials für den Vortrag bin ich dann auch tatsächlich noch auf kleine Fehler gestoßen, die zuvor niemandem aufgefallen waren. Schließlich wurde ich auf der Tagung auch noch gefragt, ob es möglich wäre, diese Arbeit im Internet zu veröffentlichen. Ich bin von dieser Idee an sich recht begeistert, ein weiterer Grund für eine Überarbeitung. Es mag daran liegen, daß ich jetzt einen anderen Blick auf wissenschaftliches Arbeiten habe, denn ich habe mich entschlossen, die “humorvollen” Passagen von der eigentlichen Arbeit zu trennen, sie finden sich jetzt in kursiv geschriebenen Absätzen. Sie ganz herauszunehmen, das wäre dann doch nicht mein Stil. Ansonsten wurde nur an wenigen Stellen gekürzt, aber an einigen Stellen erweitert, auch was neues Bildmaterial angeht, das ich jetzt unter anderem von den Bauteilen des Spektrographen habe. Desweiteren: Das hier ist LATEX, und ich habe dann doch festgestellt, daß sich LATEX viel leichter c Word, überlisten läßt, das ganze so hinzubekommen wie ich es haben möchte, als Microsoft mit dem die Vorgängerversion erzeugt wurde. Groß Sarau, den 2.4.2003 2 Vorwort Dies ist eine Facharbeit. Meine Facharbeit für den Leistungskurs Physik. Zumindest hauptsächlich und im Moment. Aber hinter diesen Seiten steckt noch viel mehr. Es ist ein Tagebuch. Über mehr als 2 Jahre harter Arbeit. Über viele Tage und Stunden wissenschaftlichen Arbeitens. Tagebuch heißt, daß es ständig weiter geführt wird. Dem Leser kann also in einigen Jahren ein Exemplar über den Weg laufen, dessen Seitenzahl sich vervielfacht hat. Es wird dann natürlich nicht mehr Facharbeit heißen können. Es ist eine Dokumentation. Über jemanden, der sich seit 6 Jahren intensiv mit Astronomie und Physik beschäftigt. Und auch vorhat, das auch den Rest seines Lebens zu tun. Es ist ein Erlebnisbericht. Von den Abenteuern, die man im Umgang mit Spektrographen, CCDKameras, Computern und anderen elektrischen Gerätschaften erleben kann. Das schließt unter c anderem elektrische Schläge und den ewigen Konflikt des Users mit Microsoft Program-men mit ein. Und deshalb auch nicht immer wissenschaftlich trocken wie es eigentlich sein sollte, sondern mit einer Prise meines typischen berichterstattenden Humors versehen. Wer den bereits kennt, wird es verstehen. Alles in Allem ist dies ein großes Dankeschön an alle, die mich während der letzten Jahre unterstützt, ermutigt, und so weiter haben. Groß Sarau, den 23.01.2000 3 many thanks to - Bernd van der Smissen für den wundervollen Spektrographen - Norbert Kordts und Thimo Langbehn deren Programmierfähigkeiten da anfangen wo meine enden - Dieter Kasan ohne den ich wahrscheinlich nie zur Astronomie gekommen wäre - Henrika Liefke für alles 4 Inhaltsverzeichnis 1 Einleitung 1.1 Die Spektrographen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.1.1 Möglichkeiten im Aufbau eines Spektrographen . . . . . . . . . . . 1.1.2 Der Doppelprismenspektrograph . . . . . . . . . . . . . . . . . . . 1.1.3 Der Gitterspektrograph . . . . . . . . . . . . . . . . . . . . . . . . 1.2 Spektrographie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2.1 Grundlagen der Spektrographie . . . . . . . . . . . . . . . . . . . . 1.2.1.1 Das elektromagnetische Spektrum . . . . . . . . . . . . . 1.2.1.2 Die Entstehung von Spektren . . . . . . . . . . . . . . . . 1.2.1.3 Das Bohrsche Atommodell . . . . . . . . . . . . . . . . . 1.2.2 Spektrographie in der Astronomie . . . . . . . . . . . . . . . . . . 1.2.2.1 Sternspektren . . . . . . . . . . . . . . . . . . . . . . . . 1.2.2.2 Sternspektroskopie . . . . . . . . . . . . . . . . . . . . . . 1.2.2.3 Spektralklassifikation und Hertzsprung-Russell-Diagramm 1.2.2.4 Der optische Dopplereffekt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 7 7 12 12 16 16 16 17 18 22 22 22 24 28 2 Übersichtsspektren mit dem Doppelprismenspektrograph 2.1 Aufnahme und Digitalisierung der Spektren . . . . . . . . . . . . . . . . . . . . . 2.2 Weiterverarbeitung und Auswertung . . . . . . . . . . . . . . . . . . . . . . . . . 31 31 32 3 Erste Schritte in der Arbeit mit dem Spektrographen 3.1 Die Lage verschiedener Spektralpunkte . . . . . . . . . . . . . . . . . . . . . . 3.1.1 Auffinden der ersten Spektralpunkte . . . . . . . . . . . . . . . . . . . 3.1.2 Auswertung der Beobachtungen und graphische Darstellung . . . . . . 3.2 Weiterführung der Auswertung . . . . . . . . . . . . . . . . . . . . . . . . . . 3.2.1 Bestimmung der Geradengleichungen . . . . . . . . . . . . . . . . . . . 3.2.2 Berechnung weiterer Spektralpunkte und graphische Darstellung . . . 3.3 Erste Aufnahme von Spektren . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.3.1 Aufnahme von Spektren mit der Photokamera . . . . . . . . . . . . . 3.3.2 Beobachtung von Spektren mit einer einfachen CCD-Kamera . . . . . 3.3.3 Aufnahme von Spektren mit der CCD-Kamera der Sternwarte Lübeck 3.3.4 Auswertung der ersten Spektren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 36 36 38 38 38 38 40 40 40 41 42 . . . . 44 44 44 48 48 4 Die Sonne - unser nächster Stern 4.1 Das Sonnenspektrum . . . . . . . . . . . . . 4.1.1 Die Aufnahme des Sonnenspektrums 4.1.2 Digitale Weiterverarbeitung . . . . . 4.1.3 Auswertung des Spektrums . . . . . 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Ausblick 5.1 Bestimmung von Sonnenrotation und Materiefließgeschwindigkeiten 5.2 Bestimmung der Rotationsgeschwindigkeiten der Planeten . . . . . 5.3 Sternspektren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.4 Untersuchung des “Kordtsschen Doppelsterns” . . . . . . . . . . . 6 Literatur- und Quellenverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 55 56 56 56 57 6 1 Einleitung Zur Einleitung sei nur soviel gesagt: In der siebten Klasse schaffte es mein damaliger Mathematiklehrer Herr Kasan, mich für die Astronomie zu begeistern. Ich trat der von ihm geleiteten Astronomie AG bei, damals wie heute eine Arbeitsgemeinschaft, die ihre Mitglieder eigentlich eher in der Oberstufe sucht. Die AG beschäftigte sich damals unter anderem mit der Sternspektrographie und ihrer praktischen Durchführung. So kam ich damals das erste Mal in Berührung mit der Spektrographie, die Behandlung des Prismas in Physik noch in weiter Ferne. Die Zeit verging, und ich wurde ein erfahrenes Mitglied dieser AG, ich bekam die Möglichkeit mit sehr hochwertigen Geräten zu arbeiten, die Erstklassiges zu leisten vermochten. Die vorliegenden Seiten sollen zeigen, welche Ergebnisse diese Arbeit hervorgebracht hat. Um das auch für Nichtphysiker und Nichtastronomen verständlich zu machen, werde ich auch auf die Grundlagen der Spektrographie, ihre Anwendung in der Astronomie sowie den Aufbau der Spektrographen, mit denen gearbeitet wurde, eingehen. 1.1 Die Spektrographen Mit dem Begriff Spektroskop bezeichnet man ein optisches Gerät, mit dem ankommende elektromagnetische Strahlung mit Hilfe eines dispersiven Elementes in ein Spektrum aufgefächert wird. Im Unterschied zum Spektroskop bietet ein Spektrograph neben der Möglichkeit zur Beobachtung des entstandenen Spektrums auch noch sein lichtelektrisches oder photographisches Erfassen. Die hier erwähnten Geräte verfügen über diese Möglichkeit, ich werde daher der Einfachheit halber immer von Spektrographen sprechen. 1.1.1 Möglichkeiten im Aufbau eines Spektrographen Die Anordnung eines jeden Spektrographen sieht folgendermaßen aus. Die zu spektroskopierende Lichtquelle wird mit einer externen Optik auf einen Spalt fokussiert. Dieser Spalt befindet sich im Brennpunkt einer Kollimatorlinse, so daß hinter der Kollimatorlinse ein paralleles Lichtb ündel entsteht. Eine zweite Linse bildet den Spalt ab, in ihrer Brennebene befindet sich beim Spektrographen die Filmebene. Zwischen die beiden Linsen ist das dispersive Element geschaltet. Weißlicht wird spektral zerlegt, so daß unendlich viele Spaltbilder in unendlich vielen Farben abgebildet werden. Anstelle von Linsen können zur Abbildung des Spaltes auch Spiegel verwendet werden. Das entscheidende Kriterium eines Spektrographen ist das dispersive Element. Prinzipiell gibt es dazu zwei verschiedene Möglichkeiten: Prismen und Gitter (Von Interferometern wird abgesehen.) Die Qualität des Spektrums hängt von zwei grundsätzlichen Faktoren ab. Der erste ist die Dispersion, die räumliche Trennung der Wellenlängen. Der zweite Faktor ist das Auflösungsvermögen, inwieweit zwei benachbarte Linien noch trennbar sind. Ein Prisma ist ein Glaskörper mit nicht parallel liegenden Grenzflächen. Die Zerlegung des weißen Mischlichtes kommt zustande, da das Prisma für jede Spektralfarbe einen anderen Brechungsindex besitzt. Kurze Wellenlängen, also blaues Licht, werden am stärksten abgelenkt, 7 lange Wellenlängen, also rotes Licht, am wenigsten. Daher ist der Maßstab zum blauen Ende hin gedehnt. Prismen weisen im Vergleich zu Gittern nur eine geringe Dispersion auf. Das Auflösungsvermögen eines Prismas beträgt: dn λ = −L (1.1) dλ dλ dλ ist der Abstand zweier gerader noch trennbarer Wellenlängen, L die Basislänge des Prismas und n der Brechungsindex. Abbildung 1.1: Aufbau eines Prismenspektralapparates. Sp Spalt, L 1 Kollimatorlinse, P Prisma, L2 Objektivlinse, S Schirm mit Spaltbildern in Rot (R) und Violett (V). Abbildung aus [ 1 ] Man unterscheidet bei optischen Gittern zwischen Durchsicht- und Reflexionsgitter. Durchsichtgitter beugen das Licht an lichtundurchlässigen Stäben. Es handelt sich meistens um Glasplatten, in die eine Vielzahl feiner Rillen gleicher Breite und gleichen Abstands geritzt werden. Die Rillen wirken wie unendlich viele kleine Spalte, an denen Licht gebeugt wird. Der Abstände der Rillen ist sehr klein. Er wird durch die Gitterkonstante g beschrieben. Übliche Gitter haben 500 Rillen pro mm. Wenn kohärentes paralleles Licht auf das Gitter trifft, breitet es sich nach dem Huygensschen Prinzip in alle Richtungen aus. Die huygenschen Elementarwellen der einzelnen Spalte überlagert sich. Aufgrund der Gangunterschiede zwischen den einzelnen Elementarwellen interferieren sie dabei miteinander und löschen sich entweder gegenseitig aus oder verstärken sich. Beleuchtet man das Gitter mit monochromatischem Licht, beispielsweise mit einem HeliumNeon-Laser, kann man auf einem Schirm das Interferenzmuster beobachten, viele rote Streifen oder Punkte, die alle den selben Abstand haben. Das Licht einer blauen Lichtquelle erzeugt ein ähnliches Muster, die Maxima stehen allerdings enger zusammen. Blaues Licht wird also, im Gegensatz zum Prisma, weniger stark gebeugt als rotes Licht. Eine Lichtquelle mit weißem Licht erzeugt in der Mitte ein weißes Maximum und seitlich in beiden Richtungen mehrere Spektren, die nach außen immer breiter werden. Die Spektren werden vom Maximum in der Mitte nach außen durchnumeriert und mit 1., 2.,3. ... n-ter Ordnung bezeichnet. Der Mittelstreifen ist die 0. Ordnung. Spätere Ordnungen überlagern sich. Die Farben- 8 folge der Spektren ist im Vergleich zum Prismenspektrum genau umgekehrt, da das langwellige Licht die stärkste und das kurzwellige Licht die geringste Ablenkung erfährt. Ein wesentlicher Vorteil des Gitters gegenüber dem Prisma ist, daß das entstandene Spektrum über den gesamten Wellenlängenbereich gleichmäßig ist. Bei einem Reflexionsgitter handelt es sich um eine metallbeschichtete Glasplatte (zumeist mit Aluminium), in die pro mm Breite mehrere hundert parallele Spalten oder Stufen analog zu den Rillen des Durchsichtgitters eingearbeitet sind. Ist das Furchenprofil unsymmetrisch gearbeitet, so spricht man von einem Blazegitter. Den Anstiegswinkel des Profils nennt man entsprechend Blazewinkel Θ. Es kommt durch den Blazewinkel zu einer geometrisch-optischen Reflexion in eine bestimmte Beugungsrichtung. Dadurch wird das eingestrahlte Licht in eine bestimmte Beugungsordnung konzentriert, so daß dort eine gesteigerte Intensität auftritt. Für die Anordnung eines Gitters relativ zum Strahlengang gibt es drei Spezialfälle: 1. Der In-Plane-Mode: Das Gitter steht senkrecht zu der Ebene der einfallenden und ausfallenden Strahlen. Einfalls- und Ausfallswinkel α und β sind nicht gleich. 2. Der Littrow-Mode: Das Gitter steht senkrecht zu der Ebene der einfallenden und ausfallenden Strahlen. Einfalls- und Ausfallswinkel α und β sind gleich, das Gitter reflektiert den einfallenden Strahl in Richtung des Ausfallenden Strahls zurück. 3. Der Off-Plane-Mode: Das Gitter steht nicht senkrecht zu der Ebene der einfallenden und ausfallenden Strahlen. Einfalls- und Ausfallswinkel α und β sind ungleich. Die Neigung des Gitters wird durch den Winkel γ beschrieben. Abbildung 1.2: Interferenz am Reflexionsgitter. Einfallswinkel α, Ausfallswinkel β. Der Gangunterschied ∆x ist die Summe der beiden Teilgangunterschiede ∆x 1 und ∆x2 . Abbildung aus [ 7 ] 9 Abbildung 1.3: Drehung des Gitters um den Winkel γ (Off-Plane-Mode) Abbildung: [ 7 ] Die Effizienz eines Gitters ist im Littrow-Mode maximal. Da ein- und ausfallender Strahl jedoch nicht getrennt sind, würden sich Probleme in der Beobachtung des Spektrums ergeben. Es muß daher auf In-Plane- oder Off-Plane-Mode ausgewichen werden. [ 7 ] Der Zusammenhang zwischen Ordnung n, Wellenlänge λ, Furchenabstand d, Einfallswinkel α, Ausfallswinkel β und Drehwinkel γ eines Gitters wird durch folgende Formel beschrieben: nλ = (sin α + sin β) · cos γ d Die Winkeldispersion bei einer bestimmten Wellenlänge λ ist: dβ n = dλ d · cos β cos γ (1.2) (1.3) Die Lineardispersion (Dispersion des Spektrums in der Filmebene / auf einem Schirm) ergibt sich aus Winkeldispersion und Brennweite f der Kameraoptik zu: dβ dx =f dλ dλ Das Auflösungsvermögen eines Gitters entspricht λ =n·N dλ wobei N die Anzahl der ausgeleuchteten Furchen ist. [ 1 ] 10 (1.4) (1.5) Der Doppelprismenspektrograph Abbildung 1.4: Hochauflösender aber unhandlicher Prismenspektrograph mit zwei Prismen zur Aufnahme von Übersichtsspektren. Präzisionsspalt, Anschluß für Spiegelreflexkamera Der Gitterspektrograph Abbildung 1.5: Reflexionsgitter 1302 Striche pro Millimeter, 25µm Glasfaser als Spalt, Anschluß für Spiegelreflex- und CCD-Kamera. Hohe Dispersion, hohe Auflösung. Aufnahme von Detailspektren, speziell von Dopplerverschiebungen 11 1.1.2 Der Doppelprismenspektrograph Der Doppelprismenspektrograph gehört der Sternwarte Lübeck und stammt aus den siebziger Jahren. Sein Aufbau entspricht Abbildung 1.1, abgesehen davon daß, wie sein Name schon sagt, zwei Prismen als dispersive Elemente hintereinander geschaltet sind. Dispersion und Auflösungsvermögen des Spektrographen werden dadurch wesentlich verbessert. Er eignet sich daher sehr gut zur Aufnahme hochaufgelöster Gesamtspektren. Die Spalteinheit des Spektrographen wurde als selbständige Einheit neu gestaltet. Der neue Spalt ermöglicht eine sehr schmale Spaltbreite und damit wieder eine Steigerung der Qualität der Spektren. Zur Aufnahme der Spektren wird eine Spiegelreflexkamera angeschlossen. Das gesamte Spektrum kann dann in der Filmebene abgebildet werden. Leider ist der Doppelprismenspektrograph für seine Maße sehr schwer und damit unhandlich. 1.1.3 Der Gitterspektrograph Der Gitterspektrograph wurde 1996 von Bernd van der Smissen als Diplomarbeit im Studiengang Physikalische Technik der Fachhochschule Lübeck entworfen und konstruiert und in der Werkstatt der Fachhochschule gebaut. Er hat für diese außergewöhnliche Leistung den zweiten Preis der Possehl-Stiftung erhalten. Der Bau des Spektrographen wurde vom Schulverein der Lauenburgischen Gelehrtenschule finanziert. Die Kosten für das Gitter sowie für den Kollimatorspiegel wurden von Herrn Kasan übernommen. Der Spektrograph wurde speziell zur Messung von Dopplerverschiebungen von astronomischen Objekten konstruiert (⇒ 1.2.2.4). Er soll es der Sternwarte Lübeck ermöglichen, die Geschwindigkeit astronomischer Objekte mit höherer Genauigkeit zu messen, als dies mit dem Doppelprismenspektrographen möglich ist. Bei der Konstruktion des Gerätes wurde zunächst entschieden, den Spektrographen und das Teleskop der Sternwarte nicht direkt miteinander zu verbinden, da das Gerät durch seine große Masse die Montierung belasten würde. Außerdem wäre der Spektrograph damit unabhängig von der Stellung des Teleskops. Um das Licht vom Teleskop zum Spektrographen zu leiten, wird eine Glasfaser verwendet. Eine entsprechende Einkoppelvorrichtung zur Positionierung des Sternes auf die Glasfaser gehört zum Spektrographen dazu. Die Einkoppelvorrichtung wird an den Tubus des Fernrohrs angeschlossen. Mit Hilfe eines Fadenkreuzokulars wird die Glasfaser direkt auf das zu spektrographierende Objekt fokussiert. Die Einkoppelvorrichtung wurde nicht zusammen mit dem Spektrographen sondern erst nachträglich gebaut und stand daher für die ersten spektrographischen Versuche nicht zur Verfügung. Inzwischen ist sie allerdings fertiggestellt. Die Glasfaser hat einen Innendurchmesser von 25 µm und einen Außendurchmesser von 125 µm. Sie leitet das Licht in das Gehäuse des Spektrographen, direkt auf den Kollimatorspiegel. Bei dem Kollimatorspiegel handelt es sich um einen Parabolspiegel mit einer Brennweite von 660 mm und einem Durchmesser von 100 mm. Er richtet das Licht parallel und läßt es auf das Gitter einfallen. Bei dem Gitter handelt es sich um ein Reflexionsgitter mit einer Breite von 60 mm und 1302 Spalten pro mm. Das entspricht einem Furchenabstand von 768 nm. Das Gitter wird im InPlane-Mode betrieben. Das Gitter ist nach dem Blazeverfahren für die 1. Ordnung bei 480 nm und einem Blazewinkel von Θ = 18◦ gearbeitet. Dadurch wird die Intensität auf die -1. Ordnung konzentriert. Theoretisch lassen sich die Ordnungen -3 bis 3 beobachten. Allerdings ist in den beiden 3. Ordnungen die Intensität bereits nicht mehr sehr groß, aber Auflösungsvermögen und Dispersion sind in der 3. Ordnung am größten. 12 Eine Anordnung von zwei Spiegeln, ein Kutterscher Schiefspiegler, fungiert als Objektiv. Vom Gitter aus gelangt das Licht vom Hauptspiegel über den Fangspiegel auf die Filmebene. Der Hauptspiegel hat einen Durchmesser von 60 mm, der Fangspiegel einen Durchmesser von 32 mm. Für die Aufnahme der Spektren gibt es zwei Möglichkeiten: Mittels Photokamera und mittels CCD-Kamera. In der Filmebene ist ein Kameraauszug für die Photokamera angebracht. Natürlich läßt sich in dem Gesichtsfeld der Kamera nur ein kleiner Teil eines Spektrums beobachten. Der Drehwinkel α und damit die Neigung des Gitters läßt sich mit Hilfe einer Skaleneinteilung von 0 bis 999 in einem Bereich von 90 ◦ einstellen. Diese 90◦ beinhalten den Bereich der -1. Ordnung bis zum blauen Bereich der 3. Ordnung. Die 0. Ordnung ist bei Skaleneinteilung 000,0 zu finden, die -1. Ordnung im Bereich von 175 bis 270, die 1. Ordnung von 815 bis 720, die 2. Ordnung von 625 bis 440, der violette Bereich der 3. Ordnung geht von 490 bis 450. Hier überschneiden sich also 2. und 3. Ordnung. Will man sicher gehen, daß man nur eine bestimmte Ordnung beobachtet, muß ein Filter eingesetzt werden. Jeweils bei Zähler 384,6 und 423,1 ist Anschlag. Die unterschiedlichen Drehwinkel für unterschiedliche Ordnungen und Bereiche im Spektrum sorgen dafür, daß sich die Ein- und Ausfallwinkel α und β ständig ändern. Das beeinflußt auch die Anzahl der ausgeleuchteten Furchen auf dem Gitter. Daher müssen Auflösungsvermögen und Dispersion des Gitters für jede Ordnung und Wellenlänge nach den oben genannten Formeln neu berechnet werden. Da kein Spalt vorhanden ist, entsteht kein Linienspektrum. Als Spalt fungiert die Glasfaser, durch deren punktförmigen Querschnitt man ein Spektrum zusammengesetzt aus Punkten erhält. Aus diesem Grund werde ich öfter von Spektralpunkten anstelle von Spektrallinien sprechen. Die scheinbaren Helligkeiten der Sterne wurde schon in der Antike in sechs sogenannte Größenklassen eingeteilt. Die hellsten Sterne gehörten zur ersten Größenklasse, gerade noch mit bloßem Auge erkennbare Sterne gehörten zur sechsten Größenklasse. Später hat man diese empirische Einteilung an eine mathematische Definition angepaßt. Die scheinbare Helligkeit berechnet sich aus der Definition des Helligkeitsunterschieds zweier Sterne zu m1 − m2 = −2, 5 · log S1 S2 (1.6) und wird als Maßeinheit mit Magnitudo mit hochgestelltem m angegeben. Sirius, der hellste Stern des Sternhimmels, erhält so beispielsweise eine scheinbare Helligkeit von −1, m 47. Nach Berechnungen des Diplomanden sollten Sterne bis zur sechsten Größenklasse mit Hilfe der CCD-Kamera der Sternwarte Lübeck zu spektrographieren sein. Eine empfindlichere CCDKamera könnte diese Grenze weiter hinaus schieben. Das Gerät zeugt von einer Qualität, die mit normalen schulischen Mitteln nicht erreicht werden kann. Ein Fachmann schätzte seinen Wert auf einen höheren fünfstelligen Betrag. 13 Abbildung 1.6: Außenansicht An der Vorderseite von links nach rechts: Zählwerk der Skalenteilung mit Drehknopf, ändert über Drehstange die Neigung des Gitters. Halterung und Lustiermöglichkeit des Kollimators. Scharfstellung, verschiebt die Position des Kameraanschlussesnach vorn oder nach hinten. Hinten: Gitter mit Dreheinheit. Nicht sichtbar: Anschluß der Glasfaser. Abbildung 1.7: Innenansicht 14 Kollimator, Schiefspiegler und Kamerauszug Abbildung 1.8: Kollimator (im Hintergrund): Brennweite 660 mm, Durchmesser 100 mm; Hauptspiegel des Schiefspieglers (Vordergrund): Durchmesser 60 mm, links davon der Kameraauszug. Gitter und Dreheinheit Abbildung 1.9: Gitter, durch Drehstange um den Aufhängepunkt links drehbar. Vorne rechts der Fangspiegel des Schiefspieglers, Durchmesser 32 mm 15 1.2 Spektrographie Die Spektroskopie ist die Wissenschaft von der Erzeugung, Beobachtung und Registrierung von Spektren sowie ihrer Auswertung. Da es hier aber hauptsächlich um die Aufnahme der Spektren mit Hilfe von Photo- oder CCD-Kameras geht, werde ich, analog zu den Spektrographen immer von Spektrographie sprechen. 1.2.1 Grundlagen der Spektrographie 1.2.1.1 Das elektromagnetische Spektrum Unter dem Begriff elektromagnetische Strahlung faßt man das sichtbare Licht, die Wärme- oder Infrarotstrahlung, das UV-Licht, die Röntgen- und Gammastrahlung und Radiowellen zusammen. Die verschiedenen Strahlungsarten unterscheiden sich in Wellenlänge und Frequenz voneinander. Mit zunehmender Frequenz werden die Wellenlängen kleiner. Abbildung 1.10: Das elektromagnetische Spektrum mit dem optischen Bereich Das sichtbare Licht in der Farbfolge Rot, Orange, Gelb, Grün, Blau und Violett ist nur ein kleiner Bereich des elektromagnetischen Spektrums. Er umfaßt die Frequenzen von 4 · 10 14 Hz bis 8, 2·1014 Hz. Das entspricht einem Wellenlängenbereich von 780 nm bis 360 nm. Der sichtbare Bereich wird von Infrarotstrahlung und UV-Strahlung begrenzt. Wenn ich von Spektrographie spreche, dann beschränke ich mich auf den optischen Bereich, auf das sichtbare Licht. Natürlich kann auch neben dem sichtbaren Licht in den anderen Spektralbereichen Spektrographie betrieben werden. Das ist allerdings mit einem viel größeren Aufwand verbunden. Hinzu kommt, daß es ja hauptsächlich um die Spektrographie extraterrestrischer Objekte gehen soll. Die Erdatmosphäre absorbiert jedoch einen Großteil der auf sie treffenden elektromagnetischen Strahlen. Nur im optischen Bereich und im Bereich der Radiowellen wird ein Großteil hindurchgelassen. Man spricht vom optischen Fenster und vom Radiofenster. 16 Abbildung 1.11: Absorption elektromagnetischer Wellen durch die Erdatmosphäre [ 9 ] 1.2.1.2 Die Entstehung von Spektren Läßt man weißes Licht auf ein dispersives Element fallen, so wird es in seine einzelnen Farbbereiche zerlegt, ein Spektrum entsteht. Wie genau jedoch das Spektrum aussieht, hängt von der Beschaffenheit des zu untersuchenden Körpers ab. Ein glühender, fester oder flüssiger Körper sowie Gase unter hohem Druck und hoher Temperatur erzeugen ein zusammenhängendes, kontinuierliches Spektrum. Das beste Beispiel für einen Körper, der ein solches Spektrum erzeugt, ist eine Glühbirne. Aber auch das Licht einer Kerzenflamme erzeugt ein kontinuierliches Spektrum. Leuchtende Gase unter geringerem Druck oder niedrigerer Temperatur zeigen einzelne helle Emissionslinien. Die einzelnen Linien sind typisch für das jeweilige Element. Leuchtstoffröhren beispielsweise zeigen ein Emissionsspektrum. Der entgegengesetzte Fall tritt aber auch auf. Beim Absorptionsspektrum ist das kontinuierliche Spektrum von mehreren dunklen Linien unterbrochen. Es entsteht, wenn das Licht eines Körpers, der für sich allein genommen ein kontinuierliches Spektrum erzeugt, durch ein kühleres Gas läuft. Das Gas absorbiert das Licht genau der Wellenlängen, die es im Leuchtzustand emittieren würde, so daß von diesen Wellenlängen weniger Licht beim Beobachter ankommt und die Linien dunkel erscheinen. Jedes Element hat charakteristische Linien im sichtbaren Spektralbereich. Das können sehr wenige sein, wie bei Natrium oder Lithium. Wasserstoff und Helium haben da schon einige mehr. Die Edelgase Neon oder Argon erzeugen bereits ein ganzes Kontingent. Moleküle erzeugen ganze Banden von Linien. Aufgrund der für die Elemente charakteristischen Lage der Linien in Emissions- und Absorptionsspektren kann man durch Spektralanalyse Aussagen über die qualitative Zusammensetzung eines unbekannten Stoffes machen. 17 Abbildung 1.12: Zur Entstehung von Absorptions- und Emissionsspektren. Ein Körper erzeugt ein ursprünglich kontinuierliches Spektrum. Sein Licht durchläuft einen Behälter mit Wasserstoffgas. Ein hinter dem Behälter aufgestellter Spektrograph registriert ein Absorptionsspektrum mit den typischen Wasserstofflinien. Das Gas selbst beginnt zu leuchten. Ein seitlich aufgestellter Spektrograph, der nur das vom Gas kommende Licht registriert, nimmt ein Emissionslinienspektrum auf. Abbildung aus [ 3 ] 1.2.1.3 Das Bohrsche Atommodell Wieso aber erzeugen die einzelnen Elemente diese für sie charakteristischen Linien in den Spektren? Eine Erklärung liefert das Bohrsche Atommodell am Beispiel des Wasserstoffs, dem einfachsten aller Atome. Nach Bohr umkreist das Elektron den Atomkern, das Proton, strahlungsfrei auf klar definierten Bahnen. Normalerweise befindet es sich auf der Bahn, die dem Kern am nächsten ist, dem sogenannten Grundzustand. Dort hat das Elektron die geringste Energie. Um das Elektron auf die nächsthöhere Bahn zu heben, muß dem Atom ein ganz bestimmter Energiebetrag zugeführt werden. Eine Möglichkeit, dem Atom diese Energie zuzuführen, ist die Absorption eines Photons, eines Lichtquants. Die Energie des Lichtquants muß exakt mit der Energie übereinstimmen, die benötigt wird, um das Elektron anzuheben. Ist sie nur geringfügig größer oder kleiner, kann das Photon nicht absorbiert werden. Nach 10 −8 s wird das Elektron von der höheren Bahn in den Grundzustand zurückkehren und dabei ein Photon mit der entsprechenden Energie wieder abstrahlen. Für die Energie eines Photons gilt E = h·ν mit c = ν ·λ. So erklärt sich der Vorgang von Absorption und Emission. Bestrahlt man ein Gas mit weißem Licht, werden die entsprechenden Lichtquanten absorbiert, die benötigt werden, um die Elektronen auf höhere Bahnen zu heben. Das Gas selbst stahlt nur Photonen dieser Energien ab. Das kontinuierliche Spektrum einer Weißlichtquelle weist dann entsprechend dunkle Linien auf, da das Gas die Photonen in alle Richtungen abstrahlt, kommen nur wenige beim Spektrographen an. 18 Für Wasserstoff und wasserstoffähnliche Ionen kann man die Wellenlängen der abgestrahlten Photonen berechnen: 1 me · e 4 · Z 2 = λ 8 · ε 0 · h3 · c 1 1 − 2 2 n m (1.7) Dabei ist me die Masse des Elektrons, e die Elementarladung, 0 die elektrische Feldkonstante, Z die Kernladungszahl, h das Plancksche Wirkungsquantum, n und m sind die Quantenzahlen der jeweiligen Bahnen. Wenn beim Wasserstoffatom Elektronen aus höheren Bahnen in den Grundzustand zurückkehren, entsteht eine Serie von Linien, die man nach ihrem Entdecker Lyman-Serie genannt hat. Der Übergang von der zweiten Bahn in den Grundzustand erzeugt ein Photon mit einer Wellenlänge von 1216 Å, der von der dritten Bahn ein Photon der Wellenlänge 1026 Å, der von der vierten 973 Å und so weiter. Die Photonen der Lyman-Serie sind allerdings so energiereich, daß man die Linien im UV-Bereich des elektromagnetischen Spektrums finden würde und nicht im sichtbaren Bereich. Die Balmer-Serie beinhaltet alle Übergänge höherer Bahnen auf die zweite Bahn. Hier findet man die Linien des Wasserstoffs im sichtbaren Licht. Der Übergang von der dritten auf die zweite Bahn erzeugt ein Photon mit einer Energie, die zu einer Wellenlänge von 6563 Å paßt. Diese Linie liegt im roten Bereich des sichtbaren Lichts, man nennt sie auch Hα. Die zweite Linie, analog Hβ genannt, die zum Übergang der vierten auf die zweite Bahn gehört, liegt mit 4861 Å im blauen Bereich des Spektrums. Linie Nummer 3 oder Hγ hat eine Wellenlänge von 4340 Å. so könnte man diese Liste weiter fortführen. Natürlich gibt es weitere Serien zu den höheren Bahnen. Deren Linien liegen jedoch alle nicht im sichtbaren Bereich. Die Paschen-, Brackett-, Pfund- und Humphries-Serien erzeugen alle Photonen im Infraroten. Ab einer Wellenlänge von 3646 Å bei Übergängen zur zweiten Bahn war das Wasserstoffatom jedoch vorher ionisiert. Das Elektron war also zuvor nicht mehr an den Kern gebunden und konnte jede beliebige Energie haben. Deshalb entstehen ab dieser Ionisationsgrenze keine Linien mehr, sondern ein Kontinuum. Das ist auch die Erklärung für die Entstehung eines kontinuierlichen Spektrums bei glühenden festen oder flüssigen Körpern. Dort sind die Elektronen frei und können beim Einfang beliebige Energien haben. Es gibt aber auch noch die Möglichkeit, daß ein freies Elektron bei einer Begegnung mit einem Atomkern nur abgebremst, aber nicht eingefangen wird. Auch hier wird die Energie in Form eines beliebigen Photons frei. Für die verschieden Arten der Übergänge gibt es spezielle Bezeichnungen. Kontinuumsspektren entstehen entweder bei frei-frei- oder frei-gebunden- Übergängen. Emissionslinien können nur bei gebunden-gebunden-Übergängen entstehen. Die Linien von Wasserstoff und wasserstoffähnlichen Ionen lassen sich noch relativ einfach berechnen. Sobald ein Atom jedoch mehr als ein Elektron besitzt, wird die Berechnung kompliziert, da die Elektronen sich zusätzlich gegenseitig beeinflussen. Die einzelnen Energieniveaus ordnen sich zu dichten Gruppen, sogenannten Termen, mit Unterschieden für die verschiedenen Orbitale. So entstehen ganze Gruppen zusammengehöriger Linien, ein sogenanntes Multiplett. Manchmal einstehen auch Paare oder Dreiergruppen, die man dann als Dubletts und Tripletts bezeichnet. Beispiele für Dublette sind die beiden Natriumlinien bei 5890 Å und 5896 Å und die beiden Linien des einfach ionisierten Calciums bei 3968 Å und 3934 Å. 19 Abbildung 1.13: Modell des Wasserstoffatoms mit Energieniveauschema (Grotian-Diagramm) Abbildung aus [ 3 ] 20 Die Linien eines Ions unterscheiden sich völlig von dem des entsprechenden neutralen Atoms. Mit zunehmender Kernladungszahl werden die entstehenden Linien immer Zahlreicher und das entstehende Spektrum immer komplexer. Bei den Ionen des Eisens beispielsweise sind tausende von Linien bekannt. Noch komplizierter werden die Spektren von Molekülen. Hier beeinflussen sich zusätzlich die Elektronen der einzelnen Atome. Die Linien verschmelzen zu sogenannten Banden. [ 3 ] Abbildung 1.14: Grotian-Diagramm des O + -Ions mit den sichtbaren Übergängen des OIISpektrums. Es entstehen mehrere Multiplette. Der Grundzustand des Ions würde sich in diesem Maßstab etwa 50 cm unter dem Ende dieser Seite befinden. Abbildung aus [ 3 ] 21 1.2.2 Spektrographie in der Astronomie Nahezu das Einzige, was man von den Sternen empfängt, ist ihr Licht. Könnte man aber nichts weiter tun als die Sterne und insbesondere die Sonne nur zu beobachten, wäre das Wissen über die Sterne recht dürftig. Die Spektrographie kann helfen, Fragen nach der Temperatur der Sterne, ihrer Masse, Leuchtkraft, Entfernung und Geschwindigkeit zu beantworten. 1.2.2.1 Sternspektren Die Spektren der Sonne und der meisten Sterne sind Absorptionsspektren. Sterne sind aber keine glühenden festen oder flüssigen Körper, die von einer Schicht kühleren Gases umgeben sind. Die Entstehung der Spektren muß also anders zu erklären sein. Sterne bestehen zu 75% aus Wasserstoff und zu 20% aus Helium. Alle restlichen Elemente machen nur 5% der Sternmasse aus. Das beste Beispiel für einen Stern ist die Sonne. Ihre Energie gewinnt sie durch Kernfusion. Bei Temperaturen von 15 Millionen K im Sonneninnern fusionieren vier Protonen zu einem Heliumkern. Die Massendifferenz wird nach E = mc 2 als Gammaquant entsprechender Energie frei. Auf dem Weg an die Oberfläche muß das energiereiche Photon die Sonne durchqueren. Zunächst erreicht es die Strahlungszone. Hier finden hauptsächlich frei-frei-Übergänge statt, so daß die Energie des Photons langsam abnimmt. Die Strahlungszone geht schließlich in eine Zone der Wärmekonvektion über. Material steigt auf, kühles Material sinkt ab. Das Photon erreicht die Oberfläche der Sonne, die Photosphäre. Auf diesem Weg haben die Photonen einen Großteil ihrer Energie verloren. Für die 696.000 km durch die Sonne, das ständige Absorbieren und Emittieren in der Strahlungszone und die Wärmekonvektion, braucht das Photon insgesamt 10 Millionen Jahre. Für die 149,6 Millionen km von der Sonnenoberfläche zur Erde benötigt das Photon dann nur noch 8 1/2 Minuten. Das sichtbare Licht, daß wir von der Sonne erhalten, stammt aus der Photosphäre. Sie ist bei der Sonne weniger als 200 km dick. Hier müssen die Dinge geschehen, die das Absorptionsspektrum entstehen lassen. In den untersten Photosphärenschichten entsteht zunächst ein kontinuierliches Spektrum. Lange Zeit konnte man sich die Entstehung des kontinuierlichen Photospärenspektrums nicht erklären, da frei-frei-Übergänge Photonen viel zu geringer Energie erzeugen und die normale freigebunden-Strahlung erst ab 3646 Å beginnt. Die Lösung des Problems gelang 1938 R. Wild. Er nahm an, daß das Elektron die Kernladung eines Wasserstoffatoms nach außen unvollständig abschirmt, so daß es möglich ist, daß ein neutrales Wasserstoffatom ein weiteres Elektron an sich binden kann und ein H− -Ion entsteht. Die Bindungsenergie des zweiten Elektrons ist wesentlich geringer als die des ersten. So entsteht durch frei-gebunden- Übergänge das kontinuierliche Photosphärenspektrum. Die Absorptionslinien entstehen in den oberen Randbereichen der Photosphäre und dem Übergang zur Chromosphäre. Die Temperatur ist wesentlich geringer als noch in den unteren Schichten der Photosphäre. Sämtliche in diesen äußeren Schichten vorkommenden Elemente, nicht nur Wasserstoff und Helium, hinterlassen ihre Spuren in Form von Absorptionslinien wie Fingerabdrücke im Spektrum zurück. 1.2.2.2 Sternspektroskopie Ein Stern wie die Sonne verhält sich annähernd wie ein Schwarzer Körper, daß heißt, er befindet sich im thermischen Gleichgewicht und emittiert ebensoviel Strahlung wie er absorbiert. Die Verteilung der abgestrahlten Energie erfolgt nach dem Planckschen Strahlungsgesetz: Man mißt das Intensitätsmaximum der Strahlung des Sternspektrums. Für die Sonne liegt das bei ca. 500 nm. Nach dem Wienschen Verschiebungsgesetz T · λmax = 2, 9 · 10−3 m · K 22 (1.8) Abbildung 1.15: Planck-Kurven für verschiedene Temperaturen. Abbildung: [ 3 ] ergibt sich daraus für die Sonne eine Oberflächentemperatur von 5800 K. Das stimmt gut mit dem Stefan-Boltzmann-Strahlungsgesetz überein. Es besagt, daß der Zusammenhang zwischen der Strahlungsleistung, der Oberflächentemperatur und dem Radius eines Schwarzen Körpers durch die Formel L = 4πR2 · σ · T 4 (1.9) beschrieben ist. σ ist die Stefan-Boltzmann-Konstante. Mit einem Wert von 3, 82·10 26 W/m2 für die Strahlungsleistung L der Sonne erhält man daraus eine Oberflächentemperatur von 5770 K, die sogenannte Effektivtemperatur. Diese Rechnungen lassen sich für jeden Stern durchführen. Man kann die Absorptionslinien in den Spektren der Sterne bestimmten Elementen zuweisen und somit Aussagen über das Vorkommen von Elementen in den Sternen machen. Allerdings läßt sich allein aus den einzelnen Linien nur das Vorhandensein eines Elements nachweisen, nicht aber seine Häufigkeit. Der Unbedarfte würde allein aus der Stärke der Linien auf die Häufigkeit eines Elements schließen. Die stärksten Linien im Sonnenspektrum zeigt aber nicht das häufigste Element Wasserstoff sondern einfach ionisiertes Calcium. Auch die Linien des Natrium sind recht auffällig im Sonnenspektrum. Wie kann das sein, zumal wenn man sich erinnert, daß nach dem Bohrschen Atommodell die Energien für die absorbierten Photonen klar definiert sind, die Linien also unendlich schmal sein sollten? Die Heisenbergsche Unschärferelation gestattet den Energieniveaus eine gewissen natürliche Unschärfe. Die natürliche Breite eine Spektrallinie beträgt 1, 2 · 10−5 nm. Hinzu kommt, daß mehrere Effekte den Absorptionsvorgang beeinträchtigen. Findet der Übergang beispielsweise während der Begegnung mit einem zweiten Atom statt, stören sich die elektrischen Felder der Atome, die Linie wird durch Druckverbreitrung unscharf. Diesen Effekt nennt man auch Stoßdämpfung. Ein weiterer Effekt kommt durch die Molekularbewegung der Atome zustande, die mit steigender Temperatur immer größer wird. Bewegt sich das Atom gerade während des Übergangs auf uns zu oder von uns weg, wird die Linie durch den Dopplereffekt verbreitert (⇒ 1.2.2.4). Das alles führt dazu, daß bestimmte Linien bei bestimmten Temperaturen ihre größte Breite erreichen und das Element Calcium die stärksten Linien im Sonnenspektrum zeigt obwohl es in der Häufigkeit erst an 14. Stelle kommt. Hätte die Sonne eine Oberflächentemperatur von 10000 K, so währen die Linien die Balmer-Serie des Wasserstoffs die stärksten Linien im Sonnenspektrum. Weiß man um die Abhängigkeit der Linienstärken von der Oberflächentemperatur, kann man unter der Annahme, daß die äußeren Schichten der Sterne dieselbe Zusammensetzung wie die 23 Abbildung 1.16: Linienstärken in Sternspektren in Abhängigkeit von der Oberflächentemperatur des Sterns. Abbildung aus [ 3 ] Sterne insgesamt aufweisen, auch die relativen Häufigkeiten einzelner Elemente bestimmen. Die Stärke einer Absorptionslinie zeigt sich durch ihre Breite und ihre Tiefe, also wie dunkel die Linie erscheint. Zum Vergleich zweier Linien benutzt man die sogenannte Äquivalentbreite. Man versteht darunter die Breite eines rechteckigen Absorptionsstreifens mit der Intensität Null, dessen Fläche gleich der von der Kontur der betrachteten Spektralinie begrenzten Fläche ist. Abbildung 1.17: Zur Definition der Äquivalentbreite. Abbildung aus [ 6 ] 1.2.2.3 Spektralklassifikation und Hertzsprung-Russell-Diagramm Schon früh hat man versucht, die Sterne nach Charakteristika in ihren Spektren zu ordnen. Das nennt man Spektralklassifikation. Als bester Anhaltspunkt bot sich dafür natürlich die Stärke bestimmter Linien, insbesondere der des Wasserstoffs. Das geschah erstmalig 1890, lange bevor man um den Zusammenhang zwischen Temperatur und Linienbreite wußte. Man ordnete den Sternen mit den breitesten Wasserstofflinien im Spektrum den Buchstaben A zu, den nächst 24 schmaleren den Buchstaben B und so weiter. Es stellte sich jedoch schnell heraus, daß einige der festgelegten Spektralklassen identisch waren oder auf Fehlern in den Photoplatten beruhten. Eine Aufräumaktion im Buchstabensystem beseitigte die Klassen C, D,E, H, I und L. Übrig blieben A, B, F, G, K, M und O. Später begann man diese Klassen weiter zu unterteilen, indem man eine Dezimalunterteilung einführte. Außerdem erkannte man aufgrund des Vorhandenseins bestimmter Linien in den Spektren, daß die Klassen O und B eigentlich vor der Klasse A stehen müßten. So hatte man die Spektralsequenz unbewußt in die richtige Reihenfolge f ür eine Temperatursequenz gebracht. Die Reihenfolge der Buchstaben OBAFGKM mit den neu eingef ührten Sondergruppen R,N und S lernt der Anfänger in der Astronomie am besten mit dem Merksätzchen: Oh be a fine girl/guy, kiss me right now, smack! Am Anfang der Spektralklassifikation stehen die O-Sterne. Es sind die heißesten Sterne mit Oberflächentemperaturen von bis zu 50000 K. Aufgrund ihrer hohen Temperatur erscheinen diese Sterne bläulich am Himmel. Sie sind nicht nur die heißesten und blauesten, sondern auch die hellsten und massereichsten Sterne. Außerdem sind sie sehr selten. Ihre Spektren zeigen neben der Balmer-Serie des Wasserstoffs hauptsächlich Linien des Helium. Von den anderen Spektralklassen grenzen sie sich durch das häufige Auftreten von Emissionslinien ab. Es folgen die B-Sterne, sie sind ein wenig kühler. Ihre Temperatur reicht von 10000 K bis 30000 K, die Wasserstofflinien werden stärker. Die B-Sterne stellen den Großteil der hellen Sterne am Himmel. Spica und Regulus gehören ebenso wie die hellsten Sterne der Plejaden zu den B-Sternen. Bei den A-Sternen findet man die stärksten und auffälligsten Wasserstofflinien. Die Sterne erscheinen wegen ihrer Temperatur von etwa 8000 K weiß. Der hellste Stern des Sternenhimmels, Sirius, ist ein A-Stern. Auch die Wega in der Leier und Atair im Adler zählen zu den A-Sternen. Mit den F- und G-Sternen kommen wir in den Bereich unserer Sonne. Sie ist ein G2-Stern. Die Linien H und K des einfach ionisierten Calciums beginnen auffällig zu werden, die ersten Molekülbanden und Metallinien treten auf. Die G-Sterne haben Temperaturen von 5000 bis 6000 K, die F-Sterne liegen darüber. Daher haben sie eine weißgelbe bis orangene Farbe. Helle Sterne wie Procyon und Capella gehören zu den F- und G-Sternen. Die Spektralklassen K und M repräsentieren die kühlen, orangenen und roten Sterne. Ihre Oberflächentemperaturen gehen dabei hinunter bis auf 2000 K. Die Spektren werden von Molek ülbanden und Metallinien dominiert. Die Balmer-Serie ist fast verschwunden. Die Spektralsequenz beginnt also mit hohen und endet mit tiefen Temperaturen. Je nach Temperatur werden die Spektren von bestimmten Linien dominiert. Bei den heißen Sternen finden sich Emissionslinien, mit abnehmender Temperatur dominiert die Balmer-Serie des Wasserstoffs. Nimmt die Temperatur noch weiter ab, kommen die Linien verschiedener Metalle wie Calcium und Eisen hinzu. Zum Ende der Spektralsequenz kann man bei den niedrigsten Temperaturen häufig Molekülbanden wie von Titanoxid finden. In den Jahren 1911-13 entwickelten unabhängig Ejnar Hertzsprung und Henry Noris Russell unabhängig voneinander das nach ihnen benannte Hertzsprung-Russell-Diagramm. Die Oberflächentemperatur eines Sterns nach der Spektralklasse wird dabei gegen seine Leuchtkraft oder absolute Helligkeit aufgetragen. Die Temperatursequenz beginnt mit den hohen Temperaturen und nimmt dann ab. Das Hertzsprung-Russell-Diagramm zeigt ein ganz charakteristisches Aussehen. Die meisten Sterne befinden sich auf einer geraden Linie, der sogenannten Hauptreihe. Der Verdienst von Hertzsprung und Russell ist es, daß sie herausfanden, das sich weitere Sterne in Gruppen anordnen. Streng getrennt von der Hauptreihe etwas oberhalb davon befinden sich die Riesen und Überriesen. Unter der Hauptreihe ordnen sich die sogenannten Weißen Zwerge an. Was bedeutet das für diese Sterne? Die Hauptreihe läßt sich relativ einfach erklären: Sterne mit 25 Abbildung 1.18: Die Spektralklassen mit repräsentativen Spektren. Abbildung aus [ 2 ] einer geringen Temperatur haben auch nur eine geringe Leuchtkraft, Sterne mit hoher Temperatur haben eine hohe Leuchtkraft. Wenn man bedenkt, das die Leuchtkraft mit der Masse zusammenhängt, so ordnen sich auf der Hauptreihe links oben große und heiße Sterne an, rechts unten findet man kleine, kühle Sterne. Die Riesen und Überriesen fallen dadurch auf, daß sie für ihre Temperatur sehr große Leuchtkräfte aufweisen. Die Weißen Zwerge dagegen haben eine recht hohe Temperatur, sind aber sehr dunkel. Wenn man die Sterne der Sonnenumgebung in das Hertzsprung-Russell-Diagramm einordnet, findet man die Sonne in der Mitte auf der Hauptreihe. In ihrer Nähe und ebenfalls auf der Hauptreihe tummeln sich Sirius, die Wega und Regulus, der Hauptstern des Sternbildes Löwe. Aber auch unter den Riesen findet man bekannte Sterne. Capella, der Hauptstern des Fuhrmanns, ist ein G2-Stern wie unsere Sonne, seine Leuchtkraft ist jedoch wesentlich größer. Ebenso finden sich bei den Riesen Aldebaran und Pollux. Zu den Überriesen zählt man die rote Beteigeuze und Antares, den Skorpionstern. Unter den Weißen Zwergen findet sich der Begleiter des Sirius wieder. Sterne können also die gleiche Spektralklasse haben, aber dennoch unterschiedliche Leuchtkräfte, wie beispielsweise unsere Sonne und Capella im Fuhrmann. Deshalb hat man die Sterne zusätzlich zu den Spektralklassen in Leuchtkraftklassen mit römischen Zahlen eingeordnet. Der Leuchtkraftklasse I gehören die Überriesen an, der Klasse II die hellen Riesensterne, der Klasse III die normalen Riesen. Die Leuchtkraftklasse IV gehört den sogenannten Unterriesen. Die Sterne der Hauptreihe und damit unsere Sonne gehören zur Leuchtkraftklasse V. Die Weißen Zwerge und die sogenannten Unterzwerge machen die Leuchtkraftklassen VI und VII aus. 26 Abbildung 1.19: Hertzsprung-Russell-Diagramm mit der Lage bekannter und heller Sterne. Abbildung aus [ 3 ] 27 Im Laufe seines Lebens verändert sich die Position eines Sterns im Hertzsprung-Russell-Diagramm. Früher nahmen die Astronomen an, die Sterne wurden im Laufe ihres Lebens die Hauptreihe entlangwandern. Sie würden ihr Leben als heiße O-Sterne beginnen, im Laufe ihres Lebens abkühlen und als kalte M-Sterne enden. Heute weiß man, daß das nicht so ist. Die Lage eines Sterns auf der Hauptreihe ist einzig und allein abhängig von seiner Masse. Die Sterne unterschiedlicher Masse haben unterschiedliche Lebenswege und auch eine unterschiedliche Lebensdauer. Ein Stern mit einem vielfachen der Sonnenmasse verbraucht seinen Brennstoffvorrat viel schneller als ein Stern mit einer halben Sonnenmasse. Unsere Sonne wird ein Alter von etwa 10 Milliarden Jahren erreichen, die Hälfte davon hat sie bereits hinter sich. Sehr massereiche Sterne dagegen werden manchmal nur einige Millionen Jahre alt, die kleinen M-Sterne können mehr als doppelt so alt als unsere Sonne werden. Sterne bilden sich aus Staub- und Gasnebeln, die sich zusammenziehen. Dabei steigt in ihrem Inneren der Druck und mit ihm die Temperatur. Sobald eine bestimmte Temperatur erreicht ist, startet im Innern des Sterns die Kernfusion, der Stern ist geboren und er tritt in die Hauptreihe ein. Hier verbleibt er die meiste Zeit seines Lebens, an welcher Stelle hängt nur von der Masse des Sterns ab. Wenn sich sein Leben dem Ende nähert, beginnt der Stern im HertzsprungRussell-Diagramm zu wandern. Wenn sich sein Brennstoffvorrat erschöpft, beginnt der Stern, sich aufzublähen und extrem leuchtkräftig zu werden. Mit der Expansion kühlt der Stern gleichzeitig ab. Der Stern ist innerhalb kürzester Zeit zu einem Roten Riesen geworden, er hat sich weit nach rechts oben bewegt. in diesem Stadium wird er wiederum je nach Masse verweilen, bis er sein Endstadium erreicht. Bei unserer Sonne wird das ein Weißer Zwerg sein, also ein sehr heißer, kleiner aber leuchtschwacher Stern. 1.2.2.4 Der optische Dopplereffekt Nur wenigen Leuten ist bewußt, daß die meisten Sterne gar nicht allein im Weltall verteilt sind. Oft sind sie in Doppel- oder Mehrfachsystemen angeordnet, das bedeutet, daß zwei oder mehr Sterne einander umkreisen. Das bekannteste, bereits mit bloßem Auge sichtbare Doppelsternpärchen besteht aus Mizar und Alkor, dem Deichselstern des Großen Wagens mit seinem “Reiterlein”. Alkor braucht für einem Umlauf um Mizar etwa 800.000 Jahre. Wenn man Mizar jedoch im Fernrohr betrachtet, erkennt man, daß Mizar selbst noch mal aus zwei Sternen besteht. Sie benötigen für einem Umlauf 3,4 Jahre. Wenn man die Einzelsterne im Fernrohr getrennt beobachten kann, kann man sie nat ürlich auch einzeln spektrographieren. Es kann aber auch vorkommen, daß die Einzelsterne so nahe beieinanderstehen, daß man nur einen Stern erkennt und auch nur ein Spektrum erhält. Doch durch das Spektrum können sich solche Doppelsterne verraten. Während sich die beiden Sterne umeinander bewegen, kommt es vor, daß sich ein Stern zeitweise auf uns zu und dann wieder von uns wegbewegt. Diese Bewegung kann man im Spektrum nachvollziehen, denn die Linien verschieben sich. Die Linien des Spektrums teilen sich in zwei Linien auf, die zu den Einzelsternen gehören. Bewegt sich der Stern auf uns zu, ist die Linie blau verfärbt, bewegt er sich von uns weg, so ist sie rot verfärbt. Etwas ähnliches kann man auch im Alltag beobachten. Hört man einen Rettungswagen auf sich zufahren, scheint die Sirene einen höheren Ton zu haben, als wenn das Fahrzeug sich entfernt. Nach dem österreichischen Physiker Christian Doppler nennt man diesen Effekt den Dopplereffekt. ∆λ ist die Wellenlängenänderung, λ1 die empfangene Wellenlänge und λ0 die Referenzwellenlänge. Die Wellenlängenänderung beim optischen Dopplereffekt berechnet sich, solange v klein gegen c ist, zu: v ∆λ = λ0 c Für sehr große Wellenlängenänderungen ergibt sich durch relativistische Rechnung: 28 (1.10) λ1 = λ0 s 1− 1+ v c v c bzw. 2 λ1 −1 v λ0 = 2 c λ1 +1 (1.11) λ0 Anhand der Stärke der Verschiebung kann man die Geschwindigkeit der einzelnen Komponenten berechnen. Beobachtet man den Doppelstern über einen längeren Zeitraum, stellt man die Umlaufzeit fest, wie lange es dauert bis der Stern sich auf uns zu und dann wieder von uns wegbewegt. Mit Hilfe der Keplerschen Gesetze kann man jetzt die Massen der einzelnen Sterne sowie die Bahnradien der Umlaufbahn berechnen. So hat man herausgefunden, daß die beiden Einzelsterne, aus denen Mizar besteht, noch mal aus zwei weiteren Komponenten zusammengesetzt ist, die einander in 20,5 beziehungsweise 182,3 Tagen umlaufen. Untersucht man das Spektrum der sonnennächsten Sterne, kann man deren Eigenbewegungen gegenüber der Sonne nachweisen. So fand W. Huggins 1868 heraus, daß Sirius, der hellste Stern am Himmel, sich mit einer Geschwindigkeit von 48 km/s von der Erde entfernt. Abbildung 1.20: Negativ der periodischen Linienverschiebungen des spektroskopischen Doppelsterns Mizar im Sternbild Großer Wagen. Abbildung: [ 2 ] Die hellste Galaxie am nördlichen Sternhimmel ist der Andromedanebel mit 3,5 m . Man erkennt sie bereits mit bloßem Auge als verwaschenes Fleckchen am Himmel. Sie weist jedoch höchstwahrscheinlich nicht genügend Flächenhelligkeit auf, um sie mit dem Gitterspektrographen untersuchen zu können. Betrachtet man nicht mehr die Spektren einzelner Sterne sondern ganzer Galaxien, so stellt man fest, daß die Absorptionslinien aller weit entfernten Galaxien rotverschoben sind. Sie scheinen sich also alle von uns wegzubewegen, weiter entfernte Galaxien schneller als nahe. Das fand zuerst der amerikanische Astronom Edwin P. Hubble heraus. Die Kosmologie deutet diese 29 Fluchtbewegung als Ausdehnung des Weltalls. Die Wellenlängenänderung bezeichnet man dann als Rotverschiebung mit dem Buchstaben z. ∆λ (1.12) λ Im Jahr 1963 untersuchte man am Palomar-Observatorium das Spektrum eines 12,8m blauen Sternes, der mit der Radioquelle 3C-273 übereinstimmte. Das Spektrum gab den Astronomen einige Rätsel auf. Es zeigte Emissionslinien, die man jedoch nicht zuordnen konnte. Schließlich entdeckte Maarten Schmidt, daß die Anordnung der Linien auf große Rotverschiebungen zur ückzuführen ist. Man erkannte unter anderem die Linien der Lyman-Serie des Wasserstoffs, soweit rotverschoben, daß sie im sichtbaren Bereich des Spektrums lagen. Die Rotverschiebung betrug z = 0, 158. Danach müßte das Objekt 3000 Millionen Lichtjahre entfernt sein. Es kann also kein Stern sein. Heute glaubt man, daß diese Quasistellaren Objekte (Quasare) die Kerne aktiver Galaxien darstellen. Man kennt heute Objekte, die noch viel größere Rotverschiebungen zeigen. Die am weitesten entfernten Objekte, die man bisher gefunden hat, weisen eine Rotverschiebung von z > 5 auf. z= 30 2 Übersichtsspektren mit dem Doppelprismenspektrograph Die Arbeit mit dem Doppelprismenspektrograph liegt bereits einige Jahre zurück. Ich werde hier kurz die Aufnahme eines Übersichtsspektrums sowie die Digitalisierung und Auswertung beschreiben. 2.1 Aufnahme und Digitalisierung der Spektren Übersichtsspektren werden mit dem Doppelprismenspektrographen und eine Spiegelreflexkamera gewonnen. Der Spektrograph wird dazu am Fernrohr befestigt. Zur Aufnahme wird ein Schwarzweiß-Negativfilm (Ilford FP4 125 ASA) verwendet. Ein Stern ist aufgrund seiner großen Entfernung als Punktlichtquelle zu betrachten. Daher kann der Spektrograph wahlweise auch spaltlos betrieben werden. Mit Hilfe der scheinbaren Drehung der Himmelskugel kann man den Stern durch das Gesichtsfeld des Spektrographen wandern lassen. Man erhält dann wieder ein linienförmiges Spektrum. Die Rotation des Himmelsgewölbes ist jedoch im allgemeinen zu schnell, um eine genügende Schwärzung durch das Spektrum auf dem Film zu erreichen. Daher muß das Fernrohr verzögert auf den Stern nachgeführt werden. Zur späteren Identifizierung der einzelnen Linien im Spektrum kann bei Bedarf gleichzeitig das Licht einer Referenzlichtquelle wie der Quecksilber-Cadmium-Dampflampe eingestrahlt werden. Im Sternspektrum entstehen dann Emissionslinien, mit deren Hilfe die umliegenden Absorptionslinien identifiziert werden. Das so gewonnene Spektrum wird dann digital mit Hilfe eines Registrierphotometers erfaßt. Das entwickelte Negativ des Spektrums wird in einen Diarahmen gefaßt. Mit Hilfe einer von Herrn Kasan konstruierten Vorrichtung wird das Spektrum auf eine Photodiode projiziert. Vor der Diode befindet sich ein schmaler Spalt. Das Spektrum wird nun gleichmäßig über den Spalt gefahren. Die von der Photodiode empfangenen Helligkeitswerte werden über einen Analog/Digitalwandler in einen Computer eingelesen. Die Helligkeitswerte können dann graphisch dargestellt werden. Abbildung 2.1: Schaltplan des Registrierphotometers. Der Projektor ist aus einer Halogenlampe, einem Hohlspiegel, einer Kondensorlinse und einer Objektivlinse zusammengebaut. Der Motor bewegt den Diarahmen gleichmäßig über eine Gewindestange. 31 Die Schwierigkeit whrend der Konstruktion des Registrierphotometers lag in der extremen Gleichmäßigkeit, die praktisch überall benötigt wurde, um die Messung nicht zu verfälschen. So erzeugen beispielsweise Spannungsschwankungen ein wechselnde Helligkeit der Lampe und damit ein sinusförmiges Rauschen im registrierten Spektrum. Es wurden spezielle Netzgeräte benötigt, so daß die Abweichungen der gleichgerichteten Spannung unterhalb der Nachweisgrenze des Photometers lagen. Dementsprechend muß auch der Motor, der das Dia mit dem Spektrum über den Spalt bewegt, gleichmäßig laufen. Eine Ruckelbewegung würde das Spektrum verzerren. 2.2 Weiterverarbeitung und Auswertung Sobald die Helligkeitswerte in den Computer eingelesen sind, kann ein spezielles Computerprogramm die Werte in eine einfache Datei umwandeln. Diese Datei besteht aus nichts weiter als einer Kette von Zahlenwerten, den relativen Helligkeitswerten, die das Photometer registriert hat. c Die Datei läßt sich mit MicrosoftExcel öffnen und weiterverarbeiten. Excel kann die Daten als Diagramm darstellen. In dieser graphischen Darstellung kann man dann einzelne Spektrallinien identifizieren und in ihrer Äquivalentbreite miteinander vergleichen. Wir schreiben Freitag, den 28. Mai 1994. Zufällig hatte ich eine fast belegte DD-Diskette bei mir. Der Speicherplatz reichte aber noch locker aus, um noch zusätzlich eine Datei namens apersei.dat aufzunehmen. Es handelte sich um die digitalisierte Version des Spektrums des Sterns α Persei, der hellste Stern im Sternbild Perseus. Der Stern mit dem klangvollen arabischen Namen Algenib ist ein Überriese vom Spektraltyp F5. Sein Spektrum sollte also sowohl die Linien der Balmer-Serie des Wasserstoffs als auch die beiden Linien des einfach ionisierten Calciums klar zeigen. Mit den Worten “Schau mal, ob du was draus machen kannst” wurde mir die Diskette von ehemaligen LG-Schüler und Astronomie AG-Mitglied Jan Dederichs (heute Diplomphysiker) in die Hand gedrückt. Mit dem festen Vorsatz, bald einen Ausdruck des Graphen in der Hand zu halten, den der Computerbildschirm bei der Registrierung der Daten zeigte, startete ich Excel, damals noch in der Version für Windows 3.11. Bis zu diesem Tage befand sich Excel zwar auf meinem Rechner, hatte aber nichts weiter zu tun als in einem von meinem Vater programmierten Makro die Übersicht über mein Taschengeld zu behalten. Angesichts dessen ist es schon ein Wunder, daß ich es schaffte, die Datei mit Excel zu öffnen und in ein Liniendiagramm zu verwandeln. Am nächsten Tag präsentierte ich stolz meine Ergebnisse. Perfekt war das ganze allerdings nicht und so habe ich im Laufe der letzten Jahre immer wieder an der neuen Datei apersei.xls gefeilt. Es handelt sich um die älteste von mir erstellte Datei, die sich noch heute auf meinem (inzwischen allerdings runderneuerten) Rechner befindet. Seit der Umstellung auf Windows 95 heißt sie alpha persei.xls. Die Bastelei an eben dieser Datei hat mich zum Diagramm-Profi unter Excel gemacht. Einfachen Dingen wie die Formatierung von Datenpunkten, Datenreihe, Diagrammfläche, Achseneinteilung und -beschriftung folgten Tricks wie das Einarbeiten weiterer Linien und die Beschriftung der Datenpunkte der wichtigsten Absorptionslinien mit den Wellenlängenwerten. Trägt man die zugehörigen Wellenlängen gegen eine lineare Skala, zum Beispiel den Abstand zum linken Bildrand, auf, erhält man die Korrekturkurve der Dispersion für das Prisma. Sind genügend klar identifizierte Linien im Spektrum vorhanden, am besten von einer bekannten Referenzlichtquelle mit genügend Linien im gesamten Spektralbereich, läßt sich eine solche Kurve mit beliebiger Genauigkeit polynomial nähern. 32 Übersichtsspektrum α Persei (Algenib) Spektralklasse F5 250 33 relative Intensität 200 H β 4861,32 Å 150 H γ 4340,46 Å 100 H δ 4101,736 Å 50 K Ca II 3933,682 Å H Ca II 3968,492 Å / H ε 3970,076 Å 0 Wellenlänge [ Å ] Abbildung 2.2: Ein Übersichtsspektrum der Sonne, mit dem Doppelprismenspektrographen im Jahre 1994 angefertigt. Aufnahme auf Ilford FP4 Plus. Deutlich sind die BalmerSerie des Wasserstoffs und die Linien H und K des einfach ionisierten Calciums zu erkennen. Die meisten weiteren Linien lassen sich hauptsächlich dem Eisen zuordnen, man kann aber auch zusätzlich Magnesium und Calcium identifizieren. Die hellen Emissionslinien im Spektrum gehören zur Quecksilber-CadmiumDampflampe, deren Licht zur Erleichterung der Identifikation der Absorptionslinien als Referenzlichtquelle eingestrahlt wurde. 34 Lineare Korrektion Doppelprismenspektrograph 180 5790.657 160 5769.596 5460.724 5269.55 5172.698 5085.8221 140 35 Lineare Skala 120 4861.32 4799.914 4678.15 100 4358.343 80 4325.775 4340.46 4260.486 4226.74 60 4101.736 40 4077.83 4046.56 4005.254 3968.492 Polynomiale Näherung 4 3 2 y = -6E-12x + 1E-07x - 0.0011x + 3.9603x - 5599.9 3933.67 20 0 3750 4000 4250 4500 4750 5000 Referenzwellenlänge [ Å ] 5250 5500 5750 6000 3 Erste Schritte in der Arbeit mit dem Spektrographen Seit der Fertigstellung des Spektrographen im August 1997 haben hauptsächlich Herr Kasan und ich mit dem Gerät gearbeitet. Da der Spektrograph zunächst noch völlig neu war und noch niemand länger damit gearbeitet hatte, galt es das Gerät zu erproben. Ich machte mich dazu erst einmal mit der Diplomarbeit vertraut. 3.1 Die Lage verschiedener Spektralpunkte Der Diplomarbeit ist zu entnehmen, unter welchen Drehwinkeln und der damit verbundenen Skaleneinteilung die einzelnen Ordnungen in etwa anzutreffen sind. Daher war es nat ürlich wichtig zu erfahren, bei welcher Skaleneinteilung genau die einzelnen Wellenlängen lagen. [ 4 ] 3.1.1 Auffinden der ersten Spektralpunkte Es lag nahe, den Spektrographen an Emissionslichtquellen zu testen, um so die Lage der einzelnen Emissionspunkte festzustellen. Dazu wurden die Dampflampen und Gasentladungsröhren der Physiksammlung verwendet. Wir begannen unsere Versuche mit der Quecksilber-Cadmium-dampflampe. Zur Beobachtung wurde der Sucher einer Spiegelreflexkamera benutzt. Während ich den Zähler verstellte, beobachtete ich das Gesichtsfeld. Tauchte ein Spektralpunkt auf, notierte Herr Kasan den Zählerwert, bei dem er im Mittelpunkt des Gesichtsfeldes zu stehen schien. Der Spektralpunkt konnte anhand seiner Farbe dann eindeutig einer Wellenlänge der Emissionslinien der Dampflampe zugeordnet werden. Das wurde für jede der vier verfügbaren Ordnungen durchgeführt. Bei weiteren Messungen wurden die Natriumdampflampe und die Helium- und Neon-Gasentladungsröhren verwendet. Später entschlossen wir uns, auch das Gesichtsfeld durch die Spiegelreflexkamera in den einzelnen Ordnungen zu bestimmen. Es wurden jetzt nicht mehr nur der Zahlenwert für die Mitte des Gesichtsfeldes notiert, sondern auch die Randwerte, bei den der Spektralpunkt auftauchte, bzw. verschwand. Die Gesichtsfeldmessungen wurden hauptsächlich mit der Quecksilberdampflampe durchgeführt. So sind teilweise nur Daten eines Mittelwertes vorhanden, teilweise aber auch Daten über das Gesichtsfeld. Die Daten für das Gesichtsfeld gelten allerdings nur für die Photokamera und für das subjektive Empfinden meines Auges, da ich immer der Beobachter war. Hier spielt auch die unterschiedliche Helligkeit der Spektralpunkte eine Rolle. Dabei ergaben sich f ür die verschiedenen Ordnungen folgende Werte: Element Hg Hg Hg Wellenlänge (Å) 4046,56 4077,83 4358,343 Zähler (min) — — 452,8 Zähler (max) — — 457,5 Tabelle 3.1: 3. Ordnung 36 Gesichtsfeld — — 4,7 Zähler (Mittel) 490,8 486,9 454,5 Element Hg Cd Cd Hg Cd Hg Hg Hg Na Na Ne Wellenlänge (Å) 4358,343 4678,15 4799,914 4916,036 5085,822 5460,724 5769,596 5790,657 5889,965 5895,932 6143,062 Zähler (min) 626,9 — — 581,6 — 537,2 512,8 511 — — 483,5 Zähler (max) 632,8 — — 587,5 — 543,1 518,2 516,6 — — 488,8 Gesichtsfeld 5,9 — — 5,9 — 5,9 5,4 5,6 — — 5,3 Zähler (Mittel) 630,2 603,9 593,8 584,2 570,5 540,3 515,7 513,9 505,9 505,6 486,2 Gesichtsfeld 8,7 8,5 — 8,6 — — — — 8,2 8,1 8,3 — — — 8,5 Zähler (Mittel) 826,5 812,7 799,5 789,5 789,8 784,5 783,8 782 765,8 752,9 752,2 748,9 748,2 747,9 729,7 Gesichtsfeld — 8,1 8 — — 7,9 7,8 7,9 8,2 Zähler (Mittel) 177,8 178,5 191,5 205,3 211,4 216 241 255,3 255,5 Tabelle 3.2: 2. Ordnung Element Hg Hg Cd Hg He He Cd Cd Hg Hg Hg He Na Na Ne Wellenlänge (Å) 4077,83 4358,343 4662,352 4916,036 4921,926 5015,878 5085,821 5154,659 5460,724 5769,596 5790,657 5875,623 5889,965 5895,932 6334,428 Zähler (min) 822,1 808,4 — 785,2 — — — — 761,7 749 748 — — — 725,4 Zähler (max) 830,8 816,9 — 793,8 — — — — 769,9 757,1 756,3 — — — 733,9 Tabelle 3.3: 1. Ordnung Element Hg Hg Hg Cd Cd Hg Hg Hg Hg Wellenlänge (Å) 4046,56 4077,83 4358,343 4662,352 4799,914 4916,036 5460,724 5769,596 5790,657 Zähler (min) — 173,9 187,9 — — 212,1 237,2 251,1 251,8 Zähler (max) — 182 195,9 — — 220 245 259 260 Tabelle 3.4: -1. Ordnung 37 3.1.2 Auswertung der Beobachtungen und graphische Darstellung Nachdem die ersten Punkte mit Werten vorhanden waren, zeichnete ich zuerst per Hand einfache Grafiken, die den verschiedenen Wellenlängen und Ordnungen einen Wert der Skaleneinteilung zuzuweisen. Bei jeder Ordnung ergab das Schaubild in etwa eine Gerade. Ein ähnliches Bild ergaben auch die Gesichtsfeldwerte. Sie blieben für die einzelnen Ordnungen in etwa konstant. Es ergaben sich folgende Mittelwerte für das Gesichtsfeld der Spiegelreflexkamera in den einzelnen Ordnungen (Für die 3. Ordnung lag nur ein Wert vor): -1. 1. 2. 3. Ordnung: Ordnung: Ordnung: Ordnung: 7,983 8,414 5,667 4,7 Skalenteile Skalenteile Skalenteile Skalenteile Tabelle 3.5: Gesichtsfelder für die verschiedenen Ordnungen in Skalenteilen Das bedeutete, daß die Wellenlänge linear von der Skalenteilung abhängig ist, die ja wiederum durch den Drehwinkel gegeben ist. Diese Tatsache hat die weitere Arbeit sehr erleichtert. Später habe ich die Werte dann in ein Tabellenblatt von Excel eingegeben und die Daten durch das Programm auswerten lassen. Das entsprechende Diagrammblatt zeigte ebenfalls eindeutig Geraden, wenn auch mit ein paar Abweichungen. 3.2 Weiterführung der Auswertung Natürlich konnte man aus den gewonnenen Daten noch mehr herausholen. Besonders vereinfacht wurde dies dadurch, daß es sich bei den Graphen um Geraden handelte. 3.2.1 Bestimmung der Geradengleichungen Durch die gemessenen Datenreihen für jede Ordnung lassen sich mit Excel verschiedene Trendlinien legen. Für diese Trendlinien kann Excel auch Geradengleichungen aufstellen, die folgendermaßen aussehen: Ordnung -1 1 2 3 b ( Schnittpunkt y-Achse ) 98,171 23519 12145 8274 m ( Steigung ) 22,252 -23,558 -12,367 -8,6157 Tabelle 3.6: Geradengleichungen 3.2.2 Berechnung weiterer Spektralpunkte und graphische Darstellung Mit Hilfe dieser Geradengleichungen war es einfach zu bestimmen, wo man noch unbekannte Punkte finden kann und wo die Idealwerte der beobachteten Punkte liegen. So habe ich einige weitere Spektralpunkte die Werte für die jeweiligen Ordnungen berechnet. Bei diesen Punkten handelt es sich um Linien, die im Sonnenspektrum und im Spektrum der meisten Sterne dominieren. 38 Gemessene Daten 7000 6500 Wellenlänge [ Å ] 6000 5500 5000 4500 4000 0 100 200 300 400 500 600 700 800 900 Skaleneinteilung Abbildung 3.1: Beobachtete Dispersionsrelation des Gitterspektrographen Berechnete Daten 7000 6500 Wellenlänge [ Å ] 6000 5500 5000 4500 4000 0 100 200 300 400 500 600 700 800 Skaleneinteilung Abbildung 3.2: Berechnete Dispersionsrelation des Gitterspektrographen 39 900 Element Ca Ca He Hδ Hγ Hβ Na Na Hα Wellenlänge [ Å ] 3933,682 3968,492 3970,076 4101,748 4340,475 4861,342 5889,934 5895,940 6562,808 -1. Ordnung 176,734 173,931 174,003 179,919 190,648 214,558 260,281 260,505 290,519 1. Ordnung 831,366 829,888 829,821 824,232 814,098 791,988 748,326 748,071 719,764 2. Ordnung 663,970 661,155 661,027 650,380 631,077 588,959 505,787 505,301 451,378 3. Ordnung 503,768 499,728 499,544 484,293 456,553 — — — — Tabelle 3.7: Theoretische Skalenteile für wichtige Spektrallinien Eine Überprüfung der gemessenen Punkte ergab außerdem, daß sämtliche Abweichungen von der Geraden auf Zuordnungsfehlern beruhten. So waren bei Helium und Neon den Skalenteilwerten die falschen Linien zugeordnet worden. Eine neue Graphik der gemessenen Daten zeigte dann keine Abweichungen mehr von einer Geraden. Beim Vergleich der beobachteten Daten mit den gemessenen fällt die geringe Beobachtung im roten Spektralbereich auf. 3.3 Erste Aufnahme von Spektren Der Beobachtung der Spektren durch den Sucher der Spiegelreflexkamera folgte die Aufnahme mit derselbigen. Der nächste Schritt war, den Anblick durch den Sucher für die Nachwelt festzuhalten. [ 5 ] 3.3.1 Aufnahme von Spektren mit der Photokamera Der Beobachtung der Referenzpunkte folgten Probeaufnahmen dieser Punkte und des entsprechenden Sonnenspektrums mit der Photokamera. Damit sollten verschiedene Belichtungszeiten für die Referenzpunkte und das Sonnenspektrum getestet werden. Schon für die Aufnahme eines einfachen Referenzspektrums wurden Belichtungszeiten von mehr als 10 Sekunden benötigt. An die Aufnahme eines Sternspektrums war mit dieser Methode also nicht zu denken. Außerdem erschien uns die Auswertung solcher photographisch gewonnener Spektren zu umständlich und zeitintensiv, da das Spektrum eben sehr schmal auf dem Film war. Eine Auswertung mit dem Registrierphotometer wurde damit praktisch unmöglich. Wir beschlossen daher, nur noch mit CCD-Kameras, speziell mit der bei Bedarf zur Verfügung stehenden Kamera der Sternwarte, weiterzuarbeiten. 3.3.2 Beobachtung von Spektren mit einer einfachen CCD-Kamera Die Firma Kohärent stattete uns kurzzeitig einen Besuch ab, um mit dem Spektrographen die Genauigkeit eines neu entwickelten Lasers zu überprüfen. Für diesen Zeitraum stellte man uns eine einfache, recht unempfindliche CCD-Kamera mit Monitor zur Verfügung, wie sie beispielsweise für Überwachungskameras verwendet werden. Die Kamera wird anstelle der Spiegelreflexkamera in den Strahlengang des Spektrographen gehalten. Mit ihr machten wir die ersten CCD-Beobachtungen, Aufnahmen sind mit der Kamera nicht möglich. Es ist ein beeindruckendes Bild, die Natriumlinien, die 0,6 nm auseinander liegen, in der 2. Ordnung auf dem Monitor auf 16,5 cm getrennt zu sehen. Da wir aber auch Aufnahmen anfertigen wollten, und aufgrund der 40 geringen Empfindlichkeit der Kamera entschlossen wir uns jedoch, ab sofort die CCD-Kamera der Sternwarte Lübeck zu benutzen. 3.3.3 Aufnahme von Spektren mit der CCD-Kamera der Sternwarte Lübeck Die CCD-Kamera ST-6 der amerikanischen Firma SBIG ist eine hochempfindliche Kamera speziell für die Anwendung in der Astrophotographie gedacht. Sie ist heute 6 Jahre alt, zählte aber zum Kaufdatum zum Besten und mit 6000 DM Teuersten, was es damals auf dem Markt gab. Große CCD-Chips waren damals jedoch unbezahlbar. Der Chip hat eine Größe von nur 8,6 mm x 6,5 mm mit 375 x 241 Pixeln. Die Kamera wird über eine Steuerungseinheit und ein Computerprogramm wahlweise unter Windows oder DOS betrieben. Zur CCD-Kamera gehört ein ebenso alter Laptop zur Steuerung. Die Handhabung der Kamera bereitete anfangs einige Probleme, da zum einen weder ich noch Herr Kasan große Erfahrung im Umgang mit der Kamera hatten, zum anderen bedingt die hohe Empfindlichkeit, daß bereits nach kurzer Belichtungszeit das Bild durch Streulicht überbelichtet war. Frei nach Norbert Kordts: “Die Kamera registriert nachts selbst vorbeifliegende Glühwürmchen.” Wir mußten also zuerst für eine gute Isolierung des Strahlenganges im Verbindungsbereich Spektrograph-Kamera sorgen und uns in das Bedienungsprogramm der Kamera einarbeiten. Erste Versuche dem Streulicht mit Alufolie und Verdunklungsstoff entgegenzuwirken, brachten nicht das gewünschte Ergebnis. Holger Flint, ehemaliger Schüler von Herrn Kasan, AG-Mitglied und jetziger Diplomphysiker ließ uns schließlich in der Werkstatt des GKSS ein genau auf Kamera und Ansatz angepaßtes, mehrere Zentimeter dickes Aluminiumzwischenstück drehen. Das in Verbindung mit Verdunklungsstoff half dann weiter. Jetzt konnte mit den ersten Testaufnahmen am astronomischen Objekt Sonne begonnen werden. Am Freitag, den 27.03.1998 blieb ich ein wenig länger in der Schule. Ich hatte es mir mit Spektrograph, CCD-Kamera und Laptop in Herrn Kasans Büro gemütlich gemacht. Die Putzfrau betrachtete mich ein wenig mißtrauisch, wie ich auf die Tastatur des Laptops einhackte. Glücklicherweise war sie bereits ein Stockwerk weiter, als ich einen Freudenschrei ausstieß. Herr Kasan, im Nebenraum mit der Korrektur von Klassenarbeiten beschäftigt, und ich bewunderten unser erstes “Sonnenspektrum”. Die rechte Hälfte des Bildes war vollkommen überbelichtet, links zeigte sich ein heller Streifen. Ein bißchen mehr Verdunklungsstoff, kürzere Belichtungszeit, und wir hatten ein Bild mit einem schmalen wenn auch etwas schiefen Streifen auf dunklem Grund. Innerhalb des Streifens zeigten sich Helligkeitsunterschiede. Diese ersten Tests eines Sonnenspektrums waren recht einfacher Art. Da sie aufgrund ihrer großen Linienstärke eindeutig zu identifizieren sein sollten, wählte ich als Wellenlängenbereich die beiden Natriumlinien D1/D2 bei 5889,934 Åbzw. 5895,940 Å. Die Glasfaser wurde nicht auf die Sonne ausgerichtet, sondern empfing Streulicht aus dem Raum, polarisiert durch das Fensterglas. Die Belichtungszeiten lagen mit 10 bis 20 Sekunden entsprechend hoch. Ich fertigte für alle drei verfügbaren Ordnungen eine Aufnahme an, zusätzlich dazu noch drei Aufnahmen der Referenzlinien, die Glasfaser wurde dazu auf die Natriumdampflampe gerichtet. Referenzspektrum und Sonnenspektrum konnten mit dem Programm der CCD-Kamera überlagert werden. Am Ort der beiden kräftigen Emissionspunkte im Referenzspektrum zeigten sich im Sonnenspektrum klare dunkle Stellen. Weitere dunkle Punkte zwischen den eindeutig identifizierten Natriumlinien waren zu erkennen. Seit diesen Tests wurde die Kamera umgebaut. Sie verfügt jetzt über ein Adaptergewinde für Nikon-Kameraobjektive. Genau wie vorher die Spiegelreflexkamera kann die CCD-Kamera jetzt über einen Verbindungsring (T2-Ring) fest und streulichtfrei an den Spektrographen angeschlossen werden. 41 Abbildung 3.3: Das Sonnenspektrum 1. und 2. Ordnung in der Umgebung der Natriumlinien D1 /D2 bei 5889,934 Å bzw. 5895,940 Å mit überlagertem Referenzspektrum. 3.3.4 Auswertung der ersten Spektren Zur Auswertung der neuen Spektren mußte eine Methode analog zum Registrierphotometer gefunden werden, denn mit dem Photometer selbst ließen sich diese Bilder natürlich nicht auswerten. Gewünschtes Ergebnis war wie zuvor ein Graph der Intensitätsverteilung in Abhängigkeit der Wellenlänge, um das Spektrum genau zu vermessen und weitere Linien identifizieren zu können. Allerdings waren weder Herr Kasan noch ich in der Lage, ein Computerprogramm zu programmieren, daß uns diese Information direkt aus den Bilddateien der Kamera herausholt. Wenn der Computer nicht mehr weiterhilft, muß mit Bleistift und Millimeterpapier weitergearbeitet werden. In diesen Dateien werden jedem Pixel eines Bildes ein Zahlenwert als relative Intensität zugeordnet. Herr Kasan hat in mehrtägiger Arbeit die Zeilen der Bilder, auf denen die Spektren liegen, herausgesucht und zu jedem Pixel den Zahlenwert herausgeschrieben und danach erste Intensitätsverläufe auf Millimeterpapier aufgezeichnet. Das war dadurch erschwert, daß das Spektrum schief im Bild lag, so daß mehrfach die Zeilen gewechselt werden mußten. Diese Zahlenwerte in Excel eingegeben ergeben ein Diagramm, das zeigt, daß sich zwischen den beiden Natriumlinien eindeutig mehrere andere Linien befinden. Aufgrund der Linearität der Wellenlänge von der Skaleneinteilung konnte ich nach der Festlegung der Natriumlinien auf die jeweils geringsten Intensitätswerte auch die Wellenlängen für alle anderen Pixel bestimmen. Aus der Bibliothek der Sternwarte lieh ich mir ein Buch zur Identifikation der restlichen Linien aus [ 7 ]. Dort sind sämtliche bekannten Linien im Sonnenspektrum mit genauer Angabe von Wellenlänge, Äquivalentbreite und Verursacherelement angegeben. Mit Hilfe dieses Buches erwiesen sich die meisten Linien im Gesichtsfeld als Wasser aus der Erdatmosphäre. Nur wenige Linien waren anderen Elementen wie Eisen zuzuordnen. Hauptaufgabe des Spektrographen soll der Nachweis von Dopplerverschiebungen und die Berechnung der damit verbundenen Geschwindigkeiten sein. Eine Analyse des Diagramms auf dem Millimeterpapier erfüllte unsere hohen Erwartungen an das Gerät: In der Graphik sind die beiden Natriumlinien des Spektrums 2. Ordnung 13,3 cm voneinander entfernt. Kann man die Position einer Linie im Spektrum 2. Ordnung also auf 5 mm genau bestimmen, lassen sich Geschwindigkeiten bis auf 11,4 km/s genau berechnen. Läßt sich die Position der Linie auf 1 mm festlegen, erreicht die Genauigkeit sogar 2,3 km/s. 42 Natriumlinien D/D Plus2 Smooth 190 180 170 Fe I Atm HO Atm Atm HO HO Fe I 43 relative Intensität Fe II 160 Atm HO Atm HO Atm HO Atm HO Atm HO Atm HO Atm HO 150 Atm HO Atm HO Atm HO 140 130 Na I 120 5889 5890 Na I 5891 5892 5893 Wellenlänge [ Å ] 5894 5895 5896 5897 4 Die Sonne - unser nächster Stern Die Sonne ist der Stern, der der Erde am nächsten steht und damit natürlich der am besten vermessene Stern, auch spektroskopisch. Sie erscheint uns als kreisförmiges, hell leuchtendes Objekt am Taghimmel. Dabei hat sie einen scheinbaren Durchmesser von durchschnittlich 31’59”, also etwa einem halben Grad. Das genügt, um auf ihrer Oberfläche eine Fülle von Details erkennen zu können. Es gibt dunkel erscheinende Sonnenflecken mit Umbra und Penumbra und helle Fackelgebiete auf der Sonnenoberfläche. Sonnenoberfläche bedeutet Photosphäre, denn eigentlich hat die Sonne keine richtige Oberfläche. Die Photosphäre ist die Schicht der Sonne, von der das sichtbare Licht abgestrahlt wird. Sie ist nur 200 km dick, hauchdünn also im Vergleich zum Sonnenradius, der 696.000 km beträgt. Die Sonne hat eine Gesamtstrahlungsleistung von 3, 82 · 1026 W. Das erscheint ungeheuer viel, dennoch ist das für einen Stern eher durchschnittlich. Die Sonne reiht sich mit dieser Leuchtkraft unter den normalen Sternen, den sogenannten Zwergen, ein. Nach dem Stefan-Boltzmann-Strahlungsgesetz errechnet sich die Effektivtemperatur der Sonnenoberfläche zu 5770 K. Das ist jedoch nichts gegen die 15 Millionen K, die im Sonneninneren herrschen. Im Kern der Sonne wird ihre Energie erzeugt. Ca. 10 Millionen Jahre benötigt das Photon vom Kern bis an die Oberfläche und dann nur noch 8 Minuten für die 149,6 Millionen km zur Erde. 4.1 Das Sonnenspektrum Die Sonne gehört zu den G-Sternen, genauer gesagt, sie ist ein G2V- Stern. Anders als bei allen anderen Sternen bekommen wir von der Sonne so viel Licht, daß wir es in die feinsten Details auflösen können. Bereits 1802 beobachtete W. H. Wollaston die auffälligsten dunklen Absorptionslinien im Sonnenspektrum. Joseph von Fraunhofer kartierte 12 Jahre später 567 dieser Linien. Nach ihm wurden sie Fraunhoferlinien genannt. Richtig gedeutet wurden sie allerdings erst 1859, als R.W. Bunsen und G. R. Kirchhoff die Grundlagen der Spektralanalyse aus ihren Laboratoriumsversuchen ermittelten. Heute sind über 50.000 Absorptionslinien im Sonnenspektrum verzeichnet. 68 der 92 natürlich vorkommenden chemischen Elemente wurden in der Sonne spektroskopisch nachgewiesen. Das Element Helium hat seinen Namen aus der Spektralanalyse der Sonne. Man fand damals Linien im Sonnenspektrum, die keinem auf der Erde bekannten Element zugeordnet werden konnten. Das neu entdeckte Element nannte man Helium (griechisch Helios = Sonne). Neben den Elementen haben aber auch eine Anzahl Moleküle wie CH, OH, NH, O2 und CO ihre Spuren in Form von Linien und Banden im Spektrum hinterlassen. 4.1.1 Die Aufnahme des Sonnenspektrums Seit der erfolgreichen Aufnahme der Natriumlinien hatte ich mir vorgenommen, ein vollständiges, zusammenhängendes Sonnenspektrum aufzunehmen. Ich wußte, daß dies mit einem enormen Zeit- und Arbeitsaufwand verbunden sein würde und nicht innerhalb einiger Freistunden in der Schule zu machen war. Ich beschloß daher, das Spektrum bei mir zu Hause aufzunehmen. Zu diesem Zweck entlieh ich für die Woche vom 28.06. bis zum 04.07.1999 in der Sternwarte die CCD-Kamera mit Laptop und nahm aus der Schule den Spektrographen samt Zubehör mit. 44 Bei den Aufnahmen mußten alle Geräte vor direktem Sonnenlicht geschützt werden. Beim Spektrographen ging es da hauptsächlich um die Vermeidung von Streulicht im Strahlengang im Verbindungsstück Spektrograph-CCD-Kamera, und auch die Kühlung der CCD-Kamera, die zum Betrieb auf −15◦ C gekühlt werden muß, hätte direktes Sonnenlicht wahrscheinlich sehr übel genommen. Ich hatte nicht vor, wie bei den ersten Aufnahmen der Natriumlinien Streulicht zu verwenden, sondern wollte die Glasfaser direkt auf die Sonne richten. Das würde die Belichtungszeit extrem verkürzen. Aufgrund der scheinbaren Drehung der Himmelskugel hätte die Position der Glasfaser jedoch ständig verändert werden und der Erddrehung angepaßt werden müssen. Ich stellte daher meinen Refraktor ebenfalls im Garten auf. Es handelt sich dabei um einen Fraunhofer Achromaten f = 1200 mm, f/15, mit dem ich auch normalerweise die Sonne beobachte und photographiere. Das Teleskop verfügt über eine elektronische Nachführung. Die Glasfaser wurde mit Physikerallzweckgerät direkt am Fernrohrtubus befestigt. Zur Überwachung der Nachführgenauigkeit benutze ich zusätzlich den Sonnenprojektionsschirm, so daß ich das Bild der Sonne vom Laptop aus verfolgen konnte. Das Objektiv des Teleskops zusammen mit einem 25 mm Okular projiziert dazu das Sonnenbild auf einen weißen Holzschirm. Wandert das Bild der Sonne aus dem Gesichtsfeld, ist auch die Glasfaser nicht mehr genau auf die Sonne ausgerichtet und die Nachführung muß korrigiert werden. Um ein schiefes Spektrum wie bei den Natriumlinien zu vermeiden, waren Tisch und CCDKamera mit einer Wasserwaage ausgerüstet. Bei einem schiefen Spektrum wäre es außerdem sehr scher geworden, die Bilder später zusammenzusetzen. Ich hatte vor, das Sonnenspektrum in der -1. Ordnung aufzunehmen. Die Aufnahme in der zweiten Ordnung wurde dadurch verhindert, daß man ohne die noch nicht fertiggestellte Einkopplungsvorrichtung das Filter nicht verwenden konnte, so daß sich der rote Bereich der 2. Ordnung mit dem blauen Bereich der 3. Ordnung überlagern würde. Erste Testaufnahmen am 31.06. zeigten, daß ich aufgrund der geringen Größe des CCD-Chips und dem damit verbundenen kleinen Gesichtsfeld bei jedem vollen Wert der Skaleneinteilung eine Aufnahme machen m üßte, um die Bilder später überlagern zu können. Die Testaufnahmen zeigten zusätzlich ein Problem. Der Spektrumsstreifen war wesentlich breiter und damit unschärfer als noch bei den Aufnahmen der Natriumlinien. Eine Erklärung dieser Unschärfe liefert die Tatsache, daß die Kamera in der Zwischenzeit mit dem Adaptergewinde für Kameraobjektive ausgerüstet war. Durch diese Zwischenstück lag der Fokus der Kamera ganz anders. Das Aluminiumzwischenstück aus der Werkstatt des GKSS war jetzt um ca. 3 mm zu lang. Diese ungewollte Unschärfe hatte sogar einen Vorteil: Die Spektrallinien waren, da das Spektrum jetzt breiter war als zuvor, auch im Bild bereits deutlich zu erkennen. Da ich zunächst nicht wußte, wie der Fokus des Spektrographen einzustellen ist, konnte ich auch nichts gegen die Unschärfe unternehmen, dieses Problem ist inzwischen gelöst. Ich beschloß, das Spektrum von 3600 Å bis 6800 Å aufzunehmen. Das erforderte 140 Einzelaufnahmen in den Skalenteilwerten von 160 bis 300. Diese hohe Anzahl mußte auf zwei Tage zur Aufnahme aufgeteilt werden. Zwar betrugen die Belichtungszeiten je nach Empfindlichkeit der CCD-Kamera in den einzelnen Spektralbereichen nur 1/100 s bis 1/10 s, der Download der Bilder aus der Kamera auf den Rechner bedurfte ca. 3 Minuten pro Bild (386er mit 4MB RAM). So nahm ich den blauen Bereich des Spektrums am 01.07. und den roten Bereich am 03.01. 1999 auf. [ 6 ] Die Tatsache, daß durch den Eklat mit Herrn Schreiber die Kursfahrt des Physik-LKs nach München ausgefallen war (eine andere Geschichte...), verhalf mir zu zwei schulfreien Wochen kurz vor den Sommerferien. Während andere Mitglieder des Kurses bei anderen Kursfahrten mitfuhren oder bei Arbeiten in der Schule eingesetzt wurden, beantragte ich eine Befreiung zur Arbeit am Sonnenspektrum für diese Facharbeit. 45 Ein Platz an der Sonne Arbeitsplatz im Garten zur Aufnahme der Bilder für das Gesamtspektrum der Sonne am 01.07.1999 Gitterspektrograph, CCD-Kamera und Steuercomputer müssen mit einem Sonnenschirm vor der direkten Sonneneinstrahlung geschützt werden. Im Hintergrund mein Teleskop mit Sonnenprojektionsschirm. Die Glasfaser zum Spektrographen ist auf dem Fernrohrtubus befestigt. Das Teleskop wird automatisch auf die Sonne nachgeführt. Kein Platz mehr auf dem Gartentisch mit Spektrograph, Laptop, CCD-Kamera mit Steuereinheit und Kabelsalat. Abbildung 4.1: Arbeitsplatz Abbildung 4.2: Aufbau der Geräte 46 Die Sonne gefahrlos betrachtet Ein Sonnenprojektionsschirm ist die ungefährlichtste Methode die Sonne zu beobachten, hier zur Kontrolle der Nachführung. Projektion durch einen Fraunhoferachromaten mit f=1200 mm und f/15 (Vixen NP 80L). Hier Okularprojektion mi 25 mm LV-Okular, 3,84 m Äquivalentbrennweite. Die Sonne, photographiert durch ein neutrales Folienfilter der Firma Baader. Fokalaufnahme mit 1200 mm Brennweite. Aufnahme vom 30.12.1998. Gut zu erkennen: Große Fleckengruppe vom Typ F, Randverdunklung, Granulation, Fackelgebiete. Abbildung 4.3: Projektion der Sonne Abbildung 4.4: Fokalaufnahme der Sonne 47 Die Aufnahmen fanden in unserem Hintergarten statt. Es war nicht einfach, sämtliche Geräte wie Spektrograph, Laptop, CCD-Kamera mit Steuereinheit und Netzgerät auf dem Gartentisch unterzubringen. Das Arbeiten bei mir zu Hause hat den eindeutigen Vorteil, daß man selbst entscheiden konnte, wann man mit der Arbeit begann. Abhängig war ich da nur vom Wetter, ich hatte jedoch durchgängig klaren Himmel während der zweiten Hälfte der ersten Woche. Die Steuerung der Kamera per Laptop erforderte nur wenige Mausklicks, nebenbei konnte man im Liegestuhl die Sonne genießen. Was ich da so bei uns im Garten tat, mußte auf den Außenstehenden also wie Urlaub wirken, war es aber nicht. Zum Ende der Aufnahmen verpaßte das undankbare Netzgerät der Kamera mir dann auch noch mehrere elektrische Schläge, kein gutes Zeichen. Als wir die Kamera einige Monate später in Betrieb nehmen wollten, streikte sie. Gott sei Dank war nur das Verbindungskabel defekt, Einschicken zur Reparatur (in die USA) hätte wahrscheinlich Monate gedauert. 4.1.2 Digitale Weiterverarbeitung Mehrere weitere Tage erforderte dann die Weiterverarbeitung der Bilder. Die Software der CCDKamera speichert die Bilder in einem kameraeigenen Bildformat, daß von normalen Bildbearbeitungsprogrammen nicht geöffnet werden kann. Selbige Software kann dieses Format aber auch in Tif-Bilddateien umwandeln. Dafür benötigte ich einen weiteren Tag. Jetzt konnte ich die Einzelaufnahmen mit einem Bildbearbeitungsprogramm aneinandersetzen. Ich verwendete dazu mein Standart-Bildbearbeitungsprogramm Corel Photopaint. Es hat den Vorteil, daß man die einzelnen Bilder pixelweise mit den Pfeiltasten gegeneinander bewegen kann. Wenn die Bilder genau zusammenpaßten, wurden sie zusammengefügt. Das endete in einer 4 1/2 MB Photopaint-Datei und einer immer noch halb so großen Bitmap. Das Bild selbst ist genau 9,33 m lang. Ich habe ein kleines Problem damit, diese Datei vollständig auszudrucken. Ich war freudig überrascht, als ich vor zwei Jahren feststellte, daß mein neuer Drucker auch auf Endlospapier drucken kann. Sollten die vier Kartons Endlospapier, die seit ca. 10 Jahren seit der Stillegung des guten alten Nec P7 (der inzwischen wieder in Betrieb genommen wurde) bei uns im Keller lagerten, etwa noch zu etwas gut sein? Zu meinem Verdruß gibt es unter Windows nur eine Handvoll c Programme, die überhaupt Bannerdruck zulassen. Eines davon ist der Microsoft Publisher, ein Programm, daß ich auch wegen anderer Feinheiten sehr schätze. Dennoch ist auch der Publisher bei diesem Problem überfordert. Das längstmögliche Banner, daß mit Publisher auf Endlospapier gedruckt werden kann, ist 6 m lang. Und auch eine 6 m lange Graphik mag das Programm dann auch nicht mehr händeln. Da heißt es Bild verkleinern oder in drei Teilen drucken. Inzwischen existiert ein solcher Ausdruck, aber Computer und Drucker dazu zu überreden, hat mich fast einen ganzen Tag gekostet. Diese ausgerollten neuneinhalb Meter Ausdruck sind ungeheuer beeindruckend, schön ist es auch, sie hinterher wieder zusammenzurollen... 4.1.3 Auswertung des Spektrums Die Auswertung des Spektrums geht aufgrund der Linearität der Wellenlängenskala relativ einfach voran. Mit Hilfe zweier klar identifizierten Linien lassen sich allen Punkten im Spektrum Wellenlängen zuordnen. Mit Hilfe von [ 7 ] lassen sich dann sämtliche dunklen Linien identifizieren. Die große Häufigkeit von Molekülbanden hat im roten Bereich zu einem geringen Kontrast des Spektrum geführt. Ich konzentrierte mich daher auf den blauen Bereich des Spektrums. Hier findet sich der große Teil der Balmer-Serie des Wasserstoffs und die beiden auffälligen Linien des einfach ionisierten Calciums. Sonst konnte hauptsächlich Fe I identifiziert werden. Das gesamte Ergebnis ist im Anhang A2 dargestellt. Arbeitsintensiv war wiederum die graphische Darstellung von relativer Intensität in Abhängigkeit von der Wellenlänge. Ich verfügte zwar über ein kleines von Norbert Kordts geschriebenes 48 Abbildung 4.5: Das Sonnenspektrum im Bereich der Linien H und K des einfach ionisierten Calciums mit identifizierten Linien. Programm, daß die Intensität als Kurve darstellte, es ist aber weder möglich, die Graphik auszudrucken noch in eine weiterzuverarbeitende Datei umzuwandeln. Zur graphischen Darstellung mußten also noch immer die einzelnen Pixel ausgelesen werden. Für die gesamten 9,33 m des Spektrum würde das wohl den Rest meines Lebens dauern. Sollte ich also irgendwann einmal über genügend Kenntnis in Programmiersprachen verfügen dann kann die Aufgabe in Angriff genommen werden ein entsprechendes Programm zur Auswertung zu schreiben. Sobald es zur Verfügung steht, kann das Spektrum über seine 9,33 m Länge graphisch ausgewertet werden. Ich entschied mich daher die Umgebung der Linie H des einfach ionisierten Calciums nach der konventionellen Methode auszuwerten. Die Linie weist die ungeheure Äquivalentbreite von 15,5 Å auf. In unmittelbarer Nähe des Linienzentrums bei 3968,492 Å befindet sich dann auch noch die Linie He der Balmer-Serie des Wasserstoffs bei 3970,076 Å. Laut [ 3 ] ist es sehr schwierig, die Linie innerhalb der Calciumlinie des Sonnenspektrums nachzuweisen. Ähnlich wie es Herr Kasan mit den Natriumlinien tat, schrieb auch ich (teilweise mit Hilfe meine Mutter) die Intensitätswerte der einzelnen Pixel in langen Zahlenkolonnen heraus. Anders als Herr Kasan jedoch entschloß ich mich, schon aufgrund der größeren Breite der Spektren, nicht nur eine Pixelreihe auszulesen, sondern gleich mehrere. Die Werte für eine Spalte sollten dann addiert werden, um Unregelmäßigkeiten auszugleichen. Die Zahlenkolonnen für fünf Pixelreihen über je 170 Pixel füllen mehrere Seiten. Sie wurden als nächstes in ein Excel-Tabellenblatt eingegeben und die Spalten addiert. Als nächstes wurden zu den Helligkeitswerten die Wellenlängen berechnet. Dann fertigte ich ein Diagrammblatt an, in dem die Intensität in Abhängigkeit von der Wellenlänge aufgetragen ist. Innerhalb der extrem breiten Calciumlinie zeigten sich deutlich weitere Linien. Sie wurden mit Hilfe von [ 7 ] identifiziert. Im blauen Bereich des Sonnenspektrums sind wesentlich mehr kräftige 49 Linien, meist von Metallen, und nur wenige Banden zu finden, anders als im Bereich der Natriumlinien. Die meisten Linien konnten dabei wieder Fe I zugeordnet werden, aber auch Titan, Aluminium, Nickel und Chrom konnten gefunden werden. Exotisch aber auch das CH-Molek ül und das Element Europium aus der Reihe der Seltenen Erden. Klar zeigt sich Hε innerhalb der Calciumlinie. Das Profil der Linie selbst macht man sich am einfachsten durch eine unterlegte stark gemittelte Kurve klar. Nachträglich habe ich dann noch die zweite Calciumlinie K bei 3933,628 Å auf ähnliche Weise ausgewertet. Bevor hier das Diagramm entstand, wurden die Daten zunächst auf den Hintergrund korrigiert. Dazu wurden unterhalb der Zeilen mit dem Spektrum im CCD-Bild f ür drei Zeilen die Helligkeitswerte des Hintergrundes aufgenommen, gemittelt, und dann noch einmal durch Mittelung jeweils dreier benachbarter Pixel geglättet. Diese Hintergrundwerte wurden von den Zeilen des Spektrums abgezogen, bevor deren Werte aufaddiert wurden. Dadurch wird das Spektrum auf die Hintergrundhelligkeit des CCD-Bildes, die wie man im Bild erkennen kann von links nach rechts zunimmt, korrigiert. Die Auswirkungen der Korrektur zeigt ein Vergleich von korrigiertem und unkorrigiertem Linienprofil der K-Linie. Die Abweichungen sind minimal. Die Mühe der neuen Auswertung habe ich mir allerdings aus einem anderen Grund gemacht: Bei der Lektüre von [ 3 ] war mir schon zuvor ein Kapitel über Chromosphären und ihre Auswirkungen auf das Spektrum des Sterns aufgefallen. Die Chromosphäre, die Schicht der Sternatmosphäre oberhalb der Photosphäre, findet sich bei Sternen der Spektraltypen G, K und M, also auch bei der Sonne. Man weist sie durch Spektroskopie der stärksten Absorptionslinien mit besonders hoher Auflösung nach. Diese Linien sind ja eben die beiden Calciumlinien. Die Linie H ist dabei weniger geeignet, eben aus dem Grund, aus dem ich sie zuvor näher untersucht hatte, nämlich die Überlagerung mit der Wasserstofflinie. Die tiefe und breite Absorption der beiden Linien entsteht in der Photosphäre, bei der K-Linie nennt man sie K1. Die Chromosphäre dagegen besteht aus dünnem, heißerem Gas, sie erzeugt Emissionslinien. Bei hinreichend genauer Abbildung kann man die chromosphärische Emissionslinie, bezeichnet mit K2, abbilden. Im Zentrum der Emission entsteht durch Selbstabsorption in den oberen Chromosphärenschichten wiederum eine weitere Absorptionslinie, die man K3 nennt. Ich fragte mich, wie es mit der Nachweismöglichkeit der Emissionskomponente K2 im Sonnenspektrum steht. Ein Nachweis der Selbstabsorption K3 liegt jedenfalls nicht im Rahmen des Möglichen. Es war die Frage, wie stark der Emissionspeak im Vergleich zur gesamten Tiefe der Linie ist und ob dies im Rahmen der Nachweismöglichkeit des Spektrographen und der Fehlergrenzen liegt. Die notwendige Wellenlängenauflösung ist jedenfalls klar gegeben. Und tatsächlich zeigt (sowohl das korrigierte als auch das unkorrigierte) Linienprofil der K-Linie genau im Zentrum der Linie einen kleinen Peak, der sich sonst nicht erklären läßt. Ich habe mir dann bestätigen lassen, daß dessen Stärke im Vergleich zur gesamten Calciumlinie genau in dem Bereich bewegt, den die Emission haben sollte. Hierbei sollte allerdings bedacht werden, daß f ür die Datenpunkte keine exakte Fehlerrechnung durchgeführt wurde. Eine grobe Abschätzung des Fehlers für die relative Intensität durch Mittelung über die fünf Pixelzeilen des Spektrums ergibt eine Größe für den Fehlerbalken, mit der man das Feature auch wegdiskutieren könnte. Es spielt hierbei ja auch eine Rolle, daß das Spektrum ja nicht ganz scharf ist. Bei einer neuen scharfen Aufnahme würden sich allerdings durch die Reduktion auf zwei CCD-Zeilen die Fehler um einiges vergrößern. Es ist die Frage, was in diesem falle sinnvoller ist. Außerdem gilt es zu bedenken, daß die CCD-Bilder überhaupt nicht professionell korrigiert wurden. Ein einfaches Abziehen des Hintergrundes ist da nicht genug, Flatfield und Bias hätten abgezogen werden müssen. Astronomie-AG-Mitglied Thimo Langbehn war vor kurzem erfolgreicher als ich was es angeht, die Intensitätswerte für die einzelnen CCD-Pixel direkt aus der Datei auszulesen. Dazu ist anzu- 50 merken, daß ich ziemlich schnell aufgegeben habe, als ich festgestellt habe, daß die Werte nicht direkt in der Datei stehen, sondern irgendwie gepackt sind. Auf die Idee, mal im Internet nach dem Dateiformat zu schauen, hätte ich allerdings auch kommen können... Er hat draufhin ein kleines C-Programm geschrieben, daß die Werte aus der Datei in ein ASCII-File schreibt, daß man dann in Excel weiterbearbeiten kann. Das ganze läßt sich dann in 3D plotten, oder im Falle von Spektren auf 2D reduzieren. Nach einer guten Viertelstunde hatte ich mit Hilfe dieses Programms aus den CCD-Bildern der Calcium-Linien ein Diagramm erstellt, das dem handausgelesenen doch recht ähnlich sah. Man erinnere sich, mit wieviel Zeitaufwand das verbunden war. 51 Die Umgebung der Linie H des einfach ionisierten Calciums 6000 5500 Äquivalentbreite 15,467 Å von Ca II 3968,492 Å Fe I 5000 4500 Fe I 52 relative Intensität Fe I 4000 Fe I Fe I Ti I / Zr II CH Fe I 3500 3000 Fe I CH Cr I Fe I Fe I 2500 2000 Ni I Fe I / Cr I Fe I Al I 1500 Fe I Fe I Fe I Hε 1000 3957 3958 3959 3960 3961 3962 3963 3964 3965 3966 3967 3968 3969 3970 3971 3972 3973 3974 3975 3976 3977 3978 Wellenlänge [ Å ] 4300 Unkorrigiertes Linienprofil der K-Linie 3800 relative Intensität 3300 2800 2300 1800 1300 3925 3926 3927 3928 3929 3930 3931 3932 3933 3934 3935 3936 3937 3938 3939 3940 3941 Wellenlänge Korrigiertes Linienprofil der K-Linie 2950 relative Intensität 2450 1950 1450 950 450 3925 3926 3927 3928 3929 3930 3931 3932 3933 3934 Wellenlänge [ Å ] 53 3935 3936 3937 3938 3939 3940 3941 Die Linie K des einfach ionisierten Calcium bei 3933.628 Å 2950 Fe I 54 relative Intensität 2450 Mn I 1950 Fe II / Mg I / Fe I Cr I Fe I Fe I 1450 Fe I eventueller Emissionspeak K2 Fe I 950 Fe I / Co I Fe I 450 3925 3926 3927 3928 V II / Ti I / Fe I / Eu II 3929 3930 3931 3932 3933 3934 Wellenlänge [ Å ] 3935 3936 3937 3938 3939 3940 3941 5 Ausblick Die Arbeit mit dem Gitterspektrographen hat gerade erst begonnen. Natürlich haben wir uns für die Zukunft noch eine Menge vorgenommen. Da die Einkoppelvorrichtung der Glasfaser auf das Teleskop jetzt zur Verfügung steht, kann die Glasfaser nun sehr genau auf das zu spektrographierende Objekt fokussiert werden. In dieser Hinsicht ist für den Spektrographen allerdings ein Umbau geplant. Da die Luftunruhe das Bild eines Sterns im Teleskop nie vollkommen ruhig erscheinen läßt, ist eine exakte Fokussierung der extrem schmalen Glasfaser praktisch unmöglich. Sie soll durch eine breitere Faser ersetzt werden. Dadurch wird allerdings der Einbau eines Spaltes in den Spektrographen erforderlich. Die CCD-Kamera der Sternwarte ist eigentlich zur Aufnahme astronomischer Bilder und nicht als Zusatzgerät für den Spektrographen gedacht. Perfekt geeignet ist sie dafür auch nicht. Der Chip der Kamera ist recht klein und engt damit das Gesichtsfeld des aufgenommenen Spektrums ein. Eine CCD-Kamera speziell für den Spektrographen sollte einen Chip mit nur wenigen, dafür aber längeren CCD-Zeilen enthalten. Außerdem gibt es heute wesentlich empfindlichere Chips. Entsprechend ist eine weitere Diplomarbeit zur Konstruktion dieser Kamera und Programmierung der dazugehörigen Software zu vergeben. 5.1 Bestimmung von Sonnenrotation und Materiefließgeschwindigkeiten Mit Hilfe der Fokussierung der Glasfaser kann man jetzt auch kleinräumige Gebiete auf der Sonnenoberfläche näher untersuchen. Die Sonne hat eine differentielle Rotation, das heißt die Rotationsgeschwindigkeit ist abhängig von Breitengrad. Äquatornahe Schichten rotieren am schnellsten, dort beträgt die Rotationsperiode 25,03 Tage, in der Umgebung der Pole über 30 Tage. Die äquatoriale Rotationsgeschwindigkeit von ca. 2 km/s läßt sich als Dopplerverschiebung nachweisen und liegt durchaus über der Nachweisgrenze höherer Ordnungen des Spektrographen. Es werden dazu zwei Spektren vom Sonnenrand aufgenommen. Der östliche Sonnenrand bewegt sich auf die Erde zu, der westliche von der Erde weg. Die Wellenlängendifferenz der beiden Spektren läßt sich dann in die zweifache Rotationsgeschwindigkeit umrechnen. Bei gutem Seeing erkennt man die körnige Struktur der Photosphäre, die man als Granulation bezeichnet. Die Granulation unterliegt dauernder Veränderung, die Strukturen haben eine durchschnittliche Lebensdauer von ca. 10 Minuten. Die Entstehung der Granulation wird aus dem Aufbau der Sonne ersichtlich. Die Sonnenenergie wird durch Konvektion bis unter die Photosphäre transportiert. Hier steigt also Materie auf und sinkt wieder ab. Die Geschwindigkeit dieser Materiebewegung beträgt ca. 1 km/s und dürfte schon schwerer als Dopplereffekt nachzuweisen sein. Protuberanzen sind Materieauswürfe in Chromosphäre und Korona. Sie erscheinen hauptsächlich in Aktivitätsgebieten der Sonne zusammen mit Flecken, Flares und Fackeln. Man unterscheidet ruhende und aktive Protuberanzen. Sie erreichen eine durchschnittliche Höhe von 40000 km über der Sonnenoberfläche. Die Aufstiegsgeschwindigkeit aktiver Protuberanzen beträgt 100 km/s bis 1000 km/s und ist damit leicht als Dopplerverschiebungen nachzuweisen. Das Problem ergibt sich in der Beobachtung der Protuberanzen. Man benötigt Spezialgeräte wie Koronographen 55 und Protuberanzenansätze oder ein schmalbandiges Filter, zum Beispiel für die Hα-Linie des Wasserstoffs. 5.2 Bestimmung der Rotationsgeschwindigkeiten der Planeten Das Spektrum der Planeten ist ein Spiegelbild des Sonnenspektrums, da die Planeten nicht selbst leuchten, sondern nur das Sonnenlicht reflektieren. Allerdings hinterläßt die Atmosphäre des Planeten ihre “Fingerabdrücke” im Sonnenspektrum. So läßt sich die Zusammensetzung der Planetenatmosphären ermitteln. Im Vergleich zur Sonne wird die Belichtung eines Planetenspektrums natürlich länger dauern. Sie läßt sich aus der Flächenhelligkeit des Planeten und der Empfindlichkeit der CCD-Kamera für eine beliebige Ordnung berechnen. Die Rotationsgeschwindigkeit eines Planeten wird als Dopplerverschiebung analog zur Rotationsgeschwindigkeit der Sonne durch zwei Aufnahmen von den Rändern des Planeten nachgewiesen. Sie ist allerdings nur für die großen Gasplaneten meßbar. Sie beträgt für die inneren Planeten Merkur, Venus und Mars nur 3 m/s, 2 m/s und 0,24 km/s. Für die Gasriesen Jupiter und Saturn erhält man allerdings 12,7 km/s bzw. 10,2 km/s. Die Vermessung von Uranus und Neptun (4,2 km/s und 2,7 km/s) dürfte eine zu hohe Belichtungszeit erfordern. Für die Messungen dieser Dopplerverschiebungen ist der Vergleich mit einer Referenzlichtquelle nicht empfehlenswert. Es wäre erforderlich, unter anderem die Bahngeschwindigkeit der Erde und des Planeten miteinzubeziehen. 5.3 Sternspektren Der Gitterspektrograph ist zur Vermessung von Dopplerverschiebungen in Sternspektren konstruiert worden. Die Vermessung hellerer spektroskopischer Doppelsterne sollte im Bereich des Möglichen liegen. Interessant ist auch die Beobachtung im Spektrum variabler Sterne über einen längeren Zeitraum. Wir wurden zum Beispiel auf den Be-Stern γ Cassiopeiae hingewiesen. Dieser Stern ist von einer variablen heißen Gashülle umgeben, die Emissionslinien im Sternspektrum entstehen läßt. Mit der Untersuchung eines solchen Hüllensterns würde man aktuelle Forschung betreiben. Die Belichtungszeiten werden natürlich mit abnehmender Sternhelligkeit immer länger, mit mindestens 10 Minuten muß schon bei hellen Sternen gerechnet werden. Die maximale Belichtungszeit der CCD-Kamera beträgt eine Stunde. Natürlich könnten mehrere Bilder addiert werden, doch der Spektrograph erreicht hier seine natürliche Grenze. 5.4 Untersuchung des “Kordtsschen Doppelsterns” Ähnlich wie die NASA als langfristiges Ziel eine bemannte Marslandung vorgesehen hat, haben auch wir uns vor längerer Zeit die Untersuchung eines speziellen Sterns vorgenommen. Es handelt sich dabei um den 9,m 7 hellen Stern XZ13127 im Sternbild Krebs. Dieser Stern wurde am 15.04.1997 durch den Mond bedeckt. Diese Bedeckung wurde, wie viele andere zuvor, von Norbert Kordts mit dem Photometer der Sternwarte Lübeck aufgezeichnet. Die Abnahme der Helligkeit erfolgte in zwei Stufen, woraus zu folgern ist, daß es sich um einen Doppelstern handelt. Der Stern war zuvor nicht als Doppelstern bekannt, es handelt sich also um eine hauseigene Neuentdeckung. Wir haben uns vorgenommen, den Stern zu untersuchen, vielleicht erweist er sich als spektroskopischer Doppelstern. Die geringe Helligkeit des Sterns dürfte dieses Vorhaben allerdings sehr erschweren. 56 6 Literatur- und Quellenverzeichnis [1] Bergmann/Schaefer; Lehrbuch der Experimentalphysik Band 3: Optik, 9.Auflage 1993, de Gruyter Verlag [2] Friedrich Gondolatsch, Gottfried Groschopf, Otto Zimmermann; Astronomie I & II, Klett [3] James B. Kaler; Sterne und ihre Spektren, Spektrum akademischer Verlag [4] Carolin Liefke; Der Spektrograph, Polaris Ausgabe Nr. 42 [5] Carolin Liefke; Der Spektrograph Part II, Polaris Ausgabe Nr. 43 [6] Carolin Liefke; 9,33 Meter Sonnenspektrum, Polaris Ausgabe Nr. 49 [7] Charlotte E. Moore, M. G: J. Minnaert, J. Houtcast; The Solar Spectrum 2935 Åto 8770 Å, National Bureau of Standards [8] Bernd van der Smissen; Diplomarbeit. Entwurf und Konstruktion eines Spektrographen für die Messung der Dopplerverschiebungen von Sternen [9] Alfred Weigert, Heinrich Wendtker; Astronomie und Astrophysik. Ein Grundkurs. VCH Verlagsgesellschaft 57 Zum Aufbau des Spektrographen 1. Anschluß der Glasfaser Glasfaser mit 25 mm Innendurchmesser 2. Hohlspiegel (Kollimator) Brennweite 660 mm Durchmesser 100 mm 3. Reflexionsgitter 1302 Furchen pro mm Breite 60 mm Blazewinkel Θ18◦ 4. Drehpunkt des Gitters 5. erster abbildender Spiegel Bestandteil des Kutterschen Schiefspieglers 6. zweiter abbildender Spiegel Bestandteil des Kutterschen Schiefspieglers 7. Anschluß von Spiegelreflex- oder CCD-Kamera Bildebene 8. Trockenmitteleinschub schützt das Gitter vor Luftfeuchtigkeit 9. Gitterantrieb zur Drehung des Gitters 10. Fokussiertrieb 58 59





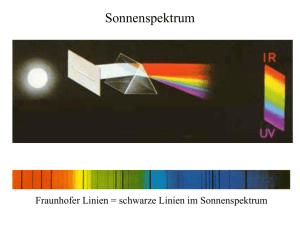

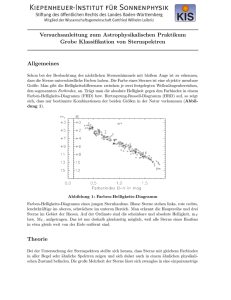
![Ein Tierversuch gilt als abgeschlossen, wenn […] soweit genetisch](http://s1.studylibde.com/store/data/001804795_1-f1d1533651f8f89ddfe57c3e71629de9-300x300.png)