Geometrie Modul 4b
Werbung

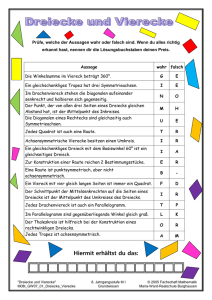
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft – DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere • • 28.10. V1 04.11. V2 Geometrische Grundbegriffe Grundkonstruktionen und Bestimmungslinien • 11.11. V3 • 18.11. V4 • • • 25.11. V5 02.12. V6 09.12. V7 Dreiecke und ihre Eigenschaften (Winkel, Kongruenzsätze, Linien/Punkte, Typisierung, Symmetrien, Winkelsätze) Vierecke und ihre Eigenschaften (Typisierung, besondere Vierecke, Haus der Vierecke, Symmetrien) Dreiecke (Flächensätze, Ähnlichkeit) Vielecke (Sätze, Winkel, Symmetrien, Beziehungen zum Kreis) Kreis (Geraden, Punkte, Typisierung, Symmetrien, Winkelsätze) • • 16.12. V8 13.01. V9 Kongruenzabbildungen - Symmetrie Flächeninhalt und Umfang von Vielecken und Kreisen • 20.01. V10 Typisierung von Körpern (Quader, Prismen, Spitzkörper, Platonische Körper, Kugel) • 27.01. V11 Rauminhalt von Körpern (Rauminhalt von Prismen und Spitzkörpern, Rauminhalt und Oberfläche der Kugel) • 03.02. V12 Zusammenfassung • 12.02. (Freitag) 14-16 Uhr, Klausur (HS 1, HS 2) 1 V4 Vierecke und ihre Eigenschaften • 1 Begriffe und Bezeichnungen • 2 Vierecke und ihre Eigenschaften • 3 Achsensymmetrische Vierecke Quellen: Kusch/Glocke. Geometrie und Trigonometrie 2008. Krauter. Erlebnis Elementargeometrie 2007. Stein. Einführung in die Mathematik II. 1997 2 1 Begriffe und Bezeichnungen • Verbindet man vier Punkte A, B, C, D einer Ebene, von denen keine drei auf einer Geraden liegen, „der Reihe nach“ miteinander, können unterschiedliche Figuren entstehen: – ein konvexes Viereck – alle Diagonalen verlaufen im Innern der Figur (1. Figur) – ein nicht-konvexes (konkaves) Viereck – eine Diagonale verläuft außerhalb der Figur (2. Figur) – ein überschlagenes Viereck – zwei der vier Strecken haben einen gemeinsamen Punkt, der nicht Endpunkt der Strecken ist (3.Figur) 3 • Wenn vier Punkte A, B, C, D, von denen nicht 3 auf einer Geraden liegen, so in einer Ebene liegen, dass die Strecken AB, BC, CD, DA außer ihren Endpunkten keine weiteren gemeinsamen Punkte haben und die Diagonalen mit Ausnahme ihrer Endpunkte ganz im Innern der Figur liegen, so bilden die Punkte A, B, C, D und die dazugehörigen Strecken ein konvexes Viereck. 4 2 Vierecke und ihre Eigenschaften Trapez, Parallelogramm, Raute, Rechteck, Quadrat, Drachenviereck 5 (1) Das Trapez und seine Eigenschaften • Wenn in einem Viereck ein Paar Gegenseiten parallel ist, nennt man es ein Trapez. • Hat ein Trapez Gegenseiten, die nicht parallel zueinander sind, so nennt man diese Schenkel. Sind die Schenkel gleichlang, spricht man von einem gleichschenkligen Trapez. • Die Höhe markiert den Abstand der parallelen Geraden voneinander. 6 Winkel im Trapez • Entgegengesetzte Winkel an geschnittenen Parallelen ergänzen sich zu 180°. • Die einem Schenkel eines Trapezes anliegenden Innenwinkel (entgegengesetzte Winkel) ergänzen sich zu 180°. -Stufenwinkel an geschnittenen Parallelen -Wechselwinkel an geschnittenen Parallelen -Wiederholung: entgegengesetzte Winkel an geschnittenen Parallelen (liegen auf der gleichen Seite der schneidenden Gerade aber auf verschiedenen Seiten der Parallelen) Versuchen Sie diese Aussage zu begründen. 7 Die Mittellinie eines Trapezes (s. auch Bestimmungslinie „Mittelparallele“) c d b m a • Die Länge m der Mittelline eines Trapezes berechnet sich aus den Längen der Seiten a und c zu: m = ac 2 8 (2) Das Parallelogramm und seine Eigenschaften • Wenn in einem Viereck beide Gegenseiten-Paare parallel sind, nennt man es Parallelogramm. • Die auf den Lotgeraden von einer Seite auf die dazu parallele Seite liegenden Strecken zwischen den Seiten sind die Höhen. 9 • Benachbarte Winkel ergänzen einander an jeder Seite zu 180°. • Das Ziel ist, zu begründen: Gegenüberliegende Winkel sind gleich groß. 10 Gegenseiten im Parallelogramm • Gegenseiten im Parallelogramm sind gleich lang. • Diesen Satz kann man mit Hilfe der Kongruenz geeigneter Teildreiecke belegen. 11 • Voraussetzung: AB und DC sowie AD und BC sind Seiten eines Parallelogramms ABCD; AC ist Diagonale im Viereck ABCD • Behauptung: Gegenseiten im Parallelogramm sind gleichlang. • Beweis: – Idee: ∆ ABC und ∆ ADC sind kongruent. – Seite AC gemeinsam; anliegende Winkel Wechselwinkel an geschnittenen Parallelen, also <BAC =<ACD und <CAD = <BCA, – daraus folgt ∆ ABC ∆ ADC nach WSW. – Gleichliegende Stücke in kongruenten Dreiecken sind gleichlang, also AB = DC und AD = BC. 12 Anwendungen in der Mechanik • Auch die Umkehrung des Satzes gilt: • Sind in einem Viereck die Gegenseiten gleich lang, so sind sie auch parallel. • Diese Eigenschaft macht man sich in der Praxis bei sogenannten Gelenkparallelogrammen zu Nutze. Ihre Innenwinkel kann man kontinuierlich verändern, trotzdem bleiben die Gegenseiten parallel, weil sie gleichlang sind. 13 Diagonalen im Parallelogramm • Vermutung: Die Diagonalen halbieren einander. • Beweisidee: Nachweis über kongruente Dreiecke • Man könnte z. B. die beiden eingefärbten Dreiecke auf Kongruenz untersuchen. • Für diese Dreiecke gilt: – a = c nach Voraussetzung – < ECD = < EAB als Wechselwinkel an geschnittenen Parallelen – < CDE = < ABE als Wechselwinkel an geschnittenen Parallelen – … 14 (3) Die Raute (Rhombus) und ihre Eigenschaften • Die Raute ist ein spezielles Parallelogramm. Nicht nur ihre Gegenseiten, sondern alle vier Seiten sind gleich lang. • Die Diagonalen einer Raute – halbieren einander, – stehen senkrecht aufeinander und – halbieren die Innenwinkel. 15 (4) Das Rechteck und seine Eigenschaften • Auch das Rechteck ist ein spezielles Parallelogramm. Seine Gegenseiten sind parallel und gleich lang, aber nicht nur einander gegenüberliegende Winkel sind gleich groß, sondern alle seine Innenwinkel sind gleich groß, d. h. jeder von ihnen muss 90° sein. • Wie in jedem Parallelogramm halbieren die Diagonalen einander. 16 Diagonalen im Rechteck sind gleich lang. • Vermutung: Diagonalen im Rechteck sind gleich lang. Auch dies kann man über geeignet gewählte kongruente Dreiecke beweisen. • Man betrachtet im Rechteck ABCD die Dreiecke ABC und CDB. – Von ihnen ausgehend weiß man: AB = CD; BC = BC; < ABC = < BCD nach Voraussetzung – Es gilt also: Dreieck ABC Dreieck BCD nach SWS. – Die Seiten AC und BD sind gleichliegende Stücke in diesen kongruenten Dreiecken und deshalb gleich lang, was zu beweisen war. 17 • In der Praxis werden Diagonalen von Rechtecken oft zur Versteifung von Holzund Eisenkonstruktionen verwendet. 18 Zusammenfassend: Beweise zu Eigenschaften von Vierecken erfolgen häufig auf der Grundlage kongruenter Teildreiecke, s. vorige Folien: Gegenseiten im Parallelogramm sind gleichlang: nach WSW Diagonalen im Parallelogramm halbieren einander: nach WSW Diagonalen im Rechteck sind gleichlang: nach SWS 19 (5) Das Quadrat und seine Eigenschaften • Das Quadrat ist eine spezielle Raute – es hat nicht nur vier gleich lange Seiten, sondern auch vier gleich große Innenwinkel von je 90°. • Das Quadrat ist auch ein spezielles Rechteck – es hat nicht nur vier gleich große Innenwinkel, sondern auch gleich lange Seiten. • Die Diagonalen des Quadrats – – – – halbieren einander, stehen senkrecht aufeinander, halbieren die Innenwinkel, sind gleich lang. 20 Bei der Betrachtung von Vierecken kann man von Paaren paralleler Seiten ausgehen. • Ein Trapez hat 1 Paar paralleler Gegenseiten. • Ein Parallelogramm hat 2 Paar paralleler Gegenseiten. • Eine Raute hat 2 Paar paralleler Gegenseiten und alle Seiten sind gleich lang. • Ein Rechteck hat zwei Paar paralleler Gegenseiten, und alle Innenwinkel sind gleich groß. • Ein Quadrat hat 2 Paar paralleler Gegenseiten und alle Seiten sind gleich lang und alle Winkel sind gleich groß. Ein Quadrat ist also eine spezielle Raute, ein spezielles Rechteck, damit auch ein spezielles Parallelogramm. Nur ein spezielles Viereck, lässt sich in diese Übersicht nicht einpassen: das Drachenviereck. 21 (6) Das Drachenviereck und seine Eigenschaften • Man kann Vierecke auch bezüglich der Länge der Nachbarseiten unterscheiden. • Das Drachenviereck hat genau zwei Paar benachbarter gleich langer Seiten. • Im Drachenviereck stehen die Diagonalen senkrecht aufeinander. • Die Diagonalen zerlegen das Drachenviereck in zwei gleichschenklige und zwei kongruente Teildreiecke. • Diejenige Diagonale, die Basis der gleichschenkligen Teildreiecke ist, wird von der anderen Diagonalen halbiert. 22 3 Symmetrische Vierecke • Figuren, für die es (mindestens) eine Gerade gibt so, dass Teilfiguren aufeinander fallen, wenn man die Figur entlang dieser Geraden faltet, heißen achsensymmetrische Figuren. Die betreffende Gerade heißt Symmetrieachse. • Solche Figuren werden auch als spiegelgleich (bezüglich einer Geraden) bezeichnet. Denn, wenn man auf ihre Symmetrieachse einen Spiegel stellt, fällt das Spiegelbild der einen Teilfigur mit der anderen Teilfigur zusammen. Für Symmetrieachse wird auch der Begriff „Spiegelachse“ verwendet. 23 • Die Verwandtschaften zwischen den verschiedenen Vierecksarten lassen sich im Haus der Vierecke veranschaulichen. 24 Studienaufgabe zur Vorbereitung auf die Übung (Woche vom 23.11. – 27.11. 2015) • Skizzieren Sie „das Haus der Vierecke“ und interpretieren Sie die dort repräsentierte Begriffshierarchie anhand unterschiedlicher Eigenschaftsgruppen (Seitenlängen, Parallelität, Diagonalen, Winkel, Symmetrie). 25