Statistische Methoden für Bauingenieure WS 13/14

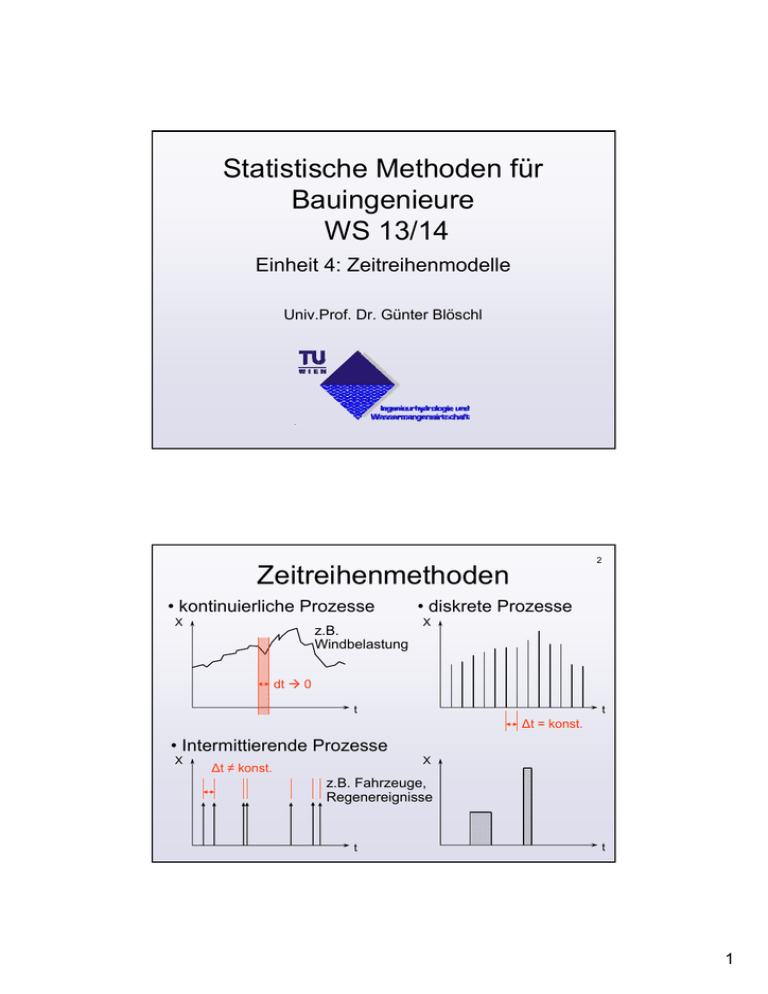
Statistische Methoden für
Bauingenieure
WS 13/14
Einheit 4: Zeitreihenmodelle
Univ.Prof. Dr. Günter Blöschl
2
Zeitreihenmethoden
• kontinuierliche Prozesse
X
z.B.
Windbelastung
• diskrete Prozesse
X
dt  0
t
t
∆t = konst.
• Intermittierende Prozesse
X
X
∆t ≠ konst.
z.B. Fahrzeuge,
Regenereignisse
t
t
1
3
Kontinuierliche Prozesse
Annahme: aufeinanderfolgende Werte sind korreliert
Kovarianz für Zeitverschiebung :
σ XY ( τ)  E ( X t  X )  ( X t τ  X )
r
• Autokorrelationsfunktion =
Korrelationskoeffizient von
Wertepaaren mit Abstand τ
ρ( τ ) 
mit sich selbst „perfekt“ korreliert
 abnehmend mit
zunehmender
Zeitverschiebung
1
σ XY ( τ)
σ x2
τ
0
4
Diskrete Prozesse
Annahme: aufeinanderfolgende Werte sind korreliert
Kovarianz für Verschiebung k Zeitschritte:
SXY (k ) 
1 n k
 ( x(i )  X )  ( x(i  k )  X )
n  k i 1
k=0,1,2,3,..
r
• Autokorrelationsfunktion =
Korrelationskoeffizient von
Wertepaaren mit Abstand k
r(k) 
1
 abnehmend mit
zunehmender
Zeitverschiebung
s XY (k)
s x2
0
1
2
3
4
5
k
2
5
• Autokorrelationsfunktion
Beispiel: Wasserwirtschaftlicher Speicher
mittlere Aufenthaltszeit TA
r
TA= 0,07 Jahre
(Jahresspeicher)
TA= 1,49 Jahre
(Überjahresspeicher)
r
1
1
0,5
0,5
0
Zufluss
Abgabe
0
10
20
30 k
-0,5
10
20
30 k
-0,5
k ... Zeitversatz (Monate)
Zeitreihenmodelle
• Zur Vorhersage
(z.B. Hochwasservorhersage)
3
2
x
1
0
-1
-2
0
10
20
10
20
t
30
40
50
30
40
50
3
2
1
x
• Zur Generierung von
Zeitreihen (Simulationen)
für die Planung von
Ingenieurmaßnahmen
(z.B. Belastungen)
6
0
-1
-2
0
t
Vergangenheit Zukunft
(Messung) (Vorhersage)
3
7
Zeitreihenmodelle
Vorgangsweise:
• Datenerhebung
• Modellwahl
• Parameterschätzung durch Analyse der Daten
• Simulation / Vorhersage
8
Modelltypen (statistische Prozesse)
1. AR(p) - Autoregressives Modell
AR(1) - Autoregressives Modell (Sonderfall)
2. MA(q) - Moving Average Modell
3. ARMA(p,q) - Autoregressives Moving Average
Modell
4. ARIMA(p,d,q) - Autoregressives Integrated
Moving Average Modell
4
9
1. AR(p)- (Autoregressive) Modelle
X t  β0  β1  X t 1  β2  X t 2  ...  β p  X t  p  Zt
AR(1) Prozess (Markov Prozess)
... als Vereinfachung eines AR Prozesses
X t  β1  X t 1  Zt
... Zufallsvariable
... vorhergehender simulierter Wert
r1 ... Autokorrelationskoeffizient
für k=1
Autoregressive Prozesse beschreiben die Eigendynamik der
Zeitreihe.
10
Bezug eines AR(1) Prozesses zur Autokorrelationsfunktion
X t  β1  X t 1  Zt
r
r (k )  r (1)k  eln(r (1))k  e β k
1
r (1)  r1
β0
r1
0
1
2
3
k
Ein AR(1) Prozess besitzt eine
Autokorrelationsfunktion, die exponentiell abnimmt.
5
Wahl der Varianz der Zufallsvariablen
σ Z2  E r1  X t 1  Zt  2 


11
 
 E r12  X t 12  2 E r1  X t 1  Zt   E Zt 2 
2
2
σX
 r12  σ X
 σ Z2 
2
σ Z2  σ X
 (1  r12 )
Varianz
des
Fehlers
Xt 
... bei glatten Prozessen „klein“
Autokorrelationskoeff.
Varianz
für (τ = 1)
der
simulierten
Größe
r1  X t 1  Zt0
1
2 2
 σ X  (1  r1 )
N(0,1) Normalverteilung Mittelwert 0, Varianz 1
12
Bezug eines AR(1) zu Übergangswahrscheinlichkeiten
Verteilungsfunktion
bedingte Wahrscheinlichkeit
F( X j X j-1, X j- 2, ... X1) 
F( X j X j-1, X j- 2, ... X j-k )
F( X j X j-1, X j- 2, ... X1) 
F( X j X j-1)
... für AR (1)
i
j
1
2
3
4
1
2
3
1
0,3 1
0,1 0,3 1
0,1 0,3
4
1
Wahrscheinlichkeit, dass Ereignis A zum
Zeitpunkt j auftritt, wenn es zum Zeitpunkt i
aufgetreten ist  bedingte Wahrscheinlichkeit
6
13
Matlab Code
n=10000;
% Korrelationskoeffizient für die zu generierende Reihe
r=0.3
s1=1;
% Standardabweichung d. unabhängigen Variablen
se=s1*sqrt(1-r*r) % Standardabweichung der Residuen
eps = normrnd(0,se,n,1);
% Normalverteilte Zufallszahl
x(1)=0
t(1)=1
for i=2:n
x(i)=x(i-1)*r+eps(i);
% AR(1) Markov-Prozess
t(i)=i;
end
plot(t,x),
% Compute the ACF (Autokorrelationsfunktion)
[ACF, Lags, Bounds] = autocorr(x, [30], 2);
plot (Lags,ACF, 'r', 'LineWidth',2,'Markersize',24)
• Zeitreihe
wenig korreliert
14
stark korreliert
• Autokorrelationsfunktion
7
15
2. MA(q)- (Moving Average) Modell
X t  α1  Zt 1  α 2  Zt 2  ...  α q  Zt q
αi
Gewichtsfunktion αi
α2 α1
αq
t
Zufallsprozess Zt
Zt
t-1
∆t
Xt
t
t
X
t
16
MA(q)- Prozess
1
α
... selten in der Hydrologie, häufiger in
Kombination mit AR-Modellen
0
t
Beispiel MA(9)- Prozess (9 Gewichte)
q=9
αi ... Gewichtsfunktion
Zt ... Zufallsprozess
Xt ... Gleitmittelprozess q-ter Ordnung
X t  α1  Zt 1  α 2  Zt 2  ...  α q  Zt q
8
Mittelbildung erzeugt
Autokorrelation
17
Autokorrelationsfunktion:
q-k
MA(q)- Prozess
r(k) 
rk  0
 α j  α j k
j 0
q-k
2
α j
j 0
für k  1, ... , q
für k  0 und k  q
18
3. ARMA(p,q)- (Autoregressive- Moving
Average) Modelle  Simulation stationärer
Prozesse
X t  β1  X t 1  β2  X t 2  ...  β p  X t  p 
 Zt  α1  Zt 1  α 2  Zt 2  ...  α q  Zt q
ARMA(p,0) = AR(p)
ARMA(0,q) = MA(q)
ARMA (p,q) = ARIMA (p,0,q)
Vorteil von gemischten Modellen:
• geringere Anzahl von Parametern und
leichtere Schätzung der Modellkoeffizienten
9
19
ARMA (1,1)
X t  β  X t 1  Zt  α  Zt 1
autoregression - moving average
r1 
- ( α )  (1 - αβ )
1  2 αβ  α 2
r1, r2 aus Daten
r2  β  r1
Gleichung nach α, β lösen
4. ARIMA(p,d,q)- (Autoregressive Integrated
Moving Average) Modell
20
w t  β1  w t 1  β2  w t 2  ...  β p  w t  p 
 Zt  α1  Zt 1  α 2  Zt 2  ...  α q  Zt q
ARIMA (p,d,q)
X t  w t  ∆d X t
Differenzenordnung
d 1
w t  ∆X t  X t  X t 1
d 2
w t  ∆X t  ∆X t 1  ( X t  X t 1 )  ( X t 1  X t 2 ) 
 X t  2 X t 1  X t 2
... Differenzenbildung zur Eliminierung von Trends
 Simulation nicht stationärer Prozesse durch stationäre
Modelle  ersetzen der ZR- Werte durch ihre Differenzen
10
21
Parameterschätzung für
Zeitreihenmodelle
... aus der Autokorrelationsfunktion geschätzt.
Für AR(1):
entweder
r
r
1
oder
1
r1
0
1
r1
für AR(1)
2
k
3
0
1
Anpassen
von e-β
2
k
3
22
Wichtig: Simulation in Hinblick auf statistische
Eigenschaften testen, ob jene der Vorgabe
entsprechen
a) Verteilungsfunktion
b) Autokorrelationsfunktion
F(x)
r
Simulation
1
Daten
Daten
Simulation
x
k
Simulation
falsch
τ
11
23
intermittierende Prozesse
• Poisson Impuls Modell
(Grundgesamtheit)
X
f
Ereignis
f ( τ1 )  a  e aτ
τ1
t
1
τ1
t
 zeitliche Abstände (τ) zwischen den Ereignissen sind
voneinander unabhängig und
 folgen einer Exponentialverteilung
 Das „Gedächtnis“ eines Poisson Prozesses kommt durch
Addition der zeitlichen Abstände  Zeitpunkte des Auftretens
sind nicht unabhängig!
24
Wahrscheinlichkeit für das Auftreten von k
Ereignissen im Intervall t ist binomialverteilt
 ∞ ... Poissonverteilung
(a  t )k at
p(k ,t ) 
e
k!
a t  μ
Schritte zur Generierung eines Poisson Prozesses
1. Analyse der Zeiten zwischen den Ereignissen (Niederschlag)
Σhr
hr
Verteilungsfunktion F
Dichtefunktion f
τ1
τ1
12
25
2. Schätzung des Poisson Parameters a
3. Ziehen von gleich verteilten Zufallszahlen U(0,1)
4. Transformation auf Exponentialverteilung mit
Parameter a, τi
5. Abfolge von Ereignissen berechnen
dt
t
X(t)
8
tk
6
4
X(tk)=k
ti
t2
t i  t i 1  τ i
2 t1
0
X(t)
τ2
τ1
t
τi
t
• Markov – Rechteck – Impuls Prozess
X
26
Ereignis
τi
Poisson Prozess
Abstand τi
t
X
Intensität in
Dauer τn
t
X
Überlagern der
Ereignisse
t
X (t )   X (i )
n
n ... Anzahl der Ereignisse für ein Gesamtereignis
13
27
Beispiel: Simulation von Niederschlagszeitreihen
Niederschlag in mm/h
25.0
20.0
15.0
10.0
5.0
0.0
0
50
100
150
200
Zeit in h
14