Physikalisches Praktikum II

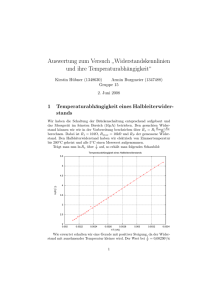
Physikalisches Praktikum II
Versuch P2-51/52
Widerstandskennlinien
Tim IJsselstein
Thomas Wielatt
Versuchsauswertung
Aufgabe 1. Temperaturabhängigkeit eines Halbleiterwiderstandes
Entsprechend der Aufgabenstellung wurde von uns der Halbleiterwiderstand über eine Wheatstonsche
Brückenschaltung ermittelt. Dabei wurde die Schaltung so aufgebaut, dass das Verhältnis zweier
Potentiometerhälften ( Gesamtpotentiometer-Widerstand : R1,2 = 1 kΩ ) gleich dem Verhältnis eines bekannten
Widerstandes von 101 Ω und dem Halbleiterwiderstand ist. Somit ergibt sich der gesuchte widerstand bei den
jeweiligen Temperaturen zu :
Rx =
RP1
* R3
RP 2
Im Laufe des Versuches wurde nun die Temperatur des Halbleiters von der Zimmertemperatur ausgehend auf
200°C erhöht. Im Verlauf dieser Temperaturänderung wurde die Wheatstonsche Brücke immer wieder so
eingestellt, dass mit dem Amperemeter zwischen den beiden Referenzpunkten kein Strom zu messen war, was
sie Vorraussetzung für die obige Beziehung ist. Die sich so Ergebenden Messpunkte sind in folgender Tabelle
dargestellt:
Temperatur [ °C ]
43
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
Anzeige auf Potentiometer
R1 [ Ω ]
5700
5110
4365
3720
3170
2690
2310
1980
1660
1430
1250
1090
960
880
760
680
670
Gegenstück Poti
R2 [ Ω ]
4300
4890
5635
6280
6830
7310
7690
8020
8340
8570
8750
8910
9040
9120
9240
9320
9330
R3 Diodenwiderstand
[Ω]
RD(T) [ Ω ]
101
133,884
101
105,544
101
78,237
101
59,828
101
46,877
101
37,167
101
30,339
101
24,935
101
20,103
101
16,853
101
14,429
101
12,356
101
10,726
101
9,746
101
8,307
101
7,369
101
7,253
Aus der Vorbereitung wissen wir, dass die Abhängigkeit des Widerstandes von der Temperatur durch folgende
Beziehung gegeben ist:
b
R(T ) = a * e T
Mittels logarithmieren kann diese Beziehung auf eine leicht auszuwertende, linearisierte Form gebracht werden.
Über die Steigung und den y-Achsen-Abschnitt der sich aus den Messpunkten ergebenden Regressionsgeraden
lassen sich die gesuchten Konstanten in der Formel bestimmen.
ln( R(T )) = ln(a) +
1/T
3,16E-03
3,09E-03
3,00E-03
2,91E-03
2,83E-03
2,75E-03
2,68E-03
2,61E-03
2,54E-03
2,48E-03
2,42E-03
2,36E-03
2,31E-03
2,26E-03
2,21E-03
2,16E-03
2,11E-03
Halbleiterwiderstand
5,000
y = 2822,7x - 4,1216
4,500
ln ( RD ) [ K ]
ln ( RD(T) )
[K]
4,897
4,659
4,360
4,091
3,848
3,615
3,412
3,216
3,001
2,825
2,669
2,514
2,373
2,277
2,117
1,997
1,981
b
T
4,000
3,500
3,000
2,500
2,000
1,500
2,000E-03
2,200E-03
2,400E-03
2,600E-03
2,800E-03
3,000E-03
3,200E-03
1/T [1/ K ]
Somit ergibt sich für die Konstanten und letztlich für die gesuchte Formel:
2822,7 = b
-4,1216 = ln(a) → 0,016 = a
R(T ) = 0,016 * e
2822, 7
T
Nun sollte aus diesem Verhalten des Halbleiters noch seine verschiedenen Anwendungsmöglichkeiten
angerissen werden. In allen Fällen beruht diese auf dem eben verifizierten Gesetz, nach dem die Temperatur und
der Widerstand des Halbleiters zueinander in Beziehung stehen.
a) Temperaturmessung : Kennt man die genauen Konstanten in der Temperaturabhängigkeit eines gewissen
Halbleiters, so kann man aus dem ermittelten Widerstand ( konstante Spannung,
Strom messen ) auf die Temperatur rückschließen.
b) Füllstandsanzeige :
Der Halbleiter wird über die gesamte Länge eines Flüssigkeitsbehälters angebracht. Je
mehr der Halbleiter in der Flüssigkeit ist, desto mehr wird er die Temperatur der
Flüssigkeit annehmen. Dadurch verändern sich der Widerstand des Halbleiters und
somit auch der Strom bei einer konstanten, angelegten Spannung. Über die Stärke des
Stromes kann somit auf die Füllstandshöhe rückgeschlossen werden.
c) Strombegrenzung :
Schaltet man einen NTC-Widerstand parallel zu einem Bauteil, so wird er bei erhöhter
Stromzufuhr erwärmt, wodurch sein Widerstand sinkt. Dies hätte zur Folge, das mehr
Strom über den Widerstand geführt wird, was dann das zu schützende Bauteil
entlastet.
Aufgabe 2. Verschiedene arten von Widerständen
2.1. Kennlinie eines Edelmetallwiderstandes
Im Folgenden wurde nun, über eine Halbwellenschaltung, die Spannungsabhängigkeit eines Edelmetallwiderstandes auf einem Oszi-Bildschirm dargestellt. Entsprechend der Erwartung ergab sich ein linearer
Zusammenhang zwischen Strom und Spannung ( Bild 1 des Bildprotokolls ). Am Oszillographen lassen sich
natürlich nur Spannungsänderungen darstellen. Deshalb wurde ein konstanter Widerstand von 101 Ω
vorgeschaltet, der nach dem ohmschen Gesetz eine direkte Proportionalität zwischen Strom und Spannung
herstellt. Es lässt sich somit die Y-Achse des Oszi-Schirmes leicht in die gesuchten Stromwerte umrechnen.
Berücksichtigt man die Skalen der Darstellung, ist nach dem ohmschen Gesetz die Geradensteigung dem
gesuchten Edelmetallwiderstand gleichzusetzen.
X-Achse : Skala → 1 V pro Skalenteil
Y-Achse : Skala → 1 V pro Skalenteil ; daraus ergibt sich mit vorgeschaltetem 101 Ω Widerstand
→ 9,9 mA pro Skalenteil
Die Geradensteigung ergibt sich nun zu:
1V * 4,5
= 113,6Ω
9,9mA * 4
Des Weiteren haben wir qualitativ die Einwirkung von Wärme auf das Edelmetall untersucht. Hierzu erwärmten
wir es mittels eines Föns und beobachteten de Reaktion auf dem Oszi-Bildschirm.
Wie im Bildprotokoll gestrichelt wiedergegeben sank der Widerstand des Edelmetalls, was sich in einem
abflachen der angezeigten Geraden widerspiegelte.
2.2. Kennlinie eines Kaltwiderstandes.
In diesem Aufgabenteil sollte nun der Kaltwiderstand einer handelsüblichen 60 Watt Glühbirne ( Wolframdraht )
mit dem, aus den Kenndaten ermittelten, Betriebswiderstand der Glühbirne verglichen werden. Während der
Betriebswiderstand bereits in der Vorbereitung zu 882 Ω berechnet wurde, bestimmten wir den Kaltwiderstand
über ein Ohmmeter. Diese Messung ergab :
64,75 Ω
Hieraus ist deutlich zu erkennen, dass bei der Glühlampe mit Wolframdraht ein Kaltleiter verwendet wurde.
D.h.: Je höher die Temperatur, desto höher der Widerstand.
Der sich durch den geringen Anfangswiderstand ergebende, hohe Anfangsstrom führt deshalb zu keinerlei
Schäden, da er schnell zu einer Erwärmung führt, was den Widerstand des Drahtes steigen lässt, wodurch die
Stromstärke abnimmt.
2.3. Kennlinie einer Kohlefadenlampe
Diese Aufgabe wurde analog zur vorangehenden Aufgabe durchgeführt, mit dem einzigen Unterschied, dass
dieses mal eine 50 W Kohlefaserlampe verwendet wurde. Der Betriebswiderstand berechnete sich in der
Vorbereitung zu 1058 Ω. Der Kaltwiderstand wurde im Versuch von uns mit folgendem Wert bestimmt :
1688 Ω
Dieser Wert zeigt uns deutlich, dass in diesem Fall ein Heißleiter vorliegt. D.h.: je höher die Temperatur, desto
geringer der Widerstand.
Die unterschiedliche Helligkeit der beiden Lampen begründet sich darin, dass man die Wolframdrahtlampe
näher an den Schmelzpunkt bringen kann, als die Kohlefaserlampe. Bei dieser besteht die Problematik, dass die
Kohle dazu neigt direkt zu sublimieren. Dies führt dazu, dass der Draht an Substanz verliert und schnell
durchbrennt. Um diesen Effekt des Durchbrennens hinauszuzögern kann das Material nicht so nahe an den
Schmelzpunkt gebracht werden, was Helligkeitseinbusen mit sich bringt.
Aufgabe 3. I/U-Abhängigkeit verschiedener Dioden
In dieser Aufgabe wurden nun unterschiedliche Dioden und ihre Kennlinien verglichen. Dabei wurden alle
Diodenkennlinien über die bereits bekannte Halbwellenschaltung aus Aufgabe 2.1. sichtbar gemacht. Des
Weiteren wurden alle Dioden in beiden Stromrichtungen untersucht. Zum Abschluss kam wider der bereits
bekannte Fön zum Einsatz, um qualitativ die Einwirkung von Wärme zu untersuchen.
Alle Kennlinien wurden von uns auf sie ausliegenden Formblätter übertragen. Daraus resultiert natürlich ein
gewisses Fehlerpotential, die für uns benötigte Genauigkeit ist jedoch absolut gegeben.
In allen Aufgabenteilen wurde darauf geachtet den Strom nicht zu groß zu wählen um die Dioden nicht zu
zerstören ( Durchbruchsstrom ).
3.1. Siliziumdiode (SID)
Als erstes untersuchten wir die klassische Siliziumdiode. Die Oszi-Bilder zeigten genau den zu erwartenden
Verlauf. ( Bild 2 des Bildprotokolls ) Während in der Sperrrichtung kein Strom durch die Diode hindurch kommt
ist der wesentliche Effekt in Durchlassrichtung zu betrachten. Hierbei ist gut zu beobachten, dass eine gewisse
Schwellenspannung erreicht werden muss, um die Diode von Sperren auf Durchlassen umzuschalten.
In unserem Fall liegt dieser Grenzwert bei ca. 0,6 Volt ( 6 Skalenteile bei 0,1 V pro Skalenteil ), was dem
erwarteten Wert entspricht.
IM Folgenden konnten wir bei einer Erwärmung der SID sehen, dass sich der Grenzwert verringert. ( gestrichelte
Linie im Bild )
3.2. Zenerdiode (ZED)
Bei der ZED sind nun beide Richtungen interessant. Dabei stellt die linke Seite des Bildes ( Bild 3 des
Bildprotokolls ) die Durchlassrichtung dar. Dabei ist der Grenzwert wieder bei ungefähr 0,6 Volt zu erkennen ( 3
Skalenteile bei 0,2 V pro Skalenteil ).
In der Sperrrichtung ( rechts im Bild ) ist deutlich ein Punkt zu erkennen, bei dem der Strom Sprunghaft ansteigt.
Dies ist der Punkt, bei dem der erwartete Zehnerdurchbruch stattfindet. Er liegt in unserem Fall bei ca. 6 Volt ( 3
Skalenteile bei 0,2 V pro Skalenteil ).
Eine Erwärmung führte nur zu einer Änderung des Grenzwertes in Durchlassrichtung. Analog zur SID sank er je
größer die Temperatur wurde. Auf den Punkt des Zehnerdurchbruchs hatte er keine Auswirkung.
3.3. Germaniumdiode (GED)
Die gefundene Kennlinie war bis auf den Grenzwert, bei dem die Diode auf „Durchlassen“ schaltete gleich der
Kennlinie der SID. Wie im Bild 4 des Bildprotokolls zu erkennen lag in diesem Fall jedoch die Grenzspannung
bei ca. 0,3 V ( 0,3 Skalenteile bei 1 V pro Skalenteil ).
In diesem Fall konnte bei einer Erwärmung keine Änderung beobachtet werden, was jedoch auch daran liegen
kann, dass wir eine relativ geringe Auflösung gewählt hatten.
Anmerkung: Im Bild stellt die grüne Skala die Sperrrichtung und rot die Durchlassrichtung dar.
3.4. Varistor (VDR)
Beim Auftragen der Kennlinie eines VDR erhielten wir, wie erwartet für beide Stromrichtungen ein
symmetrisches Bild. Dabei wurde der Stromfluss um so größer, je größer die angelegte Spannung war. Das sich
ergebende Bild ist in Bild 5 des Bildprotokolls wiedergegeben. Eine genauere Betrachtung der Werte erfolgt in
der nächsten Aufgabe.
Die Erwärmung des VDR führte zu keiner Reaktion.
Aufgabe 4. Punktuelle Messungen am Varistor
Im der nun folgenden Aufgabe betrachteten wir nochmals die Kennlinie eines Varistors. Diesmal jedoch, führten
wir eine Vielzahl von Einzelmessungen durch, um auf eine Funktion für den Strom in Abhängigkeit der
Spannung rückschließen zu können. Wir erwarten für diese Funktion einen Verlauf der Art
U = c*Ib
Ziel ist es nun durch geschicktes Auftragen die Konstanten für unseren VDR zu bestimmen. Hierzu gehen wir
wie in Aufgabe 1 vor und logarithmieren die Gleichung. Nun ergibt sich eine linearisierte Form deren
Konstanten über die Werte der Regressionsgeraden aus dem Schaubild gegeben sind.
ln(U ) = ln(c ) + b * ln( I )
Da in Aufgabe 3.4. bereits gezeigt wurde, dass sich der VDR für die beiden Stromrichtungen symmetrisch
verhält, wurde von uns, in dieser Aufgabe, nur eine Stromrichtung ausgemessen. Bei einer Variation der
Spannung erhielten wir folgende Ströme:
Spannung [ V ]
0,56
0,98
1,52
2,00
2,53
2,99
3,60
3,95
4,50
4,98
5,61
6,00
6,45
7,05
7,51
8,00
8,60
9,01
9,48
9,99
10,48
10,99
11,49
12,01
12,49
13,02
Strom [ A ]
4,00E-05
9,20E-05
2,10E-04
3,40E-04
4,60E-04
7,40E-04
1,10E-03
1,35E-03
1,82E-03
2,35E-03
3,20E-03
3,80E-03
4,30E-03
5,90E-03
7,00E-03
8,40E-03
1,00E-02
1,20E-02
1,40E-02
1,60E-02
1,90E-02
2,20E-02
2,60E-02
2,90E-02
3,40E-02
4,00E-02
ln (U)
-0,580
-0,020
0,419
0,693
0,928
1,095
1,281
1,374
1,504
1,605
1,725
1,792
1,864
1,953
2,016
2,079
2,152
2,198
2,249
2,302
2,349
2,397
2,441
2,486
2,525
2,566
ln(I)
-10,127
-9,294
-8,468
-7,987
-7,684
-7,209
-6,812
-6,608
-6,309
-6,053
-5,745
-5,573
-5,449
-5,133
-4,962
-4,780
-4,605
-4,423
-4,269
-4,135
-3,963
-3,817
-3,650
-3,540
-3,381
-3,219
VDR-Kennlinie
3
3
y = 0,4308x + 4,1081
ln ( U ) [ ln(V) ]
2
2
1
1
-11
-10
-9
-8
-7
-6
-5
-4
0
-1 -3
-1
ln ( I ) [ ln(A) ]
Dies ergibt für unsere Konstanten:
ln(c) = 4,108 → c = 60,831
b= 0,431
Dies führt uns auf eine Funktion der Form:
U ( I ) = 60,831Ω * I 0, 431
Im Vergleich zu Aufgabe 3.4. kann man sagen, dass es im Falle des Oszillographen möglich ist, schnell einen
Überblick über die gewünschte Kennlinie zu erhalten. Eine genauere Aussage über den genauen Verlauf lässt
sich jedoch mit der hier angewandten Methode treffen.
Aufgabe 5. Tunneldioden (GED)
5.1. Kennlinie einer GED
Es sollte nun die Kennlinie einer Tunneldiode aufgenommen werden. Hierzu verwendeten wir die in der
Aufgabenstellung geforderte Schaltung und führten punktweise eine Strom Spannungsmessung auf. Es war nun
die Aufgabe verschieden Größen aus der Messung herzuleiten und gegenüber der Spannung aufzutragen. Diese
Größen waren : Der Strom , der Widerstand , der differentielle Widerstand.
Dabei ergaben sich die Widerstände aus folgenden Formeln:
Widerstand
: R = U/I
Differentieller Widerstand
:
dU U 2 − U 1
=
dI
I 2 − I1
Für die Messwertetabelle ergaben sich somit folgende Werte:
Spannung [ V] Strom [ A ] Widerstand [ Ω ]
0,400
7,00E-05
5714
0,380
4,80E-05
7917
0,360
3,20E-05
11250
0,340
2,80E-05
12143
0,320
2,20E-05
14545
0,300
2,00E-05
15000
0,280
1,90E-05
14737
0,270
1,89E-05
14286
0,260
1,90E-05
13684
0,240
2,00E-05
12000
0,220
2,10E-05
10476
0,200
2,40E-05
8333
0,180
2,90E-05
6207
0,160
3,30E-05
4848
0,140
4,20E-05
3333
0,120
6,50E-05
1846
0,100
7,20E-05
1389
0,080
8,40E-05
952
0,060
1,10E-04
545
0,040
1,15E-04
348
0,020
8,50E-05
235
0,010
5,00E-05
200
0,005
3,00E-05
167
0,000
2,00E-06
0
dU/dI [ Ω ]
0,909
1,250
5,000
3,333
10,000
20,000
100,000
-100,000
-20,000
-20,000
-6,667
-4,000
-5,000
-2,222
-0,870
-2,857
-1,667
-0,769
-4,000
0,667
0,286
0,250
0,179
0,000
Diese Messdaten in Schaubildern ausgedrückt ergaben folgende Graphen:
GED- Strom
1,40E-04
1,20E-04
I[A]
1,00E-04
8,00E-05
6,00E-05
4,00E-05
2,00E-05
0,00E+00
0,000
0,100
0,200
0,300
0,400
0,500
0,400
0,500
U[ V ]
GED- Widerstand
16000
14000
R[Ω]
12000
10000
8000
6000
4000
2000
0
0,000
0,100
0,200
0,300
U[ V ]
GED- differentieller Widerstand
150,000
100,000
dU/dI [ Ω ]
50,000
0,000
0,000
-50,000
0,100
0,200
0,300
0,400
0,500
-100,000
-150,000
U[ V ]
In den Schaubildern ergibt sich eine gute Übereinstimmung mit den in der Aufgabenstellung erwähnten
Erwartungswerten von Höcker und Talpunkt.
5.2. Sprungverhalten des Stromes
Wir stellten das Amperemeter auf den Bereich 100µA und fingen an, die Spannung langsam von Null ab
hochzuregeln. Wir konnten beobachten, dass die Anzeige des Stromes bei einem Wert außerhalb des
Anzeigenbereichs Sprunghaft auf 25µA sprang. Regelten wir die Spannung in die andere Richtung konnte
festgestellt werden, dass die Anzeige von dem Wert 30µA auf einem Wert außerhalb des Anzeigenbereichs
Zurücksprang.
Die Erklärung dieses Phänomens liegt in der Tatsache begründet, dass bei dem gewählten Messbereich die
Innenwiderstände des Geräts so geartet sind, dass die Arbeitsgerade des Geräts die Kennlinie der Tunneldiode
mehrfach schneidet. Der Strom kann entlang dieser Arbeitsgeraden sozusagen „abkürzen“ und zwischen den
Schnittpunkten Springen.
Schneidet die Arbeitsgerade die Kennlinie nur einmal, kann dies nicht geschehen.
Im Folgenden haben wir die Arbeitsgerade in das Diagramm miteingezeichnet um die Schnittpunkte zu
verdeutlichen. Dabei ergibt sich die Arbeitsgerade zu :
I=
U0 −U
R
Da das alte Messgerät nicht mehr funktionierte, erhielten wir ein neues Messgerät, dessen Kenndaten wir leider
nicht kennen. Wir verwendeten daher die Kenndaten des alten Geräts um die Arbeitsgerade im Schaubild
sichtbar zu machen. ( R=1700 ).
Wir folgten nun dem Schaubild von 0V ab und verschoben die Arbeitsgerade so parallel, dass sie immer durch
den beobachteten Punkt verlief. Nun suchten wir genau den Punkt, bei dem die Gerade das Schaubild zum ersten
Mal doppelt schnitt. Es zeigte sich, dass die Schnittpunkte bei ca. 110µA ( außerhalb des Anzeigebereichs ) und
30µA liegen, was unseren gemessenen Werten entspricht.
Auch auf dem umgekehrten Weg von hohen Spannungen ab verfuhren wir so und kamen auf Schnittpunkte im
Bereich 25µA und 120µA (außerhalb des Anzeigebereichs ). Auch diese Werte liegen im Bereich unserer
Messung.
GED- Strom
2,00E-04
1,50E-04
von 0,4V kommend
I[A]
1,00E-04
5,00E-05
0,00E+00
0,000
0,050
0,100
0,150
0,200
0,250
0,300
0,350
0,400
0,450
-5,00E-05
-1,00E-04
von 0V kommend
-1,50E-04
U[ V ]
Die Sprünge sind nur bei kleinen Messbereichen zu erwarten, da bei größeren Skalen der Innenwiderstand so
geartet ist, dass die arbeitsgerade sehr steil wird und die Kennlinie nicht mehr mehrfach schneidet.
5.3 Spannungsüberhöhungen
In diesem letzten Versuchsteil wurde im Vergleich zur vorangehenden Aufgabe noch eine Spule in die Schaltung
integriert. Sie Spannung wurde nun langsam erhöht und der Stromverlauf über einen Oszillographen beobachtet.
Es wurde nun genau der Punkt des Springens abgepasst, der sich durch eine Schwingung auf dem Oszi-Schirm
darstellt.
Diese Schwingung beruht darauf, dass die Spule auf die plötzliche Stromänderung derart reagiert, dass sie eine
Gegenspannung induziert. Dabei löst sie jedoch einen Sprung in die Rückrichtung aus was ihr eine Reaktion in
die Gegenrichtung entlockt, wodurch wieder der ursprüngliche Sprungpunkt erreicht wird. Dieser Prozess setzt
sich fort und führt zu der beobachteten Schwingung.
Wir verwendeten nun zwei verschieden Spulen und bestimmten jeweils die Frequenz der beobachteten
Schwingungen.
Spule 1 : F= 47µH
5 ½ Schwingungen auf 7 Skalenteilen
0,2µs pro Skalenteil
→ 3,929 MHz
Spule 2 : F= 330µH
5 Schwingungen auf 7 Skalenteilen
0,5µs pro Skalenteil
→ 1,429 MHz