Kein Folientitel - Datenbanksysteme und Wissensbasen
Werbung

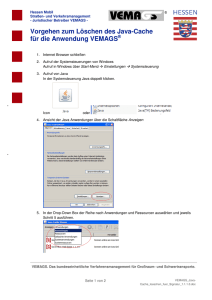
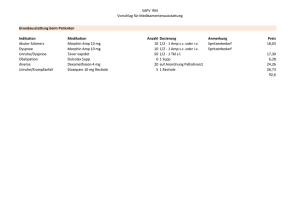
R-Bäume: eine dynamische Indexstruktur für räumliches Suchen Forschungs- und Lehreinheit Informatik III - Datenbanksysteme und Wissensbasen Vortrag über R-Bäume in der Reihe ‚Algorithmen und Datenstrukturen für Datenbanksysteme‘ Proseminar Informatik im SS 2001, Prof. Dr. D. Kossmann Vortragender: Florian Sager Konfiguration, Aufbau eines R-Baumes c2 c3 c1 c5 c9 c6 c4 c1 c2 c3 c4 c5 c8 c9 c10 c11c12 c7 c11 c10 c12 c8 c6 c7 Bildung von n-dimensionalen Hüllen (=Rechtecke im 2-D, Quader im 3-D etc.) der tatsächlichen, räumlichen Objekte, sog. nRects. Formale Darstellung von nRects: (int_0, int_1, ... int_(n-1)) int_* ist ein Intervall in der entsprechenden Dimension Idee: Bildung von geeigneten Partitionen (M=3) a1 a2 b1 b2 b3 a1 b1 b2 c1 b4 c5 c9 b3 c2 c3 a2 c4 c6 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10c11c12 c7 c11 b5 c10 c12 c8 b4 b5 Zusammenfassen von maximal M ‚benachbarten‘ nRects in eine gemeinsame, umschließende Hülle. Fortführung durch die Gruppierung der in den einzelnen Schritten resultierenden nRects bis zur maximal möglichen Zusammenfassung Knoten und Blätter des R-Baumes M: max. Anzahl an Einträgen eines Knotens m: min. Anzahl an Einträgen eines Knotens M m a1 a2 nRect child-ptr nRect ID b1 b2 b3 c1 c2 c3 c4 c5 b4 b5 c6 c7 c8 c9 c10c11c12 Verweise über IDs auf ‚spatial data‘, bsp. einzelne Sätze in einer Datenbank Suche in R-Bäumen a1 a2 b1 b2 b3 a1 b1 b2 c1 c5 b4 c9 b3 c2 c3 a2 c4 c6 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10c11c12 c7 c11 b5 c10 c12 c8 b4 b5 k sei die Baumhöhe. Worst-Case: k 1 M M M 1 M 2 ... M k M 1 Best-Case: m*k NN Suche in R-Bäumen Welche Box liegt diesem Punkt am nächsten? a1 a2 b1 b2 b3 a1 b1 b2 b3 c2 c3 c1 c5 a2 b4 b5 c4 c6 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10c11c12 c7 c11 b5 Branch & Bound Algorithmus 1. Starte an der Wurzel b4 c9 c10 2. Bewerte Abstand jeder BB c12 c8 3. Tiefensuche 4. Pruning mit jedem Ergebnis Einfügen in R-Bäumen: Schritt 1 a1 a2 b1 b2 b3 a1 b1 b2 c1 b4 c5 c9 b3 c2 c3 a2 c4 c6 c1 c2 c3 c4 c5 c6 c7 c8 c9 c10c11c12 c7 c11 b5 c10 c12 c8 b4 b5 Suchen des Eintrags, dessen nRect am wenigsten erweitert werden muß, um das neue nRect aufzunehmen. Wiederholung auf k-1 Ebenen. Im Beispiel: Knotensplit notwendig Einfügen in R-Bäumen: Schritt 2 Einfügen des Eintrags in das gef. Blatt. Wird die Anzahl M der Einträge im Blatt überschritten, wird ein Knotensplit vorgenommen. c11 b5 c11 b5 c10 b6 c12 c12 c13 c13 b4 b5 c8 c9 c10 c10c11c12 b4 b5 b6 c8 c9 c11c12 c10c13 Einfügen in R-Bäumen: Schritt 3 Anpassung aller übergeordneten nRects im Baum, sofern die Aufnahme des neuen Eintrags eine Erweiterung erfordert. Überblick: a1 a2 b1 b2 b3 c1 c2 c3 c4 c5 b4 b5 b6 c6 c7 c8 c9 c11c12 c10c13 Löschen in R-Bäumen (1) Aufsuchen des zu löschenden Eintrags im Baum (2) Falls vorhanden, Eintrag löschen und Parent-nRect ggf. angleichen (3) Sinkt dadurch die Anzahl der Einträge im betreffenden Knoten unter m, werden alle verbleibenden Einträge in einer Queue zwischengespeichert. Der Knoten ist dadurch aufgelöst, das Parent-nRect muß angeglichen werden. (4) Fortführung des Zusammenlegens von Knoten auf höheren Ebenen nach gleichem Schema, sofern notwendig (5) Neuaufnahme aller in der Queue zwischengespeicherten Einträge per Insert-Operation a1 a2 b1 b2 b3 c1 c2 c3 c4 c5 b4 b5 b6 c6 c7 c8 c9 c11c12 c10c13 Updates in R-Bäumen Im R-Baum zu berücksichtigen ist die Veränderung des nRects eines Objekts. • Vor der Veränderung wird der Eintrag per Delete-Operation aus dem Baum gelöscht, • die Veränderung am nRect vorgenommen • und das Objekt per Insert-Operation neu in den Baum eingefügt. Partitionierungsverfahren Thema Suche des günstigsten Verfahrens, um M+1 Einträge auf zwei Knoten zu verteilen: • günstig im Sinne der Aufwandsminimierung bei der Verteilung • und der Herstellung von ‚geeigneten Aufteilungen‘ für eine effiziente Baumstruktur Beispiel für Aufteilungsmöglichkeiten Keine Überlappung, große Fläche größere Trefferwahrscheinlichkeit einer Suchabfrage, größere Wahrscheinlichkeit des Abbruchs der Suche auf niedriger Ebene im Baum Geringe Fläche, mit Überlappung zwangsläufige Verfolgung von mehreren (=2) Pfaden bei der Suche innerhalb der Überlappung Partitionierungsverfahren: Überlappungen und Ausmaße (M=3) a1 a2 b1 b2 b3 a1 b1 b2 c1 b4 c5 c9 b3 c2 c3 a2 c4 c6 c1 c2 c3 c4 c5 c7 c11 b5 c10 c12 c8 b4 b5 c6 c7 c8 c9 c10c11c12 Partitionierungsverfahren Folgerung Neben der Wahl von m und M (minimale und maximale Anzahl der Einträge in einem Knoten des R-Baumes) bieten die Partitionierungsverfahren Möglichkeiten zur Optimierung der Effizienz der Indexstruktur. Partitionierungsverfahren: Verfahren mit exponentiellem Aufwand im R-Baum Suche diejenige Aufteilung, in der das eingenommene Volumen minimal ist, über die Berechnung in allen möglichen Aufteilungen. Anzahl der Aufteilungsmögl. bei i=M+1: i i i ... m m 1 lowG (i / 2) Weitere Partitionierungsverfahren Verfahren mit quadratischem Aufwand im R-Baum (1) Suche diejenigen nRects, die zusammen in einer der beiden Gruppen die größte Fläche einnehmen würden (quadr. Aufwand). Sie bilden jeweils den ersten Eintrag einer der beiden neuen Gruppen. (2) Ordne jedes weitere nRect derjenigen Gruppe zu, in der es unter der geringsten Flächenerweiterung aufgenommen werden kann. Verfahren mit linearem Aufwand im R-Baum Suche von maximalen Aufteilungen in einzelnen Dimensionen (...) Optimierungen und Weiterentwicklungen der Partitionierungsverfahren R*-Bäume Idee: Berücksichtigung von • Volumen • Überlappungsgrad • Seitenlängenverhältnis zum Auffinden der optimalen Partitionierung R+-Bäume Idee: Vermeidung der Überlappung einzelner nRects über die Aufteilung der Objekt-nRects in mehrere, disjunkte Teile. Test-Auswertung Vergleich von R-Baum und R*-Baum: Punktsuche Überschneidung 0,01 0,1 0,001 qua. Gut 147 153 143 132 116 159 R*-Baum 100 100 100 100 100 # I/O 4,78 5,29 7,35 14,65 60,84 1,0 Enthaltensein 0,001 0,01 ändern einfügen 160 68 5 100 100 71 4 4,08 3,08 Zusammenfassung R-Bäume: eine dynamische Indexstruktur für räumliches Suchen • Idee: Bildung von Partitionierungen • Optimierungen über die Veränderung des Partitionierungsverfahrens • oder die Wahl der Anzahl der Einträge in den Knoten (M und m) • besonders geeignet für die Indizierung von räumlichen Objekten mit ähnlicher Größe und, im Ideal, quadratischer Form.