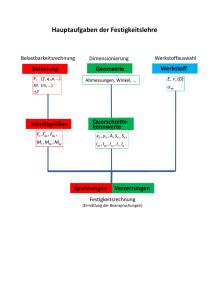
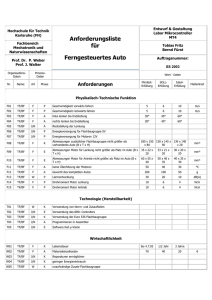
Mechanik deformierbarer Medien
Werbung

Mechanik deformierbarer Medien Scherung, Torsion, Hysterese Inhalt • Elastische Auslenkungen außer der Dehnung: – Scherung – Torsion • „Elastische Nachwirkung“: Hysterese Voraussetzung der Elastizität: Feder-Modell für kleine Auslenkungen Schubelastizität Fläche Scherwinkel A Scherkraft F Die Kraft wirkt tangential zur Angriffsfläche Scherung eines quaderförmigen Körper, an dessen oberer Fläche – senkrecht zur Flächen-Normalen - eine Kraft angreift Versuch: Scherspannung und Scherung Schubspannung und Scherungsmodul Einheit G 1 N/m2 Schubspannung und Scherwinkel F A 1 N/m2 Schubspannung 1 Scherwinkel G 1 Schub- Scherungsoder Torsionsmodul „Der Scherwinkel ist proportional zur Scherkraft“ R a d i u s Schubspannung und Scherungsmodul am zylindrischen Stab Scherspannung Radius R l Scherwinkel α Torsion eines unten eingespannten zylinderförmigen Körpers, an dessen oberer Fläche eine Scherkraft angreift wirkt Schubspannung und Scherungsmodul Einheit G 1 N/m2 Schubspannung und Scherwinkel F A 1 N/m2 Schubspannung 1 Scherwinkel G 1 Schub- Scherungsoder Torsionsmodul „Der Scherwinkel ist proportional zur Scherkraft“ Drehmoment bei Torsion F r T R a d i u s Drehmoment und Torsionswinkel Torsionswinkel Drehmoment Radius T R l Torsion eines unten eingespannten zylinderförmigen Körpers, auf den ein Drehmoment bezüglich der Zylinderachse wirkt Schubspannung und Scherungsmodul am zylindrischen Stab Einheit l T 4 GR 1 Drehmoment und Torsionswinkel T F r 1 Nm Drehmoment 1 Drehwinkel G 1 N/m2 Schub- Scherungsoder Torsionsmodul R l 1m Radius des Stabs 1m Länge des Stabs 2 „Der Scherwinkel ist proportional zur Scherkraft“ Versuch: Torsion eine Stabes Versuch: Torsionspendel Hysterese • Zusätzlich zur Elastizität, dem „Federmodell“ für kleine Auslenkungen, erscheinen • bleibende Veränderungen durch – Fließen oder – Änderung des kristallinen Gefüges oder – Änderung der Orientierung länglicher Moleküle Elastizität und Fließen Hysterese • Bleibende Veränderung nach der Kraft-Einwirkung – Eine „rückstellende Kraft“ ist erforderlich, um den AusgangsZustand wieder herzustellen und zu erhalten (!) Hysterese-Kurve Kraft Auslenkung Hysterese-Kurve • Bleibende Veränderung nach der Kraft-Einwirkung – Eine „rückstellende Kraft“ ist erforderlich, um den AusgangsZustand wieder herzustellen und zu erhalten (!) „Neukurve“ bei erstmaliger Belastung Kraft Auslenkung Weg-Kraft Verlauf der „Neukurve“, d. h. bei erstmaliger Anwendung, wird nicht wieder erreicht Zusammenfassung • Scherung: – Der Scherwinkel ist proportional zur Scherkraft • Torsion: – Der Drehwinkel ist proportional zum Drehmoment – Der Drehwinkel ist umgekehrt proportional zur vierten Potenz des Radius • Hysterese: – Bleibende Veränderung nach der Kraft-Einwirkung • Eine „rückstellende Kraft“ ist erforderlich, um den AusgangsZustand wieder herzustellen • Weg-Kraft Verlauf der „Neukurve“, d. h. beim erstmaliger Anwendung, wird nicht wieder erreicht Finis