Hauptaufgaben der Festigkeitslehre - georgi

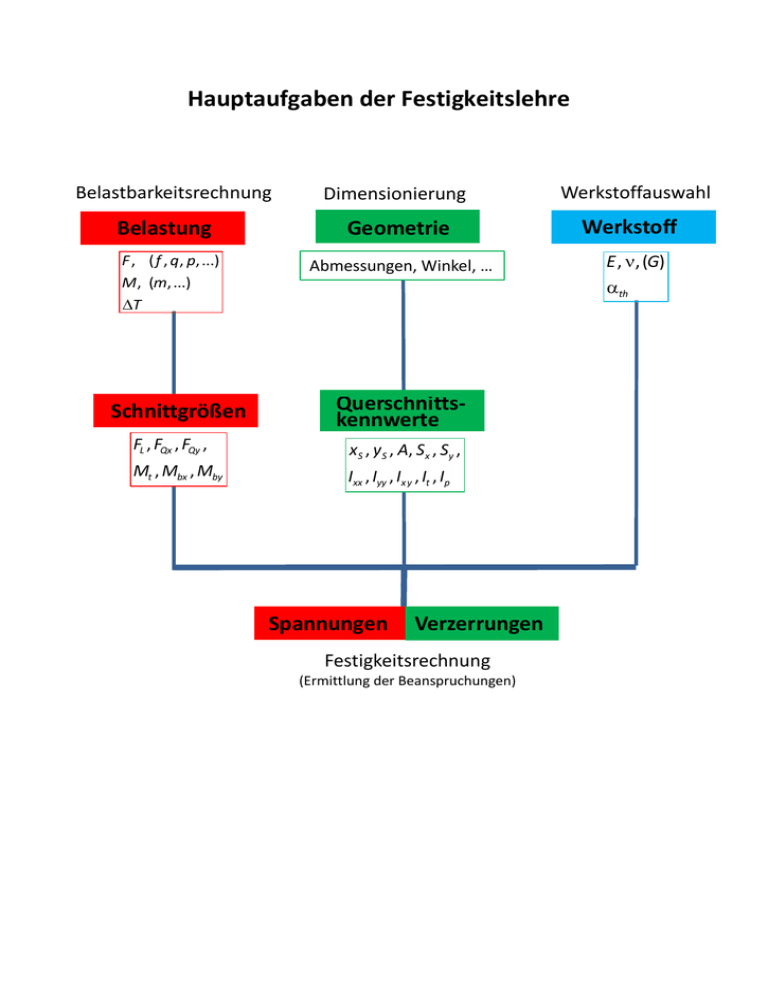
Hauptaufgaben der Festigkeitslehre
Belastbarkeitsrechnung
Belastung
F , ( f , q , p, ...)
M , (m, ...)
T
Schnittgrößen
Dimensionierung
Werkstoffauswahl
Geometrie
Werkstoff
Abmessungen, Winkel, …
Querschnittskennwerte
FL , FQx , FQy ,
xS , yS , A, Sx , Sy ,
Mt , Mbx , Mby
Ixx , Iyy , Ix y , It , Ip
Spannungen
Verzerrungen
Festigkeitsrechnung
(Ermittlung der Beanspruchungen)
E , , (G)
th
10
Formelsammlung Technische Mechanik
Schnittgrößen beim Balken
Definition
M by
M bx
F Qy
S
FL
z M
t
x
y
F Qx
FQx
S FL
FQy
Mt
M bx
dz
M by
oder:
M bx
Mt
FL S
F Qx
S FQy
F Qx F L
FQy
M by
M by
M bx
dz
Mt
x
z
y
mit: FL
- Längskraft
FQx , FQy - Querkräfte
Mbx , Mby - Biegemomente
Mt
- Torsionsmoment
Achsen x, y, z bilden körperfestes Rechtssystem
z- Achse entlang der Schwerpunktsachse, zeigt bei
größerem Koordinatenwert aus Querschnitt heraus
y-Achse zeigt nach unten
Beanspruchungsart
Zug/Druck (Indizes z/d)
Voraussetzungen: Gültigkeit des Prinzips von de Saint Venant
Keine Volumenkräfte
Maßgebliche Schnittgröße: Längskraft
FL= F= konst .
Definition Dehnungen:
ε zz= uz,z=
∆lz
lz
ε xx= u x,x=
∆lx
lx
ε yy= uy ,y=
∆ly
ly
HOOKEsches Gesetz:
ε zz=
ε xx
ε yy
1
σzz + α ∆T
E
ν
= − σzz + α ∆T
E
ν
= − σzz + α ∆T
E
Äquivalenz (bzw. Gleichgewicht ) :
σzz A =
FL
Verzerrungen (Dehnungen):
ε=
zz
ε xx
ε yy
FL
+ α ∆T
EA
F
= −ν L + α ∆T
EA
F
= −ν L + α ∆T
EA
Spannung:
σzz = σ =
FL
A
EA
Dehnsteifigkeit
Beanspruchungsart
Torsion (Index t)
Voraussetzungen: Reine Torsion
Kreis(ring)querschnitt
Maßgebliche Schnittgröße: Torsionsmoment
M=
M
= konst .
t
Geometrie:
γ ϕz dz =
r dϕ
Definition Drillung:
=
ϑ
dϕ ϕ
=
dz l
γ ϕz =
ϑr
HOOKEsches Gesetz:
τϕz
γ ϕz = =
ϑr
G
Äquivalenz (bzw. Gleichgewicht ) :
Mt =
G
∫ r τϕz dA =
∫ r G ϑ r dA =ϑ
( A)
( A)
∫r
2
dA
( A)
Definition Polares Flächenträgheitsmoment:
Ip =
∫r
2
dA
( A)
Verzerrung (Drillung):
ϑ=
Mt
G Ip
GIp
Torsionssteifigkeit
Spannung:
τϕz = τt = τ =
Mt
r
Ip
Mt
τ max =max
Wp
Wp =
Ip
ra
Wp Polares Widerstandsmoment:
50
Formelsammlung Technische Mechanik
Trägheits- und Widerstandsmomente gegenüber
Torsion
It
Wt
 4
Ra  Ri4  

2

Da4  Di4 

32
 Ra4  Ri4

2 Ra
Querschnitt
Kreis (Ri=0),
Kreisring
Di=2Ri
 Da4  Di4
16
Da
Da=2Ra
It
1 n
li 3i

3 i 1
( s
)
dünnwandig
offen
s
dünnwandig
geschlossen

i max
4 Am2
1
ds
( s )
2 Am min
Am
c1 h b3
h
Rechteck
(h>b)
b
h/b
1
c2 h b2
1,5
2
3
4
c1
0,141 0,196 0,229 0,263 0,281
c2
0,208 0,231 0,246 0,267 0,282