Wechselstrom
Werbung

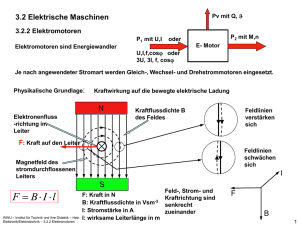
3. Einführung in die Elektrotechnik 3.1 3.2 3.3 3.4 3.5 Grundlagen der Wechselstromtechnik Elektrische Maschinen Beleuchtungstechnik Energieversorgungssystem Übungen zur Elektrotechnik WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 1 3.1 Wechselstromlehre Das Verhalten von Spulen und Kondensatoren bei Wechselstrom Spulen bestehen aus elektrischen Leitern, die meistens zylindrisch aufgewickelt sind. Durch das Aufwickeln des Leiters treten Eigenschaften zutage, die beim gestreckten Leiter so nicht zu beobachten sind. Um diese Eigenschaften geht es im folgenden. Wie wir bereits wissen, ist jede gerichtete elektrische Strömung von einem Magnetfeld begleitet. Dieses kann man sich als konzentrische Zylinder, die um den Leiter geschichtet sind, vorstellen. Da magnetische Felder sinnlich nicht wahrnehmbar sind, benutzt man zur besseren Vorstellung ein Modell, das der Feldlinien. I Die Richtung des Feldes ist folgendermaßen festgelegt: Wenn der Strom in den Leiter hinein fließt, wie es der Pfeil anzeigt, dann umgibt das Feld den Leiter so, daß die Richtung des Feldes der Uhrzeigerrichtung gleich ist. Die Richtungspfeile der Feldlinien zeigen das im Bild. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 2 Wird der Leiter zu einer Spule gewickelt, dann entsteht eine Feld anderer Art. S I I N = 1 V s = 1 Wb (1 Weber) Dieses Feld ist ein resultierendes Feld und dem eines stabförmigen Dauermagneten sehr ähnlich. Es entsteht durch die Vereinigung der vielen konzentrischen Feldlinien um den jetzt zu einer Spule gewickelten Leiter. Die gesamte Erscheinung der magnetischen Feldlinien bezeichnet man als magnetischen Fluss . Die Bezeichnung Fluss ist insofern nicht korrekt, weil in Wirklichkeit hier nichts fließt. Aber auch dieser Begriff ist heute nicht mehr zu ändern und muss so akzeptiert werden. Eine weitere wesentliche Größe ist die Kraftflußdichte oder magnetische Induktion B. B d dA Für homogene Magnetfelder, wie sie im Inneren von Spulen zu finden sind, gilt dann: WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik B = 1 Wb/m2 = 1 T B (1 Tesla) A 3 Das Durchflutungsgesetz Analog zum elektrischen Strom als Strömungsgröße existiert auch für den magnetischen Fluss als Strömungsgröße eine Antriebsgröße. Diese Antriebsgröße wird als magnetische Urspannung oder Durchflutung bezeichnet. Den Zusammenhang zwischen der Stromstärke, der Windungszahl N einer Spule und der Durchflutung beschreibt das Durchflutungsgesetz. I N []= 1 A Magnetischer Widerstand Analog zum elektrischen Stromkreis wird der magnetischen Kreis betrachtet. Zur magnetischen Urspannung als Antriebsgröße und dem magnetischen Fluss als Strömungsgröße gehört dann der magnetische Widerstand Rm. Magnetische Kreise bestehen in der Regel aus Eisen, oft allerdings mit einem oder mehreren Luftspalten. Dieses Eisen und vor allem die Luftspalte setzen dem magnetischen Fluss einen Widerstand entgegen. Das Maß für die Leitfähigkeit des magnetischen Flusses ist die Permeabilität . Eisen leitet den magnetischen Fluss etwa 700 mal besser als Luft. I Für den magnetischen Widerstand eines magnetischen Kreises gilt: Rm l A l: Länge der Feldlinien A: Querschnitt des Eisenkernes I WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 4 Analogie zwischen elektrischem Kreises und magnetischen Kreis: I I UO U I R U I R l A l Rm A Rm 1 elektrische Grösse Einheit Magnetische Grösse Einheit elektrische Spannung U 1V 1A elektrische Stromstärke (es fliessen Ladungsträger) 1A Durchflutung (magn. Urspannung) magnetischer Fluss (es fliesst nichts) elektrischer Widerstand R = l/*A 1 magnetischer Widerstand Rm =l/ *A 1 A/Vs Elektrische Leitfähigkeit A/Vm magnetische Leitfähigkeit Vs/Am WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 1 Ws; 1Wb 5 Das Induktionsgesetz Während das Durchflutungsgesetz die Erzeugung von Magnetfeldern durch elektrische Ströme beschreibt, modelliert das Induktionsgesetz den in entgegengesetzter Richtung verlaufenden Vorgang, die Erzeugung elektrischer Spannung durch sich ändernde magnetische Felder. In einem Leiter werden immer dann elektrische Spannungen u0 induziert, wenn er einem sich ändernden Magnetfeld ausgesetzt ist. Für ein Leiterschleifensystem mit N Windungen der Induktionsspule gilt: u0 N d dt Die induzierte Spannung hat folgende Eigenschaften: 1. ihr Betrag ist abhängig von der Windungszahl N 2. ihr Betrag ist abhängig von der Änderungsgeschwindigkeit des Kraftflusses d/dt 3. die Induktionswirkungen sind so gerichtet, daß sie ihrer Ursache, der Feldänderung also, stets entgegengerichtet sind ! Dieser Zusammenhang ist als LENZsche Regel bekannt und spielt beim Verständnis der weiteren Zusammenhänge eine große Rolle. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 6 Das Induktionsgesetz wirkt in zwei Zusammenhängen, nämlich 1. bei der Selbstinduktion (Selbstinduktion tritt in jeder stromdurchflossenen Spule selbst auf, wenn sich in ihr der magnetische Fluß infolge von Stromstärkeänderung ebenfalls ändert.) 2. bei Gegeninduktion. (Zur Gegeninduktion ist immer eine 2. Spule erforderlich, die allerdings nicht ursächlich von einem Strom durchflossen wird, wohl aber einem sich ändernden Magnetfeld ausgesetzt ist.) Zur Erklärung des Verhaltens von Spulen im Wechselstromkreis genügt es, Selbstinduktion zu betrachten. Durchfließt ein sich zeitlich ändernder Strom i(t) die Spule eines magnetischen Kreises, so folgt diesem eine sich zeitlich ändernde Durchflutung (t), die ihrerseits einen sich zeitlich ändernden magnetischen Fluß (t) nach sich zieht. Es gilt dann: (t ) (t ) N i (t ) Rm Rm Wie vorangestellt, induziert dieser sich zeitlich ändernde Fluß in der Spule eine Induktionsspannung u0. d ( t ) di N 2 di u0 N N N N dt Rm dt Rm dt Rm dt Die Größen N2/ Rm sind konstruktive Eigenschaften der Spule und werden als Induktivität L bezeichnet. Somit gilt für die Selbstinduktionsspannung einer Spule: u0 L di dt WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 7 Die wesentlich Frage ist nun, wie die Selbstinduktionsspannung in der Spule zu verstehen ist und welche Wirkung die Entstehung der Selbstinduktionsspannung für das Verhalten der Spule hat. Dazu dient folgender Gedankenversuch. A U i ui V t1 t2 Die Überlegungen lassen offensichtlich werden, daß, wenn nach dem Abschalten der Stromstärke aus der Energiequelle eine Spule weiterhin Strom in den Stromkreis speist, diese in der Lage sein muss, Energie zu speichern. Das ist auch so. Spulen Speichern Energie in Form ihres magnetischen Feldes. Das Speichervermögen einer Spule ist von ihrer Induktivität und der aktuellen Stromstärke abhängig. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik t Wmag I2 L 2 8 Kehren wir zurück zum zeitlichen Verhalten von Strom und Spannung an Spulen. Das Diagramm veranschaulicht, dass bei Schaltvorgängen an Spulen der Strom im zeitlichen Nachlauf zur Spannung ansteigt bzw. abfällt. Man sagt, „die Spannung eilt dem Strom voraus“ oder „der Strom eilt der Spannung nach“. Merke: 1. Veränderliche Ströme in Spulen erzeugen Induktionsspannungen. 2. Diese Induktionsspannungen sind ihrem ursächlichen Strom entgegengerichtet und wirken auf diesen wie Widerstände. 3. Die Spannungen eilen den Strömen voraus. 4. Spulen speichern Energie in Form magnetischer Felder. Die Strom-Spannungsbeziehung der Spule lautet: WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik u0 L di dt 9 Kondensatoren Spulen speichern Energie in Form des magnetischen Feldes. Kondensatoren speichern Energie in Form des elektrischen Feldes. Das Speichervermögen eines Kondensators wird als Kapazität C bezeichnet. A C d A: Flächeninhalt der Kondensatorplatten d: Abstand der Platten zueinander : Dielekrikumskonstante ( Leitfähigkeit für das elektrische Feld) Analog zur Spule wird dann die im Kondensator gespeicherte Energie: Gedankenexperiment Welek U2 C 2 zum Verhalten des Kondensators: u i R A V t1 t2 t3 t -i WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 10 Merke: 1. Veränderliche Spannungen erzeugen an Kondensatoren Ströme mit zeitlich verändertem Verhalten. 2. Die Ströme eilen den Spannungen voraus. 3. Kondensatoren speichern Energie in Form elektrischer Felder. Die Strom-Spannungsbeziehung am Kondensator lautet: WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik i C dU dt 11 Das Verhalten von Widerständen, Spulen und Kondensatoren im Wechselstromkreis Technischer Wechselstrom, hochfrequente elektromagnetische Strahlungen und viele niederfrequente und elektroakustische Verfahren werden als Schwingungsvorgänge beschrieben, die mit der Sinusoder Cosinusfunktion abgebildet werden können. Entstehung von Einphasenwechselspannung u (t ) umax sin( t ) i(t ) imax sin( t ) Erläuterungen WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 2 f 12 Ohmscher Widerstand im Wechselstromkreis Liegt Wechselspannung an einem Ohmschen Widerstand, dann wird der Augenblickswert der Stromstärke durch das Ohmsche Gesetz bestimmt. Ohmsche Widerstände sind z.B. Glühlampen, Heizgeräte, Bügeleisen und Toaster. I u (t ) umax (sin t ) imax (sin t ) R R imax mit u max R Aus der Gleichung ist erkennbar, daß Strom und Spannung zeitlich übereinstimmen, man sagt, “es gibt keine Phasenverschiebung” und somit ist der Rhasenverschiebungswinkel = 0. u i i u R u i t Dieser Sachverhalt wird auch mit dem Zeigerdiagramm ebenso wie mit dem Liniendiagramm verdeutlicht. Widerstände dieser Art werden im Wechselstromkreis als Wirkwiderstände bezeichnet. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 13 Kondensator im Wechselstromkreis Bei angelegter Wechselspannung ergibt sich für den Strom am Kondensator: i C du sin( t ) dU C max dt dt und nach Differenzierung i C umax cos( t ) C umax sin( t ) 2 Im Vergleich mit u (t ) umax (sin t ) zeigt sich, daß am Kondensator der Strom gegenüber der Spannung um /2 , d.h. um eine viertel Periode vorauseilt. u i i i u C 2 WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik u 2 3 2 2 t 14 Aus der Gleichung i C umax cos( t ) der Strom ein Maximum hat, woraus folgt, dass ergibt sich, dass für t 0 imax C umax gilt. Schreibt man beide Maximalwerte als Widerstand auf, so ergibt sich: u max 1 Xc imax C Xc ist der im Wechselstromkreis wirksame Widerstand des Kondensators und wird als kapazitiver Blindwiderstand bezeichnet. Analog gilt für den Leitwert: Merke: Y 1 XC 1. Kondensatoren verursachen im Wechselstromkreis eine theoretische Phasenverschiebung zwischen Strom und Spannung von /2 oder 90 2. Der Strom eilt der Spannung voraus. 3. Es wirkt der kapazitive Blindwiderstand Xc. 4. Mit steigender Frequenz wird wegen Xc = 1/2 f C der Blindwiderstand geringer. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 15 Spule im Wechselstromkreis Für eine ideale Spule gilt: u(t) + u0 = 0 Erklärung umax (sin t ) L di 0 dt beide Spannungen eingesetzt umax nach di aufgelöst sin tdt L u u i (t ) max cos t max (sin t ) L L 2 di nach Integration Im induktiven Blindwiderstand eilt die Stromstärke der Spannung um /2 , also eine Viertel Periode nach. u i i u L i 2 WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik u 2 3 2 2 t 16 Aus der Gleichung u i max cos( t ) L der Strom ein Maximum hat, woraus folgt, dass ergibt sich, dass für imax u max L t 2 gilt. Schreibt man beide Maximalwerte als Widerstand auf, so ergibt sich: umax L XL imax Der induktive Widerstand XL einer Spule ist der Frequenz proportional. Merke: 1. Spulen verursachen im Wechselstromkreis eine theoretische Phasenverschiebung zwischen Strom und Spannung von -/2 oder -90 2. Der Strom eilt der Spannung nach. 3. Es wirkt der induktive Blindwiderstand XL. 4. Mit steigender Frequenz wird wegen XL = 2 f L der Blindwiderstand größer. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 17 Im vorangegangenen Teil haben wir uns zu eigen gemacht, daß Spulen und Kondensatoren bei veränderlichen Stromstärken und Spannungen ein spezifisches Verhalten haben. Sie kennen dieses Verhalten und können die Ursachen und ihre Wirkungen erklären. Wir sind weiterhin davon ausgegangen, daß die Spulen und Kondensatoren ideale Bauelemente sind, dh. das Leitermaterial der Spulen hat keinen elektrischen Widerstand, das Dielektrikum der Kondensatoren hat einen unendlich großen elektrischen Widerstand. Daß dies eine idealisierte Modellvorstellung ist, die der Vereinfachung der Erklärung der Vorgänge dient, soll nun noch einmal deutlich gesagt werden. In der Wirklichkeit ist es so, daß sich jede Spule wie eine Reihenschaltung aus Wirk- und Blindwiderstand verhält und jeder Kondensator wie eine Parallelschaltung aus beidem. Erinnern wir uns, daß bei sinusförmigen elektrischen Größen an idealen Spulen die Spannung dem Strom und 90° (/2) vorauseilt, während es an idealen Kondensatoren der Strom ist, der um diesen Phasenverschiebungswinkel der Spannung vorauseilt. In der technischen Wirklichkeit variiert die Kombination aus Wirk- und Blindwiderstand in einer Breite, die von der Vernachlässigung der Wirkwiderstände bis zu ihrer gewollten Kombination reicht. Das ändert aber nichts an der mathematischen Modellierung des Verhaltens der Bauelemente in ihren verschiedenen Kombinationen. Im folgenden werden einige prinzipielle Möglichkeiten hierfür zusammengetragen. Dabei beschränken wir uns auf die für diesen Kurs unverzichtbaren Varianten und Darstellungen. Das Verständnis der folgenden Zusammenhänge ist die Voraussetzung dafür, die Vorgänge in elektrischen Maschinen zu begreifen. Das ist ein Schwerpunkt in diesem Kurs. Darüber hinaus lernen Sie am Beispiel technisch relevanter Systeme die Anwendung von Modellen im pädagogischen Erkenntnisprozeß am eigenen Leibe kennen und hoffentlich auch schätzen. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 18 Reihenschaltung 3 Varianten der Reihenschaltung Erklärung I UR UL UR I Uges UC I Uges UC UL UR Uges Nach der Maschenregel sollte gelten: U ges I R I X L U ges I R I X C Die Stromstärke ist bei Reihenschaltungen gleich! Uges UL UR U ges I R ( I X L I X C ) I UC UR UL Uges UC Uge I ? UR I s 2 U ges U R2 U XL U ges I R 2 X L 2 2 U ges U R2 U XC U ges U R2 (U XL U XC ) 2 U ges I R 2 X c2 U ges I R 2 ( X L X C ) 2 Gesamtspannung und Stromstärke der Schaltung bilden den Scheinwiderstand Z. U ges I Z R XL 2 2 U ges I Z R X WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 2 2 c U ges I Z R2 ( X L X C )2 19 Die hergeleiteten Beziehungen bringen zum Ausdruck, daß sich bei Reihenschaltung von Wechselstromwiderständen die Spannungen ebenso verhalten wie die Widerstände. Die folgenden Zeigerdiagramme verdeutlichen das. I Uges Ul UR I UR UC UC Uges UL Uges I UR Z XL R WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik Z R XC XC XL Z R 20 Parallel- und Reihenschaltung der Bauelemente R,L,C im Wechselstromkreis Varianten der Parallelschaltung Iges U Iges R L IR IL I ges I R I L I ges U U R XL Iges U R C U IC IR L IR IL C IC I ges I R I L I c I ges I R I C I ges R U U R XC I ges ? U U U R X L XC Die Spannung ist bei Parallelschaltung gleich! U IR Iges IL Iges I ges I R2 I L2 IR I ges I R2 I C2 WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik U Iges IC IR U IC IL cos IR I ges I ges I R2 ( I L IC )2 21 Aus den Beziehungen der Stromstärken lassen sich die Beziehungen der Widerstände herleiten. I ges I R2 I L2 I ges I R2 ( I L IC )2 I ges I R2 I C2 Der Gesamtwiderstand von „Wechselstromwiderständen“ wird als Scheinwiderstand Z bezeichnet. U U U Z R X L 2 2 U U U Z R X C 2 2 U U U U Z R X L XC 2 2 Durch das Ausklammern der gemeinsamen Größe, der Spannung erhält man die Leitwerte der Widerstandskombinationen: 1 1 1 Z R X L 2 2 1 1 1 Z R X C 2 2 1 1 1 1 Z R X X L C 2 Y Als reziproke Größe des Scheinwiderstandes Z ist der Scheinleitwert Y definiert. Als reziproke Größe des Blindwiderstandes X ist der Blindleitwert B definiert. B Für die Leitwerte ergibt sich: Y G 2 BL2 Y G 2 BC2 2 1 Z 1 X Y G 2 ( BL BC ) 2 Merke: 1. Bei Parallelschaltung von Spulen, Kondensatoren und Widerständen ist die Spannung gleich. 2. Die Stromstärken und die Leitwerte müssen geometrisch addiert werden. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 22 Wechselstromleistung Viele elektrische Maschinen und Geräte werden mit Wechselspannung und -strom angetrieben. Das bedeutet nichts anders, als daß die von ihnen abgegebene Leistung in Form von Wechselstromleistung zugeführt wird. Transformatoren, Elektromotoren und einige Beleuchtungsanlagen verfügen über Wicklungen, die neben ihrem induktiven Blindwiderstand XL auf Grund der Widerstandseigenschaften des Wicklungsmaterials einen beachtlichen Wirkwiderstand R aufweisen, der nicht zu vernachlässigen ist. Der Scheinwiderstand dieser Maschinen, Geräte und Anlagen führt zu Phasenverschiebungen zwischen Strom und Spannung, die nicht ohne nachteilige Folgen für das Elektroenergieversorgungssystem sind. Das ist der Grund dafür, warum wir uns nun mit der Spezifik der Wechselstromleistung befassen müssen. Bei Wechselstrom schwingt die Leistung ebenso wie Stromstärke und Spannung ständig zwischen einem Maximum und einem Minimum. P U max sin t I max sin( t ) P U I Sie folgt der Beziehung: Je nach Art der Verbraucher treten folgende Fälle auf: 1. Die Spannungsquelle wird mit einem Wirkwiderstand R belastet Reiner ohmscher Widerstand 7 Zwischen Strom und Spannung liegt keine Phasenverschiebung vor. 6 5 4 U,I,P 3 2 1 -2 -3 6, 2 5, 8 5 5, 4 4, 6 4, 2 3, 8 3 3, 4 2, 6 2, 2 1, 8 1 1, 4 0, 6 t 0, 2 0 -1 wt Die Leistungskurve ist im positiven Bereich, so daß der Widerstand in jedem Augenblick elektrische Leistung aufnimmt und sie z.B. als Wärme abgibt. -4 WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 23 2. Die Spannungsquelle wird mit gemischtem Widerstand aus R und XL belastet. Das ist der praktische Fall. Im 1. Fall beträgt die Phasenverschiebung 0,125 Pi, das sind etwa 1,26 ms, die die Spannung dem Strom voraus eilt. Phasenverschiebung 0,125 Pi Phasenverschiebung 0,25 Pi 7 6 6 5 5 4 4 3 2 U,I,P 2 1 5, 6 6 6, 4 6 6, 4 4 3, 6 3, 2 2, 8 5, 2 3 3 2 2 1 6, 4 6 5, 6 5, 2 4, 8 4, 4 4 3, 6 3, 2 2, 8 2 2, 4 1, 6 1, 2 0, 8 0, 4 4 3, 6 3, 2 2, 8 2 2, 4 1, 6 1, 2 -1 0, 8 0 0 0 0, 4 U,I,P 1 0 U,I,P 5, 6 4 4 -2 2 Phasenverschiebung 0,5 Pi 5 -1 2, 4 1, 6 1, 2 Phasenverschiebung 0,375 Pi 5, 2 -4 4, 8 -3 -4 4, 8 -2 -3 4, 4 -2 wt 4, 4 wt 0, 8 6 6, 4 5, 6 5, 2 4, 8 4 4, 4 3, 6 3, 2 2, 8 2 2, 4 1, 6 1, 2 0, 8 0, 4 0 -1 0, 4 0 0 -1 1 0 U,I,P 3 wt -2 -3 -3 -4 -4 wt Mit wachsendem Blindanteil wächst die Phasenverschiebung und mit ihr die Blindleistung. Die Leistung unterhalb der Zeitachse ist negativ. Sie heißt Blindleistung Q und hat die entgegen gesetzte Richtung zur Wirkleistung P über der Zeitachse. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 24 Die vorangegangenen 3 Fälle sollen deutlich machen, daß es entsprechend der Belastungsfälle von Spannungsquellen 3 Arten elektrischer Leistung gibt. 1. Der Anteil der Leistung, der vom Widerstand in Arbeit oder Wärme umgesetzt wird heißt Wirkleistung P 2. Der Anteil der Leistung, der zwischen Spannungsquelle und Widerstand hin und her pendelt heißt Blindleistung Q 3. Die nach der Beziehung berechnete Leistung heißt Scheinleistung S. In ihr spielt die zeitliche Verknüpfung von Strom und Spannung keine Rolle. Strom und Spannung sind sinusförmige Wechselgrößen, die Leistung ist es auch, allerdings mit der doppelten Frequenz. Deshalb können auch die Leistungen mit Zeigerdiagrammen dargestellt werden. S Z XL R Q P S U I P S cos U I cos Q S sin U I sin S 1V A 1VA P 1V A 1W Q 1V A 1var Um die Leistungen gegeneinander abzugrenzen wurden ihnen auch unterschiedliche Einheiten zugeordnet. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 25 Deutung von Wirkleistung, Blindleistung und Scheinleistung Scheinleistung Blindleistung Q Die Wirkleistung ist der Anteil der Scheinleistung, der beim Verbraucher Arbeit verrichtet und dabei letztendlich in Wärme übergeht. Die Blindleistung belastet das Netz und beeinträchtigt die effektive Übertragung der Wirkleistung. Um das zu verhindern, gibt es technische Maßnahmen. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 26 Aufgaben 11. Ein unter Umständen schon lebensgefährlicher Strom von 40 mA fließt durch den menschlichen Körper und überwindet dabei einen Widerstand von 1 k. Welche Spannung reicht hierzu aus? (U=40V) 12. In einer Spule ändert sich der magnetische Fluss wie im ,t -Diagramm dargestellt. Berechnen Sie die für die drei Zeitabschnitte I , II, III induzierten Spannungen ui für eine Induktionsspule mit N = 300. Induktionsgesetz anwenden! 13. Der Leistungsfaktor (cos des Phasenverschiebungswinkels) eines Elektromotors von P=1,5 kW Wirkleistung beträgt 0,89. Wie groß ist die Stromstärke bei einer Netzspannung von 230 V? (I = 7,33 A) 14. Ein Elektromotor für die Nennspannung 230 V und mit einer Leistung von 2 kW hat einen Leistungsfaktor von 0,87. Wie groß sind seine Schein- und Blindleistung? Welchen Betrag hat der Phasenverschiebungswinkel und um wie viele Sekunden eilt die Spannung der Stromstärke voraus? (S = 2,3 kVA, Q = 1,13 kvar, = 29,5°; t= 1,63 ms) WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 27 Hier ist der Ausgangspunkt zur Beschreibung des Verhaltens der Schaltung die Maschenregel, die besagt, daß in einem Stromkreis die Summe der Spannungsabfälle gleich der angelegten Spannung ist. Dafür gibt es bei der Reihenschaltung aber nur eine Stromstärke. Wie bereits bekannt ist, sind die Werte induktiver und kapazitiver Blindwiderstände frequenzabhängig und wirken pasenverschiebend, so daß die Dinge dadurch etwas komplizierter sind und die Spannungsabfälle nicht einfach arithmetisch wie im Gleichstromkreis addiert werden können. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 28 Eine von Wechselstrom durchflossene Spule mit der Induktivität L wirkt ebenfalls als Blindwiderstand und wird als induktiver Blindwiderstand bezeichnet. Um die Strom - Spannungsverhältnisse der Spule zu klären, bedarf es folgender Modellvorstellungen. Zunächst geht man davon aus, das die Spule keinen Wirkwiderstand hat. D.h., der Widerstand des Leitermaterials der Spule ist 0. Weiterhin wissen wir, daß in einem Stromkreis die Summe der Spannungsabfälle gleich groß der Summe der Spannungen ist. Die Summe der Spannungsabfälle in einem widerstandslosen Stromkreis ist wegen der fehlenden Wirkwiderstände 0. Folglich ist auch die Summe der Spannungen 0. Das gilt für die Spannung der Spannungsquelle und die Selbstinduktionsspannung der Spule. Für diesen Modellfall gilt somit: WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 29 Prinzip des Wechselstromgenerators Leiterschleife rotiert im Magnetfeld. Nacheinander wird auf einer Kreisbahn jeder Leiterzug am Nord- und am Südpol vorbeigeführt. Es entsteht eine elektrische Spannung, deren Verlauf sinusförmig ist und deren Polarität sich periodisch ändert. Bei Anschluss eines Verbrauchers an die Schleifringe fliesst ein sich periodisch ändernder sinusförmiger Wechselstrom. Darstellung und Berechnung von sinusförmigen Wechselspannungen und strömen Im Sinne einer Leiterschleife dreht sich ein Zeiger umax , dessen Sinus je nach Drehwinkel eine entsprechende Projektion u im Liniendiagramm erzeugt. Im 1. und 2. Quadranten des Koordinatensystems ist die Amplitude der Schwingung positiv, im 3. und 4. Quadranten ist sie negativ. Entsprechen verläuft eine induzierte elektrische Spannung u. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 30 Der Widerstand R hat die Funktion, den folgenden Vorgang verlangsamt ablaufen zu lassen. Im Prinzip könnte er entfallen. Der Vorgang ist dann beendet, wenn U und u(t) den gleichen Betrag haben, sich die Spannung am Kondensator also nicht mehr ändern kann. Die vom Kondensator aufgenommene Energie wird in Form des elektrischen Feldes gespeichert. Im Unterschied zur Spule kann ein Kondensator Energie über einen längeren Zeitraum speichern. Nach Betätigung des Schalters liegt vor dem Widerstand R sprunghaft die Spannung U der Spannungsquelle an und treibt durch den Widerstand R einen Ladestrom in den Kondensator. Unmittelbar nach dem Einschalten ist die Ladespannung des Kondensators 0. Der Strom, der in diesem Moment fließt hat einen Maximalwert, der lediglich durch R begrenzt wird. Mit fortschreitendem Vorgang lädt sich der Kondensator auf, wobei er seine Ladespannung erhöht. Infolge der sich erhöhenden Ladespannung verringert sich die Differenz zwischen der Spannung U und der Ladespannung u(t). Die Folge ist die Abnahme des Ladestromes i(t). Für den Ladevorgang gilt die Beziehung: dU i C dt Der Vorgang ist dann beendet, wenn U und u(t) den gleichen Betrag haben, sich die Spannung am Kondensator also nicht mehr ändern kann. Die vom Kondensator aufgenommene Energie wird in Form des elektrischen Feldes gespeichert. Im Unterschied zur Spule kann ein Kondensator Energie über einen längeren Zeitraum speichern. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 31 Nach Betätigung des Schalters liegt an der Spule die Spannung u sprunghaft an. Durch einen Ohmschen Widerstand würde ein ebenso sprunghafter Strom i fließen. Anders bei der Spule, deren wesentliche Eigenschaft ihre Induktivität L = N2/Rm ist. Infolge der Induktivität und auf der Grundlage des Induktionsgesetzes entsteht in der Spule selbst die Induktionsspannung u0 . Die Induktionsspannung ist aber ihrem ursächlichen Strom, der in ihr den sich verändernden magnetischen Fluß verursacht, entgegengerichtet (LENZsche Regel). Die Folge ist, daß sie dem Strom entgegenwirkt, etwa wie ein Widerstand. Der Strom steigt deshalb verzögert an, wobei der Stromanstieg mit fortschreitender Zeit immer geringer wird. Erst wenn die Stromstärke einen konstanten Wert erreicht hat, ändert sich das Magnetfeld der Spule nicht mehr, so daß auch keine Induktionsspannung mehr entstehen kann. Wird der Schalter geöffnet und der nunmehr konstante Strom durch die Spule wird sprunghaft verringert, so geht das wiederum nur mit einer Änderung des magnetischen Flusses einher. In diesem Fall verlaufen alle Wirkungen genau entgegengesetzt. Der zusammenbrechende magnetische Fluß induziert eine Spannung, deren Richtung dem Abschalten entgegenwirkt, also die Induktionsspannung die Stromstärke aufrechterhält. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 32 Der Widerstand R hat die Funktion, den folgenden Vorgang verlangsamt ablaufen zu lassen. Im Prinzip könnte er entfallen. Nach Betätigung des Schalters liegt vor dem Widerstand R sprunghaft die Spannung U der Spannungsquelle an und treibt durch den Widerstand R einen Ladestrom in den Kondensator. Unmittelbar nach dem Einschalten ist die Ladespannung des Kondensators 0. Der Strom, der in diesem Moment fließt hat einen Maximalwert, der lediglich durch R begrenzt wird. Mit fortschreitendem Vorgang lädt sich der Kondensator auf, wobei er seine Ladespannung erhöht. Infolge der sich erhöhenden Ladespannung verringert sich die Differenz zwischen der Spannung U und der Ladespannung u(t). Die Folge ist die Abnahme des Ladestromes i(t). Für den Ladevorgang gilt die Beziehung: i C dU dt Der Vorgang ist dann beendet, wenn U und u(t) den gleichen Betrag haben, sich die Spannung am Kondensator also nicht mehr ändern kann. Die vom Kondensator aufgenommene Energie wird in Form des elektrischen Feldes gespeichert. Im Unterschied zur Spule kann ein Kondensator Energie über einen längeren Zeitraum speichern. Hinsichtlich des zeitlichen Verhaltens von Strom und Spannung liegen am Kondensator die Verhältnisse in genau umgekehrter Weise im Vergleich zur Spule vor. Unmittelbar nach dem Einschaltmoment ist die Spannung am Kondensator am kleinsten, der in ihn hineinfließende Strom dagegen am größten. Man sagt, „der Strom eilt der Spannung voraus“ oder „die Spannung eilt dem Strom nach“. WWU – Institut für Technik und ihre Didaktik – Hein Elektronik/Elektrotechnik – 3.1Grundlagen der Wechselstromtechnik 33