1b. Quantenphysik

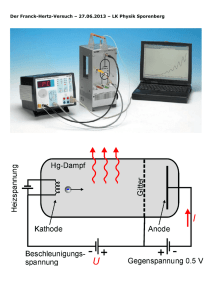
Quantenphysik in Lebens- (und)
medizinischen) Wissenschaften
Erscheinungen und Experimente die über die
klassischen (Newton’schen) Physik zeigen
Péter Maróti
Professor für Biophysik, Universität von Szeged, Ungarn.
Lehrbücher:
Biophysik für Mediziner (Herausgeber S. Damjanovich, J. Fidy und J. Szöllősi) Medicina, Budapest, 2008.
Fercher A.F. Medizinische Physik, Springer, Wien, New York 1992.
Haas U. Physik für Pharmazeuten und Mediziner; Wissenschaftliche Verlagsgesellschaft mbH. Suttgart 2002.
Maróti P., Laczkó G.: Bevezetés a biofizikába, JATEPress, Szeged 1998 (Ungarisch)
P. Maróti, L. Berkes, F. Tölgyesi: Biophysics Problems. A Textbook with Answers. Akadémiai Kiadó, Budapest 1998
(Englisch).
Kritische Experimente die zur Ausbildung
der Quantenphysik führten
I. Temperaturstrahlung und die UV Katastrophe
Experimentelle Verwirklichung des absoluten schwarzen Körpers
Ein ganz
kleines Loch
Im Körper mit schwarzen
Wänden entsteht
Gleichgewicht zwischen
Absorption und Emission der
Strahlung.
Das Loch an dem Reservoir
verwirklicht die Bedingungen
Strahlung
des (absolut) schwarzen
Körpers, weil die Strahlung,
die von außen eintritt, praktisch
Die Wand des Körpers (nach zahlereichen Reflexionen
an den schwarzen Wänden) nie
gehalten bei
austreten wird.
Temperatur T
Temperaturstrahlung
Das Spektrum (die
Strahlungsdichte gegen der
Wellenlänge) des absoluten
schwarzen Strahlers bei
verschiedenen
Temperaturen gemesst in
absoluten Werten (K).
ρ ist die Energiedichte
der Strahlung E (J/m3)
durch die Einheit der
Wellenlänge Δλ (m):
Sichtbares Bereich
des Spektrums
ρ = E/ Δλ
Die vier Strahlungsgesetze der klassischen Physik aufgestellt am Ende des 19.
Jahrhunderts (vor der Quantenphysik):
1. Kirchhoff’sches Gesetz: e/a = E(λ,T),
ρ (λ)
es ist gültig für alle Körper (also nicht nur
für absoluten schwarzen Körper).
e: Ausstrahlung (Emission) und
a: Absorptionsgrad des Körpers.
Für absoluten schwarzen Körper a = 1.
2. Wien’sches Verschiebungsgesetz:
T·λmax= 2896 μm·K (Konstante)
T: absolute Temperatur und
λmax: die Wellenlänge der
Temperaturstrahlung wo ρ maximal ist.
3. Stefan-Boltzmann-Strahlungsgesetz:
Etotal = σ·T4
λ (nm)
Die erste drei Gesetze sind gültig, aber
Etotal : Gesamtenergie ausgestrahlt per
Flächeneinheit und
σ = 56,7 nW·m-2·K-4.
4. Rayleigh-Jeans-Gesetz:

das Rayleigh-Jeans-Gesetz führt zur Katastrophe im UV Spektralbereich.
8 k T
4
Versuche zur (theoretischen) Beschreibung des
Spektrums der Temperaturstrahlung
1. Die Ultraviolettkatastrophe
Strahlungsdichte,
Die Rayleigh-Jeans Kurve:

Strahlung des
schwarzen
Körpers:
Experiments
Wellenlänge,
8 k T
4
Annahme der klassischen Physik: der
lineare Oszillator im strahlenden
schwarzen Körper kann alle Größe der
Anregungsenergie aufnehmen (und auch
abgegen): die Energie kann also beliebig
klein (oder groß) sein. Diese Annahme
führt aber zur Ultraviolettkatastrophe.
2. Das Planck’sche Strahlungsgesetz
Strahlungsdichte,
Die Planck’sche Funktion
8 hc 
1

 4
 hc / kT

  e
1
Die Annahme von Planck: die Energie des
Strahlung des elektromagnetischen Oscillators kann sich
schwarzen
nicht kontinuierlich ändern. Der Oscillator
Körpers:
kann nur sehr bestimmte Energiewerte
Experiments
(Quanten) aufnehmen (abgegen):
E = n·hν,
wo n = 0, 1, 2, …, ist eine natürliche Zahl,
Frequenz der Strahlung und
Schlußfolgerung: die Energie des ν (= c/λ) ist die
h = 6,626·10-34 J·s ist die sogenannte
elektromagnetischen Oscillators is Planck’sche Größe (Zahl, Konstante).
Wellenlänge,
gequantelt.
II. Temperatur-Abhängigkeit der spezifischen
Wärme des Festkörpers
Die Dulong-Petit Regel: die spezifische (molare) Wärme ist eine Konstante, hängt nicht
von der Temperatur (und der Materie) ab.
 U m 
CV, m  
  3 R
 T V
Mit der Annahme der klassischen
Physik: die Energie verteilt sich
gleichmäßig unter den Teilchen
(Oszillatoren) des Festkörpers. Das ist
das Prinzip der Equipartition.
Aber: Abweichungen vom konstanten
Wert wurden beobachtet bei niedrigen
Temperaturen.
warm
kalt
Die Annahmen der Quantenphysik:
die Oszillatoren bewegen sich mit
einzelner und identischer Frequenz
(Einstein) oder mit einer Verteilung
der Frequenzen (Debye).
Temperatur-Abhängigkeit der spezifischen Wärme des
Festkörpers
Einstein berechnete die molare spezifische
Wärme mit der Annahme, daß (nach der
Hypothese von Max Planck) die Energiewerte
der atomaren Oszillatoren (Schwingungen)
gequantelt sind:
 h 
Typisches Experiment
 2kT 
h

 e

C  3R f 2 , wo f 
kT  h 1 
 e kT 


Der Ausdruck führt die Temperaturabhängig
der spezifischen Wärme ein.
Eine bessere Beschreibung hat P. Debye mit der
Annahme einer Verteilung von verschieden
Frequenzen erhalten.
Sclußfolgerung: nicht nur die Energie
des elektromagnetischen Feldes,
sondern auch die Energie der
atomaren Oszillatoren ist gequantelt.
Θ: karakteristische Temperatur
III. Gequantelte Energieänderungen in Atomen
Aufnahme der
Spekrallinien
der Emission
des
Hidrogenatoms
Spektrale
Verteilung der
Strahlungslinien
einiger Gase
Mögliche Energiezustände des Hidrogenatoms
sichtbar
Balmer-Reihe:
Balmer sorozat:
Kopflinie
Reihe
Kopflinie
Kopflinie
Bindungsenergie
Reihe
Reihe
nah infrarot
fern infrarot
Wellenlänge
Empirische Beschreibung der Spektrallinien
des Hidrogenatoms
Beobachtungen von Balmer: die Frequenzen der Familie der Spektrallinien der
Strahlung im sichtbaren und im nahen infraroten Bereich lassen sich mit einem
einfachen empirischen Ausdruck beschreiben:
 1
  R H  
 22

1 

2
n 
wo RH = 3,29·1015 s-1 ist die Rydberg Konstante des Hidrogenatoms und n = 3, 4, 5,…
Später, auch weitere Linienfamilien wurden in den ultravioletten und infraroten
Spektralbereichen entdeckt, die man mit ähnlichen empirischen Ausdrücken
beschreiben konnte:


1
1 

  RH  2  2
n

 L nH 
Hier nL und nH sind beliebige ganze Zahle. Die kleinere Zahl karakterisiert die
Familiensorte (Lyman, Balmer, Paschen, Pfund,...) und die größere Zahl die
Spektrallinie in der Famile.
Photoelektrischer (Hallwachs) Effekt
Anode
Kathode
Die verschiedene
lichtempfindliche
Photokathoden haben
verschiedenen
Grenzwellenlängen (siehe die
Zahle im Klammern). Über
dieser Wellenlänge, das
Anregungslicht kann kein
Photoelektron auslösen.
Licht
Elektrische
Stromstärke
(rel. Einheit)
Photoelektrischer (Hallwachs) Effekt
Energie
Photoelektron
Freies
Elektron
Kinetische
Energy des
Photoelektrons
Schwelle
der
Frequenz
Kein Photoelektron
1
  me v 2  h 
2
Kinetische Energie des
befreiten Elektrons
Photoelektrische Gleichung von Einstein
Frequenz, ν
Energie (Austrittsarbeit)
zur Befreiung des
gebundenen Elektrons im
Metal.
Gebundenes Elektron
Grundgesetze des photoelektrischen
Effekts
1) Bedingung des photoelektrischen Effekts: die Energie des Photons muß größer sein
als die Austrittsarbeit des Elektrons vom Metal.
h   
Die Schwellefrequenz des Anregungslichtes ist durch die Austrittsarbeit des Elektrons
bestimmt.
2) Die kinetische Energie des Photoelektrons hängt von der Farbe (Frequenz) des
Lichtes ab und ist unabhängig von der Intensität des Lichtes.
1
me v 2  h   
2
3) Die Intensität des Lichtes bestimmt die Zahl des Photoelektrons.
4) Die Absorption des Anregungslichtes und der Austritt des Photoelektrons sind
(praktisch) gleichzeitige Ereignisse. Es ist also nicht erlaubt die Zugabe der
akkumulierten Energie von mehreren absorbierten Photonen zu einem Elektron.
Franck-Hertz Experiment
Das sollte eine der schönsten und elegantesten Experimente zum Beweis der
gequantelten Natur der Energiezustände des Atoms.
Kathode
UV Licht
Gitter 1
Anode
Gitter 1
Die Wellenlänge des emittierten Lichtes ist

hc
e U
Bei der ersten Stufe U = 4,9 V, d.h. λ = 253,7 nm
Weil das Elektron bei der bestimmten
Spannungen (die den Stufen
entsprechen) mit den Hg Atomen
unelastisch anstoßt (die
Geschwindigkeit des Elektrons
verschwindet sich vollständig), die
Sprünge in der I - U Charakteristik
reflektieren die möglichen (diskreten)
Energiewerte des Hg Atoms.
IV. Dualität der Teilchen; Teilchen als Wellen
Diffraktion der
Röntgen Strahlen
Elektronen
Davisson-Germer
Experiment
Die Elektronen
wurden auf eine
dünne Metalplatte
gerichtet und die
durchgehende
Elektronen
wurden auf einer
photographischen
Schicht detektiert.
Ein sehr definiertes Diffraktionsbild wurde erhalten wenn die Elektronen zur hochen
Geschwindigkeit (zu welchem Wert eine de Broglie-Wellenlänge von 0,50 Å gehört) beschleunigt
wurden. Das Diffraktionsbild ist ähnlich zum Diffraktionsbild welches man bei Röntgenstrahlen
(Wellenlänge von 0,71 Å) bekommt.
Die Gleichung nach de Broglie
Der Zusammenhang zwischen den Teilchen- und Welleneigenschaften kommt von dem
allgemeinen Ausdruck zwischen Masse und Energie von Einstein:
E = mc2.
Nach dem Planck’schen Gesetz:
E = h = hc/.
Wir können die Definition des Impulses der elektromagnetischen Welle
p = mc
mit der Energie zusammenbinden: p = E/c, oder p = h/λ.
Nach einfachem Umordnen

h
h

p mv
Anwendung zur Bestimmung der Auflösungsgrenze verschiedener Mikroskope:
Nach Abbe, δ = 0.61·λ/(n·sinα), wo NA = n·sinα ist die numerische Apertur.
Elektronenmikroskop: wenn v = c/50, (c ist die Lichtgeschwindigkeit), δ ~ λ = 0,12 nm.
Hypothetisches Neutronenmikroskop: weil mNeutron ≈ 2000·mElektron,
δNeutron ~ λNeutron ≈ λElektron / 2000 ~ δElektron /2000
V. Der quantenmechanische Tunneleffekt
Damm
Zwei Möglichkeiten der Transmission:
1) Thermische Aktivation (Arrhenius) und
Das Teilchen nähert sich
zum Potentialdamm
Δx
T
1.0
2) Tunneleffekt (Gamow)
Energie
ΔE
k = k0·exp(-ΔE/kBT)
ΔE
und kann mit
niedriger
Wahrscheinlichkeit
durchgehen.
Gamow’scher Ausdruck für Transmission


2
8

m


T  exp   2

E


x


h2


Koordinaten
Die Temperaturabhängigkeit der zwei Prozesse
sind verschieden: die Rate der Transmission
1) hängt stark von der Temperatur ab (Arrhenius),
2) ist unabhängig von der Temperatur (Gamow).
Berechnung der Wahrscheinlichkeit der
Transmission durch Tunnel Effekt
Was ist die Wahrscheinlichkeit, daß ein Proton bzw. ein Deuterium von 0,9 eV Energie
durch einen Potentialdamm der Höhe von 1,0 eV und Breite von 100 pm passieren
kann?
Die Masse des Protons ist m = 1,673·10-27 kg, die Planck’sche Konstante ist
h = 6.626·10-34 J·s, die Differenz der Höhe des Dammes und der Energie des Teilchens
sind ΔE = 0,1 eV (diese Höhe sollte mit Tunnel Effekt besiegt werden), und die Breite
des Dammes beträgt Δx = 100 pm.
Benutzen wir den Gamow’schen Ausdruck:


8 2m


T  exp   2

E


x


h2


Folgerungen: 1) die Wahrscheinlichkeit der Transmission via Tunnel Effekt für Proton ist
Tp = 9,56·10-7, was ungefähr 300-mal größer ist als für Deuterium: Td = 3,07·10-9.
2) Dieses Verhältnis wird viel größer sein, wenn der Damm zweimal breiter wird (unter
gleichen anderen Bedingungen): Tp/Td = 9·104.
Der Isotop Effekt ist besonders groß bei Hidrogen and Deuterium, deswegen man kann
die protolytische Reaktionen mit diesem Method erfolgreich studieren.
Quantum Tunnel Effekt: Tunnelmikroskop
(Scanning Tunneling Microscope, STM)
Wenn die Entfernung (d) sehr klein ist, das Elektron springt von einer Elektrode (Taster)
auf die andere Elektrode (Oberfläche) mit Hilfe des Tunnel Effekts.
Wenn der Taster sich mit der Oberfläche parallel bewegt, die gemessene Stromstärke (I)
gibt Hinweis auf den Abstand zwischen den Elektroden. Auf diese Weise, wir können
aus der Änderungen der Stromstärke auf die Unregelmäßigkeiten der Fläche folgern.
Licht
Rate des Transfers von Elektronen
Transfer von Elektronen durch Tunnel Effekt in
Reaktionszentrum Protein der photosynthetischen Bakteria
k
Tunnel Effekt
(z.B. P→BA→HA)
Thermische Reaktionen
(z.B. QA→QB)
1/T
Hohe
Temperatur
Niedrige
Temperatur
Die fasteste Anfangsreaktionen des Transfers
von Elektron nach Lichtanregung sind nicht
thermische sondern Tunnel Reaktionen.
Die Lage der Kofaktore, Elektron Transfer Routen (Pfeile) und die entsprechende Zeitkonstante in Rb.
sphaeroides. P: Bakterioklorofill (BChl) Dimer, B: monomerisches BChl, H: Bakteriofeofitin, Q: Quinon, Fe: Eisen
Atom, A: photoaktiver Zweig, B: photoinaktiver Zweig. In der Mitte der Klorin, Kreis zeigt die Lage des Mg Atoms in
BChl.
VI. Spin und die magnetische Flußdichte (Induktion)
Experiment von Einstein und de Haas
N : mechanisches Momentum (Drehmoment)
M : Magnetisierung der Eisenstange (Barren)
Wir suchen Zusammenhang zwischen der
Torsionsbewegung und der Magnetisierung des
Barrens. Nehmen wir an, daß n Elektronen je mit j
Momentum existieren und zur Magnetisierung der
Stange beitragen.
 q 
M

n

M

ng

 j
Barren
Elektron
q =-e: elementare elektrische
 2mc 
Ladung des Elektrons,
Weil n  j  N  0 deswegen
c: Lichtgeschwindigkeit,
 q 
 e 
 
μB: Bohr Magneton
M Barren   g 
  N   g
  N   g B   N
 2mc 
 2mc 
  
Mit der Messung der makroskopischen Größen N und MBarren, wir können das
giromagnetische Verhältnis, den Lande Faktor g bestimmen: g = 2.
m: die Masse des Elektrons,
Dieses Ergebnis sagt, daß die ferromagnetische Eigenschaft des Eisenbarrens kann
nicht ausschließlich von dem Bahnmoment des Elektrons kommen, sondern das
Elektron noch dazu ein eigenes und spezielles magnetisches Momentum, das SPIN
haben müsste.
Abweichung von Silver (Ag) Bündel im
inhomogenen magnetischen Feld:
Das Stern-Gerlach Experiment
Klassische Physik:
die Abweichung nach dem
Winkel muß kontinuierlich
sein.
Spaltung der D Spektrallinie von
Sodium (Na) im magnetischen Feld:
Der Zeeman Effekt.
Kein magnetisches Feld,
keine Spaltung
N
S
Quantenphysik:
Wir müssen nur zwei,
gut getrennte Bündel
bekommen.
Das Experiment zeigte: das Atombündel spaltet
sich auf zwei Bündel im inhomogenen
magnetischen Feld. Folgerungen:
1) Beweis für Quanteneigenschaften nach
Richtung (die physikalische Größ ist
gequantelt nach der Orientierung) und
2) Das magnetische Momentum der Atome
kann man direkt messen.
Magnetisches Feld,
Spaltung der Linien
Der Energiezustand des Elektrons wird
auf mehreren und nahe liegenden
Zustände im magnetischen Feld
aufgespaltet. Der Effekt ist genannt als
Zeeman-Spaltung.
Pauli Prinzip zum Aufbau der Elektronhülle
Elektronkonfigurationen der ersten 18 Elemente der Periodentafel im Grundzustand
Aufbau Prinzip der Elektronhülle
Bahn
Spin (S) – Bahn (L)
Kopplung
groß
Gesamt
Parallele
Richtung der
zwei
Komponente
Spin
klein
Antiparallele
Richtung der
zwei
Komponente
Nicht nur die Elektronen sondern auch andere Teilchen und
Atomkerne haben eigenes magnetisches Moment (Spin).
Magnetische Eigenschaften einiger Atomkerne die biologisch wichtig sind.
Das giromagnetische Verhältnis γ bestimmt die Energie
der elektromagnetischen Strahlung, die das Spin des
Atomkerns nach Absorption der Strahlung umkippen
kann. Die Energie des Quantums der Strahlung ist gleich
der Energiübergang des Atomkerns. Sie sind in Resonanz.
Frequenz der Resonanz
(bei 4,7 T magnetischer
Flußdichte)
Giromagnetisches Verhältnis
Kernspin Quantenzahl
Vorkommen in der Natur
Hausaufgaben
1. Wie groß ist etwa die Auflösungsgrenze des Elektronenmikroskops wo die
Elektronen zum 1% der Lichtgeschwindigkeit beschleunigt sind?
2. Wieviele Photonen emittiert das Nachtglas (1000 nm Wellenlänge und 1 mW
Leistung) innerhalb 0,1 s?
3. Zeichnen Sie den Verlauf der Strom-Spannung Charakteristik im FranckHertz Experiment auf, wenn die intensivsten Linien des Quecksilberdampfes
befinden sich bei den folgenden Wellenlängen (in nm):
184,45, 253,7, 300,0, 312,1 334,0, 365,4, 404,7, 435,8, 546,1 und
579,1.
Hausaufgaben
4. Berechnen Sie die Wellenlänge des Elektrons nach dem Verlassen den
Beschleuniger von 10 MeV!
5a. Wie groß ist etwa die Temperatur der Oberfläche der Sonne wenn die Wellenlänge
des Maximums der Strahlung fällt mit dem Maximum der Empfindlichkeit der Auge
zusammen?
5b. Wie groß ist etwa die Temperatur der Oberfläche des Sterns Sirius wenn die
intensivste Strahlung fällt auf Wellenlänge von 263,27 nm?
6. Ein Wurm der Masse 5,0 gramm bewegt sich nach dem Prinzip der Rakete. Er
emittiert rotes Licht (650 nm) mit 0,1 W Leistung. Zu welcher Geschwindigkeit
beschleunigt der Wurm nach 10 Jahren im freien Raum unter permanenten
Bedingungen?
7. In einem Röntgen-Photoelektron Experiment, die Röntgen Strahlung mit
150 nm Wellenlänge befreit ein Elektron von der inneren Hülle des Atoms. Das
Photoelektron besitzt eine Geschwindigkeit von 2,14·107 m/s. Wie groß ist etwa die
Bindungsenergie des Elektrons?