Verteilungen

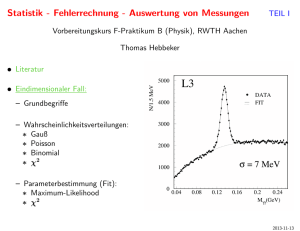
Data Mining
8.5.2007
Georg Pölzlbauer
Datenmatrix (1)
• Messungen werden in Tabellenform
dargestellt
• N Zeilen sind gemessene Objekte xi
(samples, patterns)
• D Spalten sind Merkmale (features,
variables)
 x11  x1D 


X   

x
xND 
 N1
Datenmatrix (2)
• Beispiel: Umfrage; es werden 100
Personen zu ihrer Einstellung zu 5
politischen Parteien gefragt (Bewertung
auf Skala von 0 bis 10)
100 Zeilen, 5 Spalten
• Es gibt auch andere Arten von Daten (z.B.
Zeitreihen, strukturierte Daten, …), diese
sind aber nicht Thema dieser Vorlesung
Geometrische Interpretation (1)
• Samples xi sind Punkte in einem
Vektorraum
• "Datenpunkte" bilden Datenwolke
Geometrische Interpretation (2)
Gewicht
(kg)
100
90
80
70
60
50
40
1,50
1,60
1,70
1,80
1,90 Größe
(m)
Skalentypen (1)
• Nominalskala
Werte stehen in keiner Ordnung zueinander,
unterschiedliche Werte sind sich alle gleich
unähnlich
z.B. Haarfarbe (blond, brünett, schwarz, …)
• Ordinalskala
numerische Skala, aber Abstände zwischen den
Werten haben keine Bedeutung
z.B. Noten (ist der Abstand zw. 4 und 5 genau
so groß wie der zwischen 2 und 3?)
Skalentypen (2)
• Intervallskala
Abstand zwischen 2 Werten kann gemessen
und mit anderen Abständen verglichen
werden
z.B. Temperatur (in Celsius, Fahrenheit)
• Verhältnisskala
wie Intervallskala, man kann aber Verhältnisse
berechnen, hat sinnvollen Nullpunkt
z.B. Gewicht, Größe (Person A ist 1,2x so groß
wie B)
Metriken (1)
• Welche Datenpunkte sind ähnlich?
• Euklidische Distanz (L2-Metrik)
d ( x1 , x2 )  x1  x2 
D
2
(
x

x
)
 1i 2i
i 1
• Manhattan Distanz (L1-Metrik, City-Block)
D
d ( x1 , x2 )  x1  x2   x1i  x2i
i 1
Metriken (2)
Abstand?
Metriken (2)
Euklidische
Distanz
Metriken (2)
City Block
Mittelwert, Varianz (1)
• Arithmetisches Mittel (Mittelwert, mean)
kann pro Merkmal gebildet werden
1
xj 
N
N
x
i 1
ij
• Streuungsmaße wie Varianz bzw.
Standardabweichung können ebenfalls für
jedes Merkmal berechnet werden
Mittelwert, Varianz (2)
Gewicht
(kg)
100
90
80
x2
70
60
50
x1
40
1,50
1,60
1,70
1,80
1,90 Größe
(m)
Mittelwert, Varianz (2)
Gewicht
(kg)
100
90
s2
80
70
60
50
s1
40
1,50
1,60
1,70
1,80
1,90 Größe
(m)
1-zu-N Kodierung (1)
• Die meisten Data Mining Algorithmen
benötigen intervallskalierte Daten
• Problem v.a. bei kategorischen Daten
(nominalskaliert)
• Lösung: Eine binäre Variable für jede
mögliche Ausprägung
1-zu-N Kodierung (2)
feature
red
blue
green
red
red
green
blue
red
1
0
0
1
1
0
0
blue green
0
0
1
0
0
1
0
0
0
0
0
1
1
0
Fehlende Werte
• Oft vorkommendes Problem bei Data
Mining
• Mögliche Lösungen:
– Verfahren verwenden, die damit umgehen
können (Decision Trees, SOMs)
– Diese Samples weglassen
– Werte interpolieren (missing value prediction)
Ausreißer
• Ausreißer können Fehlmessungen oder
einfach stark untypische Samples sein
• Problem bei Berechnung von Varianz,
Kovarianz etc.
• Robuste Statistik: Median, Quartile, etc.
Normalisierung von Daten (1)
Gewicht
(kg)
Abstand = sqrt(0,3^2 + 45^2)
100
= sqrt(2025,09)
90
= 45
80
70
45
60
50
0,3
40
1,50
1,60
1,70
1,80
1,90 Größe
(m)
Normalisierung von Daten (1)
Gewicht
(kg)
Abstand = sqrt(300^2 + 45^2)
100
= sqrt(92025)
90
= 303
80
70
45
60
50
300
40
1500
1600
1700
1800
1900 Größe
(mm)
Normalisierung von Daten (2)
• Die Abstandsmeßung sollte von der
Maßeinheit der Merkmale unabhängig
gemacht werden
• Standardisierung (zero-mean-unitvariance):
zij 
xij  x j
sj
Normalisierung von Daten (3)
Gewicht
(kg)
100
90
80
70
60
50
40
1,50
1,60
1,70
1,80
1,90 Größe
(m)
Normalisierung von Daten (3)
Gewicht
3
2
1
0
-1
-2
-3
5,5
4,5
-2
-1
0
1
2
Größe
Normalisierung von Daten (4)
Chebyshevs Ungleichung
75% der standardisierten Werte zwischen -2
und +2
89% der Werte zwischen -3 und +3
94% der Werte zwischen -4 und +4
Dichtefunktion
• Es wird angenommen, daß den
gemessenen Werten (Datenmatrix) eine
Dichtefunktion zu Grunde liegt
• Diese Funktion ist unbekannt, es ist eine
unserer Aufgaben sie zu schätzen
Normalverteilung (1)
• Die Normalverteilung nimmt in der Statistik
eine besondere Rolle ein
1
f ( x) 
e
 2
1 x 2
 (
)
2 
• Eine Zufallsvariable X ist normalverteilt:
X ~ N ( , )
2
Normalverteilung (2)
Multivariate Verteilungen (1)
• MV Zufallsvariable werden durch
mehrdimensionale Dichtefunktionen
beschrieben
• Für MV Normalverteilung schreibt man
z.B. X ~ N (  , )
Zufallsvektor
Vektor von
Mittelwerten
Kovarianzmatrix
Multivariate Verteilungen (2)
Stichproben (1)
• Die konkreten Ausprägungen, die
gemessen werden, sind Stichproben der
Population
• Die Stichprobe besteht aus N Samples,
Population wird durch kontinuierliche
Dichtefunktion beschrieben
Stichproben (2)
Population vs. Stichprobe
Stichprobe
Mittelwert
Varianz
Population
Bayes Theorem (1)
• Oft stehen Zufallsereignisse mit einander
in Verbindung
• Wenn man z.B. die Ereignisse „die Erde
ist naß“ (A) und „es regnet“ (B) betrachtet:
– Wahrscheinlichkeiten P(A) = 0,15 und P(B) =
0,12
– Mit der Information, daß der Boden naß ist
(also A eingetreten ist), scheint es
wahrscheinlicher, daß es regnet
Bayes Theorem (2)
• Bedingte Wahrscheinlichkeit:
P(B|A) = 0,8
D.h. unter der Voraussetzung, dass der Boden
naß ist, regnet es mit W. von 80% (ohne
dieser Information: 12%)
• Das Bayes Theorem erlaubt die
Berechnung der W. in die andere Richtung
(d.h. wenn man die Bedingung vertauscht)
Bayes Theorem (3)
• Bayes Theorem:
P( A)  P( B | A)
P( A | B)
P( B)
• Z.B.: P(A|B)… W. daß der Boden naß ist wenn
es regnet
• P(A|B) = 0,15*0,8/0,12 = 1
Kovarianz
• Kovarianz mißt die Stärke des linearen
Zusammenhangs zweier Variablen
Gewicht
(kg)
100
90
80
70
60
50
40
1,50 1,60 1,70 1,80 1,90
Größe
(m)
Kovarianzmatrix
• Die Kovarianzmatrix hat die Varianzen der
Variablen in der Diagonale, und die
Kovarianzen außerhalb der Diagonale
• Beispiele:
2
  1  12  13 
2


  1  12 
2

  






12
2
23 
2 

2 
 12  2 
 13  23  3 
Korrelation
• Standardisierte Kovarianz (dimensionslos,
zwischen -1 und +1, ähnlich
Normalisierung)
• Negative Korrelation: Wenn x1 steigt, sinkt
x2
• Positive Korrelation: Wenn x1 steigt, steigt
auch x2
• Korrelation = 0: Kein linearer
Zusammenhang
Schiefe (1)
• Weiteres „statistisches Moment“ (neben
Mittelwert, Varianz)
• Schiefe ist ungleich 0 wenn Verteilung
nicht symmetrisch
Schiefe (2)
Informationstheorie: Entropie
Datenanalyse: Scatterplots
Hauptkomponentenanalyse